Влияние процессов на стенках капилляра на параметры плазмы положительного столба разряда низкого давления

ПОСТАНОВКА ЗАДАЧИ

Параметры плазмы газовых разрядов низкого давления зависят от процессов взаимодействия молекул, атомов, ионов и электронов плазмы со стенкой разрядной камеры [5], [10]. Твердые поверхности могут служить источниками заряженных частиц за счет электронной эмиссии [11]. На стенках происходит рекомбинация плазменных электронов и ионов, осуществляется теплообмен [16], имеют место различные химические реакции. Характер взаимодействия кроме свойств материала стенки существенно зависит и от степени ее шероховатости [12]. Результаты упомянутых работ носят качественный характер. В данной работе количественно рассмотрено влияние процессов на стенках разрядной камеры на параметры плазмы положительного столба разряда низкого давления и влияние на эти параметры степени шероховатости поверхности стенки.

ЭМИССИЯ ЭЛЕКТРОНОВ

Электронная эмиссия включает в себя эмиссию вторичных электронов, ионно-электронную и фотоэмиссию. Вторичная электронная эмиссия описывается коэффициентом вторичной электронной эмиссии. При малых энергиях налетающих электронов (до 50 эВ) в потоке вторичных электронов преобладают истинно вторичные электроны с коэффициентом эмиссии δ и энергиями порядка 1 эВ и упруго отраженные электроны с коэффициентом эмиссии r и энергиями, равными энергиям налетающих электронов. Величины δ и r для гладкой поверхности зависят от материала стенки и энергии налетающих электронов ε [4]. Зависимость от угла падения слабая.

Поведение δ и r в зависимости от ε имеет довольно сложный характер. Однако, учитывая, что плазменные электроны имеют существенный разброс по скоростям, тонкая структура δ и r не важна. Кроме того, в конечные выражения коэффициенты эмиссии входят под знаком логарифма. Это позволяет для их описания использовать единые аппроксимационные формулы, учитывающие их основные особенности: рост δ начиная с порогового значения εt и наличие максимума у r, равного rm при энергии εm. Таким условиям удовлетворяют выражения:

• 8 = A ( e- e ) a , r = 2,718 r m ^— exp ^J-— L (1)

t                      —m       I 8m J где А, а – постоянные аппроксимации. Используемые нами значения постоянных аппроксимации для диэлектриков, полученные по данным [4], равны: А = 0,18, а = 0,54, εt = 4,5 эВ, εm = 4 эВ, rm= 0,55. Для металлов разброс значений постоянных существенно выше. Поэтому для разрядных камер, собранных из изолированных металлических сегментов, соответствующие коэффициенты аппроксимации даны в таблице.

Коэффициенты аппроксимации

	А	a	εt , эВ	εm , эВ	r m
Си	0,044	0,73	6	10	0,13
W	0,036	0,71	5,5	10	0,2
Al	0,016	0,87	5	4	0,14
Ni	0,012	0,92	4	2.5	0,11

Для расчета средних значений δ и r , получающихся при учете разброса первичных электронов по энергиям и углам падения θ , имеем:

”,,,.__           1

5 = - JJf 5(8,e)dJ₌(u,9) , r = - Jff r ( 8,9 ) dJ_E(u,9) , (2)

J_e 0(2π)                                J _e 0(2π)

где J_e – плотность потока электронов на стенку; dJ_e ( υ , θ ) – плотность потока электронов со скоростями υ в интервале dυ , движущихся к стенке в направлении θ в телесном угле d Ω = sin θ dθ dφ , φ – азимутальный угол. При максвелловской функции распределения электронов (ФРЭ) по скоростям имеем:

dJ e ( и,9) = n e

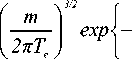
m^— Ц^зо³ di3cos9 dQ , 2T

e

J = n ee

J e ( 1 - P f 5 ) = J i ( 1 + P f Y f ) , Y f = Y + 510 ^{- 2} Q , / в .   (7)

3/2

I I l 2nTe J ’

где m , n e , T e - масса, концентрация и температура электронов, выраженная здесь и ниже в энергетических единицах. Для ФРЭ, отличной от максвелловской, T e - эффективная «температура хвоста» функции распределения -T e' , а перед n e появляется нормировочный множитель X (для газов с высоким потенциалом возбуждения резонансных уровней X ^ 1). Используя выражения (1) по формулам (2), (3), получаем:

5 = A Г (1 + a) 1 + a + — I Tea exp l        ^e J

r = 5,44

У £ 1

rm ε m e

^ + T e ) ³ ’

где Г ( x ) - гамма-функция. Для диэлектриков

имеем:

/

5 = 0,25

l

I                                  I

1 + — I T 0 exp ^|-

T e J        I

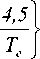
47,8 T r =------ ^e—

(4 + T e )' .

Эффективные коэффициенты вторичной эмиссии с поверхности получаем, домножая выражения (4) или (5) на вероятность вылета частицы без вторичных столкновений P

5 f = P f 5, r f = P f r, о ef = P f о = P f ( 5 + r ) . (6)

Эмиссия электронов при взаимодействии со стенкой ионов для условий разряда носит потенциальный характер, так как энергия ионов не превышает 10³ эВ. В этом случае коэффициенты ион-электронной эмиссии у слабо зависят от энергии налетающих ионов и их можно считать постоянными. Величина у растет с ростом энергии ионизации E a и уменьшается с ростом работы выхода электронов из материала стенки еф. Для оценки у можно использовать эмпирическую формулу [14]: y ~ 0,016 (Е_а - еф ), где Е_а , еф выражены в эВ. Величина квантового выхода фотоэффекта Y растет с ростом энергии фотона hv и имеет тенденцию к насыщению. Для инертных газов hv ~10 эВ и Y ~10^-3 * 10^-1 для различных материалов. С учетом потерь электронов при выходе с шероховатой поверхности имеем: Y f = f ^Y f f = ^P f ^Y ^ ⁵¹⁰" ^P f .

Уравнение баланса зарядов на стенке принимает вид: J. = J e - o ef J e - yJ -Y ff J , где J, J_e , J - плотность потока на стенку ионов, электронов и резонансных фотонов. Учитывая, что J /J. = Q / в , где в - коэффициент ионизации; Q -константа скорости возбуждения резонансных уровней, распадающихся спонтанно [3], и используя (6), получаем:

Плотности потоков на стенку J e и J . равны соответственно:

J e

= n g

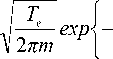
eN I ,       I Te + t

T I ^{, J i} M m

e

= n g

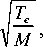
где M - масса атома (иона); n - концентрация заряженных частиц на границе плазма - слой. Используя выражение (7) для падения потенциала в пристеночном слое объемного заряда Лф, получаем:

T

^Ф = —In e I

где T - «температура хвоста» ФРЭ. При максвелловской ФРЭ T e = T e .

КОЭФФИЦИЕНТЫ АККОМОДАЦИИ АТОМОВ И ИОНОВ

Теплообмен тяжелых частиц со стенкой характеризуется коэффициентом аккомодации, равным отношению энергии, передаваемой частицей стенке при столкновении, к максимально возможной энергии. Будем использовать для коэффициентов аккомодации аппроксимационную формулу для однократного рассеяния атомов на решетке твердых сфер [2]: а ₀ = 2,4 ц /(1 + ц )², где ц = M/M w - отношение массы частицы газа к массе атома поверхности.

Реальная поверхность является шероховатой, и поэтому часть атомов после отражения испытывают столкновения со стенкой. Учитывая, что после n -го столкновения со стенкой атом либо покидает ее с энергией E_n=2a₀T w + ( 1 - а ₀) e_n-] , где s n _ 1 - энергия после n - 1 столкновения с вероятностью P_f , либо испытывает еще одно столкновение c вероятностью 1 - P f , для эффективного коэффициента аккомодации атомов получаем:

α а= =----А.

ао + Pf (1 - ао )

Ионы двигаются к стенке в двойном слое объемного заряда по нормали к средней поверхности. Вблизи стенки их траектории несколько искривляются в соответствии с искажением электрического поля вблизи отрицательно заряженной шероховатой поверхности. В отличие от атомов, которые попадают на стенку под всевозможными углами, ионы попадают на стенку под малыми углами 6. Тогда коэффициент аккомодации для такого столкновения равен 1,5 а₀ . Считая, что повторные столкновения описываются коэффициентом аккомодации а₀ , и используя такие же, как и при выводе (9), рассуждения для ионов, получаем:

а₀(1 + 0.5P_f) ai =-----------—.

^ao ^{+ P}f^{(1 - а}о)

Кинетические энергии атомов после столкновения со стенкой s a и после рекомбинации иона на стенке s'a определяются уравнениями:

^Ea = ^2aa^TW + ^{( 1} - ^aa ) ^{2 T}a ’ ^Ea = ^2ai^TW + ^{( 1} - ^ai ) ^E iW , ⁽¹¹⁾

где T w - температура стенки; s_W - кинетическая энергия иона при столкновении со стенкой. Коэффициент 2 в формулах (13) появляется здесь потому, что, в отличие от средней энергии частицы в разряде, равной 3 T /2, средняя энергия, переносимая частицей на поверхность или с поверхности, равна 2 T Величина s iW равна сумме кинетической энергии иона на границе плазма -слой T /2 [16] и энергии, приобретаемой в слое еЛф = А nT e . Тогда для s W получаем:

S iW = 0.5 T_e +^п T e . (12)

ХАРАКТЕРИСТИКИ ШЕРОХОВАТОЙ ПОВЕРХНОСТИ

Будем считать, что поверхность описывается случайной функцией z(x , у) с непрерывными производными z= д z/ д x, z = д z/ 9y, где плоскость ху совпадает со средним уровнем поверхности. Двумерная плотность распределения вероятности случайных величин z 1 , z 2 , соответствующих точкам (x 1 , у), (x₂, y) имеет вид [2]:

f ⁽ z 1 , ^z 2 ) =

2 па \/1 - у²

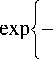
z 1 ² + z 2 - 2 у z 1 z ₂ I

2 a ( 1 — Y ²) J ’

где Y = exp{-t2 /p2} - функция корреляции высот шероховатости; t = (x - x2 )2 + (y1 - у2 )2 - ка жущееся расстояние между точками; о - среднеквадратичное отклонение z от среднего уровня; р - радиус корреляции. При t > р случайные величины z1 и z2 статистически не связаны.

Рассмотрим две близкие точки ( х , у ), ( х + dx , у ) и ( х , у ), ( x + dx , y + dy ). Используя выражение (13), получаем плотности распределения вероятности случайных величин z x и z x , z y :

^fL ⁽ z x ) =

ρ

2 πσ

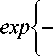
^fS ⁽ zx-z, ) =

ρ2 4πσ2

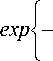
ρ2z

4σ2

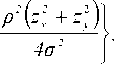
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ШЕРОХОВАТОСТИ

Параметры о и р связаны с непосредственно измеряемыми характеристиками поверхности. В частности, о определяется классом точности обработки поверхности, а р можно связать с отношением истинной площади поверхности с кажущейся ^ S , или отношением истинного расстояния на поверхности к кажущемуся ^ L , которое определяется по профилограмме.

Очевидно, что ^_s и ^ L равны соответственно математическому ожиданию величин dS / dxdy и dl / dx , где dS и dl - элементы площади и длины на поверхности, соответствующие элементам dxdy и dx в плоскости xy . Учитывая, что dS / dxdy = 1 + z x + z 2 , dl / dx = V1 + z x для ^ S и ^ L , имеем:

+M+M ___________ +К ______

^ s = J J V¹ + x X + z y ^{f (} z z y ^dxdy , ^ L = J V^{1 +} 4 ^fL ⁽ z x ) ^d x . -К-M                                   -К

Используя формулы (14) для f_S , f L и аппроксимируя результаты интегрирования, получаем:

V s = V 1 + nP S , ¥ l = ^ 1 + 4P S /n ,     (15)

где P s = о/р - параметр шероховатости реальной поверхности. Эти же параметры можно определить независимо по рассеянию лазерного излучения поверхностью [9].

ВЕРОЯТНОСТЬ ВЫЛЕТА ЧАСТИЦЫ С ШЕРОХОВАТОЙ ПОВЕРХНОСТИ БЕЗ СТОЛКНОВЕНИЙ

Электроны, эмитируемые стенкой, атомы после столкновения со стенкой и атомы, образовавшиеся при рекомбинации ионов, могут испытывать повторные столкновения. При этом коэффициент эмиссии электронов уменьшается, а коэффициент аккомодации атомов растет. Учесть это явление можно, вводя вероятность вылета частицы с шероховатой поверхности без столкновений P_f . Для расчета P_f определим среднеквадратичный тангенс угла наклона поверхности. Используя формулу (14) для f_L , получаем: zz^ = J z x f_L ( z_x ) dz x = 2 P _s ². Тогда средний угол наклона поверхности относительно плоскости xy 9_f будет приблизительно равен:

O f = arctg^z x = arctgP_s .         (16)

Пусть ф - угол рассеяния частицы поверхностью, отсчитываемый от среднего уровня. Считая, что все направления в пределах от 0 до п /2 равновероятны, для вероятности рассеяния частицы в пределах dф имеем dP = 2 dф/п. Введем вероятность вылета частицы под углом ср без повторных столкновений P(ф ). Очевидно, P ( ф ) = 0 при 0 <  ф < 9_f и P ( ф ) = 1 при 9_f <  ф < п /2. Тогда вероятность вылета частицы с поверхности без столкновений будет равна:

п /2                21

Pf = J P(^)dPT = -arctgYTn?,(17)

0          п2V где для 9f использована формула (16). На рис. 1 приведена зависимость Pf от Ps, рассчитанная по формуле (17), в сравнении с экспериментальными данными по вероятности вылета электронов с шероховатой поверхности для различных материалов с различной степенью шероховатости [4].

Зависимости P_f от материала не прослеживается. Соответствующие значения, приведенные на рис. 1, определены путем обработки профилограмм поверхностей, полученных с помощью электронного микроскопа с использованием формулы (15) для Ψ_L .

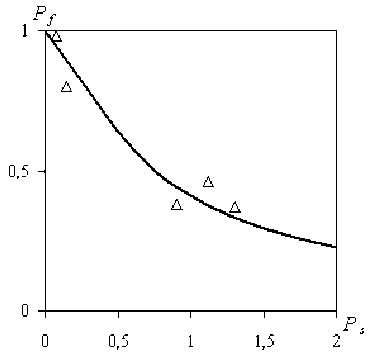
Рис. 1. Зависимость P _f от параметра шероховатости P_s ; Δ – эксперимент; ( ^__ ) – расчет по формуле (17)

УРАВНЕНИЕ РАВНОВЕСИЯ ПЛАЗМЫ И ТЕМПЕРАТУРА ИОНОВ

Теория квазинейтрального положительного столба разряда низкого давления в продольном магнитном поле с индукцией B в режиме, когда длина свободного пробега ионов сравнима с радиусом капилляра, развита в работе [18]. Уравнение равновесия плазмы, выражающее баланс заряженных частиц, имеет вид:

n a ^в =

^S g ⁽ 5 ) / T e + T

R M ^,

где T_i – температура ионов; S_g –

безразмерная параметра δ :

эффективная

граница плазмы, зависящая от

m  ω_e ²

δ=^{Q ia} +

4β 2M n a βv e

v = n Q + n Q — e a ea e ei

частота столкновений электронов с атомами и ионами; Q_ea , Q_ei , Q_ia – транспортные константы скоростей столкновений электронов с атомами и ионами и ионов с атомами; го = eB / m - электронная гирочастота; чертой здесь и ниже обозначается усреднение по сечению разряда. Аппроксимируя результаты [18] для S_g , получаем: S_g = 1,092(1 + 0,142 δ )^–1/2. Когда длина свободного пробега ионов λ_i<< R (режим амбиполярной диффузии, δ велико), уравнение равновесия (18) соответствует результатам теории Шоттки. В случае λ_i >> R при отсутствии магнитного поля ( δ = 0) уравнение (18) совпадает с уравнением равновесия плазмы Тонкса – Ленгмюра.

ФР ионов по скоростям в разрядах низкого давления существенно анизотропна. Продольная температура ионов TII близка к температуре атомов, а поперечная T существенно превышает Ta, что связано с высокой радиальной скоростью ионов, которая на границе плазмы и пристеночного слоя объемного заряда достигает величины Te/M . В случае свободного падения ионов на стенку: T┴ = 0,56Ta + 0,13Te [6], или T┴ = 0,64Ta + 0,118Te [6]. В общем случае (X. ~ R); используя распределение радиальных скоростей ионов [18] и метод, аналогичный изложенному в [6], получаем аппроксимационную формулу для T┴:

T _L = [ 7 - 0.348² 2 ( 5 ) ] T + 0.0948² 2 ( 5 ) T , (19)

которая при X i >>  R согласуется с результатами [6], [7], а при X. <<  R дает T = T a . Эффективная температура ионов равна: T _┴ ≅ T_a .

T =( T „+2 T _L )/3. ° (20)

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ И КОНСТАНТЫ СКОРОСТЕЙ

ПРОЦЕССОВ

На практике используют разряды двух типов: слаботочные тлеющие, где концентрации электронов n_e ~ 10⁹–10¹¹ см^-3, и сильноточные с накаленным катодом, где n_e ~ 10¹³–10¹⁴ см^-3. В последнем случае вследствие интенсивных межэлектронных столкновений ФРЭ близка к максвелловской, тогда как в слаботочных разрядах она «на хвосте» обеднена из-за процессов возбуждения, ионизации и ухода быстрых электронов на стенку. Кроме того, длина релаксации ФР по энергии сравнима с R , что приводит к не-локальности ФРЭ [17].

При расчете нелокальной ФРЭ в кинетическом уравнении (КУ) необходимо сохранить члены, описывающие поперечную неоднородность плазмы [17]. Каждый акт ионизации сопровождается уходом одного быстрого электрона на стенку, и эти процессы разделены в пространстве. Для приближенного учета явления нелокальности заменим поперечные члены в КУ, описывающие радиальное движение электронов, добавкой в интеграле столкновений к частоте неупругих столкновений v_in частоты ухода быстрых электронов на стенку v _w, равной частоте ионизации v_i . Таким образом, вместо v_in = v_ex + v_i , где v_ex – частота возбуждения, используем v'_in = v_ex + 2 v_i . При этом изотропная часть ФРЭ, полученная по методу [3], ведет к изменению константы скорости возбуждения и коэффициента ионизации на фактор F, а температуры «хвоста» ФР T_e , на фактор D :

Q = Q ( T e ) F , в = в Г е ) F , T e = T e D ,         (21)

где

_F = 1 У1 +4 С - 1 _D =      2        _C = v n = n_a [ S ex, ( T e ) + 2 в ( T_e )]

C 1 + 4 C + 1 ,       V1 + 4 C + 1 ,       v ee             v ee         ’

Q(Te), β(Te) – соответствующие константы при максвелловской функции распределения с эф- фективной температуры Te; ve - частота меж электронных столкновений с энергией, превышающей пороговую для возбуждения.

ЗАКОН ОМА И БАЛАНС ДАВЛЕНИЯ

Для сильноточного разряда необходимо учитывать торможение электронной компоненты при упругих столкновениях с ионами и вытеснение нейтрального газа электронами и ионами.

j = eEz      ne m n Q + n Q a ea e ei

P = n a T a ⁺ n e ( ^T e ⁺ T ) ,

где j , p - средняя по сечению плотность тока и давление наполнения; Е - напряженность продольного электрического поля. В слаботочном разряде можно положить n e = 0. В уравнении баланса давления пренебрегалось небольшим нетепловым вытеснением нейтрального газа из капилляра вследствие явления электрофореза и температурной транспирации. В сильноточных разрядах электрофорез компенсируется с помощью обводного канала, соединяющего катодный и анодный узлы разрядной трубки.

ТЕМПЕРАТУРА АТОМОВ И БАЛАНС ЭНЕРГИИ

В РАЗРЯДЕ

В слаботочных разрядах температура атомов соответствует температуре стенки. В сильноточных разрядах температура атомов достигает нескольких тысяч градусов Кельвина. Уравнение баланса энергии атомов запишем в интегральной форме:

^2nRJ a Х T — ^T w ) = ^nR\n a

1Q..3 ( T - T ) + ₂ ia ₂ i a

⁺ T7 ^Q ea "^e — ^T a ^{) + в} f ^Е « — "^^Ta ^ , M2     (   2 )

где J a = n a V T a /2 п M - плотность потока атомов на стенку. Левая часть данного уравнения описывает теплообмен атомов со стенкой, первый и второй члены правой части - обмен при столкновениях с ионами и электронами, третий член учитывает, что каждый акт ионизации ведет к появлению атома на стенке с энергией s'a и к «исчезновению» атома в разряде с энергией 3 T a /2.

T a = ^T W ⁺ — n e i 1ПГ ^{2 a} i ^T W ^{+ (1} - “ i ^)s iW — T ^T a =

« а П а \^T a L                       2 J

• ⁵ T w + s "  e .            (23)

Па \ 8Ta «a и T >> TW

Уравнение баланса

В слаботочных разрядах n e /n a ~10 " ⁷-10 " ⁶ и T a e T_W В сильноточных разрядах n_e /n_a ~10^-2-10^-1 энергии в разряде в интегральной форме имеет вид:

^{nR 2 j} E_z = ^{2 n R} ' J , . ^[ E a + a ⁽ е _да ^- 2T W ) -P f Ye , ^]+

^{+ J} e ^{[ 2T} e - ^P f ⁽ r^e r ^{+ 5e} s ^{) ] +}

+ J a 2 a ( T a - T w ) + J , ( E , - 510 ^{- 2} P f p ) } , где E - энергия резонансных фотонов; s_r = 2 Te , £& ~ ^В, ^S y = ^{0,5( E} a ^- e Ф )’ S = ^{0,5( Е} _Ф ^- e Ф ) ^- средние кинетические энергии вторичных электронов: упруго отраженных, истинно вторичных, образующихся при ион-электронной эмиссии и при фотоэффекте. Используя выражения для плотностей потоков частиц на стенку и формулу (23), получаем:

s„ Tз_ jEz =           Pa + 'w —5 Ta—Pf Ye, +

R V M a I

+ 1 + Pf Yf [2T — p (re + ge )] + Q^ (e - 510-5 Pf e )|. (24) e f r °               V

• 1    - Pf ap

АПРОБАЦИЯ РЕЗУЛЬТАТОВ

Анализ системы уравнений (18, 19, 20, 22, 23, 24) показывает, что для разрядов низкого давления справедлив приближенный закон подобия, согласно которому при R -преобразовании внутренние инварианты n e R , n a R , T e , T a , T, ER остаются неизменными, если сохраняются внешние инварианты p , jR , BR , а также материал стенки и технология его обработки.

Отклонение от закона подобия связано с зависимостью коэффициента ступенчатой ионизации от концентрации электронов, а не от произведения n R . Наиболее ярко зависимость внутренних параметров плазмы от свойств материала стенки и степени ее шероховатости P s проявляется для сильноточных разрядов.

На рис. 2 представлены зависимости n_eR и T_e от a a и o ef , а также от связанного с ними параметра шероховатости R s для разряда в капилляре из бериллиевой керамики ( a 0 = 0,44, у =0,17, для охлаждаемой стенки T_W s 320 K =0,027 эВ). При расчетах использовались данные о сечениях процессов, собранные в [13], а при расчете коэффициентов прямой и ступенчатой ионизации e r , P t , , ( в_г = в_г + e st ), и констант скоростей Q_ex , Q - методика [3]. С ростом P s или а величина T уменьшается, а n_eR растет. Рто обусловлено ростом эффективности теплообмена со стенкой, уменьшением атомной температуры и увеличением концентрации атомов в разряде. При этом температура электронов должна уменьшаться, а для поддержания неизменности тока разряда их концентрация должна возрасти.

С ростом степени шероховатости будет одновременно изменяться величина o_ef Однако предыдущий вывод остается в силе, так как коэффициент вторичной электронной эмиссии в силу ухудшения условий выхода электронов с поверхности будет уменьшаться, а, как показано на рис. 2б, параметры T e и nR при этом имеют тенденцию к насыщению. Одновременно существенно расширяется область стабильного горения

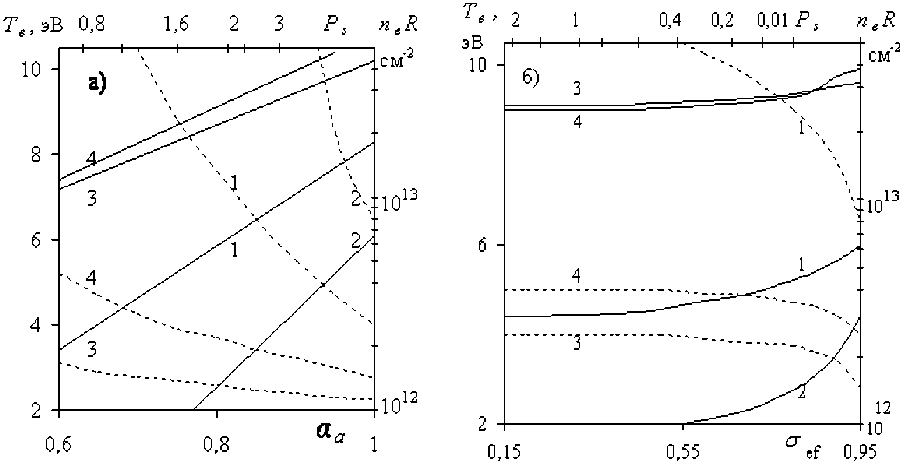
Рис. 2. Зависимости Т_е (---) и nR (___) от a a при o f = 0,8 (а) и от o f при a a =0,9 (б); pR = 0,06 Торсм,

* jR = 50 Асм^-1 (1), 100 (2); pR = 0,2, jR = 50 (3), 100 (4)

разряда по току, так как обрыв разряда, обусловленный вытеснением нейтрального газа из капилляра, происходит при больших токах [8].

При данных значениях pR и BR величина nR с ростом jR уменьшается вследствие разогрева нейтрального газа и его вытеснения электронами, а электронная температура растет. Это приводит при некотором критическом значении (jR ) cr к нарушению равновесия между частотой ухода ионов на стенку, неограниченно растущей с ростом электронной температуры

Vw = ( SgjR W+t№ , и частотой ионизации n j e, ограниченной в силу уменьшения n_aR и насыщения в , и к обрыву разряда. Для расчета (jR ) cr необходимо к рассмотренной системе уравнений добавить условие (djR/ 9 T ) R _BR = 0 . На рис. 3 представлены зависимости nR от jR и (jR ) cr от pR в сравнении с экспериментальными данными.

Отметим, что вблизи обрыва разряда возбуждаются плазменные неустойчивости [8], [1], что, по-видимому, приводит к превышению расчетных значений над данными эксперимента.

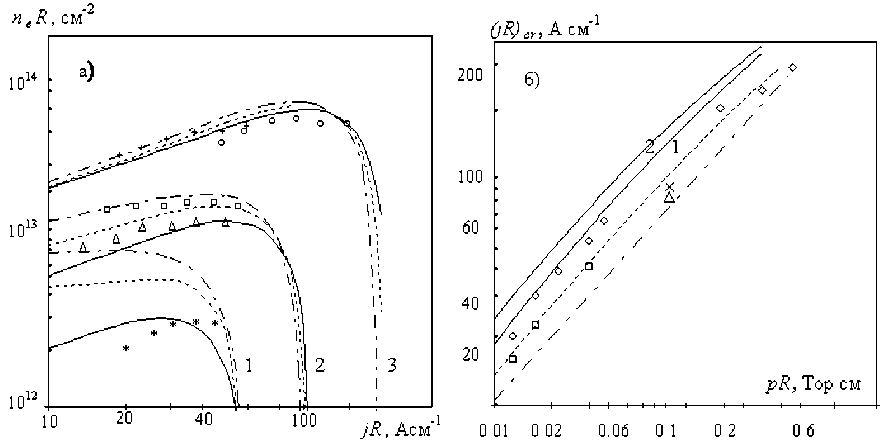
Рис. 3. Зависимости nR от jR (а) при pR = 0,03 Тор см (1), 0,1(2), 0,4 (3); (—) BR = 0, (—) - 10^-2 Тсм^-1 , (-■-■-■) - 2 • 10^-2; эксперимент: * - pR = 0,03 Тор см, Br = 0; + - 0,4,0; □ - 0,11, 0; ° - 0,38, 0; А - 0,06, 0 [10]. Зависимости (jR) от pR (б) при P = 3 (1), BR = 0,10^-2 Тсм, 2 • 10^-2; при P = 4, BR = 0 (2). Эксперимент: ° - BR = 0; □ - BR = 0,6 • 10^-2 Тсм;

¹                  х - BR = 1,5 • 10^-2 Тсм [8]; А - BR = 1,7 • 10^-2 Тсм; ◊ - BR = 0 [1]

ЗАКЛЮЧЕНИЕ

Из приведенных данных следует однозначный вывод: при расчетах параметров плазмы разрядов низкого давления необходимо учитывать процессы на стенках разрядного капилляра. Отметим, что аналогичные явления имеют место в многочисленных исследованиях последнего времени, касающихся пылевой плазмы [15]. Так, при расчете зарядки пылевых частиц необ- ходимо учитывать эмиссию вторичных электронов, ион-электронную и фотоэмиссию. Кроме того, разогрев пылевых частиц при бомбардировке их ионами и последующей рекомбинации с электронами приводит к термоэмиссии электронов. При теоретическом анализе этих процессов также могут быть использованы полученные в данной работе результаты для коэффициентов эмиссии.