Влияние пространственной корреляции дефектов на рассеяние рентгеновских лучей от полупроводниковой сверхрешетки

Известно, что интенсивность диффузного рассеяния рентгеновских лучей (РЛ) от сверхрешетки (СР) распределяется вокруг основного брэгговского пика и дифракционных сателлитов [1]. Теоретически данное физическое явление исследовано для модели гармонической СР [2]. Отмечено, что причиной такого поведения диффузного рассеяния является корреляция хаотически распределенных по объему СР структурных дефектов. В случае полупроводниковой сверхрешетки, когда период состоит из тонких слоев разного композиционного состава, теоретически обосновать формирование диффузного рассеяния вокруг сателлитных дифракционных порядков оказалось достаточно сложно [3]. Возникновение сателлитных диффузных пиков от полупроводниковой СР возможно лишь в случае, если структурные дефекты в разных слоях имеют пространственную корреляцию, что ранее не исследовалось. До этого корреляционные эффекты, вызванные структурными дефектами, учитывались только внутри отдельного слоя сверхрешетки [4].

С другой стороны, многочисленные экспериментальные результаты и теоретические разработки (см. [5] и приведенную в ней литературу) показывают, что при различных технологических процессах создания многослойных структур верхние слои, как правило, наследуют структурные особенности нижних слоев. Это относится, например, корреляции межслойных шероховатостей в процессе формирования многослойных структур [6], морфо- логическим изменениям гетерограниц [7], периодическому распределению точечных дефектов [8] и пространственному распределению квантовых точек [9] в полупроводниковых СР.

Настоящая работа посвящена разработке теории когерентного и диффузного рассеяния от полупроводниковой СР применительно к высокоразрешающей трехкристалльной дифрактометрии. Используя формализм [10] для амплитудного коэффициента когерентного рассеяния от N-периодной СР получаем

R^c ( q, , q z ) = iF s ( q z ) e‘* ^S1 " ⁽ Ny ) W ( q x ) , ^{(1) sin(} y )

где y = A I 1 + A 2 I 2 , A 12 = ^{( (} ba ₀ ^- q_z ) + £_VTh ) /2 , / = ( N - 1) y + A 1 1 1 . Структурная амплитуда сверхрешетки имеет вид

F s ( q z ) = a , f ^^in^ + e ’ a 2 f . ^S1"‘ ' ' l ⁾ . (2)

A 1 A 2

Здесь a 1,2 – рассеивающие способности первого (верхнего) и второго слоев периода СР, f 1,2 – статические факторы Дебая-Валлера, 1₁₂ - толщины, d 1,2 – межплоскостные расстояния отражающих атомных плоскостей этих слоев. Величины £ 1 = А d 1 / d , e ₂ = А d ₂ / d определяют рассогласование межплоскостных расстояний слоев СР относительно подложки d , где А d 1 = d 1 - d и А d ₂ = d ₂ - d . Определим d_SL = ( d 1 1 1 + d ₂ 1 ₂ )/ 1

как среднее межплоскостное расстояние сверхпериода, тогда

S SL = ( d_SL - d ) / d = ( s 1 1 1 + s ₂ 1 ₂) / 1       (3)

– деформация среднего межплоскостного расстояния СР относительно подложки. Эта величина определяет угловое положение основного (нулевого) пика СР относительно брэгговского угла θ_B подложки:

® sl = ^{- tan(} 6 B ^{) s}sl .

Если не брать во внимание появление в (1) функции

L x

W (Qx )= J dx exP(iQxx)- где Lx – ширина засветки для ограниченной в латеральном направлении падающей рентгеновской волны, то решение (1) по своему виду совпадает с ранее полученным результатом для идеальной [11] и искаженной [4] сверхрешетки.

Более детальному анализу подлежит диффузное рассеяние рентгеновских лучей от случайных структурных нарушений СР. Будем исходить из общего решения [10] с учетом усреднения интенсивности рассеяния вдоль направления, перпендикулярного плоскости дифракции.

Диффузное рассеяние от нарушенного кристаллического слоя зависит от фазового фактора ф (x , z ) = exp ( i hu ( x , z ) ) , который запишем в виде суммы ф ( x , z ) = ф (x , z ) + 5ф ( x , z ) , где первое слагаемое ф ( x , z ) = exp ( / h u ( x , z )) ) - описывает неслучайные крупномасштабные деформации в нарушенном кристаллическом слое. Хаотические атомные смещения, вызванные, например, распределенными в этом слое дефектами, задаются случайной фазовой функцией ф ( x , z ) = exp ( i h S u ( x , z ) ) , при этом f ( x , z) = ф ( x , z )^ - статический фактор Де-бая-Валлера.

Пренебрегая первичной и вторичной экстинкцией короткопериодной СР, запишем выражение для интенсивности диффузного рассеяния

L z L x

I d ⁽ Q x , Q z ) = J ^dz J ^dx\ah\ ^{2(1 -} f² M ^x , ^z ; Q x , Q z ) . ⁽⁴⁾ 0     0

Здесь

+to +to

^{m ( x} , ^z ; q x , Q z ) ^ -ⁿ ) J ^d P x J d P z ^ex P ^{( i} [ Q x P x ⁺ Q z P z ^{] )x} (5) -to -to

Ф *⁽ x ⁺ P x , ^{z +} P z^{) ф ( x} , ^z ) G ^{( x} , ^z ; P x ^,0, P z )

– площадь корреляции. Тип дефектов описывается корреляционной функцией

G ⁽ x , z ; P x ^,0, P z ) =

• < exp ( i h [ S u ( x + P _x , z + P z ) - S u ( x , z ) ] ) > - f ²( x , z ) . (6)

словами, диффузное рассеяние возникает из-за наличия дефектов в определенном пространстве периода СР, например, в нарушенном слое толщиной I D <  l , причем это пространство не обязательно связано с границами слоев периода. Такие характерные нарушения периодически повторяются по всей толщине сверхрешетки.

Средняя деформация решетки периодически расположенных нарушенных слоев sSl = (S1 ID + S 212D )/ID                 (7)

может отличаться от средней деформации СР ε _SL , где l 1D ₂ - толщины нарушенных участков в слоях периода СР, I D = I D + 1 D .

Фазовая функция крупномасштабных искажений ф(x,z) представлена в виде произведения: ф(x, z) = фSL (x, z^)фь (x, z), при этом первый сомножитель фSL (x,z) описывает периодические деформации в вертикальном направлении фSL (x, z +1) = фSL (x, z) и зависит от средней при-D веденной деформации εSL для нарушенного слоя отдельного периода СР. Второй сомножитель фL (x,z) описывает деформации СР в латеральном направлении.

Если в горизонтальном направлении СР однородна, т.е. отсутствует латеральная модуляция композиционного состава, то ф _L ( x , z ) = 1 . С другой стороны, если один из слоев СР содержит спонтанно организованные наноструктуры в виде квантовых нитей или квантовых точек, то ф _L ( x , z ) описывает пространственную корреляцию нанообъектов (ближний или дальний порядок их расположения).

При наличии строгой вертикальной модуляции композиционного состава ф _SL ( x , z ) = ф _SL ( z ) является периодической функцией вдоль направления z , поэтому ее можно разложить в ряд Фурье:

to

• ^ SL ( z ) = E ^Bn ^eX P ^{( in K} z z ) ,             ⁽⁸⁾

n=-to где Kz = 2n /1 - период модуляции сверхрешетки в обратном пространстве (расстояние между дифракционными сателлитами). Учитывая, что в выражении для коррелятора быстро осциллирующими членами можно пренебречь, получаем to

Ф к ^{( z +} P z Xl ^{( x} , ^z ) ~ E B n 1^{2 eX}P ^(- in ^K z P z ) .

n =-to

Фурье-коэффициенты находятся вычислением ин-

• 1    ¹

теграла B n = _J ф_sL ( z )exp ( - in K z ) dz .

• ¹ 0

Учет латерального распределения дефектов приводит к следующему выражению для корреляционной площади to

^{z (}Q x , Q z ) = ^{L (} Q x ) E B n 1^{2 f} n ⁽ Q x , Q z ) .         ⁽⁹⁾

n =-to

Здесь этот параметр записан в виде суммы локальных корреляционных площадей соответствующих дифракционных порядков n = 0, ±1,±2,...

1 +to +to

T ⁽ q x , q z ) = 2- J d p x J d p z

X

-to

-to

exp i q x P x ^{+ (} q z ^- n ^K z ^- h e D ) P G L_L ( P x ^,0, P z )

где Gsl(px,0, pz) - корреляционная функция де- фектов в нарушенном слое периода СР.

Стоящий в выражении (6) перед суммой сомножитель

^ +to                                   ^

L(qx) = J cl (Px)dPx exp(iqxPx) у-»                        J определяется через корреляционную функцию

CL (Px) = ф^ (x + Px )фL (x) и характеризует про- странственную упорядоченность в распределении дефектов в латеральном направлении. Если в нарушенном слое М дефектов, то в рамках дискретного распределения [12]

L ( 4 x ) = 1 +

2 Re fZ (qx)((1 -Z (qx» M - (' -Z (qx' M)))

M Ц           (1 - Z ( q x ))²           JJ

где ^{Z (} q x ) = ^{f (} q x WO q x T ) . f ( q x ) = W iq x S T )) – эффективный фактор латерального порядка.

Здесь T = T + 5 T - расстояние между соседними дефектами, δ T – случайные отклонения от среднего значения T . Влияние пространственной (латеральной) корреляции на диффузное рассеяние от латеральных неоднородностей детально исследовано в [12-14].

Решение для углового распределения диффузного рассеяния от сверхрешетки имеет вид I d ⁽ q x , q z )=| ^aD |^{2 (1 - f}D ²) ^{T (} q x , q z ) ^Lz ^Lx .    ⁽¹²⁾

где a D = ( a 1 I D + a 2 1 2D )/ l_D - рассеивающая способность и f_D = ( f 1 I D + f 2 1 D )/ l_D - средний статический фактор Дебая-Валлера нарушенного слоя в структуре периода СР.

Если сверхрешетка в латеральном направлении однородна и отсутствуют корреляционные эффекты между слоями СР, то в (5), с учетом фSL (x, z) = exp(/he,z) для первого слоя с де формацией e = Ad 1 / d и второго с e 2 = Ad2 / d , получаем ф *(x + Px, z + Pz) Ф(x, z) = exp(ihe^Pz).

В результате площадь корреляции периода СР представима в виде суммы для верхнего и нижнего слоев т (x, z; qx, qz) = T1 (x, z; qx, qz)+T 2 (x, z; qx, qz), где

+to      +to

^T 1,2 ^{( x} , z ; q x , q z ) = ^{( 1} / ^{2 n} ) J ^dP x J ^dP z ^X

-to     -to

exp ^{( i} [ q x P x ^{+ (} q z ^{+ h e} 1,2 ) P z ^{] ) G} 1,2 ^{( x} , z ; P x ,^0, P z ^{) .}

Здесь G ₁₂ ( x, z ; P _x ,0, P _z ) - корреляционные функции дефектов первого и второго слоев периода СР. Интенсивность диффузного рассеяния от одного периода СР, например с номером n, запишется в виде

L x	f,2/                               ^ J dza 1 ( 1 - f Ы x, z q x , q z ) +
I d ( q x , q z ) = J dx ^ 0	0 1 2 J dza 2 2 ( 1 - f 2 )^2 ( x , z q x , q z ) у 0                                J	(14)

По своей структуре выражение (14) совпадает с соответствующим решением для двухкристалль-ной дифрактометрии [4]. Поскольку рентгеновские кванты, проходя каждый период СР, испытывают фотопоглощение, то диффузное рассеяние от сверхрешетки, состоящей из N периодов, примет вид

N

I d ⁽ q x , q z ) ^ £ I d ⁽ q x , q z ^{) e}xp^{( -} p ^{1 [} n ^{- 1])}.     ⁽¹⁵⁾

n = 1

В этом выражении p = ( р 1 1 1 + p₂1 ₂ )/ 1 -средний коэффициент поглощения периода СР, где p 1 ₂ - коэффициенты поглощения рентгеновских лучей первого и второго слоев периода СР, соответственно.

Численное моделирование карт и сечений распределения интенсивностей рассеяния от сверхрешетки проведено на основе решений (1) и (12), (15). Использовались параметры, соответствующие (004) – отражению перпендикулярно поляризованного CuK α – излучения [15]. Модель сверхрешетки состояла из подложки GaAs, на которой находилась многослойная десятипериодная структура InGaAs/GaAs. Толщина слоя InGaAs составляла 40 nm, слоя GaAs – 60. Средняя относительная деформация решетки СР относительно подложки e _SL = 1.4 x 10 ^{- 3} , что соответствовало угловому сдвигу в обратном пространстве A q^⁰ = - 0.064 nm ^{- 1} . Статический фактор Дебая-Валлера первого слоя периода СР GaAs f, = 0.7 , второго слоя InGaAs f ₂ = 0.5 . Дифракция рентгеновских лучей от подложки вычислялась на основе уравнений динамической теории рассеяния.

Сначала рассмотрим случай, когда отсутствует корреляция структурных нарушений между слоями СР. Размеры блоков мозаики в вертикальном направлении для InGaAs соответствовали толщине слоя, для GaAs – половине толщины слоя. В латеральном направлении в обоих слоях корреляционные длины были равны 80 nm. На рис. 1 показаны q z -сечения когерентного, диффузного и полного рассеяния рентгеновских лучей (рис.1а), а также карты когерентного (рис.1b) и полного (рис.1с) рассеяния в обратном пространстве. В отсутствии межслойной корреляции дефектов формируются два пика диффузного рассеяния при значениях q z^GaA^s ) = 0 и q z^InGaAs ) = - 160 pm ^{- 1} . Эти угловые положения соответствуют деформациям в слоях сверхрешетки.

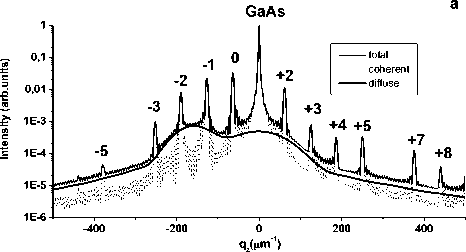
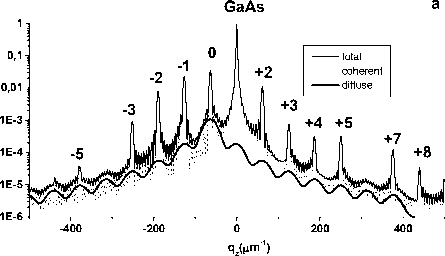
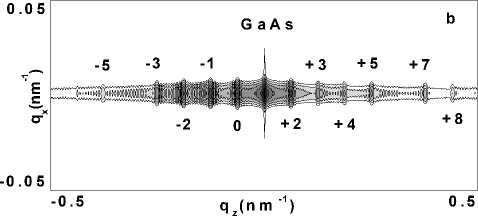
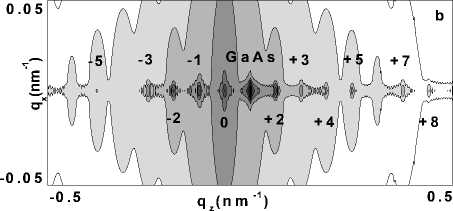
Рис. 2. Дифракция рентгеновских лучей на InGaAs/ GaAs сверхрешетке при наличии межслойной корреляции однородно распределенных дефектов.

а – расчетные q z -сечения когерентной, диффузной и полной интенсивности рассеяния сверхрешетки; b – карта распределения интенсивности когерентного и диффузного рассеяния от СР вблизи узла (004) обратной решетки .

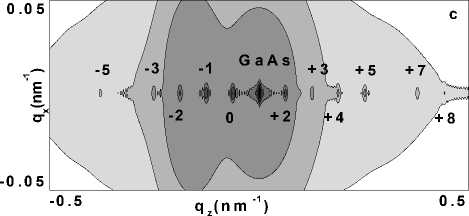
Рис. 1. Дифракция рентгеновских лучей на InGaAs/ GaAs сверхрешетке в отсутствии межслойной корреляции дефектов.

а – расчетные q z -сечения когерентной, диффузной и полной интенсивности рассеяния от сверхрешетки; b – карта распределения интенсивности когерентного рассеяния от СР вблизи узла (004) обратной решетки; с – карта распределения интенсивности полного (когерентного и диффузного) рассеяния от СР вблизи узла (004) обратной решетки.

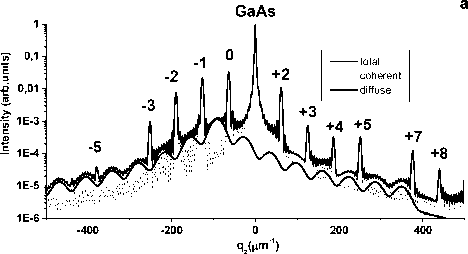
В случае, когда корреляция дефектов выходит за пределы отдельного слоя, диффузное рассеяние имеет осцилляционную структуру с периодом q ZSL ) = 63 p m - 1 (рис.2). Для однородно распределенных дефектов максимумы диффузного рассеяния совпадают с пиками когерентного рассеяния.

Если дефекты, например, в GaAs преимущественно сосредоточены только на одной половине толщины слоя, при этом вторая половина имеет идеальную кристаллическую решетку, максимумы диффузного рассеяния сдвигаются в сторону меньших углов (рис.3). Следует отметить, что период осцилляций диффузной компоненты при этом не изменяется. Этому эффекту можно дать следующее объяснение. Выход диффузного рассеяния осуще-

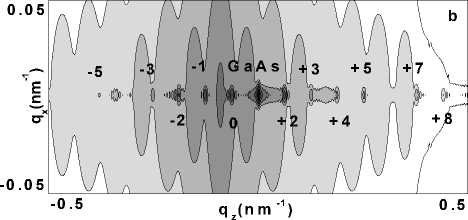
Рис. 3. Дифракция рентгеновских лучей на InGaAs/ GaAs сверхрешетке при наличии межслойной корреляции неоднородно распределенных дефектов.

а – расчетные q z – сечения когерентной, диффузной и полной интенсивности рассеяния сверхрешетки; b – карта распределения интенсивности когерентного и диффузного рассеяния от СР вблизи узла (004) обратной решетки.

ствляется полностью из слоя InGaAs и частично из слоя GaAs, поскольку вторая половина этого слоя дефектов не содержит. Так как периодическая структура для некогерентного рассеяния в вертикальном направлении сохраняется, при этом изменяется только толщина, с которой выходит диффузное рассеяние, а период остается прежним, расстояния между максимумами диффузного рассеяния такое же, как для однородного распределения дефектов (рис. 2, 3). Согласно (7), средняя деформация «дефектной сверхрешетки» e SL = ( s , 1 D + s 2 1 2D )/ 1_D = ( s , 1 1 /2 + e ₂ 1 ₂)/( 1 1 /2 + 1 2 ) = 2 - 10 - 3 .

Нулевой максимум диффузного рассеяния в этом случае сдвинут на ^q\ diff) =- 0.091 nm - , а осцилляции диффузной компоненты приблизительно находятся между когерентными пиками (рис.3).

Таким образом, максимумы интенсивности диффузного рассеяния от СР могут быть сдвинуты относительно когерентных пиков, при этом среднее межплоскостное расстояние когерентной сверхрешетки может отличаться от такого же среднего параметра СР, сформированной из участков, содержащих структурные дефекты.

Работа выполнена при финансовой поддержке РФФИ (грант № 07-02-00090-а) и Программы развития вычислительных, телекоммуникационных и информационных ресурсов УрО РАН - РЦП-2009 (проект П2).