Влияние пузырьков газа на вибрационные параметры измерительных трубок кориолисового расходомера

Кориолисовы расходомеры (КМР) за три десятилетия, прошедших с момента их массового появления на рынке, получили широкое распространение в самых разных отраслях промышленности и заслужили признание благодаря точности и надежности измерений массовых расходов и плотностей однородных, однофазных флюидов. История создания этих устройств и основные этапы в развитии их теории и практического применения подробно описаны в обзорах [1–4], краткий обзор современных исследований приведен в работе [5]. Для однофазных потоков теория измерений разработана достаточно глубоко для того, чтобы предсказывать рабочие характеристики КМР данной конструкции или проектировать приборы с заданными характеристиками [6].

Успехи в применении КМР к однофазным потокам постоянно стимулируют попытки распространить метод и на многофазные потоки. Возникающие в этом случае задачи весьма разнообразны и сильно различаются по сложности в зависимости от количества фаз, их физических свойств и списка характеристик потока, подлежащих измерению. Очевидно, что не все из этих задач могут быть решены «неинвазивно», так, как это делается в однофазном случае – по наблюдениям за движениями трубопровода, возбуждаемыми потоком флюида. Наиболее простым является случай двухфазного потока, в котором одна из фаз является мелкодисперсной и равномерно распределенной по объему трубопровода. В этом случае флюид можно рассматривать как гомогенную жидкость с некоторым эффективным набором свойств [7] и для измерения его массового расхода использовать те же средства, что и для однофазных потоков. Примером являются потоки «жидкость–газ» при достаточно большой приведенной скорости жидкости, когда газ присутствует в потоке в виде мелких пузырьков (режим дисперсных пузырьков [8]). Как показывает практика, «однофазный» подход остается достаточно точным, если объемная доля газа не превышает нескольких процентов. Дальнейшее ее увеличение приводит к неприемлемой потере точ- ности и надежности измерений. Причиной является образование крупных газовых пузырей с размерами, сопоставимыми с диаметром трубы, – переход от пузырькового режима течения к т. н. снарядному (пробковому) режиму, в котором модель гомогенного флюида перестает работать. Качественно понятно, почему в этом режиме нарушается работоспособность КМР: распределение массы флюида вдоль измерительной трубки становится существенно неоднородным и изменяющимся во времени случайным образом, что ведет к случайным же изменениям наблюдаемых параметров колебаний – основной частоты колебаний трубки и фазового сдвига между колебаниями ее плеч. В настоящее время предложен эмпирический метод решения этой задачи, позволяющий получать надежные результаты для потоков, где объемная доля газовой фазы достигает 80 % [9–11]. В то же время отмечается, что дальнейшее совершенствование метода требует более глубокого понимания механизмов взаимодействия двухфазного флюида с измерительной трубкой КМР и разработки соответствующих физических моделей, позволяющих предсказывать отклик прибора на двухфазный поток.

В настоящем сообщении приводятся результаты экспериментальных исследований отклика КМР на возмущения, вносимые короткими пакетами газовых пузырей, импульсно инжектируемыми в однородный поток жидкости. Описываются результаты численных экспериментов, полученные с помощью конечноэлементной модели прямой измерительной трубки КМР, в которой поток описывается в 1D-приближении и характеризуется неоднородным распределением массовой плотности из-за присутствия в нем одиночных пузырей или их пакетов.

Экспериментальное исследование

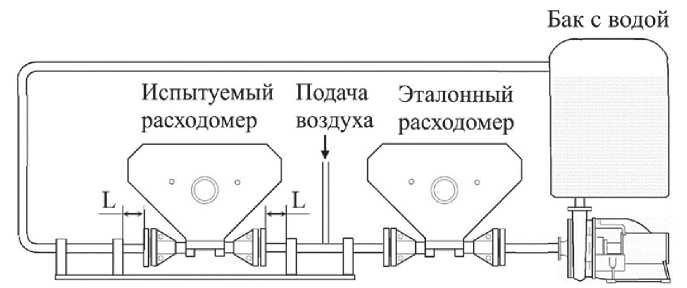
Экспериментальная установка схематически представлена на рис. 1. Она включает бак с водой, насос, эталонный и исследуемый расходомеры, систему подачи воздуха, а также комплекс аппаратуры для контроля и управления параметрами потока и автоматической записи результатов измерений. В качестве эталонного расходомера использовался коммерческий расходомер ДУ15 производства ООО «ЭлМетро Групп», а в качестве опытного – расходомер ДУ15 той же фирмы. В этих расходомерах входной поток делится пополам и попадает в две идентичные измерительные трубки, имеющие Δ-образную форму и расположенные параллельно друг другу. Поперечные вынужденные колебания трубок создаются электромеханическим приводом типа «катушка индуктивности+магнит», причем катушка закреплена в середине одной трубки, а магнит расположен напротив катушки на другой трубке, так что возбуждаемые драйвером колебания трубок происходят в противофазе. Поток флюида через колеблющуюся трубку приводит к появлению сил Кориолиса, которые возбуждают изгибные колебания каждой трубки и приводят к сдвигу фаз (или сдвигу по времени) между колебаниями их плеч. Эти сдвиги фиксируются путем сравнения показаний двух датчиков движения того же типа, что и драйвер, расположенных на трубках симметрично относительно драйвера.

Было выполнено две серии экспериментов. В первой серии изучался отклик расходомера на появление пузырьков воздуха в его измерительной трубке. Для этого системы подачи воздуха и воды настраивались так, чтобы обеспечить заданную величину объемной доли газа (gas volumefraction – GVF) в стационарном потоке флюида. После этого клапан подачи воздуха закрывали. Далее ждали, пока в трубопроводе установится стационарный однофазный поток жидкости (воды) с заданным ранее расходом. Затем кратковременно (на 0,2–0,5 с) открывали клапан подачи воздуха в промежутке между эталонным и опытным расходомерами (см. рис. 1) и записывали временные сигналы с двух измерительных катушек расходомера. Запись происходила на отрезке времени, достаточном для пробега пакета пузырьков воздуха по измерительным трубкам и возвращения системы в исходный стационарный режим. Целью второй серии экспериментов было исследование влияния газовой фазы на демпфирующие свойства колебательной системы опытного расходомера при тех же самых параметрах подачи воды и воздуха, что и в первой серии. После достижения стационарного режима выключали центральную катушку, возбуждающую колебания измерительных трубок опытного расходомера, и записывали сигналы с измерительных катушек – виброграммы затухающих колебаний.

Численные исследования

Расчетная схема модели показана на рис. 2. Здесь рассматривается геометрически простой вариант КМР с прямой измерительной трубкой кольцевого поперечного сечения. С механической точки зрения трубка описывается как защемленная по краям балка Тимошенко, совершающая вынужденные колебания под действием поперечной гармонической силы, приложенной в середине трубки (в точке C) и имеющей частоту вблизи частоты основной формы колебаний трубки с текущей средой. В присутствии среды, текущей по трубке со средней скоростью V, возникают силы инерции, приводящие к возбуждению второй (кориолисовой) формы колебаний. В резуль- тате колебания в точках A и B, симметрично расположенных относительно центра C, совершаются со сдвигом Δφ по фазе относительно друг друга. Величина Δφ непосредственно связана с массовым расходом флюида прямо пропорциональной зависимостью и поэтому является основной наблюдаемой величиной. Флюид рассматривается в простейшем приближении, когда он характеризуется всего двумя параметрами – скоростью V и плотностью ρжидк. С физической точки зрения он представляется как тонкая, но массивная нить, протягиваемая по оси трубки со скоростью V (1D-модель флюида). Подобные модели не впервые рассматриваются в литературе и достаточно хорошо изучены для случая, когда поток однофазный и стационарный, ρжидк = const, V = const [12, 13].

Насос

Рис. 1. Схема экспериментальной установки

В двухфазном потоке плотность флюида представляет собой среднее по сечению значение плотности движущихся фаз и является функцией, зависящей от выбора положения сечения (его координаты z ) и момента времени t , когда это сечение рассматривается: ρ жидк = ρ жидк ( z , t ). Существенна или нет эта зависимость, зависит от соотношения между плотностями фаз и от режима потока. Наиболее сильной она является при большой разнице в плотностях фаз и для прерывистых потоков, например, для потоков «жидкость–газ» в пробковом режиме, когда сечение трубки оказывается занятым преимущественно то одной, то другой фазой. В этом, интересующем нас, случае при не слишком больших давлениях можно считать, что плотность флюида целиком определяется плотностью жидкой фазы. Кроме того, для не слишком больших пузырей можно считать, что они движутся вдоль трубы с той же скоростью, что и жидкость [14, 15]. Последние два соображения мы положили в основу предлагаемой ниже численной модели. Фактически она является некоторым обобщением 1D модели флюида в виде массивной тонкой нити на случай, когда линейная плотность нити изменяется вдоль потока из-за присутствия легкой газовой фазы (рис. 3). Естественным способом реализовать эту модель численно является метод конечных элементов, хорошо зарекомендовавший себя при моделировании КМР в «однородном случае».

Опуская технические подробности применения FEM к интересующей нас задаче (их можно найти в работах [12, 13, 16]), отметим только, что в итоге подлежащие решению уравнения движения имеют вид:

M x + K ( V ) X + C ( V ) x = F ( t ), где M , K ( V ) и C ( V ) – глобальные матрицы масс, демпфирования и жесткости соответственно; а F ( t ) – вектор столбец внешних вынуждающих воздействий – сосредоточенных сил и моментов. Локальные матрицы, характеризующие отдельный конечный элемент, имеют размерность 4×4. Явные выражения для локальных матриц приведены в [16]. Они описывают поперечные колебания этого элемента в плоскости рисунка с учетом сил, действующих на элемент со стороны текущей среды. Степени свободы, соответствующие растяжению–сжатию, кручению и изгибу из плоскости, не учитываются.

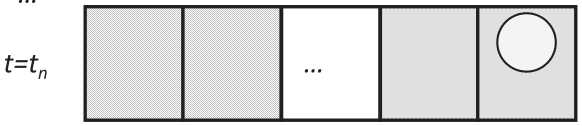
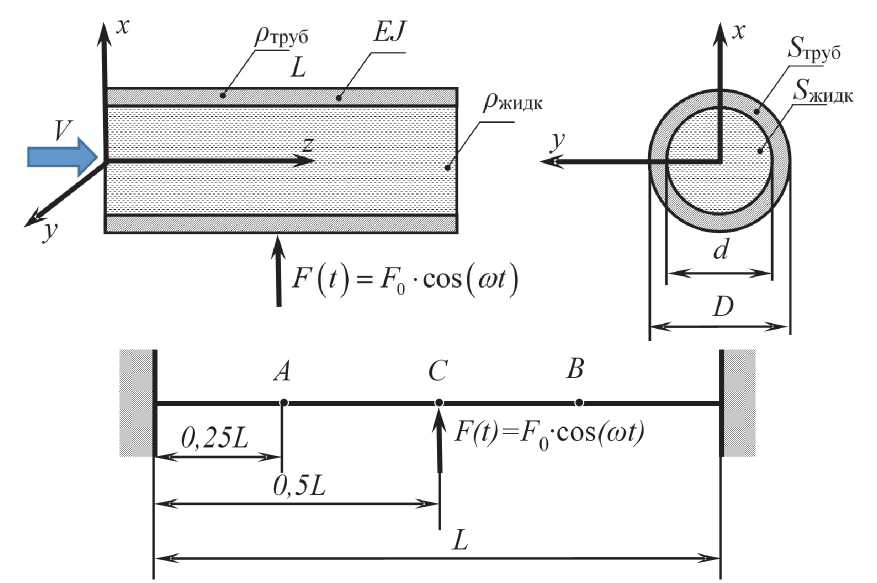
Рис. 2. Расчетная модель расходомера с прямой измерительной трубкой

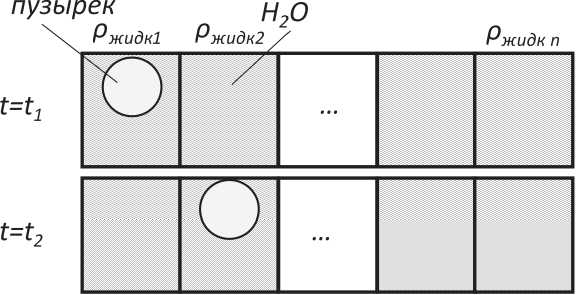
Рис. 3. Движение пузырька по трубке (расчет)

Параметры модели были подобраны так, чтобы частота основной формы колебаний трубки, заполненной неподвижной жидкостью (водой), примерно соответствовала основной частоте опытного расходомера (около 90 Гц). Для этого пришлось положить L = 800 мм, D = 11 мм, d = 9 мм, а в качестве материала трубки взять материал со свойствами ρ труб ≈ 7800 кг/м³, E ≈ 2∙10¹¹ Pa, что примерно соответствует стали. Трение в материале трубки принято прямо пропорциональным матрице жесткости. В этом случае трение является частотно зависимым, оно определялось декрементом, равным δ на собственной частоте. Трубка с такими параметрами была разбита на N = 40 элементов равной длины l = L / N . Масса флюида в каждом элементе в данный момент времени зависела от присутствия в нем пузырьков и их общего объема и считалась равномерно распределенной по длине элемента. Эта масса перемещалась вниз по потоку в соседний элемент спустя промежуток времени ∆t = l / V . При смене положения пузырька одновременно пересчитывались локальные матрицы масс, жесткости и демпфирования элементов, участвующих в обмене пузырьком, и соответственно модифицировались одноименные глобальные матрицы. В описываемых ниже численных экспериментах мы ограничились рассмотрением движения по трубке одиночного пузыря или (точнее) компактного пакета пузырьков с размерами, не выходящими за пределы одного элемента, и объемом, отвечающим заданной объемной доле газа α , в пределах этого элемента.

Вначале мы выяснили, как влияет присутствие воздушного пузыря и его положение в трубке ( z ) на частоту f 0 основной формы ее колебаний, f 0 = f 0 ( z , α ). Положив V = 0 и передвигая последовательно пузырь из одного элемента в другой, мы выполнили модальный анализ колебательной системы КРМ для каждого положения пузыря.

Если считать, что пузырь перемещается со скоростью V, тогда можно оценить, как изменяется частота f0 в зависимости от времени в процессе пробега пузыря по трубке f0 = f0( z,a = f0 (Vt,a)=f0(t,a).

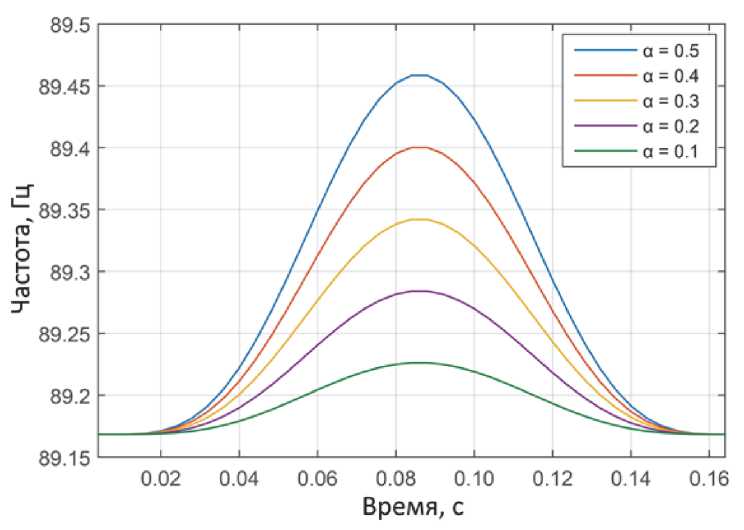
Рис. 4. Зависимость от времени собственной частоты колебаний трубки в процессе пробега по ней пузырьков разного размера (разной объемной доли газа)

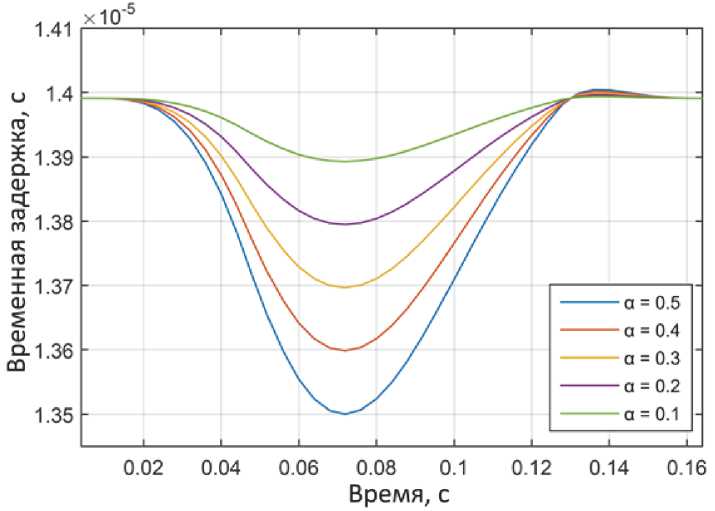
Рис. 5. Зависимость от времени временной задержки в процессе пробега по трубке пузырьков разного размера

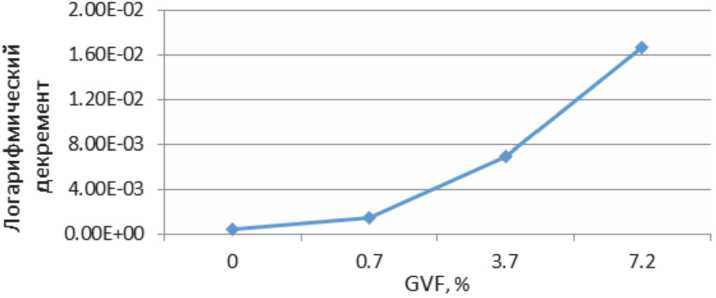
Рис. 6. Зависимость логарифмического декремента колебаний от объемной доли газа в потоке

Эта зависимость показана на рис. 4. При определении собственных частот трение в материале не учитывалось, поскольку оно мало и очень слабо влияет на собственные частоты. Из опыта также известно, что движение жидкости в трубке слабо влияет на частоту основной формы ее колебаний. Поэтому не будет большой ошибкой считать, что продемонстрированная зависимость f 0 ( z , α ) будет иметь место и в случае, когда V ≠ 0. В реальных расходомерах система управления работает таким образом, чтобы частота вынуждающей силы всегда находилась вблизи частоты основной формы колебаний трубки f 0 ( z , α ). Поэтому далее, располагая зависимостью f 0 (z,α) и уравнениями движения (1), мы выполнили гармонический анализ для каждого из N положений пузырька в рассматриваемой конечно-элементной модели. Это позволило оценить амплитуды и фазы колебаний каждого элемента в процессе пробега пузыря по трубке и, следовательно, определить измеряемую на опыте разницу фаз Δ φ в колебаниях элементов, содержащих точки A и B. (рис. 5). Как показали предварительные расчеты, декремент колебаний не влияет на Δ φ , поэтому вычисления проводились с фиксированным декрементом δ = 0,1.

Наконец, путем непосредственного численного интегрирования уравнений движения (1) был выполнен анализ переходных процессов. Рассматривалось возбуждение колебаний трубки из состояния покоя гармонической силой, приложенной в ее центре (см. рис. 1). Демпфирующие свойства трубки опытного расходомера при различной объемной доле газа в потоке были определены экспериментальным путем, как говорилось выше (см. рис. 6). Эти данные служили ориентирами в модельных расчетах. Для однофазного потока устанавливали декремент колебаний, δ = δ1 ≈ 0,0005 (см. рис. 6). Демпфирующие свойства трубок, несущих потоки «газ–жидкость», намного выше и существенно зависят от GVF. В таких случаях мы полагали в расчетах δ = δ2 ≈ 0,015 (рис. 6). В отсутствие пузырей время установления колебаний в модели с указанными выше параметрами и однофазным потоком составляло около 20 с. По его истечении декремент колебаний скачком увеличивался до δ2 и в трубке появлялся пузырь, движущийся далее так, как описано выше.

Анализ численных и экспериментальных результатов

В эксперименте расход жидкости через опытный расходомер составлял 2025 кг/ч. Поскольку расходомер содержит две трубки, а расчетная модель одну, расчеты выполнены при расходе 1012,5 кг/ч. При таком массовом расходе средняя по сечению скорость воды V в трубке составляет примерно 5 м/с. Если пузырь движется со скоростью жидкости, тогда время его пробега по трубке длиной 0,8 м будет составлять 0,16 с. На рис. 7 показаны опытные данные о движении точки на трубке, где расположен один из двух индуктивных датчиков движения, в процессе пропускания через трубку короткого пакета пузырей. На рис. 8 представлен тот же процесс пропускания пузырей, как он описывается предложенной моделью. Заметим, что наводящаяся в сенсоре ЭДС пропорциональна скорости движения трубки в месте расположения сенсора, а не ее смещению. Тем не менее графики на рисунках сравнивать можно, поскольку при колебаниях амплитуда скорости отличается от амплитуды смещения только на множитель, равный частоте колебаний. Поэтому можно заключить, что модель качественно верно передает характер отклика трубки на прохождение пузыря. Согласно рис. 7, прохождение пузыря регистрируется как узкий (шириной ≈ 0,16 с) хорошо выраженный провал на временной зависимости амплитуды ЭДС сенсора, за которым следует более длительный (≈ 3 с) период установления колебаний. Примерно столько же времени занимает процесс установления колебаний и в модели, однако предсказываемая ею глубина провала заметно меньше, чем в эксперименте, возможно, из-за малого числа конечных элементов N .

Рис. 9–12 позволяют сравнить опытные данные, полученные при пропускании через трубку пакета пузырьков, с предсказаниями модели в отношении поведения частоты колебаний на основной форме и временной задержки, обусловленной сдвигом фаз Δ φ в колебаниях сенсоров движения, располагающихся в точках A и B на рис. 2. Видно, что вновь качественное согласие имеет место, лучшее – в предсказаниях частоты и худшее – в предсказаниях временной задержки. В последнем случае, возможно, это связано с тем, что в модели подстройка частоты вынуждающей силы под частоту основной формы колебаний трубки с пузырьком не происходит, в отличие от опытного расходомера. Однако обосновать последнее утверждение можно будет после детального исследования динамических свойств системы управления этого расходомера.

Заключение

В настоящей работе в связи с исследованиями механизмов взаимодействия двухфазного потока «жидкость–газ» с измерительной трубкой кориолисова расходомера выполнены эксперименты по изучению ее реакции на появление в однородном потоке одиночных пузырей газа или их компактных пакетов. Для интерпретации полученных данных предложена простая конечноэлементная модель, в которой измерительная трубка в механическом отношении рассматривается как балка Тимошенко, а движущийся в ней двухфазный поток описывается в 1D-приближении неоднородным распределением линейной массовой плотности. Опытные данные показывают, что прохождение одиночного пузыря или пакета приводит к заметным возмущениям обеих величин, измеряемых в КРМ: частоты основной формы колебаний и сдвига фаз колебаний плеч измерительной трубки. Эти возмущения являются причиной погрешностей в определении плотности жидкой фазы и ее массового расхода. Предложенная в работе численная модель способна качественно правильно описать отклик КРМ на присутствие газовых пузырей в потоке жидкости. Совершенствование модели в количественном отношении требует более детальных исследований динамических свойств системы управления движением измерительной трубки и связи демпфирующих свойств колебательной системы с параметрами газовоздушной смеси – GVF и массовым расходом жидкости.

Испытания проведены с использованием оборудования ЦКП «Экспериментальная механика» ЮУрГУ.

Работа выполнена при финансовой поддержке Минобрнауки России  (грант

№ 9.9676.2017/8.9).

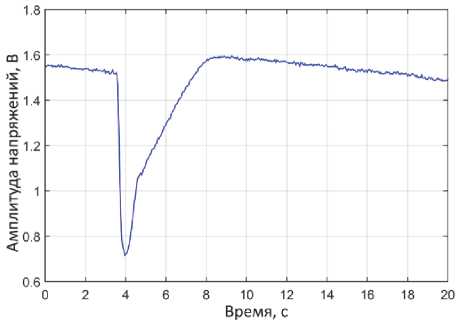
Рис. 7. Временная зависимость огибающей амплитуды ЭДС, создаваемой индуктивным датчиком движения (эксперимент)

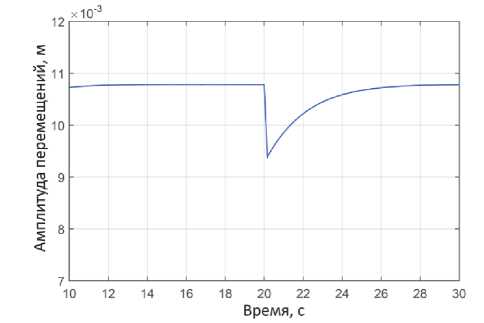
Рис. 8. Временная зависимость огибающей амплитуды смещения точки A в модели (см. рис. 2), где в реальных расходомерах расположен датчик

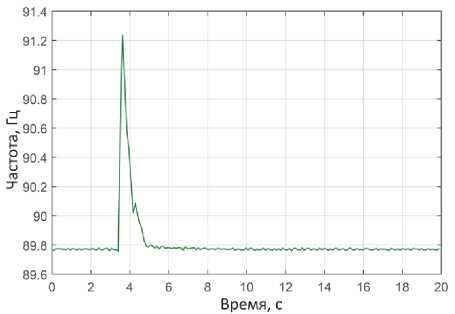
Рис. 9. Поведение основной собственной частоты колебаний трубки расходомера в процессе пробега газового пузырька в эксперименте

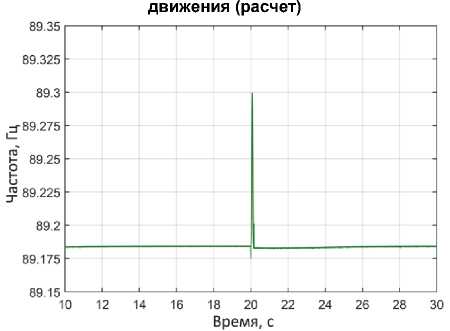
Рис. 10. Поведение основной собственной частоты колебаний трубки расходомера в процессе пробега газового пузырька в расчетной модели

Время, с

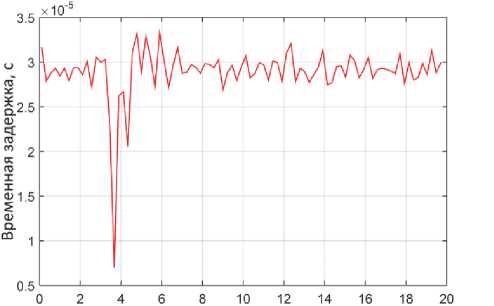
Рис. 11. Поведение временной задержки в процессе пробега газового пузырька в эксперименте

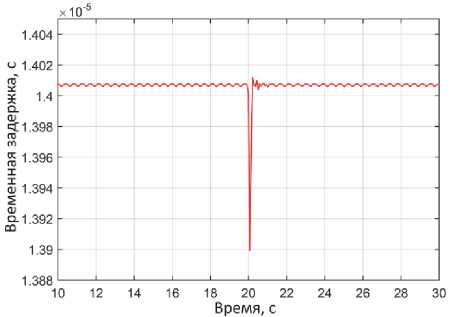
Рис. 12. Поведение временной задержки в процессе пробега газового пузырька в расчетной модели