Влияние распределения частиц по размерам на характеристики четырехволнового преобразователя излучения в прозрачной двухкомпонентной среде

Многокомпонентные среды привлекают внимание исследователей во многом благодаря высоким значениям их нелинейных показателей преломления [1–3]. При использовании четырехволновых преобразователей излучения на основе таких нелинейных сред в системах компенсации фазовых искажений необходимо установить соответствие пространственно-временных структур падающей (сигнальной) и отраженной преобразователем (объектной) волн, что позволит определить пространственные и временные масштабы неоднородностей искажающей среды, которые могут быть скомпенсированы с использованием таких преобразователей [4; 5].

В работах [6–8] проведен анализ пространственных и временных характеристик четырехволнового преобразователя излучения в прозрачной двухкомпонентной среде с учетом геометрии взаимодействия, направления распространения, расходимости волн накачки. В качестве двухкомпонентной среды рассматривалась жидкость с растворенными в ней наночастицами. Считалось, что в среде растворены частицы одного размера. Показано вырезание таким четырехволновым преобразователем излучения в спектре объектной волны полосы пространственных частот вблизи пространственной частоты второй волны накачки. Однако в нели- нейной среде всегда присутствует разброс наночастиц по размерам [9–12]. Это приводит к зависимости параметров среды (в том числе и теплофизических) от размеров частиц и может оказать существенное влияние на амплитудные и временные характеристики четырехволнового преобразователя излучения [13; 14].

Целью настоящей работы является исследование влияния распределения растворенных в прозрачной жидкости наночастиц по размерам на характеристики четырехволнового преобразователя излучения.

Рассмотрим плоский слой толщиной £ прозрачной жидкости, содержащей наночастицы. Будем считать, что в среде распространяются навстречу друг другу две плоские волны накачки с комплексными амплитудами Ai 2 (r, t ) = = A12 (z, t) exp (-iki 2 r ) и сигнальная волна с комплексной амплитудой A3. Интерференция первой волны накачки и сигнальной волны приводит к зависимости интенсивности излучения, распространяющегося в среде, от пространственных координат. Из-за явления электрострикции происходит пространственное изменение концентрации наночастиц 5C, а учет эффекта Дюфура приводит к пространственному изменению температуры среды 5T. Таким образом, в среде записывается фазовая решетка показателя пре-

качки ( A 1 2о ( t ) ) и пространственного спектра сигнальной волны ( A 4 ( к 3 , z = 0, t , a ) ) на передней

ломления.

В результате дифракции второй волны накачки на этой решетке возникает объектная волна с комплексной амплитудой A ₄ , распространяющаяся навстречу сигнальной волне и имеющая волновой фронт, комплексно-сопряженный волновому фронту сигнальной волны.

Уравнение Гельмгольца, описывающее вырожденное четырехволновое взаимодействие в прозрачной нелинейной среде, при условии,

грани нелинейного слоя, вида

A 4 ( к 4 , z = 0, t , a ) =

—

2у D 12 к dn c p v ^12 ^dT

x (k1 z - k3z )2 + (K2 - к4 )2 (k1 z — k3z )( k2z — k4z )2

^x A 20 ( t ) ^exP [ ^{— P} ( ^ t ) ] ^x

что вкладом изменения концентрации наноча-

да

I s=1

стиц в изменение комплексного показателя преломления можно пренебречь, имеет вид [6; 7]

• V ² + к ² + — — 5 T J ( a + A *1 = 0.          (1)

• (         n 0 dT Г

Здесь A = I Aj; к = tonоc 1; to — циклическая j=1

частота; n ₀ – среднее значение показателя пре-

^{1 -} ( ^{- 1} ) ^S exp [ ^{- i} ( ^k 2 z ^— k 4 z ) ^Z ]

П s        I

^{( k} 2 z ^{— k} 4 z ) ^ J

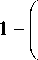
x

x

t

^D exp <-- ¹¹

c v

0 I ^p

I

I J

т j "A 10 (т') "A30 (к3

_ 0

+ ( K 2 -к 4 ) ² ( t -t ) ^x

= к 1 +к 2 - к 4 , t' ) x

ломления среды; c – скорость света в вакууме; dn

– термооптический коэффициент.

Уравнение (1) дополняется системой нестацио-

^x ( ( ^к 1 ^{- к} 3 ) ² { exp Н ( ^k 1 z - ^к 3 z ) I ] - 1 } ^{x x} Г¹ - ( ^{- 1} ) ^S ] exp Г- D 22 ( ^к 2 - ^к 4 ) ² ( ^{т - т} ‘ )

—

да

нарных материальных уравнений, описывающих изменения температуры и концентрации [6; 8]

m = 1 _

^.       ^.    2

+ (к2 — к4 )

x

авт                 9

co v---= Di iV²5 T + D V 2 5 C , p dt      ¹¹

^C = D -V 2 5 C + yV ² I , at

где C p и v — удельная теплоемкость и плотность вещества; D ₁₁ и D ₂₂ – коэффициенты теплопроводности и диффузии; D 12 и у — коэффициенты, характеризующие эффект Дюфура и явление электрострикции; I = AA * — интенсивность излучения.

2. Четырехволновое взаимодействие в прозрачной жидкости, содержащей наночастицы одного размера

В приближении заданного поля по волнам накачки (| A 1 21 >>  A 34I ), при малом коэффициенте отражения (| A 4] << I A 3I ) из уравнения Гельмгольца (1) и системы материальных уравнений (2) для нелинейной среды, содержащей наночастицы одного размера, в работе [6] полу-

чено выражение, устанавливающее связь между временной зависимостью пространственного спектра объектной волны ( A 4 ( к 4 , z = 0, t , a ) ) и временными зависимостями амплитуд волн на-

x

1 — (—1)S+m   1 — (—1)S - m s + m s — m

^{1 —} ( ^— 1 ) m exp [ ^— i ( ^k 1 z ^{— k} 3 z ) ^ ]

1 — „ ^П m . I

Ц k1 z — k3 z ) ^ J

^x exp ^ ^— D 22

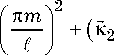
-   \2

^{— к} 4 )

x ( т — т’ ) } ) d t'

d t .

Здесь к j и k j _z — поперечная и продольная составляющие волнового вектора k_j ;

к = \^кj I, j = 1 ^ ⁴, к 4 = к + к 2 — к з ,

P ( ^z , t ) = i — dn J^{5 T} 0 ( ^z 1 , t ) ^dz 1 , n ₀ dT ₀

5 T — изменение температуры, обусловленное распространением в среде волн накачки; a – характерный размер наночастиц, определяющий значения коэффициентов диффузии, Дюфура и электрострикции нелинейной среды. Выражение (3) получено при квазиколлинеарной геоме-

трии взаимодействия (волны распространяются под малыми углами к оси Z ) при условиях неизменности температуры на гранях нелинейного

слоя и отсутствия потока частиц через эти грани.

При стационарном четырехволновом взаи-

модействии выражение для пространственного

спектра объектной волны примет вид

Av 4 ( К 4 , z = 0, a ) = - i

k y D 12 dn n 0 D 11 D 22 dT

X

* ^      ^      ^.      ^.

^X A 10 A 20 A 30 ^(к 3 = ^К 1 + ^К 2 ^{- К} 4 ) ^X

2sh (|K 2 -К 41 £ )

Л

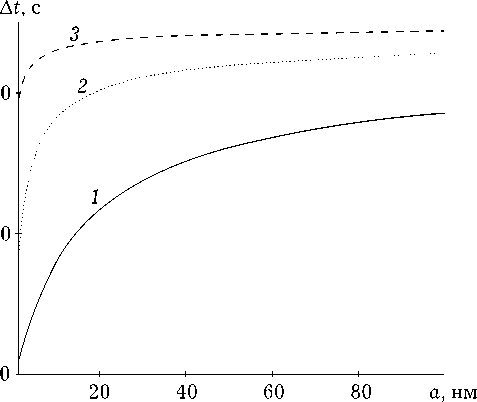
Рис. 1. Зависимость времени выхода полуширины полосы вырезанных пространственных частот от радиуса наночастиц при £ = 100 (1), 300 (2), 1000 мкм (3)

X

{ exp ^{[- i} ( ^k 1 z ^{- k} 3 z ) ^£ ] ^- exp ( ^-|^к 2 ^-К <| ^£ ) } ^X

V

exp { [|К 2 — К 41 - i ( k 2z - k 4 z ) ] £ } - 1 I ^К 2 ^{- К} 41 ^- i ^{( k} 2 z ^{- k} 4 z )

+ { exp [- i ( k i z - k 3 z ) £ ]-exp ( К 2 -К 4] £ ) } x exp Hl^K 2 ^-K4I ⁺ i ( ^k 2 z ^{- k} 4 z ) ] ^£ } ^{- 1} ' -

IК2 -К4 + i (k2z - k4z )        ^

- i exp ^(- i ^{A £} ) - 1 -.

A

Здесь A = k 1 _z + k 2 _z

-

k _{3 z}

-

k _{4 z}

–

проекция волно-

вой расстройки на ось Z .

Для сферических наночастиц в качестве характерного размера a выступает их радиус. Тогда коэффициенты диффузии, Дюфура и электрострикции определяются следующим образом [15–17]

спектр объектной волны обладает осевой симметрией АА 4 ( К 4 , z = 0, a ) = Av 4 ( -К 4 , z = 0, a ) .

В качестве нелинейной среды рассматривался слой воды ( C p = 4.2 ■ 10 3 Дж/ ( кг ■ К ) , v= 10 3 кг / м ³ , D 11 = 0.5 Вт/ ( м ■ К ) , n = 10 ^{- 3} Па ■ с, n 0 = 1.333 [15]) при температуре T = 300 К, содержащий наночастицы. Источником излучения выступала вторая гармоника Nd:YAG-лазера с длиной волны X = 532 нм.

Максимальное значение индексов суммирования при численном анализе выражения (3) опре-

k_BT ₀

D 22 =-----,

6nn a

D 12 =

3 k_BT ₀ ² S_TD ₂₂

4n C ₀ a ³

делялось из условия, что относительное отклонение амплитуды объектной волны при t ^ » на пространственной частоте К 4 = 0.1 k не превышает 0.1 %, и составляло 50.

В параксиальном приближении с ростом пространственной частоты К4 наблюдается монотон-

4лр C D 22 cn ₀ k_BT ₀ ^,

R ^S P - ⁵ 1   3

P=sZ         a ,

5 + 25; pl

ное увеличение амплитуды пространственного спектра объектной волны с последующим вы-

где P, C q — поляризуемость и концентрация наночастиц; k_B – постоянная Больцмана; T ₀ – температура среды без воздействия излучения; S t — коэффициент Соре; 5 p и 5 1 — диэлектрические проницаемости наночастиц и жидкости; П — вязкость жидкости.

В работе в качестве сигнальной волны рас-

ходом на стационарное значение. Четырехволновой преобразователь излучения «вырезает» из пространственного спектра объектной волны низкие частоты. С течением времени полуширина полосы «вырезанных» преобразователем пространственных частот ( Ак ( t , a ) ) , определяемая

сматривалась волна от непрерывного точечного

источника, расположенного на передней грани нелинейного слоя (^ А 30 ( К 3 , t ) = 1 ) . Считалось,

из решения уравнения

|AV ₄ ( к ₄ = Ак , z = 0, t , a )| =

= ^ |^ А 4 ( к ₄ = 0.1 k , z = 0, t , a )|

что волны накачки с неизменными во времени амплитудами ( JA 1 20 ( t ) = AA 1 20 ) распространяются строго вдоль оси Z ( К 1 = -К 2 = 0 ) . При такой

геометрии взаимодействия пространственный

уменьшается, выходя на установившееся значение [8].

В случае нестационарного режима четырехволнового взаимодействия с течением времени разность между полуширинами полос выреза-

емых пространственных частот, соответствующих нелинейным средам с наночастицами различных фиксированных размеров, уменьшается.

Для характеристики временной динамики пространственного спектра объектной волны введем время выхода на стационарное значение полуширины полосы «вырезанных» пространственных частот ( A t ) , определяемое из решения уравнения

Ak ( t = A t , a ) = 2 Ak ( t ^ », a ) . (7)

На рис. 1 при фиксированных толщинах среды представлены характерные зависимости времени выхода A t от радиуса наночастиц. Выход кривых на постоянное значение, связан, как следует из (3), с наличием двух механизмов (теплопроводность и диффузия), влияющих на временную динамику пространственного спектра объектной волны. При малых размерах наночастиц временная динамика связана в основном с диффузией частиц, что приводит с ростом их радиуса к уменьшению согласно выражениям (5) коэффициента диффузии и увеличению времени выхода полуширины полосы вырезанных пространственных частот на стационарное значение. При больших размерах наночастиц основное влияние на временную динамику пространственного спектра объектной волны оказывает теплопроводность, время выхода A t перестает зависеть от размера a .

Представленные на рис. 1 зависимости времени выхода A t от радиуса наночастиц хорошо аппроксимируются выражением

A t ( a ) = P i arctg [р₂ ( a + P 3 ) ]. (8)

Численный анализ временной динамики пространственного спектра объектной волны показывает, что при фиксированном размере наночастиц зависимость времени выхода A t от толщины нелинейного слоя можно аппроксимировать выражением

A t ( £ ) = a 1 { 1 - exp [-a₂ ( £ + а з ) ] } . (9)

Уменьшение полуширины полосы вырезаемых пространственных частот с ростом толщины нелинейной среды объясняет увеличение с ростом £ времени A t .

Выражения (8) и (9) справедливы для диапазонов толщин среды £ от 300 мкм до 1 мм и радиуса наночастиц a от 1 до 100 нм соответственно. Коэффициенты, входящие в выражение (9), для радиусов частиц a = 1, 10, 50 нм принимают значения соответственно a i = 20.4, 23, 24.15 с; а₂ = 2.7 ■ 10 3 , 4.9 ■ 10 3 , 5.1 ■ 10 3 м, а₃ =-1.4 ■ 10 ^{- 4} ,

-10 ⁵ , 1.1 ■ 10 ⁴ м. Коэффициенты в (8) для толщин среды £ = 100, 300, 1000 мкм принимают значения P i = 12.8, 14.9, 16.8 с; Р 2 = 6.7 ■ 10 ⁷ , 1.9 ■ 10 8 , 3.8 ■ 10 8 м ^{- 1} ; Р₃ = 10 ^{- 9} , 6 ■ 10 ^{- 9} , 9 ■ 10 ^{- 9} м.

Рассмотрим четырехволновое взаимодействие в жидкости, в которой доля наночастиц, имеющих радиус a , меняется в соответствии с функцией распределения f ( a ) . Тогда пространственный спектр объектной волны на передней грани нелинейного слоя можно представить в виде когерентной «суммы» пространственных спектров

A4 (К4, z = 0, t) = a2

= J A 4 ( К 4 , z = 0, t , a ) f ( a ) da .

a ₁

Здесь a ₁ и a ₂ – наименьший и наибольший радиус наночастиц, присутствующих в среде.

Из выражения (10) с учетом (4) и (5) следует, что при стационарном четырехволновом взаимодействии учет распределения частиц по размерам не влияет на пространственную селективность четырехволнового преобразователя излучения, меняется лишь амплитуда объектной волны и, следовательно, амплитудный коэффициент отражения

R =

A 4 ( К 4 = 0.1 k , z = 0) _

^A 30 ^(k 3 )

a 2 1

= G £     f ( a ) da .

a a1

Здесь

G =

^kkB^T0 S T ^s 1 ( e p ^- s 1 ) d_n

2ПП cnD 11 ( e p + 2S 1 ) ^dT

/-V         /-V

A 10 A 20 .

Предположим, что распределение наночастиц

по размерам описывается нормальным распределением [14]

f ( a ) =

f 0

V2na

exp

(a - a0 )2 2g2

где a 0 — средний радиус наночастиц; g — дисперсия; f ₀ – коэффициент, определяемый объемом частиц в жидкости.

Анализ выражения (10) с учетом (3) и (12) показывает, что характер временной зависимости

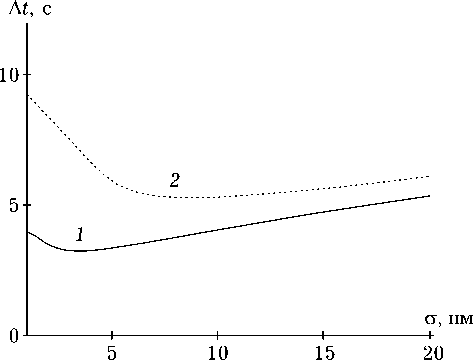
Рис. 2. Зависимость времени выхода полуширины полосы вырезанных пространственных частот от дисперсии в нормальном распределении наночастиц по размерам при толщине среды 100 мкм и среднем радиусе частиц 5 (1), 10 нм (2) пространственного спектра объектной волны как при наличии в нелинейной среде наночастиц одного размера, так и в случае распределения частиц по размерам качественно совпадает.

На рис. 2 приведены характерные зависимости времени выхода A t от дисперсии в нормальном распределении наночастиц по размерам.

При фиксированном среднем радиусе наночастиц и толщине среды с ростом дисперсии время выхода полуширины полосы вырезанных четырехволновым преобразователем излучения пространственных частот вначале убывает, достигает минимального значения, затем возрастает с последующим выходом на зависимость, близкую к линейной. Коэффициент пропорциональности в такой зависимости определятся в основном толщиной среды и слабо зависит от среднего размера наночастиц.

При увеличении среднего размера наночастиц от 5 до 10 нм положение минимума a min в зависимости A t от дисперсии в нормальном распределении смещается в область больших значений, не превышая при этом среднего размера частиц (C min <  a ₀).

На рис. 3 представлены зависимости коэффициента отражения от дисперсии при различных средних размерах наночастиц. Положение и величина максимума коэффициента отражения существенным образом зависит от минимального размера частиц a ₁ , учитываемого при интегрировании выражения (10), среднего размера a ₀ и слабо зависит от максимального размера частиц a ₂. При расчете кривых считалось, что размер наночастиц меняется от a i = 1 нм до a 2 = 100 нм. Для кривых 1, 2 и 3, приведенных

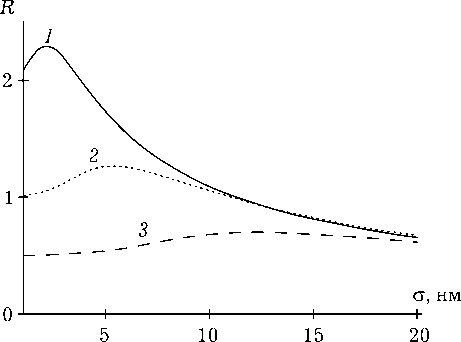
Рис. 3. Зависимость коэффициента отражения от дисперсии при Gf = 10 ^{- 6} , £ = 1000 мкм, a 0 = 5 (1), 10 (2) и 20 нм (3)

на рис. 3, максимальное значение амплитудного коэффициента отражения больше значения коэффициента отражения при условии, что в нелинейной среде находятся частицы одного размера ( а ^ 0 ) , на 14.5 %, 26 % и 40 % соответственно.

Наличие экстремальных точек в зависимостях коэффициента отражения, времени выхода A t от дисперсии в распределении частиц имеет следующее физическое объяснение.

При а <  a 0 с увеличением дисперсии в распределении наночастиц по размерам возрастает вклад в пространственный спектр объектной волны пространственных спектров волн, наличие которых связано с частицами «малых» размеров ( a <  a 0 ). Обратно пропорциональная зависимость амплитуды пространственного спектра от размера наночастицы, увеличение с уменьшением размера частицы скорости записи динамических решеток приводит к увеличению коэффициента отражения, уменьшению времени выхода полуширины полосы вырезанных пространственных частот на стационарное значение. При дальнейшем увеличении дисперсии в распределении наночастиц по размерам (а >  a 0 ) доля частиц с размерами от a ₁ до a ₀ уменьшается, возрастает вклад в пространственный спектр объектной волны пространственных спектров волн, связанных с частицами «больших» размеров ( a >  a 0 ). В результате этого время выхода полуширины вырезанных пространственных частот на стационарное значение начинает плавно увеличиваться, а амплитудный коэффициент отражения уменьшаться.

Показано, что для четырехволнового преобразователя излучения в прозрачной двух- компонентной среде, состоящей из жидкости и наночастиц, учет распределения частиц по размерам, не меняя характера динамики пространственного спектра объектной волны, оказывает существенное влияние на величину амплитудного коэффициента отражения, время выхода полуширины полосы вырезанных пространственных частот на стационарное значение. Увеличение дисперсии в распределении наночастиц по размерам приводит вначале к росту, а затем к уменьшению амплитудного коэффициента отражения. При этом время выхода полуширины полосы вырезаемых пространственных частот вначале уменьшается, а затем плавно увеличивается. Увеличение среднего радиуса наночастиц приводит к смещению экстремумов в зависимостях At (ст) и R (ст) в область больших дисперсий.

• 1.    Smith P.W., Ashkin A., Tomlinson W.J. Four-wave mixing in an artificial Kerr medium // Optics Letters. 1981. Vol. 6. № 6. P. 284-286.

• 2.    Freysz E., Laffon E., Ducasse A. Pase conjugation used as a test of the local andnonlocal characteristics of optical nonlinearities of microemulsions // Optics Letters. 1991. Vol. 16. № 21. P. 1644—1646.

• 3.    Концентрационная нелинейность суспензии прозрачных микросфер под действием градиентной силы в поле периодически модулированного лазерного излучения / А.А. Афанасьев [и др.] // Квантовая электроника. 2016. Т. 46. № 10. С. 891—894.

• 4.    Компенсация фазовых искажений при вырожденном четырехчастотном взаимодействии / Э.С. Воронин [и др.] // Квантовая электроника. 1979. Т. 6. № 9. С. 2009—2015.

• 5.    Дмитриев В.Г. Нелинейная оптика и обращение волнового фронта. М.: Физматлит, 2003. 256 с.

• 6.    Ивахник В.В, Савельев М.В. Пространственная селективность четырехволнового преобразователя излучения в прозрачной двухкомпонентной среде в схеме с попутны-

  ми волнами накачки // Компьютерная оптика. 2016. Т. 40. № 3. С. 322—330.

• 7.    Ivakhnik V.V., Savel’ev M.V. Degenerate four-wave mixing in transparent two-component medium considering spatial structure of the pump waves // Journal of Physics: Conference Series. 2016. Vol. 737. P. 012007.

• 8.    Ивахник В.В, Савельев М.В. Нестационарное четырехволновое взаимодействие в прозрачной двухкомпонентной среде // Компьютерная оптика. 2018. Т. 42. № 2. С. 227–235.

• 9.    Smith P.W., Maloney P.J., Ashkin A. Use of a liquid suspension of dielectric spheres as an artificial Kerr medium // Optics Letters. 19 8 2. Vol. 7. № 8. P. 34 7—349.

• 10.    Bloemer M.J., Haus J.W., Ashley P.R. Degenerate four-wave mixing in colloidal gold as a function of particle size // Journal of the Optical Society of America B. 1990. Vol. 7. № 5. P.790 —795.

• 11.    Wu J., Xiang D., Gordon R. Characterizing gold nanorods in aqueous solution by acoustic vibrations probed with four-wave mixing // Optics Express. 2016. Vol. 24. № 12. P. 12458–12465.

• 12.    Four-wave-mixing approach to in situ detection of n anoparticles / A. Gerakis [et al.] // Physical Review Applied. 2018. Vol. 9. P. 014031.

• 13.    Optical nonlinearities of a high concentration of small metal particles dispersed in glass: copper and silver particles / K. Uchida [et al.] // Journal of the Optical Society of America B. 1994. Vol. 11. № 7. P. 1236—1243.

• 14.    Жукова В.А., Ивахник В.В., Никонов В.И. Запись динамической голограммы в обратимой ФХС с учетом распределения фотохромных частиц по нормальному закону // Вестник СамГУ. 1998. № 4(10). С. 160—165.

• 15.    Ливашвили А.И., Костина Г.В., Якунина М.И. Динамика температуры прозрачной наножидкости, находящейся под воздействием периодического светового поля // Оптический журнал. 2013. Т. 80. № 2. С. 71—74.

• 16.    Де Гроот С., Мазур. П. Неравновесная термодинамика. М.: Мир, 1964. 456 с.

• 17.    Tabiryan N.V., Luo W. Soret feedback in thermal diffusion of suspension // Physical Review E. 1998. Vol. 57. № 4. P. 4431–4440.

Influence of the particle size distribution on the characteristics of a four-wave radiation converter in a transparent two-component medium

K.N. Aldebeneva, V.V. Ivakhnik, M.V. Savelyev