Влияние расстройки и керровской нелинейности на атом-атомное перепутывание в двойной двухфотонной модели Джейнса - Каммингса

Перепутывание является фундаментальным понятием квантовой физики, играющим ключевую роль как для понимания роли нелокальных корреляций в квантовой механике, так и для практических приложений в физике квантовых вычислений и квантовых коммуникаций [1]. Потому в последние годы было потрачено много усилий для изучения как свойств и количественных мер перепутывания квантовых объектов различной физической природы, так и механизмов контроля и управления перепутанными состояниями. Квантовая электродинамика резонатора (РКЭД) является приоритетным инструментом для исследований перепутанных состояний кубитов, взаимодействующих с квантовыми полями резонаторов. В последние годы удалось экспериментально наблюдать перепутанные состояния кубитов на нейтральных атомах, ионах в магнитных ловушках, сверхпроводящих кольцах, квантовых точках и примесных спинах [2]. Теоретические исследования систем кубитов, взаимодействующих с выделенными модами резонаторов, основаны на модели Джейнса – Каммингса (МДК) и ее обобщениях [3]. Хорошо известно, что модель Джейнса – Каммингса (МДК) является простейшей из возможных физических моделей, которая описывает взаимодействие естественного или искусственного двухуровневого атома (кубита)

с одномодовым полем резонатора и может быть использована для описания широкого круга явлений в квантовой оптике и конденсированных средах. Для того чтобы исследовать более широкий спектр явлений, обусловленных взаимодействием кубитов с квантовыми полями резонаторов, в последние годы были рассмотрены многочисленные обобщения МДК (см. ссылки в [4]). Йонак и соавторы [4; 5] предложили так называемую двойную модель Джейнса – Каммингса (ДМДК), которая состоит из двух двухуровневых атомов (кубитов) и двух резонаторных мод при условии, что каждый атом взаимодействует только с одним полем. Они обнаружили, что для слабых малофотонных полей резонаторов перепутывание кубитов не является стабильным, парметр перепутывания кубитов испытывает периодические осцилляции Раби, при этом наблюдается эффект мгновенной смерти перепутывания. В последнее время ДМДК была тщательно исследована (см. ссылки [6; 7]). При этом было показано, что керровскпя нелинейность среды резонатора может использоваться для усиления максимальной степени перепутывания кубитов и для подавления эффекта мгновенной смерти перепутывания. Однофотонная двойная модель Джейнса – Каммингса может быть расширена до нелинейной версии, известной как двухфотонная ДМДК [9]. В последнее время в ряде работ было показано, что расстройка может также быть использована для стабилизации атом-атом-

ЕЁ^М © Захаров Р.К., Башкиров Е.К., 2021

ного перепутывания [22–24]. В данной работе мы провели исследование влияния расстройки между атомами и двойной частотой мод полей и керровской нелинейности в обоих модах резонаторов на атом-атомное перепутывание для различных перепутанных начальных атомных состояний в рамках двухфотонной ДМДК.

1.    Модель и ее точное решение

Рассмотрим два идентичных двухуровневых атома (кубита), которые будем обозначать как A и B с энергетической щелью btog, и две одинаковые независимые резонаторые моды двух копла-нарных микроволновых резонаторов, которые будем обозначать как а и b, с частотами to a = tob = to. Пусть кубит A нерезонансно взаимодействует с полем одномодового резонатора а, а кубит B нерезонансно взаимодействует с полем одномодового резонатора b. Положим, что оба взаимодействия носят двухфотонный характер. Выберем для рассмотрения случай, когда константы связи между кубитами и полями равны. Пусть в обоих резонаторах также имеется дополнительная среда Керра. В системе отсчета, вращающейся с удвоенной частотой мод полей, гамильтониан данной системы в приближении вращающейся волны может быть представлен в виде

H = (1/2) й Л ( о A + g B ) + й у a ( ^ A a ² + a ^{+ 2} g _a ) + + й у b G b ² + b ⁺² G _B ) + х a a ^{+ 2} a ² + х b b ^{+ 2} b ²,

где (1/ 2)g Z - оператор инверсии в i -м кубите ( i = A , B ); a + = | +) ii (- | и g - = | -) ii (+ | - операторы перехода между возбужденным | +) i и основным | -) i состояниями в i -м кубите; a ⁺ и a - операторы рождения и уничтожения фотонов моды резонатора а ; b ⁺ и b - операторы рождения и уничтожения фотонов моды резонатора b ; у _a -постоянная связи между кубитом A и модой резонатора а ; у b - постояная связи между кубитом B и модой резонатора b ; х _a - параметр керровской нелинейности для резонатора а ; х b - параметр керровской нелинейности для резонатора b , и 5 = to o - 2 to - расстройка. Положим для простоты

Y a = Y b = Y , х a = х b = х .

Выберем в качестве начального состояния двух кубитов перепутанное состояние белловского типа

| ^ (0) ) a = cos 9 I + , -) + sin 9 I - , +)                        (2)

или

| ^ ^{(0) )} a = ^{cos 9} | ⁺ , ^{+) + sin 9} | ^- , ^-) ,                       ⁽³⁾

где 9 - параметр, определяющий степень начального перепутывания кубитов. Для перепутанных состояний 0 < 9 < п . В случае 9 = 0 или 9 = п кубиты находятся в одном из сепарабельных состояний.

В качестве начального состояния полей резонаторов выберем вакуумное состояние 10,0 ) . Тогда полное начальное состояние для рассматриваемой модели имеет вид

| W) ) =| ^ (0) ) A ® |0,0 ) ,                                (4)

или

| W) ) =| ^ (0) ) а ® |0,0 ) .                                (5)

Решая квантовое уравнение Лиувилля, мы можем найти временную волновую функцию системы. Для начального состояния (4) временная волновая функция может быть представлена в следующей форме:

| У ( t ) ) = X^ ( t )| + , - ;0,0 ) + X ₂ ( t )| - , + ;0,0 ) + ¹²      (6)

⁺ X 3⁽ t ) | ^- , ^{- ;2,0 ) +} X 4⁽ t ) | ^- , ^{- ;0,2 )} .

Здесь

X 1(t) = cos9e-i(2х-5)t/2 X х [Q3 cos(Q3t /2) + i(2х -5)sin(Q3t /2)] / Q3,

X2 (t) = sin 9e-i(2х-5)t/2 x x [Q3 cos(Q3t /2) + i(2х -5)sin(Q3t /2)] / Q3,

X ₃( t ) = i cos 9 2V2 Y e " i ^{(2 х-5 )} t ^/2 sin( Q ₃ t /2)/ Q 3 ,

X4(t) = -isin92^ye~i(2х-5)t/2 sin(^31 / 2)/ Q3, где Q3 = V(5- 2х)2 + 8y2 и 5 = Л / у, j< = х / Yb.

Для начального состояния (5) временная волновая функция имеет вид

| ^ ( t ) ) = X 1 ( t )| + , + ;0,0 ) +

⁺ X 2⁽ t ) | ^- , ^{- ;0,0 ) +} X 3⁽ t ) | ⁺ , ^{- ;0,2 ) +                    (7)}

⁺ X 4⁽ t ) | ^- , ^{+ ;2,0 ) +} X 5⁽ t ) | ^- , ^{- ;2,2 )} .

Здесь

X 1 ( t ) = cos 9 e ^{- 2}i ^х t [4 Y ² +q 5 cos( Q 4 1 ) +

+ (2 х -5 ) Q 4 sin( Q 4 Y t )]/ Q 4 ,

X 2 ( t ) = sin 9 e i ⁵ t ,

X3(t) = X4(t) = 2 cos 9ye-2iхt х x [2(2х - 5)sin2(Q41 / 2) - iQ4 sin(Q41)] / q4 , X 5( t) = cos 9y2 e -2 iх t [1 - cos(Q41)] / q4 , где Q4 =(1/2)Q3.

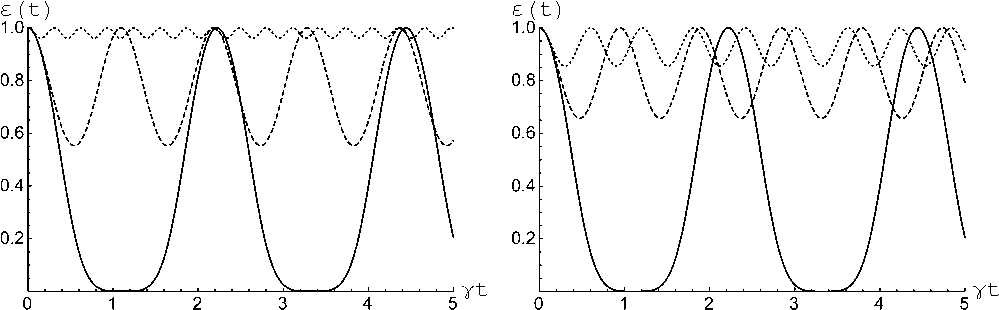
Рис. 1. Отрицательность как функция безразмерного времени у t для начального перепутанного атомного состояния (2). Параметр x = 0, расстройка 6 = 0 (сплошная), 6 = 5 (пунктирная), 6 = 20 (точечная) ( а ); расстройка 5 = 0, x = 0 (сплошная), x = 3 (пунктирная), x = 5 (точечная) ( б) . Параметр 6 = п /4

Fig. 1. Negativity as a function of dimensionless time у t for the initial entangled atomic state (2). Parameter, x = 0, detuning, 6 = 0 (solid), 6 = 5 (dashed), 6 = 20 (dotted) ( a ); detuning, 6 = 0, x = 0 (solid), x = 3 (dashed), x = 5 (dotted) ( b ).

Parameter 6 = п /4

2.    Перепутывание кубитов

Для двухкубитной системы, описываемой матрицей атомной плотности р a ( t ), мера перепутывания или отрицательности может быть определена в терминах отрицательных собственных значений ц ^- частично транспонированной реду-

T цированной атомной матрицы плотности ( р A ) [25; 26]

8 = - 2 ^ ц - .                                      (8)

В случае, когда 8 = 0, два кубита являются сепарабельными (т. е. они неперепутаны), а условие 8 > 0 означает наличие атом-атомного перепутывания. Случай 8 = 1 указывает на максимальную запутанность.

Используя временную волновую функцию, можно получить полную матрицу плотности для всей системы в виде р ( t )=| ^ ( t ))W t )|.

Взяв след по полевым переменным от полной матрицы плотности, можно получить редуцированную атомную матрицу плотности. Для начального состояния (4) она имеет вид

	Г 0     0       0            0        ^
	0 | X 1 |2   X 1 X 2           0
рЛ( t ) = A		.            (9)
	0 X 2 X* 1 | X 212         0
	0     0        0     | X, |2 + 1 X4 |2 у                          3        4 у

Частично транспонированая по переменным одного кубита редуцированная атомная матрица плотности для (9) имеет вид

	0	0	0	X 2 X *
T , X	0	| X 1 |2	0	0
р A ( t ) =		1	.          .9		. (10)
	0	0	| X 2 |2	0
	[ X i X 2	0	0	| X 3 |2 + | X 4 |2 У

Матрица (10) имеет только одно собственное значение, которое может быть отрицательным. В результате в рассматриваемом случае отрицательность можно записать в виде

8 ( t ) = V(I X з |² + I X 4 | 2 )² + 4| X 1 X 2 |² -- | X з |² - | X 4 |² •

Для начального состояния (5) редуцированная матрица плотности имеет вид

	Г | X 1 |2     0       0          X 1 X 2
	0     | Xo |2     0             0
р A ( t ) =	3 ।           .9	. (12)
	0        0     | X 4 |2          0
	ч X * X 2      0       0     | X 2 |2 + | X 5 |2?

Частично транспонированная по переменным одного кубита редуцированная атомная матрица плотности для (12) принимает вид

	| X 1 |2     0        0             0
т	0    | X o |2   XX *         0
р А '( t ) =	3    12	. (13)
	0     X 1 X 2   | X 4 |2         0
	Ч 0        0         0      | X 2 12 + 1 X 5|2 у

Матрица (13) также имеет только одно собственное значение, которое может быть отрицательным. В результате в рассматриваемом случае отрицательность можно записать как

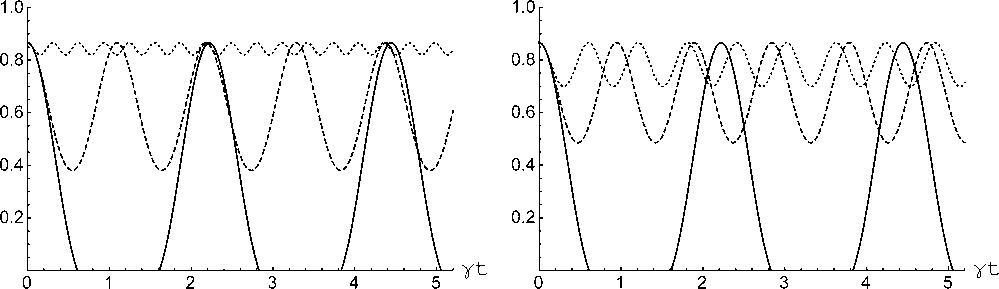
а                                                   б

Рис. 2. Отрицательность как функция безразмерного времени γ t для для начального перепутанного атомного состояния (3). Параметр x = 0, расстройка 5 = 0 (сплошная), 5 = 5 (пунктирная), 5 = 20 (точечная) ( а ); расстройка 5 = 0, x = 0 (сплошная), x = 3 (пунктирная), x = 5 (точечная) ( б) . Параметр 6 = п /6

Fig. 2. Negativity as a function of dimensionless time у t for the initial entangled atomic state (3). Parameter, x = 0, detuning, 5 = 0 (solid), 5 = 5 (dashed), 5 = 20 (dotted) ( a ); detuning, 5 = 0, x = 0 (solid), x = 3 (dashed), x = 5 (dotted) ( b ).

Parameter θ = π /6

_£ ( t ) = V (\ X 2 \² + | X 5\² )² + 4| X 1 X 2 \² -- | X 2 \² - | X 5 \² .

Результаты численного моделирования параметров перепутывания кубитов (11) и (14) представлены на рис. 1 и 2.

3.    Результаты и обсуждение

Отрицательность для запутанного начального атомного состояния (2) изображена на рис. 1, a как функция безразмерного времени уt для резонаторов, в которых отсутствует керровская среда, т. е. % = 0, и различными значениями параметра расстройки. Представлены графики для значений параметра расстройки δ =0 (сплошная линия), δ/γ=5 (пунктирная линия) и δ/ γ= 20 (точечная линия). На рис. 1, б показана временная завис-мость отрицательности для начального состояния (2) резонансного взаимодействия кубитов с полями, т. е. для модели для случая 5 = 0, и различные значения коэффициента керровской нелинейности x = 0 (сплошная линия), x / У = 3 (пунктирная линия) x / У = 20 (точечная линия) Для всех кривых, представленных на рис. 1, параметр θ= π/4. Из рис. 1 хорошо видно, что для рассматриваемого начального состояния отсутствует эффект мгновенной смерти перепутывания для любых значений парметров модели (указанная особенность имеет место и для любых других значений парамера 0 < 6 < п). Из рис. 1 также видно, что с увеличением расстройки или коэффициента керровской нелинейности флуктуация отрицательности уменьшается. Следовательно, расстройка и керровская нелинейность могут стабилизировать наведенное перепутывание между двумя кубитами, что может быть полезным в осуществлении контроля за степенью атом-атомного перепутывания. Поведение параметра отрицательности для начального перепутанного атомного состояния (3) и 6 = п /4 аналогично для начального состояния (2). На рис. 2 показана отрицательность как функция безразмерного времени уt для начального атомного состояния (3) и 6 = п /6. На рис. 2, а рассмотрена модель без керровской среды, т. е. x = 0, а параметр расстройки выбран равным: δ =0 (сплошная линия), δ/γ=5 (пунктирная линия), 5 / у = 20 (точечная линия). Соответственно, на рис. 2, б 5 = 0, а коэффициенты керровской нелинейности равны: x = 0 (сплошная линия), Х / у = 3 (пунктирная линия) и x / У = 20 (точечная линия). Из рис. 2 видно. что в рассматриваемом случае возникает эффект мгновенной смерти перепутывания. Мгновенная смерть перепутывания – это исчезновение перепутывания состояний атомов на временах, меньших времени декоге-ренции изучаемой системы. При увеличении расстройки или коэффициента керровской нелинейности эффект мгновенной смерти перепутывания исчезает. Это означает, что как расстройка, так и керровская среда могут эффективно подавлять этот эффект.

Заключение

В этой статье мы исследовали перепутывание между двумя идентичными кубитами, которые взаимодействуют с двумя независимыми модами копланарных идеальных резонаторов посредством двухфотонных переходов. Мы учли расстройку и керровскую нелинейность в обеих модах. Мы рассмотрели два начальных перепутанных атомных состояния белловского типа и вычислили временное поведение отрицательности для различных значений параметров модели. Результаты показывают, что оба эти параметра оказывают большое влияние на поведение параметра перепутывания кубитов. Наличие расстройки и керровской нелинейности приводит к стабилизации перепутывания для всех начальных атомных состояний белловского типа. Для начального перепутанного состояния кубитов вида (3) расстройка и наличие керровской среды в резонаторах могут предотвратить нежелательный эффект мгновенной смерти перепутывания состояний кубитов.