Влияние разгрузочных щелей на напряженное состояние и ползучесть породного массива в окрестности выработки

Горные выработки нарушают целостность породного массива, влекут за собой перераспределение напряжений в нем, обусловливают концентрацию напряжений, которая становится причиной ползучести стенок выработки. Практикуется целый ряд способов изменения нежелательного поля напряжений в породном массиве или принимаются меры для повышения его предельных характеристик вблизи стенок выработки [1–3]. Одним из способов влияния на напряженное состояние породного массива является создание разгрузочных щелей, выбираемых в направлении нормали к стенкам выработки [4–8]. Экспериментальные исследования [4, 5] подтверждают эффективность применения такого приема. Результаты численных экспериментов по исследованию влияния разгрузочных щелей на поведение угольного пласта и соляных пород приводятся в работах [6–8].

В данной работе на примере горизонтальной выработки кругового сечения изучается влияние одиночной разгрузочной щели и нескольких взаимодействующих разгрузочных щелей на напряженное состояние и ползучесть примыкающего к стенкам выработки породного массива. Исследование проводится численно в пространственной

постановке. Пространственная постановка обусловлена тем, что в физически нелинейных задачах, когда материальные свойства среды зависят от инвариантов тензора возникающих в ней напряжений, использование допущения о возможности описания поведения массива в двумерной постановке приводит к ошибочному результату из-за значительного влияния нормальных напряжений в направлении оси выработки на величину интенсивности напряжений [9].

Принимается, что породный массив ведет себя как физически нелинейная наследственная среда, которой отвечают физические уравнения, построенные в работе [9]:

1 ^t

^ij (t) = "^sij (t)-HC (t,°*,°*)sj + jKC (t-T,°(T),°i (T))sij (T)dT,

2G

1 ^t

^(t) = —°(t)-Hv (t,°*,°*)°* + jKv (t-T,°(t),°i (t))°(t)dt.(2)

B ₀

Здесь t — момент времени, с которого учитывается наличие выработки; ^ ij и с — компоненты девиатора деформаций и объемная деформация, отвечающие перемещениям, отсчитываемым от состояния среды в нетронутом массиве; G и B –– мгновенные модули сдвига и объемной упругости; s ij и ° — компоненты девиатора напряжений и нормальное напряжение на октаэдрической площадке; ° i — интенсивность напряжений; символ « * » обозначает параметры нетронутого массива; K_C и K_V — ядра сдвиговой и объемной ползучести; H_C и H_V — функции , описывающие влияние напряжений в нетронутом массиве на его напряженно-деформированное состояние в момент времени t :

1 ^t

H c ( t , ° , ° J=47 ⁺ j K c ( t ^-T , ° , ° i ) ^{d T} ,                                            (3)

2 G ₀

1 ^t

H v ( t , ° * , ° * ) = — + j K v ( t -t , ° * , ° * ) d t .                                                (4)

B ₀

Далее в настоящей работе используются материальные параметры и функции сдвиговой ползучести сильвинита пласта Кр. II Второго Соликамского рудника, полученные авторами работы [10]. Объемная деформация массива принимается линейно упругой с модулем К = 1,33 - 10 3 МПа . Мгновенный модуль Юнга породы составляет Е = 1,6 - 10 3 МПа. Рассматриваемая среда является физически линейной, если интенсивность напряжений удовлетворяет неравенству ° i <  0,4 ° _сж ( ° _сж = 24,75 МПа — предел прочности при сжатии), в этом случае среда проявляет ограниченную ползучесть. Если же ° i >  0,4 ° _сж, то физические свойства среды нелинейны, а ползучесть при таком уровне напряжений оказывается неограниченной. Исходя из приведенных в работе [11] опытных данных, свидетельствующих, что напряженное состояние целостного соляного массива практически гидростатическое, в данной работе считается, что в точках нетронутого породного массива формируются напряжения всестороннего сжатия величиной γ h ( γ –– удельный вес породы, h –– глубина ее залегания).

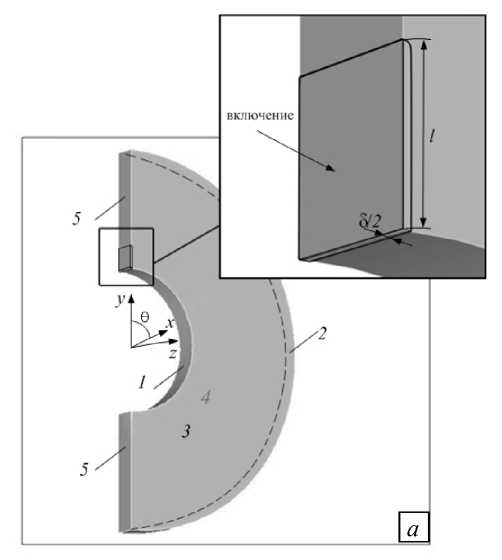
Пусть в соляном массиве, находящемся в начальном напряженном состоянии, проходится горизонтальная выработка кругового сечения (радиус r = 1,5 м). Через Н –– расстояние от земной поверхности до оси выработки, обозначается глубина залегания выработки. В окрестности верхней точки выработки в направлении нормали к ее поверхности часть массива (глубиной l и шириной 5 ) извлекается и заполняется другой средой (или оставляется незаполненной). В результате образуется разгрузочная щель. В рамках данной работы рассматриваются заполненные щели; заполняющий материал (включение) считается упругим, его модуль упругости E' полагается на два порядка меньшим мгновенного модуля массива. Задача состоит в анализе влияния разгрузочной щели на напряженное состояние и ползучесть массива вблизи контура выработки.

а

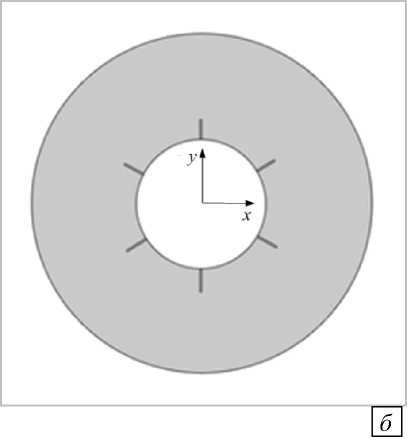
Рис. 1. Расчетная область соляного массива в окрестности цилиндрической выработки с одной разгрузочной щелью (включением) ( а ) и шестью щелями ( б)

Решение находится в пространственной области, вырезанной из массива двумя соосными цилиндрическими поверхностями 1 и 2 , двумя плоскостями 3 и 4 , ортогональными оси выработки, и вертикальной плоскостью 5 , проходящей через ее ось (Рис. 1). Начало декартовой ортонормированной системы координат xyz находится в центре области решения, ось z направлена по оси выработки, ось у — вертикально вверх. Вводится также цилиндрическая система координат r 0 z , ось z которой совпадает с одноименной осью декартовой системы, а угол 0 отсчитывается против часовой стрелки от оси x в плоскости xy .

Граничные условия формулируются следующим образом:

• -    условия симметрии на поверхностях 3 ,    4 ,    5 :    u_zz = 0, о _zr = 0, ст _{z 0} = 0 ;

u zz = ⁰ , ^о zr = ⁰ , ° z 0 = ⁰ ;    u 00 = ⁰ , ^О 0 r = ^{0 О} 0 z = °;

• -    отсутствие напряжений на поверхности 1: о _rr = 0, о r ₀ = 0, о _rz = 0 ;

• -    равенство нормальных напряжений на поверхности 2 нормальным (номинальным) напряжениям в нетронутом массиве и отсутствие на ней касательных напряжений: о rr = о * , где ct * =y ( H - у ); о r 0 = 0, о rz = 0;

• -    непрерывность перемещений на общей границе включения и среды;

• -    отсутствие перемещений выделенного для расчета фрагмента породного массива как абсолютно твердого тела; для этого полагается, что отсутствуют перемещения по оси у

• (uyy = 0) на нижней линии пересечения поверхности 2 с плоскостью zy и нулевое перемещение по оси z (uzz = 0 ) для одной из произвольных точек этой линии.

Расстояние поверхности 2 от оси выработки выбирается таким, чтобы перемещения этой поверхности, вызываемые проходкой, были пренебрежимо малы. Путем вычислительных экспериментов установлено, что это условие выполняется, если расстояние составляет примерно 100 м.

Численное решение поставленной задачи механики сплошной среды с физическими уравнениями (1), (2) отыскивается по алгоритму, приведенному в работе [9]. Отрезок интегрирования [0, t ] разбивается на n интервалов точками t 1 ,t 2 ,..., t_{n + 1}. Далее реализуется последовательность шагов по времени. Первый шаг отвечает мгновенному физически линейному нагружению ( t = t = 0 ); соответствующие физические уравнения (1), (2) имеют вид:

5, ( ⁰ ) = 2Gs , ( ° ) • 5 ( ⁰ ) = B К0) -® ' ].

На этом шаге решение получается методом конечных элементов с внутренними итерациями. На первой итерации считается, что соляная порода однородна и ее модуль упругости всюду имеет значение Е . В результате реализации первой итерации в расчетной области вблизи верхнего торца разгрузочной щели выявляются элементы, в которых интенсивность напряжений превышает значение ® сж . Такие элементы считаются разрушенными, и их модуль упругости заменяется на модуль материала включения — E ' . С новыми значениями упругих характеристик осуществляется вторая итерация, и так далее. Процесс повторяется до тех пор, пока в соляном массиве не будут выявлены все элементы, в которых интенсивность напряжений превышает значение ® сж . Вследствие перевода элементов массива в элементы щели ее длина увеличивается, разгрузочная щель продвигается вглубь массива. Таким образом, по окончании итерационного процесса на первом шаге по времени устанавливается такая длина щели, что условие прочности породного массива вблизи торца разгрузочной щели не нарушается (Рис. 2) и концентрация напряжений, способная вызвать разрушение в этой области, отсутствует.

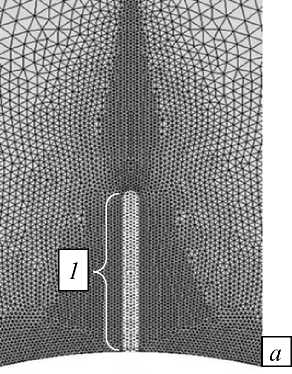
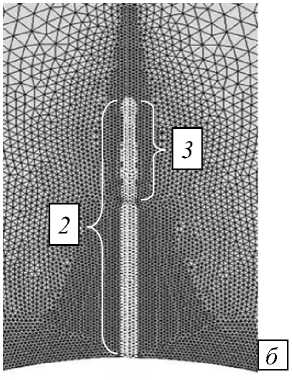
Рис. 2. Расчетная сетка в верхней части выработки с заполненной разгрузочной щелью перед началом ( а ) и по завершении итерационного процесса ( б ); 1 и 2 – исходная и окончательная длина разгрузочной щели;

3 – область расчетного удлинения щели за счет разрушенных элементов массива

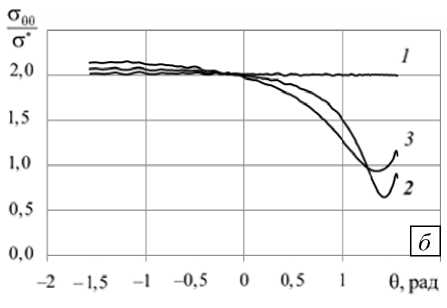
Поскольку параметры напряженно-деформированного состояния в породном массиве не изменяются вдоль оси выработки, на приведенных ниже рисунках демонстрируется их распределение в сечении плоскостью xy , в частности, в точках контура, получаемого при пересечении этой плоскости и поверхности выработки. На рисунке 3 показаны напряжения, возникающие при мгновенном нагружении массива без разгрузочной щели и с разгрузочной щелью различной длины. Видно, что и напряженное состояние, и протяженность области, в которой оно существенно отличается от напряженного состояния целостного массива, слабо зависят от длины щели. Данное заключение позволяет в дальнейшем не учитывать влияние увеличения длины разгрузочной щели на напряженно-деформированное состояние вблизи контура выработки при мгновенном нагружении.

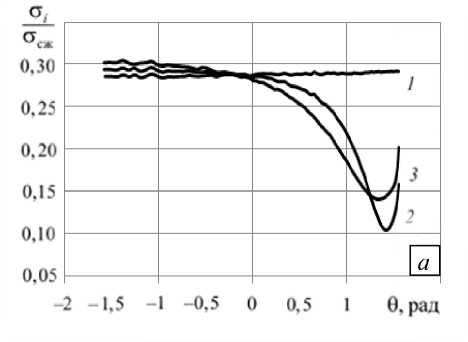
Рис. 3. Отношения ст i / ст сж ( а ) и ст_вв / ст * ( б) на контуре выработки при мгновенном нагружении массива без разгрузочной щели (кривая 1 ) и с разгрузочной щелью длиной 0,5 м ( 2 ) и 1,0 м ( 3 )

Изменение напряженно-деформированного состояния во времени находится далее из решения последовательности линейно-упругих задач с начальным напряженным состоянием [9]. В качестве начального состояния используется решение, полученное на предыдущем временном шаге. Для произвольного временного шага m + 1 физические уравнения имеют вид:

• 1                m

^ j ( t m + 1 ) =      s j ( t m + 1 ) — Е s ij ⁽ t k ^)[ П С ( t m + 1 — t k + 1 , ^СТ ( t k ) , ^CT i ( t k ) ) —

• ²    G            k = 1

— ^ПС ( t m + 1 — t k , ^CT ( t k ) , ^CT i ( t k ) ) ^] ,

^ tm + 1 ) =

B

^CT ( t m + 1 ) — ^CT

( m = 1,

n ) ,

где П_С ( t , ct ( t ) , ct i ( t ) ) — функция сдвиговой ползучести, устанавливаемая опытным путем.

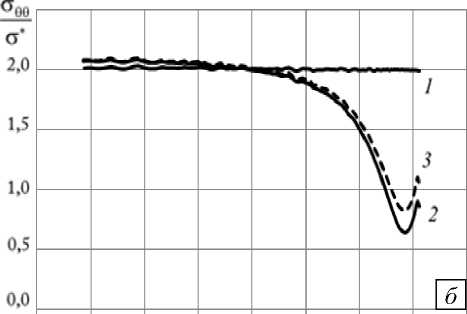
Результаты вычислений для выработки, залегающей на глубине Н = 200 м, представлены на рисунке 4. Из приведенных графиков видно, что разгрузочная щель вносит значительное изменение в напряженное состояние породного массива (вблизи контура выработки уровень напряжений понижается), и это изменение имеет не локальный характер, а наблюдается в области, которой отвечает центральный угол, превышающий значение п/3. На рассматриваемой глубине интенсивность напряжений удовлетворяет условию ст i <  0,4 ст _сж, поэтому соляная порода ведет себя как физически

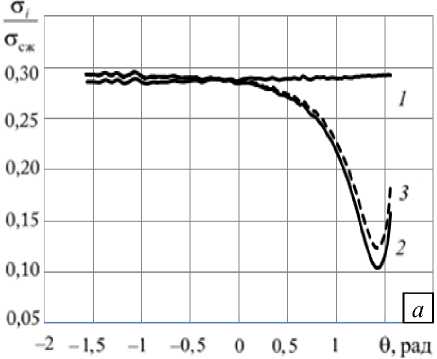
Рис. 4. Отношения а/а _сж ( а ) и о_вв / о * ( б) на контуре выработки без разгрузочной щели ( 1) и с разгрузочной щелью размерами l = 0,5 м, 5 = 0,04 м: в режимах мгновенного нагружения ( 2 ) и ползучести (предельные значения при t ^ю ) ( 3 )

-2 -1,5 -1 -0.5    0    0.5    1      0. рад

линейная среда. С течением времени напряжения, найденные с учетом ползучести, стремятся к предельным значениям (штриховая линия 3 на рисунке 4), которые также существенно ниже значений соответствующих характеристик для выработки без разгрузочной щели.

В связи с тем, что создание разгрузочной щели формирует в горном массиве довольно обширную область измененного напряженного состояния, появляется возможность управлять распределением напряжений посредством варьирования количества щелей. Для иллюстрации рассматривается выработка кругового сечения, залегающая на той же глубине ( Н = 200 м), с шестью одинаковыми разгрузочными щелями длиной l = 0,5 м и шириной 5 = 0,04 м . Поперечное сечение такой выработки приводится на рисунке 1, б . Расчет напряженно-деформированного состояния в массиве осуществляется так же, как и в рассмотренной выше задаче.

Представленные на рисунке 5 результаты вычислений свидетельствуют, что наличие шести разгрузочных щелей приводит к изменению напряженного состояния по всему контуру поперечного сечения выработки. При этом максимальные значения интенсивности напряжений уменьшаются примерно на 30% по сравнению со значениями в выработке без разгрузочных щелей, а окружное напряжение падает более чем в два раза и становится меньше номинального о * .

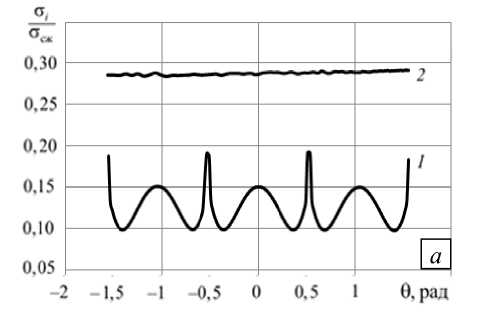
Рис. 5. Относительные интенсивность напряжений а i / а _сж ( а ) и окружное напряжение о_вв / о * ( б) на контуре выработки без щели ( 1 ) и с шестью разгрузочными щелями длиной l = 0,5 ( 2 ) при мгновенном нагружении

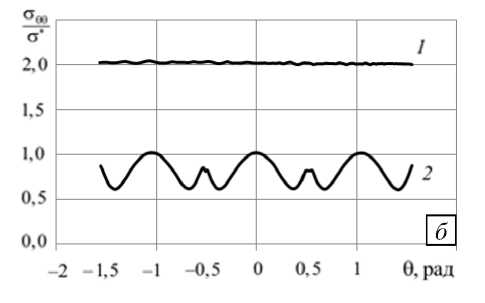
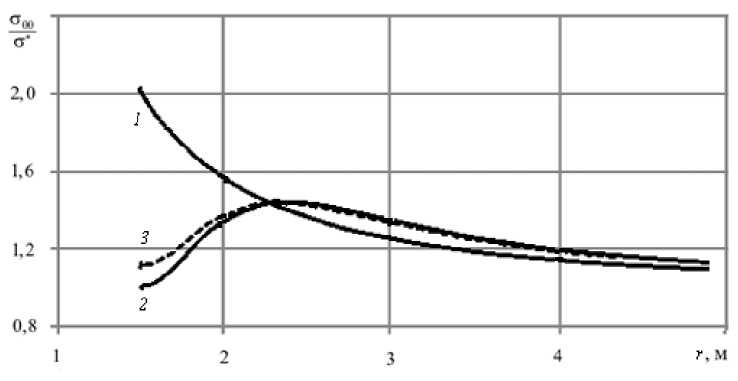
Рис. 6. Распределение σ_θθ σ^∗ в массиве в радиальном направлении (при θ = 0): в выработке без щелей ( 1 ) и с шестью разгрузочными щелями при мгновенном нагружении ( 2 ) и ползучести (при t →∞ ) ( 3 )

Изменение распределения окружного напряжения по мере удаления от стенок выработки, вызываемое наличием разгрузочных щелей, демонстрирует рисунок 6. При мгновенном нагружении породного массива (кривая 2 ) область максимальных значений окружных напряжений смещается вглубь на расстояние, примерно равное радиусу выработки. Величина максимального напряжения оказывается меньше величины напряжений на контуре выработки без разгрузочных щелей, то есть концентрация напряжений в окрестности выработки с разгрузочными щелями оказывается меньшей. С течением времени картина распределения напряжений σ _θθ в массиве меняется незначительно: они увеличиваются не более чем на 10% в непосредственной близости к контуру выработки.

Таким образом, благодаря использованию конечного числа разгрузочных щелей (в данном случае шести) удается существенно уменьшить уровень напряженного состояния (величину σ i ) вблизи контура выработки, снизить коэффициент концентрации окружных напряжений σ_θθ σ^∗ и отодвинуть зону повышенных значений этих напряжений от контура вглубь массива.

С увеличением глубины залегания выработки Н интенсивность напряжений вблизи ее стенок возрастает до значений σ _i > 0, 4 σ _сж , и массив переходит в состояние неограниченной ползучести. Для оценки влияния разгрузочных щелей в условиях неограниченной ползучести рассматриваются выработки, пройденные на глубине Н = 400 м. Динамика окружных напряжений на контуре для выработки с шестью разгрузочными щелями приводится на рисунке 7. С течением времени эти напряжения не релаксируют, а возрастают. Такое поведение можно объяснить тем, что вследствие ползучести разгрузочные щели стремятся «закрыться», а окружные напряжения — восстановить значения, отвечающие состоянию круговой выработки без разгрузочных щелей.

С течением времени коэффициент концентрации напряжений остается значительно меньшим, чем в выработке без щелей. Кроме того, уменьшается разность значений напряжения σ _θθ в соседних точках контура, кривая σ_θθ / σ ^* «выполаживается» (см. кривую 3 , Рис. 7)

Рисунок 8 показывает, каким образом ползучесть проявляется на контуре выработки при различном числе разгрузочных щелей. Видно, что радиальные перемещения u_r точек контура выработки по направлению к ее центру минимальны для выработки без разгрузочных щелей. С увеличением количества щелей ползучесть контура выработки возрастает.

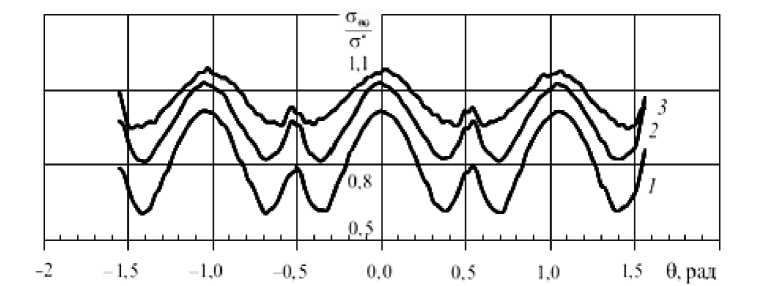
Рис. 7. Отношение ст ₉₉/ ст * на контуре выработки: при мгновенном нагружении ( 1 ); через восемь ( 2 ) и 30 суток ( 3 ) от момента нагружения

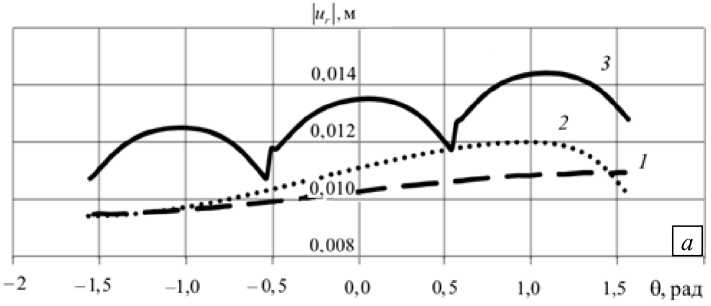
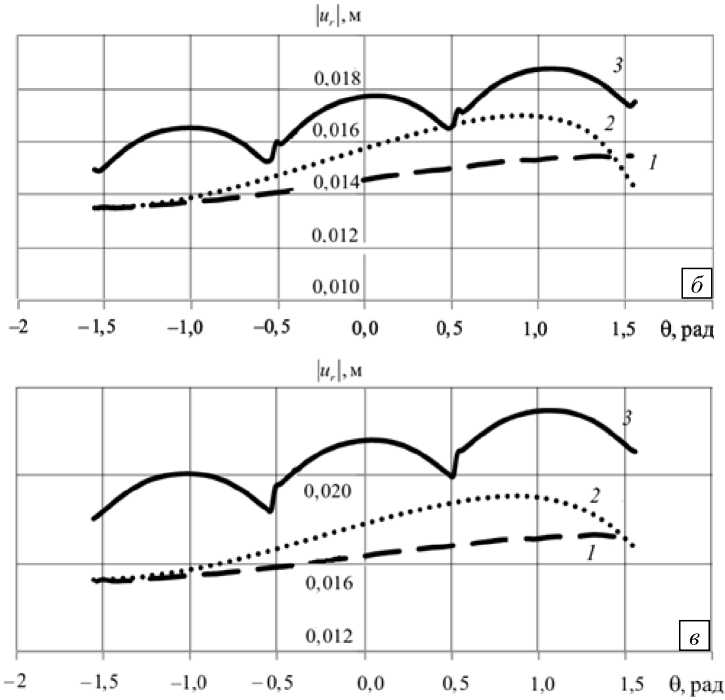
Рис. 8. Ползучесть контура выработки в зависимости от количества разгрузочных щелей: мгновенное нагружение ( а ); одни сутки ( б); 30 суток ( в ); 1 - без щелей; 2 - одна щель; 3 - шесть щелей

Выводы

• 1.    Разгрузочная щель, ортогональная стенкам выработки, существенно изменяет напряженное состояние в примыкающем массиве, и это изменение носит нелокальный характер .

• 2.    Использование конечного числа разгрузочных щелей позволяет значительно уменьшить интенсивность напряжений в окрестности выработки, снизить концентрацию окружных напряжений, отодвинуть зону повышенных значений этих напряжений от контура выработки вглубь массива.

• 3.    Окружные напряжения на контуре выработки с разгрузочными щелями с течением времени возрастают, оставаясь по величине значительно меньше значений, соответствующих выработке без щелей ( ≈ 2 σ ^* ).

• 4.    Отрицательное влияние разгрузочных щелей проявляется в том, что в вязкоупругом породном массиве они приводят к возрастанию ползучести стенок выработки по направлению к ее центру.