Влияние различных факторов на здоровье населения

Основная трудность статистического анализа влияния множества факторов на некоторый интересующий исследователя показатель (отклик) состоит в том, что статистическая связь, выявляемая с помощью регрессионного или корреляционного анализа, не обязательно соответствует причинной связи. Если имеется статистическая связь (корреляция) отклика с двумя коррелированными между собой факторами, то в рамках анализа невозможно определить, какой из двух факторов является причиной. Более того, причиной может быть какой-то третий фактор, данные о котором могут отсутствовать в результатах обследования, но с которым статистически связаны обследованные факторы.

В качестве примера рассмотрим следующую модельную ситуацию. Пусть имеется некоторый причинный фактор A , принимающий значения от 1 до 50, который влияет на отклик R . Допустим, что это влияние описывается регрессионным уравнением R = A + error , где error – случайная ошибка измерения. Пусть также имеются два других фактора B и C , статистически связанных

Римашевская Н.М. и др.

с A аналогичными регрессионными уравнениями: B = A + error и C = A + error .

Проведенные нами тестовые расчеты при различных случайных ошибках показывают, что корреляция R с причинным фактором A устойчиво выше, чем с сопутствующими факторами B и C (что естественно, поскольку B и C содержат неточную информацию об A ). Типичный пример из проведенных расчетов: корреляция R с A равна 0,71, а с B и C – 0,52 и 0,54 соответственно.

Множественный регрессионный анализ R по A , B и C также выделяет фактор A в качестве наиболее значимого. Например, в одном из расчетов при уровне значимости A , равном p =0,0002, уровни значимости факторов B и C составляли соответственно p =0,58 и 0,51, т.е. статистически незначимы.

Однако множественный регрессионный анализ R только по B и C давал в разных расчетах противоречивые результаты. Одни результаты, в которых оба уровня значимости факторов B и C были значимы (например, p =0,001 и 0,04). В других – значимым был фактор B (например, p =0,002 и 0,60), в третьих – фактор C (например, p =0,16 и 0,003).

Такого рода модельные расчеты и теоретические соображения позволяют предложить следующую методику выявления структуры зависимости отклика от набора факторов. Выделяем фактор, наиболее коррелированный с откликом. Если содержательно он может быть принят в качестве причинного фактора, то строим регрессию отклика по этому фактору – назовем его «первым» – и находим остатки от регрессии – назовем их «первыми». Первые остатки характеризуют отклик при исключенном влиянии первого фактора. На следующем этапе выделяем фактор, наиболее коррелированный с первыми остатками. Если содержательно он может быть принят в качестве второго причинного фактора, то строим множественную регрессию отклика по двум причинным факторам и находим остатки от этой регрессии – назовем их «вторыми». Вторые остатки характеризуют отклик при исключенном влиянии первого и второго факторов. Процедура продолжается до тех пор, пока корреляции очередных остатков со всеми оставшимися факторами не станут незначимыми.

Данная методика была применена к выявлению структуры зависимости самооценок здоровья респондентов от различных факторов по данным анкетного обследования москвичей 2004 г. ¹

Наибольшую корреляцию с оценкой здоровья имел фактор возраста ( r = 0,43, p < 0,000001). Уравнение регрессии оценки здоровья (в баллах от 1 до 5) от возраста (в годах) имеет вид:

Оценка здоровья =

= 4,0 – 0,02 х Возраст

Вычисленные для каждого респондента по этому уравнению расчетные оценки здоровья были вычтены из анкетных оценок, и полученные значения образовали набор «первых остатков» – оценок здоровья при исключенном влиянии возраста.

Затем были вычислены корреляции первых остатков со всеми факторами (кроме, разумеется, возраста, корреляция с которым по построению остатков должна была быть равна нулю). Наибольшие значения имели корреляции оценок здоровья при исключенном влиянии возраста со следующими двумя факторами: с неудовлетворенно-

Здоровье населения

стью жизнью (вопрос 70 – шкала от 1 до 4, r = -0,29, p < 0,000001) и оценкой материального положения семьи (шкала от 1 до 5, r = 0,28, p < 0,000001).

Более бесспорным вторым (после возраста) причинным фактором представляется материальное положение семьи – в силу своей большей объективности (показатель неудовлетворенности жизнью может неявно включать неудовлетворенность состоянием здоровья). Поэтому сначала мы проанализируем этот фактор, построив регрессию оценки здоровья от возраста и материального положения семьи:

Оценка здоровья =

= 3,2 – 0,017 х Возраст +

+ 0,26 х Материальное положение (множественный коэффициент корреляции равен 0,50, уровень значимости меньше 0,000001).

Мы видим, что вклады этих двух факторов в оценку здоровья, принимая во внимание диапазоны их изменения, соизмеримы и противоположны: уменьшение оценки материального положения семьи на один балл равноценно увеличению возраста примерно на 15 лет.

Найдем теперь остатки от полученной регрессии и вычислим корреляции остатков со всеми факторами. Влияние подавляющего большинства факторов оказывается статистически незначимым и не превосходит по абсолютной величине значения 0,1, а с учетом поправки Бонферрони они практически все незначимы. Это позволяет говорить о том, что основными факторами, определяющими оценки здоровья, являются возраст и оценка материального положения семьи. Степень же незави-

18000 ф

15000 о

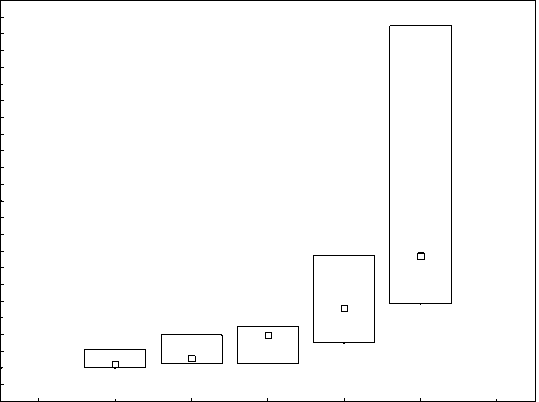
Балльная оценка материального положения семьи

Внутренние квадратики соответствуют медианам расходов, внешние прямоугольники – интерквартильной широте

Рис. 1. Связь суммы месячного расхода на одного члена семьи (в тыс. руб.) с балльной оценкой материального положения семьи.

Римашевская Н.М. и др.

симого влияния каких-либо других, менее значимых факторов, по имеющемуся материалу достоверно установить не удается (в силу наличия случайных ошибок измерения).

В нашем расчете фактором, наиболее связанным с оценкой здоровья (после исключения эффекта возраста), оказалась балльная оценка материального положения семьи. На рис. 1 эта оценка сопоставляется с месячной суммой расходов на одного члена семьи.

Мы видим, что в денежном выражении баллы материального положения семьи неравноценны. Так, для перехода от балла 1 (очень плохое материальное положение семьи) к баллу 2 (просто плохое) достаточно повысить медианный месячный расход на члена семьи всего на 500 руб. – примерно от 2000 до 2500 (а это равноценно омоложению на 15 лет по балльной оценке здоровья!). Повышение материального положения се- мьи еще на один балл – от плохого к удовлетворительному – соответствует повышению месячного расхода на члена семьи от 2500 до 4000 руб., т.е. на 1500 руб. Повышение еще на один шаг – от удовлетворительного к хорошему – обходится еще в 1500 руб. (повышение от 4000 до 5500 руб.). И, наконец, последний шаг – повышение материального положения семьи от хорошего к отличному для половины людей требует увеличения месячного расхода на члена семьи не более чем на 3250 руб. – от 5500 до 8750 руб.

В этой связи следует отметить, во-первых, относительно скромные запросы большинства респондентов, а во-вторых – совсем небольшие запросы наименее обеспеченных.

Это означает, что с точки зрения увеличения суммарного здоровья населения наиболее эффективны вложения в повышение уровня жизни беднейших слоев.