Влияние реологических свойств крови на формирование рециркуляционных зон вблизи стеноза коронарной артерии

RUSSIAN JOURNAL OF BIOMECHANICS

Большая часть фундаментальных работ по гемодинамике посвящена вопросу об атеросклеротических поражениях, поскольку сердечно-сосудистые заболева- ния – одна из основных причин смертности населения в большинстве стран мира [1; 2]. Атеросклероз – хроническое и прогрессирующие заболевание, сопровождающееся формированием атеросклеротической бляшки [3]. Бляшка уменьшает просвет сосуда, вызы-

Современные научные предположения о влиянии биомеханических факторов на развитие атеросклероза, основываются частично на клинических наблюдениях, что атеросклеротические поражения преимущественно возникают у устьев ветвящихся сосудов, в сегментах артерий с высокой кривизной или в местах с резко меняющейся геометрией, где могут наблюдаться серьезные изменения в структуре кровотока [4–9]. Изменения кровотока негативно воздействуют на работу сердечно-сосудистой системы, приводят к деформации вая серьезные изменения в структуре кровотока, что

может приводить к формированию стеноза.

артерий, что в конечном счете меняет локальные рео-

логические свойства крови.

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

Мнение о существовании вихревых зон в сложной структуре коронарной артерии не было широко распространено. Однако для полностью развитого стационарного ламинарного течения вязкой несжимаемой жидкости возможно формирование стационарных зон из-за процесса, известного как отрыв пограничного слоя [10; 11]. Впоследствии было обнаружено сходство между областями, где происходит отрыв, и местами, склонными к развитию атеросклероза [12]. Классическая концепция отрыва потока связана с вязкостными свойствами среды. Необходимым условием возникновения устойчивого обратного течения и дальнейшего формирования стационарной вихревой зоны является наличие положительного градиента давления в направлении течения жидкости. Такая низкоскоростная зона характеризуется малыми сдвиговыми скоростями и напряжениями в пристеночной области сосуда. Большинство теоретических и экспериментальных работ посвящены изучению локальной гемодинамики в области стеноза [13-22].

Вычислительная гидродинамика (ВГД) считается одним из основных подходов в моделировании сложных течений, в частности, в биомедицинском моделировании [13–16]. Компьютерное моделирование кровотока требует использование наиболее точных вязкостных моделей, которые достоверно отразят его уникальные реологические свойства. Результаты исследований коронарной гемодинамики с помощью ВГД находят применение в клинической практике [23].

Вблизи стеноза развиваются сложные пространственные течения, которые затруднительно проанализировать, поэтому во многих работах авторы сравнивают однопараметрические и многопараметрические модели с целью определить их надежность и адекватность полученных результатов при сравнении с данными клинических исследований. В [13] проводилось сравнение 16 реологических моделей как между собой, так и с данными, полученными in vivo . Было показано, что профили скорости, полученные с помощью трех реологических моделей, включая модель Каро, давали наиболее близкие результаты к измеренным in vivo . Сделан вывод, что моделирование, выполненное с использованием других моделей, может привести к различиям в результатах напряжения сдвига стенки и скорости, достигающим 60 %, с данными in vivo . Была продемонстрирована взаимосвязь между скоростью кровотока и перепадами давления.

Установлено, что сдвиговое напряжение стенки играет значительную роль среди биомеханических факторов [4]. Подробная оценка его пространственного распределения может дать ключевую информацию для понимания развития атеросклероза. В [24] показано, что вязкостные свойства крови качественно влияют на напряжение сдвига в областях с нарушенным кровотоком, а ньютоновская модель и модель Каро демонстрируют хорошее количественное соответствие.

Как и в других работах [25-27], отмечается, что, в зависимости от входной скорости, модель Каро и ньютоновская могут давать либо заниженные, либо завышенные результаты для сдвигового напряжения.

Несмотря на возможную причинно-следственную связь между процессом отрыва пограничного слоя и развития атеросклероза, немногие работы посвящены изучению особенностей рециркуляционных областей [28-30]. В одной из таких работ [6] проведены численные расчеты для модели с двойным стенозом. При исследовании характеристик рециркуляционных зон было подчеркнуто, что сила вихря по часовой стрелке была выше, чем против часовой. Наличие подобных областей в большей степени наблюдалось для ньютоновской модели, где течение было полностью развито.

Условиями, которые могут привести к формированию стабильно расположенных рециркуляционных зон, будут локально сниженная скорость и повышенная вязкость кровотока. Следует подчеркнуть, что вязкостные свойства крови являются главным фактором, который принципиально влияет на динамику кровотока, вследствие чего имеет патологическое значение.

Настоящее исследование посвящено влиянию реологических свойств крови на формирование рециркуляционных зон в гемодинамических течениях вблизи стеноза коронарной артерии. В качестве реологической модели выбрана широко используемая для описания коронарной гемодинамики модель Каро, которая учитывает неньютоновские свойства крови. На примере 2 D -моделей с двойным и одиночным стенозом было численно исследовано явление отрыва пограничного слоя и показан потенциальный вклад реологических свойств крови в локальную гемодинамику кровотока. Чтобы продемонстрировать практическую значимость полученных результатов, были проведены аналогичные расчеты на примере 3 D- модели реальной коронарной артерии, реконструированной по данным рентгеноконтрастной коронарографии. Чтобы показать вклад реологических свойств крови в особенности формирования рециркуляционных зон, вязкость, перепады давления, напряжения сдвига стенки и сдвиговые скорости в области стеноза, сравнивались результаты с расчетами для ньютоновской модели крови.

Материалы и методы

Гемодинамическая модель

Рассматривалось ламинарное течение сплошной несжимаемой среды в приближении динамики крови в артерии. Моделирование выполнено путем численного решения уравнений Навье - Стокса:

W = 0,

Р + Р ( V V) V = -V P + V T , д t

T eff = И [2 S - 2 (V V ) I j i {dK дV j

S ^ S j =--^l- + — j

1   2 [ 5Xj   дxi где V - вектор скорости, p - плотность, P - давление, tef - тензор вязких напряжений, ц - коэффициент ди намической вязкости, S - тензор скоростей деформации, I - единичный тензор. В силу нелинейной зависимости динамической вязкости от скорости сдвига, кровь можно рассматривать как неньютоновскую жидкость и описывать различными реологическими моделями. В настоящей работе использовалась модель Каро, которая успешно применяется при моделировании гемодинамики [6; 31; 32]. Уравнение Каро для ц имеет следующий вид:

n –1

И=И min ⁺ ( И тах ^- И min )(¹⁺^ S ) 2

^Ц min — ^Ц — ^Ц max ,

S=2ХS2, ij

^X = V^ц max ^/t ’

где umin , l„ - минимальное и максимальное значе-min    max ние динамической вязкости, X - коэффициент релаксации, S - модуль обобщенного градиента скорости, *

n - эмпирическая постоянная, т - характеристическое напряжение сдвига. При рассмотрении крови как ньютоновской жидкости использовалась константа μ=μ _min . Параметры для реологической модели представлены в табл. 1.

Дизайн и алгоритм моделирования

На рис. 1 представлена схема вычислительной области, используемой для двумерной задачи. Граничному условию слева соответствовала скорость Vin =0,35; 0,5 м/с, направленная по нормали к границе. На границе справа задано условие нулевого градиента статистического давления P . Верхняя граница рассматривалась как жесткая стенка с условием прилипания, нижняя граница - как жесткая стенка без условия прилипания. Такой подход является распространенным способом решения для ламинарных течений в осесимметричных задачах. Форма стеноза определялась следующим выражением:

A= 1 – ^Rst R²

и соответствовала стенозу с перекрытием A = 0,5 .

На рис. 2 представлена трехмерная аксиально-симметричная модель, построенная по результатам рентгеноконтрастного исследования [17] и используемая для моделирования гемодинамики в реальной коронарной артерии. Площадь сужения составляла 50 %.

Входному граничному условию соответствовала скорость V _in =0,35; 0,5 м/с, направленная по нормали к поверхности. На выходе было задано условие нулевого градиента статистического давления P . Граница рассматривалась как жесткая стенка с условием прилипания.

Для каждой представленной модели были проведены тестовые расчеты на сходимость сетки, результаты которых представлены на рис. 3.

Видно, что давление перестает зависеть от размера ячейки при N = 108 тыс. (рис. 3, а ) и при N = 450 тыс. (рис. 3, б ). Дальнейшее увеличение размера ячеек не повлияло на изменение параметра. Выбранная сетка позволила ограничить вычислительные затраты и получить достоверные результаты.

Для решения уравнений (1)–(2) использовался метод конечных объемов для регулярной шестигранной сетки, реализованный в программном комплексе ВГД FlowVision [33].

Результаты

2D-модель с двойным стенозом

Результаты моделирования тока крови вблизи стеноза при фиксированных скоростях потока для реологической модели Каро и для модели с постоянной вязкостью представлены на рис. 4, 5.

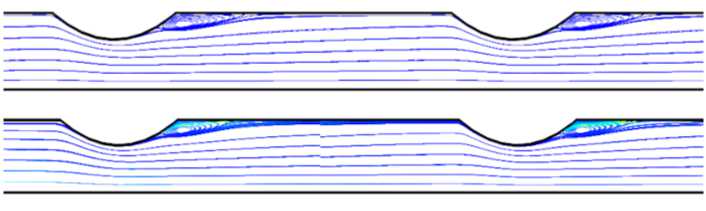
Ламинарный поток был описан с помощью отображения контуров линий тока. При рассмотрении стационарных течений линии тока совпадают с траекторией движения жидкой частицы в среде, поэтому очень часто они используются для отображения направления жидкости и обнаружения возмущений в потоке. Результаты представляют собой потоки с четко выраженными стационарными зонами рециркуляции, что свидетельствует о наличии ретроградного кровотока. Отметим, что для любой скорости потока реологические свойства крови обусловливают увеличение вязкости в вихревой зоне. При малых скоростях вязкость выше в среднем на 29 % (рис. 4). Качественно это отражается в уменьшении размеров вихря.

Результаты моделирования для давления вдоль сосуда представлены на рис. 6.

Наблюдаемое падение давления обусловлено наличием стеноза. Перепады давления связаны в первую очередь с увеличением продольной компоненты скорости в области стеноза, что объясняется уравнением Бернулли и уравнением неразрывности. Обе модели дают ы для модели

Параметр	Значение	Единицы измерения
ρ	1055	кг/м 3
n	0,3568	–
λ	3,131	с
μ min	0,004	Па∙с
μ max	0,056	Па∙с

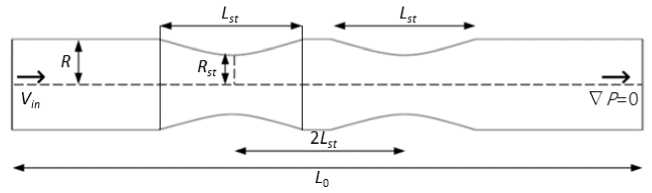
Рис. 1. Схема моделируемого сосуда с двойным стенозом. Исходя из симметричности моделируемой области, рассматривается только верхняя половина сосуда. В работе рассматривается L ₀ = 50 мм, L _st =5 мм, R = 1,25 мм

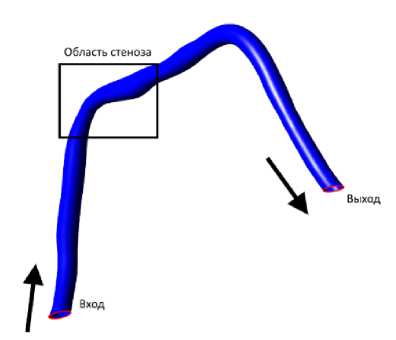
Рис. 2. Фрагмент коронарной артерии со стенозом, реконструированный по данным рентгеноконтрастной коронарографии. Стрелками показаны граничные условия

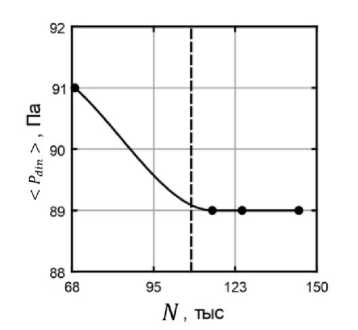
а

Рис. 3. Зависимость среднего динамического давления P din от количества ячеек в расчетной сетке N : а – 2 D -модель; б – 3 D -модель. Пунктирная линия соответствует количеству ячеек N в выбранной сетке

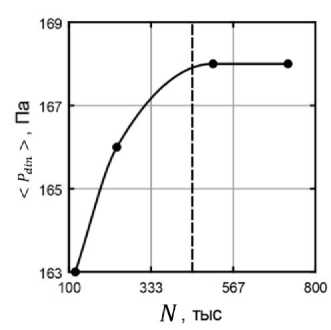
б

Вязкость, мПа*с

Рис. 4. Результаты моделирования при скорости потока 0,35 м/с. Верхняя панель: ньютоновская модель; нижняя панель: модель Каро. Линии отражают ток крови в плоскости.

Распределение вязкости представлено в цветовой гамме

4 4,4 4,7 5,1 5,5 5,9 6,4 6,9 7,5 8,1 8,7

Вязкость, мПа'с

Рис. 5. Результаты моделирования при скорости потока 0,5 м/с. Верхняя панель: ньютоновская модель; нижняя панель: модель Каро. Линии отражают ток крови в плоскости.

Распределение вязкости представлено в цветовой гамме го

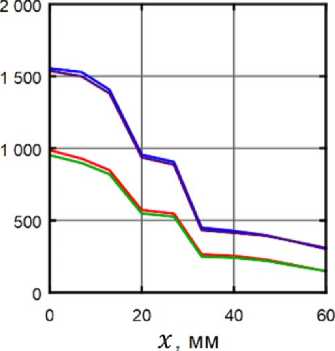
Рис. 6. Зависимость давления P от координаты вдоль сосуда x . Зеленая кривая – ньютоновская модель, V _in = 0,35 м/с; красная кривая – модель Каро, V _in = 0,35 м/с; сиреневая кривая – ньютоновская модель, V _in = 0, 5 м/с; синяя кривая – модель Каро, V _in = 0, 5 м/с

практически одинаковые результаты, особенно при высоких скоростях потока.

2 D-модель с одиночным стенозом

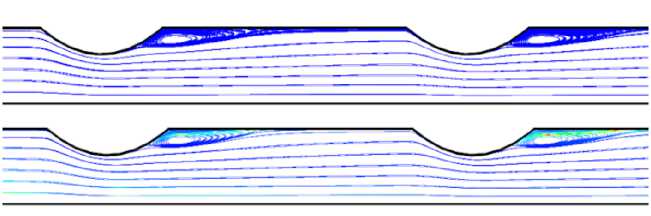
В качестве дополнительного исследования была рассмотрена 2D-модель идеального сосуда с разными уровнями стеноза (65 %, 80 %). При постановке задачи использовались аналогичные уравнения гидродинамики и граничные условия, рассмотренные при исследовании модели с двойным стенозом. Результаты моделирования представлены на рис. 7, 8.

При увеличении области стеноза наблюдается значительное удлинение вихревых зон. Из результатов

Рассчитанная площадь рециркуляционной области вблизи стеноза

Модель Уровень стеноза, % Площадь зоны рециркуляции, мм2 Модель Каро 65 4,32 80 17,792 Ньютоновская модель 65 4,185 80 16,2 можно видеть, что в случаи критических стенозов площадь рециркуляционной области может доходить до 17 мм2 (табл. 2). Однако существенного отличия по результатам между моделью Каро и ньютоновской моделью не выявлено. С другой стороны, в этой области также наблюдается увеличение вязкости.

Также было рассмотрено давление вдоль сосуда (рис. 9).

Аналогичное поведение давления характерно и для сосудов с одиночным стенозом. Резкий спад давления на графике характерен для области стеноза. При этом разница между значениями до и после стеноза для модели с перекрытием 80 % выше в 2 раза, что является закономерным следствием уравнения Бернулли.

3D-модель

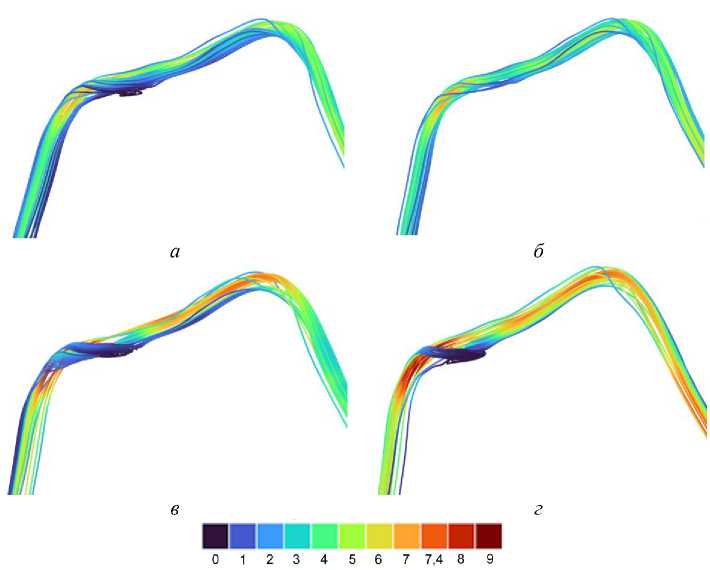
Результаты моделирования тока крови вблизи стеноза при фиксированных скоростях потока для реологической модели Каро и для модели с постоянной вязкостью представлены на рис. 10, 11.

Более низкие скорости в застойной зоне характерны для моделей с меньшей скоростью на входной границе. При малых скоростях потока в модели Каро вихрь не развивается вовсе (рис. 11, б ), тогда как ньютоновская модель при любых скоростях дает решение с рециркуляцией тока (рис. 11, а, в ).

Важно отметить увеличение вязкости в области формирования вихря. В целом увеличение в силу реологических свойств крови в зоне рециркуляции составило 58 % по сравнению с ньютоновской моделью. Это обстоятельство является следствием уравнения Каро (2), которое использовалось при описании неньютоновской жидкости.

Были рассчитаны средние сдвиговые скорости в области стеноза для обеих моделей (табл. 3).

Более высокие значения характерны для скорости потока 0,5 м/с для обеих моделей. Полученные значения согласуются с данными литературы в случае некритичных стенозов. Наибольшая разница в значениях проявляется при высоких скоростях потока, из чего можно утверждать, что при низких скоростях модели ведут себя одинаково.

Результаты для среднего динамического давления вблизи стеноза представлены в табл. 4.

В области после сужения, где формируется вихревая зона, наблюдается снижение давления. Более высокие перепады характерны преимущественно для моделей с высокой скоростью потока, тогда как с низкой скоростью разница практически отсутствует. Можно отметить, что градиент давления коррелирует с перепадами скорости, которые возникают до и после сужения. Наибольшая разница в перепадах давления наблюдается в области стеноза и в области рециркуляции.

Представлена зависимость среднего напряжения сдвига в пристеночной области стеноза от расчетного времени (рис. 12, 13). Максимальное напряжение сдвига зафиксировано непосредственно в сужении вблизи поверхности сосуда и в целом распределено в пристеночной области неоднородно.

По результатам расчета можно отметить явный скачок сдвигового напряжения у ньютоновской модели и его отсутствие у модели Каро. Предполагается, что в ньютоновской модели по мере продвижения фронта потока в пристеночной области увеличивается сдвиговая скорость, следовательно, и сдвиговое напряжение в силу линейной зависимости. В модели Каро рост напряжения сдвига уравновешивается уменьшением вязкости. В среднем более высокие значения напряжения сдвига характерны для модели Каро при любых входных скоростях.

Обсуждение

Из-за важности атеросклеротического поражения все больше внимания уделяется компьютерному моделированию и ВГД как определяющему подходу в оценке коронарной гемодинамики. Вследствие чего необходимо критически оценивать точность моделирования кровотока. В большинстве моделей вязкость крови считается постоянной (примерно 4 мПа∙с), так как принято, что для крови свойственно ньютоновское поведение. Однако в сложных геометриях, где наблюдаются серьезные нарушения потока: области рециркуляции, пульсации, турбулентность, кровь начинает проявлять неньютоновские свойства, в связи с чем возникает необходимость применения реологических моделей.

В работе рассматривалось несколько двумерных геометрий со стенозом разной степени перекрытия сосуда и геометрия со множественным стенозом. Результаты работы подтверждают устойчивое формирование областей вихреобразования непосредственно за стенозом, в том числе для подряд расположенных стенозов (двойных стенозов). Это позволяет перейти к упрощению модельной задачи и исследованию одиночных стенозов без ограничения общности.

3,5 4,1 4,6 5,1 5,7 6,2 6,7 7,2 7,8 8,3 8,8

Вязкость, мПа*с

Рис. 7. Результаты моделирования для стеноза с перекрытием 65 % при скорости потока 0,5 м/с. Верхняя панель: ньютоновская модель; нижняя панель: модель Каро. Линии отражают ток крови в плоскости. Распределение вязкости представлено в цветовой гамме

3,5 3,9 4,3 4,6 5 5,4 5,7 6,1 6,5 6,8 72

Вязкость, мПа*с

Рис. 8. Результаты моделирования для стеноза с перекрытием 80 % при скорости потока 0,5 м/с. Верхняя панель: ньютоновская модель; нижняя панель: модель Каро. Линии отражают ток крови в плоскости. Распределение вязкости представлено в цветовой гамме

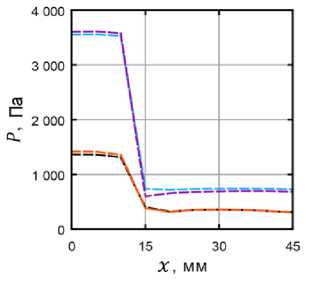
Рис. 9. Зависимость давления P от координаты вдоль сосуда x . Оранжевая кривая – ньютоновская модель, уровень стеноза – 65 %; черная кривая – модель Каро, уровень стеноза – 65 %; фиолетовая кривая – ньютоновская модель, уровень стеноза – 80 %; голубая кривая – модель Каро, уровень стеноза – 80 %

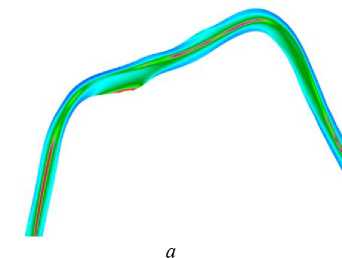
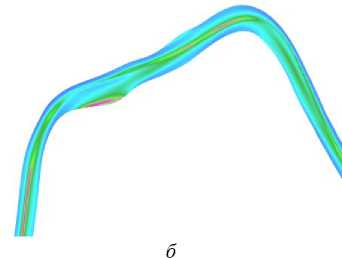
4 4,4 4,9 5,3 5,8 6,2 6,7 7,1 7,6 8 8,5 Вязкость. мПа‘с

Рис. 10. Результаты моделирования при скорости потока: а – 0,35 м/с; б – 0,5 м/с. Распределение вязкости представлено для модели Каро

Значения средних сдвиговых скоростей в области стеноза

Модель	Скорость, м/с	Скорость сдвига, 1/с
Модель Каро	0,35	308
	0,5	483
Ньютоновская модель	0,35	306
	0,5	397

СКОрОСТЬх1 о ’ м/с

Рис. 11. Результаты моделирования при скорости потока: верхняя панель – 0,35 м/с, нижняя панель – 0,5 м/с: а , в – ньютоновская модель; б , г – модель Каро. Линии отражают ток крови в пространстве (цвет линий соответствует модулю скорости)

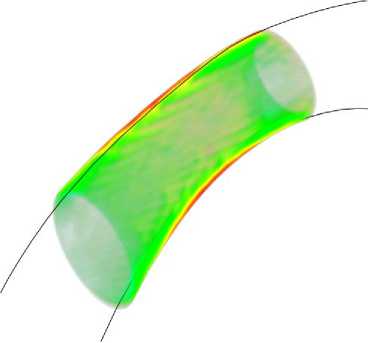
Рис. 12. Фрагмент коронарной артерии со стенозом. Цвет пристеночной области стеноза соответствует напряжению сдвига вдоль стенки сосуда

О 2   5   7   9 11 14 16 15 20 23

Напряжение сдвига, Па

Значения среднего динамического давления для разных областей вблизи стеноза

Модель	Скорость, м/с	До стеноза	В области стеноза	После стеноза
Модель Каро	0,35	33,5	100,3	35,2
	0,5	64,9	200,2	72,3
Ньютоновская модель	0,35	32	99,7	35,2
	0,5	64,9	201,7	74,2

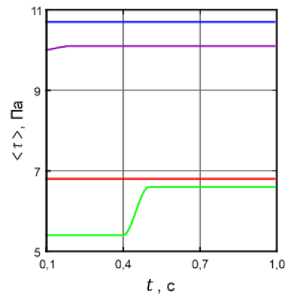
Рис. 13. Зависимость среднего сдвигового напряжения τ от времени расчета t .

Зеленая кривая – ньютоновская модель, V _in = 0,35 м/с; красная кривая – модель Каро, V _in = 0,35 м/с;

фиолетовая кривая – ньютоновская модель, V _in

0, 5 м/с; синяя кривая – модель Каро, V _in = 0, 5 м/с

На примере простой двумерной модели со множественным стенозом с помощью математического моделирования также обосновано формирование рециркуляционных зон после сужения и показано, что учет реологических свойств крови влияет на особенности этих областей, в частности на их размеры. Следует отметить, что увеличение вязкости в зоне вихря неоднородно, а преимущественно наблюдается вблизи верхней стенки. Это влечет за собой неравномерное распределение скоростей между слоями жидкости [31].

Исследование 2 D -модели сосуда с одиночным стенозом показало, что в случае более серьезных перекрытий сосуда возможно существенное удлинение вихреобразных областей. Однако при любых скоростях потока величина площади подобных зон незначительно зависит от реологических свойств крови. Следует отметить также увеличение вязкости в данной области. Из чего можно заключить, что, к примеру, для прогнозирования тромбо-образования следует использовать модель Каро, которая позволяет оценить изменение вязкости крови.

Для того чтобы подчеркнуть практическую значимость результатов были проведены эти же расчеты для трехмерной модели реальной коронарной артерии. Распределение вязкости в вихревой зоне совпадает по распределению для двумерной модели, т. е. максимальные значения наблюдаются преимущественно у стенки сосуда. При малых скоростях потока модель Каро не обеспечивает развитие вихря, в отличие от ньютоновской модели крови. Принципиально это связано с локальным изменением динамической вязкости. Данный результат может являться критерием гемодинамической значимости стеноза и последующей реканализации стенотических артерий.

Сдвиговое напряжение и скорость являются важными факторами, на которые обычно обращают внимание в работах [4]. При малых скоростях потока ньютоновская модель и модель Каро дают заниженные значения напряжения сдвига, тогда как при высоких скоростях разница практически отсутствует. Подчеркнем наличие явного скачка напряжения сдвига для ньютоновской модели при малой скорости. Можно предположить, что при высоких значениях скорости для описания напряжения сдвига может быть использована как модель Каро, так и ньютоновская модель.

Необходимо подчеркнуть, что в литературе практически не уделяют внимание расчету и анализу сдвиговых скоростей непосредственно в области стеноза и в зонах рециркуляции. В настоящей работе показано, что заметная разница между результатами при использовании модели Каро и ньютоновской модели проявляется при больших скоростях течения. Можно сделать вывод, что для более детального описания стенотической области необходимо использовать модель Каро и другие реологические модели.

Заключение

Рассмотрено влияние реологических свойств крови на особенности вихреобразования вблизи стеноза. Использована модель Каро для описания динамической вязкости и проведено сравнение результатов с ньютоновской моделью. На примере двумерных моделей прямого сосуда было обосновано физическое явление отрыва потока и показана взаимосвязь между реологическими свойствами крови и характеристиками явления рециркуляции потока вблизи стеноза. Была использована трехмерная модель реальной коронарной артерии, чтобы продемонстрировать особенности рециркуляционных областей на примере сложной геометрии реального сосуда. Сравнение результатов, полученных с ньютоновской моделью и моделью Каро, показало количественную и качественную разницу, основной причиной которой является проявление кровью неньютоновского поведения. Независимо от используемой геометрии сосуда, наблюдаемая вязкость в области вихря всегда выше, чем в остальном сосуде.

Ньютоновская модель крови не может учитывать локальные изменения динамической вязкости в областях вихреобразования, поскольку линейно зависит от