Влияние сферичности земной поверхности на управление ориентацией космического аппарата дистанционного зондирования Земли

Дистанционное зондирование Земли (ДЗЗ) является одной из важнейших задач космической отрасли, которая в настоящее время приобрела жизненно необходимый характер. Наиболее распространенным способом нацеливания космического аппарата (КА) на объект земной поверхности является использование двигателей малой тяги, применение которых предполагает расход топлива, что ограничивает количество переориентаций, а, следовательно, и наблюдений. Одним из вариантов, позволяющих избежать проблемы расхода рабочего тела, является применение электрических двигателей-маховиков [1]. Кроме того, отсутствие запаса топлива на борту КА подразумевает уменьшение его рабочей массы, что позволяет установить более качественную оптическую аппаратуру.

Движение систем, содержащих массивные вращающиеся элементы, изучали многие отечественные и зарубежные исследователи, результаты которых приведены, например, в [2-11]. Основным направлением их исследований была устойчивость движения при наличии различных динамических возмущений. Относительно малое число работ содержит конкретные рекомендации по управлению системой для обеспечения некоторого заданного движения.

В настоящей работе производится попытка решения конкретной прикладной задачи: определения законов управления ориентацией КА ДЗЗ с частичной закруткой при движении по круговой орбите для наблюдения за объектом, заключающихся в зависимостях управляющих внутренних моментов от времени. В статьях [12, 13] решается подобная задача для ограниченных случаев: одномерного и двумерного без учета сферичности земной поверхности.

• 1    Уравнения движения системы

Будем рассматривать КА ДЗЗ с двигателями-маховиками как твердотельную систему, состоящую из несущего (основного) динамически несимметричного твердого тела, внутри которого расположены три одинаковых, динамически симметричных ротора, которые могут вращаться вокруг своих осей, совпадающих с главными осями инерции всей системы [13]. Подобные КА называют гиростатами или спутниками-гиростатами. Динамические уравнения движения такой системы приведены, например, в [2, 11].

Согласно методике, приведенной в [14], введем в рассмотрение систему координат CX_aY_aZ_a с началом отсчета в центре масс Земли C , которую условно будем считать абсолютной. Ось CZ_a направим вдоль оси вращения Земли. С центром масс O спутника-гиростата свяжем две системы координат: орбитальную OXYZ , и связанную Oxyz (рис. 1).

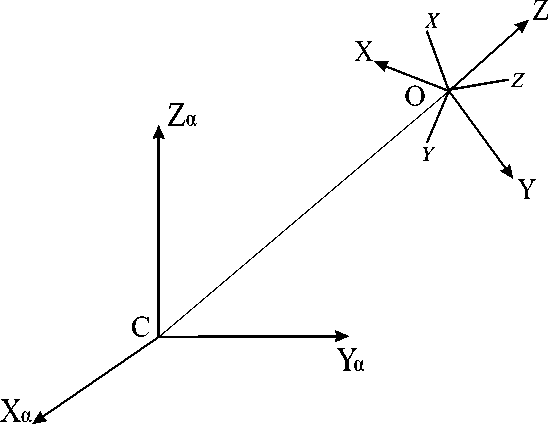
Рис. 1. Абсолютная, орбитальная и связанная системы координат

Для определения ориентации КА будем применять классические углы Эйлера ϑ , ψ , ϕ (нутации, прецессии и собственного вращения). Проекции вектора угловой скорости несущего тела p , q , r на оси связанной системы координат выражаются кинематическими соотношениями [14]:

a21 = sinψcosϕ+ cosψcosϑsinϕ, a22 =-sinψsinϕ+cosψcosϑcosϕ, a23 = -cosψsinϑ, a31 = sinϑsinϕ, a32 = sinϑcosϕ, a33 = cosϑ.

Динамические уравнения строятся с помощью теоремы об изменении момента количества движения:

Ap + ( C - B ) qr - 3 ® 2 ( C - B ) a ₃₂ a ₃₃ + 1 6 1 + 1 ( q a ₃ - r e ₂) = 0,

Bq + ( A - C ) rp - 3 ® ₀²( A - C ) a ₃₃ a ₃₁ + I d ₂ + 1 ( r a ₁ - p a ₃) = 0,     (2)

Cr + ( B - A ) pq - 3(i p . ( B - A ) a ₃₁ a ₃₂ + I d ₃ + 1 ( p a ₂ - q a ₁ ) = 0, где A , B , C — главные центральные моменты инерции системы относительно осей связанной системы координат; I — момент инерции каждого ротора относительно своих осей вращения; a ₁, a ₂, а ₃— относительные угловые скорости роторов. В связи с тем, что иное внешнее воздействие, кроме гравитационного, не учитывается, в правых частях уравнений (2) остаются нули.

Для описания движения роторов также на основании теоремы об изменении момента количества движения составляются следующие уравнения:

A 1 ^{( p + a} i ) = M a ;

B 2 ^{( q} + ^a 2 ) = M в ;                           ⁽³⁾

c3(r+a3)=My , где Ma, Mp, MY — управляющие внутренние моменты, действующие со стороны несущего тела на роторы. В работе ставится задача определения этих моментов, которые обеспечат в течение некоторого времени нацеливание КА ДЗЗ на объект наблюдения.

А^а

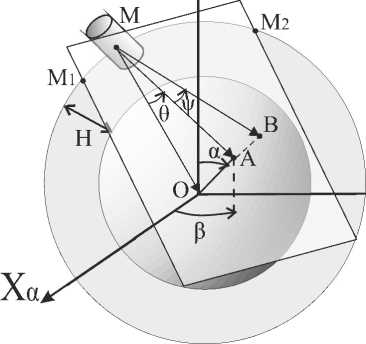
Рис. 2. Определение зоны видимости объекта и углов ориентации

>

Ya

• 3    Определение области видимости объекта

Предположим, КА движется по орбите, уравнение которой в системе координат OX a Y a Z a имеет вид:

у2 + z2 = (R + H )2, где R — радиус Земли.

Уравнение поверхности Земли в координатах OX a Y a Z a :

X2 + у2 + z2 = R2.

Касательную плоскость к поверхности Земли (5) найдем по формуле:

FX( x - x о)+Fy( у - у о)+Fz(z -z о) =0, где Fx, Fy, Fz — производные уравнения (5), (x0, у0, z0) — координаты объекта.

Решив систему уравнений (4) и (6) с условием x = 0 , получим координаты точек на орбите M 1 , M ₂ , которые появляются при пересечении касательной плоскости с орбитой и являются границами области видимости объекта.

• 4    Внутренние управляющие моменты

Построив векторы MA, MB , MO , получим зависимости углов нутации и прецессии от времени (рис. 3, 4):

& = Arccos

uuur uuuur

MA • MO

uuuur uuuur

[ I MA I-I MO\ J

у = Arccos

uuur uuur

MA • MB

uuuur uuuur

I MA -| MB J

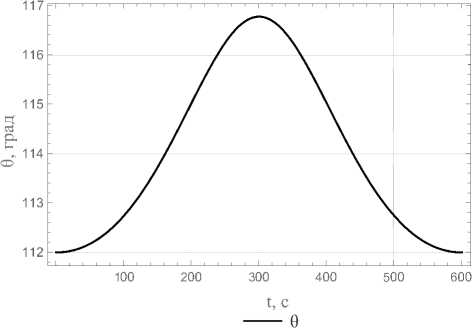
Рис. 3. Зависимость угла нутации от времени

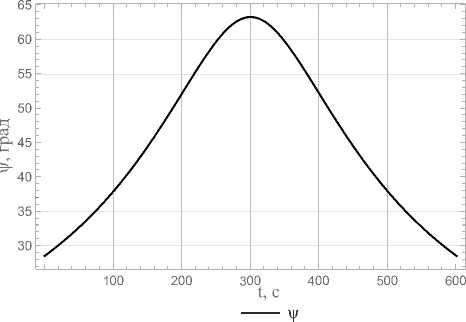
Рис. 4. Зависимость угла прецессии от времени

Чтобы определить зависимости собственных угловых скоростей вращения роторов проинтегрируем систему дифференциальных уравнений (1)-(2) численно с учётом (7)-(8) при соответствующих начальных условиях: c i (0) = 0, (j i (0) = 0, i = 1,3 ; инерционно-массовых характеристиках системы: A = 1000 кг • м 2 , B = 1500 кг • м 2 , C = 2000 кг • м 2 , I = 100 кг • м ²; параметров, характеризующих орбиту: H = 500 000 м ,

R = 6371100 м и конкретном положении объекта наблюдения: a = 3 п /7 , в = л/ 6 . Численные зависимости угловых скоростей роторов от времени приведены на графиках (рис. 5).

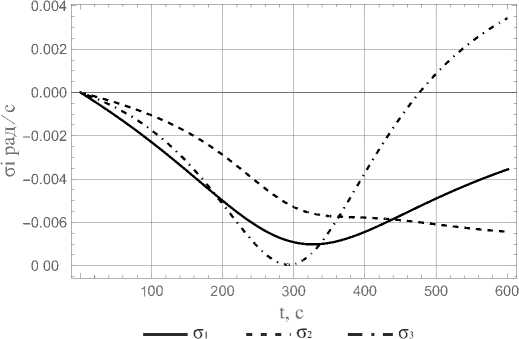
Рис. 5. Зависимости собственных угловых скоростей роторов от времени

Чтобы определить законы изменения внутренних управляющих моментов (рис. 6), подставим зависимости ускорений, полученные выше, в

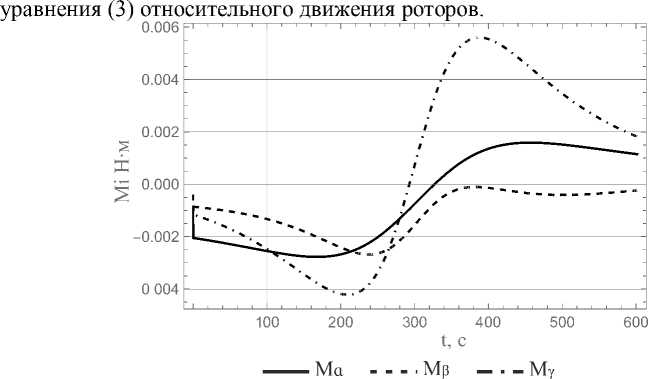
Рис. 6. Зависимости внутренних управляющих моментов от времени

Заключение

К основным результатам работы можно отнести аналитические зависимости углов нутации и прецессии от времени, при обеспечении которых ось КА ДЗЗ всегда направлена на объект наблюдения; определение области видимости объекта, ограниченной из-за сферичности Земли; численные зависимости от времени внутренних управляющих моментов, обеспечивающих необходимые углы ориентации КА. Кроме того, отдельно следует отметить, что в данной работе учтено воздействие гравитационного момента.