Влияние шума квантования на информативные параметры эхо-сигнала при условии возмущенной атмосферы

Формирования ионного портрета атмосферных осадков и влагосодержащих сред связано с охраной окружающей среды, содержанием патогенных ионов в каплях дождя, продуктах питания и рядом других актуальных научных задач. Главное препятствие в решении этих задач есть получение достоверных оценок диэлектрической проницаемости и проводимости атмосферной влаги и влаги содержащейся в биологических структурах.

Сущность этого препятствия в том, что необходимая для получения таких оценок информативная составляющая эхо-сигнала – квадрат математического ожидание модуля наведенного дипольного момента капли является малой величиной относительно мощности принимаемого эхо-сигнала, отраженного от влагосодержащей среды. При этом сама по себе мощность эхо-сигнала есть случайный вектор.

Описаны принципы формирования оценок диэлектрической проницаемости и проводимости капель дождя. Они основаны на известных выражениях для наведенного дипольного момента капли дождя, уравнении радиоэхо для объемно протяженных объектов и уравнений Дебая для пересчета (приведения) значений оценок к достоверным значениям. Изложены принципы формирования несмещенных оценок мощности радиоэхо от до- ждя. Определены условия, когда они получаются состоятельными, эффективными и несмещенными с точки зрения минимума среднеквадратической ошибки.

Данные о физических свойствах дождевых капель: K w - наведенном дипольном моменте капли, l ( f ₀ , K w , R ) - затухании при распространении сигнала вдоль сферической координаты дальности, а также данные о физических свойствах облачно-дождевых систем: R – интенсивности дождя и M – водности облачно-дождевой системы лежат в основе некоторых физико-математических моделей. Эти модели ориентированы на решение следующих группы задач: радиофизические задачи, задачи связанные с алгоритмами обработки сигналов и электрохимические задачи. Изложение статьи соответствует диаграмме изображенной на рис. 1.

Формулировка радиофизической задачи

Статистическая оценка диэлектрической проницаемости s' и проводимости атмосферной влаги 6 в условиях возмущённой атмосферы является предметом исследований данной работы. Проводимость капель дождя линейно зависит от минерализации. Для тщательно очищенной воды естественная проводимость 6 = 0,38 ■ 10 - 5 См / м,

Пер ед ат-

Первый уровень элекрохи-мической задачи (математическая модель оценки за-загрязненности воздушного бассейна). Имеет ли место загрязнение капель дождевой воды в пределах санитарной нормы? Бинарная оценка (имеет/или не имеет)

по «частному» оценочному критерию матическая модель оцен-

Ф -

Второй уровень электрохимической задачи. Мате-

Второй уровень радиофизической задачи (математическая модель квантованного сигнала) от капель дождя)

последетекторное накопление эхо-сигнала от дождевых капель ки ионного «портрета» капли дождевой воды по

Третий уровень радиофизической задачи формирование оценки матрицы комплексной диэлектрической проницаемости (проводимости и дилектрической проницаемос ти капель дождевой воды)

чик СВЧ-мощности

Приемник СВЧ-мощности

Первый уровень радиофизичес-ческой задачи (математическая модель формирования эхо-■—<             сигнала от

__________ капель дождя)

Импульс- I • ¹ / / ный объем / / / !

Рис. 1. Диаграмма деления физико-математической модели на блочно-составные части

а для дождевой воды ионная проводимость а = 5 • 10 ^{- 4} + 100 • 10 ^{- 4} См / м [1; 2].

Наведенный дипольный момент капель дождя K_w связан с их физическими характеристиками: е’ - вещественной частью комплексной диэлек

трической проницаемости и проводимостью а :

K w

= ( m2 (ю)- 1)

(m2 (щ) + 2)

где m ( щ ) = ( n ( щ ) - jk ( щ ) ) =е ( щ ) р = (V ( щ ) + i е"( щ ) ) р -комплексный относительный показатель преломления; е ( щ ) = е‘ ( щ ) + i е"( щ ) - относительная

комплексная диэлектрическая проницаемость капель дождя; р - магнитная проницаемость воды р = 0,999991 [3]; а - удельная проводимость капель дождя,

k ( щ ) =

- Р 2

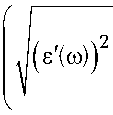
^ аХ v 2пе0 c у

^- 8 ^{( щ )}

7

– коэффициент поглощения;

/

1 С

n(щ) = 1 2 Р fE (щ)) V

12+

аХ

12пео c J

А

^+Е ' ⁽ щ )

7

– действительный показатель преломления;

е‘ - вещественная часть комплексной диэлек

трической проницаемости; s" - мнимая часть

комплексной диэлектрической проницаемости;

а - удельная проводимость среды распространения (капли воды); Х - длина волны зондирующе

го сигнала; щ - круговая частота зондирующего сигнала; c = 1/ ^^Ц о - скорость света в вакууме; 8 о - электрическая постоянная (электрическая

(диэлектрическая) проницаемость вакуума); Р о -магнитная постоянная (магнитная проницаемость вакуума).

Получив эффективные, состоятельные и несмещенные оценок величин | к w ( Х 1 )| и | к w ( Х 2 )| и используя формулы (1)-(3) решается система уравнений относительно е‘ и а . Оценки - | к w ( Х i )| есть решения уравнений эхо-сигнала дождя (метеорологические уравнения) [4]:

P) r o ) = ^а | =

= Al² ( Г о , K w , R )| K w ( ^Х i )|² X                             (4)

x N о ( a R -Р )^{- 7} y ( ^7, а R -Р D max ) .

Здесь коэффициент A - связывает все конструктивные априорно известные параметры измерительной системы

<           _3 _п2

A = —---— Г cth(aF т)- 1/ ( aF т)1—

V      2 г о Х 2 8 П2 2 ^{L    (}     )     (    ) ^J 2 J

в (4), то есть (постоянные параметры фиксированные для каждого текущего зондирования). Где l r ( а , F , т ) = Г cth ( aF т ) - 1/ ( aF t ) J - коэффициент потерь, в приемнике обусловленный ограниченной

полосой пропускания; a =

п

2ln2

- первый коэф-

фициент формирования амплитудно-частотной

характеристики; F - ширина полосы пропускания приемника по уровню половинной мощно-

сти; т - длительность зондирующего импульса; P_u – мощность, излучаемая передатчиком; g ² – коэффициент усиления датчика (антенны) одновременно на прием и передачу; ^ - значение на-

клонной дальности (сферической координаты) до центра импульсного объема; 91 - угловая ширина (в радианах) однократно используемой (либо на прием, либо на передачу) осесимметричной диаграммы направленности антенны (или датчика); l2 (/0,Kw,R) - оценки затухания при распространении по сферической наклонной дальности (трассе распространения) туда и обратно; R - оценки интенсивности дождя; Nо, а, в - априорно известные условия наблюдений облачно-дождевой системы (время суток, фаза дождя); у(-) - неполная Гамма функция [5]; Dmax - максимальный диаметр капли дождя. В основе указанной задачи лежит численное решение уравнения (4). Решение уравнений (4) должно обеспечивать получение достоверных оценок |Kw (X1 ) и |Kw (^2 ) на частотах X1 и ^2-

Принципы формирование несмещенных, состоятельных и эффективных оценок ^Kw (^X 1 )| , • ( Г о , ^K w , ^R ) и R i

При решении уравнений (4) необходимо:

• 1.    Обосновать режимы сканирования пространства и юстировки системы, при физически реа-

• лизуемых вычислительных ресурсах системы и физической реализуемости, учитывающей перемещения дождя из-за ветра. Режимы измерения должны обеспечивать наилучшую сходимость оценок диэлектрической проницаемости и проводимости капель дождя. Должно быть наилучшее сочетание следующих характеристик измерительной системы: объема выборки, разрядности аналого-цифровых преобразователей, относительной нестабильности частоты когерентного гетеродина измерительной системы, общего объема аппара-
• турных затрат, реализации алгоритмов в масштабе реального времени.

• 2.    Статистические алгоритмы обработки сигналов должны быть такими, чтобы получаемые из (4) оценки были несмещенными, состоятельны-

• ми, эффективными и с минимальной дисперсией. Смещение оценки P(/0) имеет три составляющих. Алгоритмы устранения смещения оценок |Kw (Xi) должны убрать все составляющие. Сигналы, принимаемые по боковым лепесткам в

смежных точках дальности m1 и m2. Мощность шума квантования [6], зависит от уровней сигналов, принимаемых по боковым лепесткам. Мощность теплового шума приемника. Алгоритм выделения несмещенной выборочной оценки мощности сигнала метеоэхо [6; 7] (по сканам с сигналом одной той же длины волны и длительности зондирующего импульса) есть:

z z

P !; ( ^Г 0 ⁾ = D Z^{( Г} 0 ⁾ =

= D s ( - о ) - D n ( - о ) - D z ( - о ) - ^{2 K} й( - о ) -             (5)

- ^{2 K} L n ( Г о ) = D 8 — D n - D z ( Г о ) - ^{2 K} Zn

Здесь D а ( - о ) - оценка вектора мощности метеоэхо получаемая в результате выполнения следующих алгоритмов:

• •    алгоритма выборочного среднего по n сканам: 1 ⁿ

m j = n E (sgn IV ^х ) I)V ^х ) , ) = ^s , c ^{;                 (6)}

i = 1

s , c – синфазная и квадратурная составляющие оценки; n – количество сканов антенной системы; K - коэффициент корреляции векторов Z и п

Z,n xj - выборочная амплитуда для фиксированной точки пространства на дальности ^; sgn |^xj| -определения знака выборочной амплитуды (например, с помощью амплитудно-фазового детек- тора при предположении, что система истинно когерентна);

• •    выборочного алгоритма второго начального момента (при условии, что сигнал прошел АЦП):

n ₂

D ⁸ )j ^{( г} о ⁾ = n Е ( ( ^{sgn 1} ) I) fi " m j )

i = 1 x

+

⁺ D n ( ^г о ) ⁺ D z ( ^г о ) ) ,

) = ^s ,^c;

Dn (-о) - оценка вектора мощности теплового шума приемника; D^(-о) - оценка вектора мощ- ности шума квантования, которая имеет следую- щий вид:

z

D Z^{( г} о ^{) =}

Г 9 А ² --+ 12

x

А

п

2 ю n

I EZqn2

^{1 Е} ( n ) ²

n

А2 + M y(z1Lqn2

• ¹² W ^Е ( n )²

  f 2 п

  cos nm

  X А

  
  

  f 2 п

  cos nm

  X А ¹

  
  
  
  

• 3.    Обосновать принцип вычисления из (4) оценок физических величин I ( 70, K w ( х ) , R ) ; K w ( x ) и R . Он должен учитывать, что первые две зависят от длины волны, а третья не зависит.

• 4.    Привести оценки С и S к достоверным значениям с помощью формул Дебая для пресной воды, учитывая температуру осадков и лаборатории при измерении проводимости капель дождя.

2 п ² о |

Здесь q = e ^А 2 ; А - дискрета квантования; Z - двухмерный вектор шума квантования, являющийся результатом нелинейного «пилообразного» преобразования входного двухмерного нормального вектора п = ^ + n с ненулевыми, в общем случае, математическими ожиданиями значений его координат. Характеристика преобразования

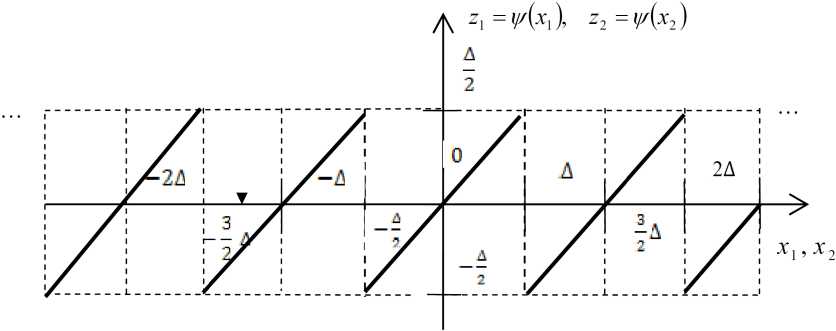
Рис. 2. Нелинейная пилообразная характеристика преобразования значений x 1 и x 2 для координат вектора n = ( П 1 , П 2 ) в шум квантования

значений каждой из координат вектора П изображена на рис. 2.

Заключение

В работе изложены основные принципы формирования следующих оценок: |Kw (Х1 )| - оценки квадрата наведенного дипольного момента капли дождя, I2 (/0,Kw,R) - оценки затухания при рас- пространении по сферической наклонной дальности (трассе распространения) туда и обратно, R -интенсивности дождя. Сформулированы условие получения достоверных оценок для оценок су и S. Кроме того сформулированы и обоснованы все необходимые и достаточные условия для получения несмещенных, состоятельных и эффективных оценок Kw (Х1 )| , /2 (/0, Kw, R) и R, а также су и s.

Работа описанного алгоритма перед ее реализацией в опытном образце должна быть представлена в виде комплексной математической модели, которую необходимо описать комплексом программ математического моделирования. Это необходимо чтобы объемы аппаратурных затрат, стоимость и предельно достижимые оценки дисперсий оцениваемых параметров были наилучшими.