Влияние шумов на погрешность измерений экспериментального лазерного кругломера

Приборы на основе оптической триангуляции достаточно широко применяются сейчас для трехмерного сканирования и технического зрения. Зачастую они входят в состав систем автоматизированного проектирования и инженерного анализа. Однако недостаточное качество входного сигнала, или, иначе говоря, отклика первичного преобразователя, в ряде задач серьезно сдерживает их распространение. При этом одним из основных факторов являются оптические и электронные шумы. В связи с чем, конечно, наряду с поисками мер по борьбе с источниками этих шумов и устранению их причин, также являются актуальными исследования алгоритмов обработки входного сигнала на стойкость к их действию. В последнем случае, наряду с фильтрацией шумов, положительный эффект дает

также статистическая обработка. При последней сигнал представляют как случайный процесс с наличием некоторой постоянной составляющей, либо тренда, которые и содержат информативные параметры. Искомые параметры, очевидно, имеют свойство быть более устойчивыми к действию шума, чем единичный отсчет, или же, например, экстремум, как это имеет место при поиске максимума отклика.

Цель нашей работы – уменьшение влияния шумов на входной сигнал типичного триангуляционного прибора. Это должно содействовать расширению области применения приборов указанного типа. В данной работе мы ограничились более подробным рассмотрением двух наиболее часто используемых алгоритмов статистической обработки.

ПРЕДПОСЫЛКИ

В нашей работе представлены результаты численных расчетов изменения величин информативных параметров двумерного лазерного триангулятора [1] под влиянием шумов. Этот перспективный прибор, предназначенный для контроля качества формы рабочих поверхностей подшипников, разрабатывался в Самарском филиале Физического института РАН. Результаты расчетов получены с помощью специально соз- данной компьютерной программы. Программа создана на MathCad 14.

Сущность способа, лежащего в основе действия исследуемого прибора, заключается в сканировании контролируемой поверхности узким сфокусированным пучком света лазера и регистрации местоположения пучка света, зеркально отражаемого при этом данной поверхностью, позиционно-чувствительным (в данном случае матричным) фотоприемником на основе прибора с зарядовой связью (ПЗС). Фотоприемники этого типа широко распространены в настоящее время. Идея способа в чем-то напоминает датчик волнового фронта Шака-Гартмана [2], только у нас гартманограмма, в виртуальном виде, получается последовательным сканированием с дискретным шагом, что заменяет множество субапертур. Это оправдано при контроле поверхностей относительно большой и сложной кривизны, которые встречаются, например, в машиностроении и которые, разумеется, не предполагается использовать в качестве элементов оптики, как это обычно имеет место в задачах с контролем гармановскими датчиками.

МЕТОДИКА ИССЛЕДОВАНИЙ

Лазерный пучок в кругломере, отраженный от контролируемой поверхности, несет нужную нам информацию. Этот пучок может быть удовлетворительно описан астигматическим, в общем случае, гауссовым пучком [3]. Функция, которая его описывает, есть двумерный гауссиан. Особенности гауссовой функции, точнее, экспоненты - этой функцией она выражена - позволяют ее представить в виде произведения двух одномерных гауссианов [4]. Это позволяет, в свою очередь, создать, при необходимости, расчетную модель погрешности, исследовав по отдельности влияние одинаковых факторов на погрешности указанных двух сомножителей – одномерных гауссианов.

Отметим, что рассмотрение одномерного гауссиана также вполне подходит для оптических полей, формируемых цилиндрическими оптическими элементами, то есть фокусирующих пучок света в линию. Для примера можно назвать похожую по идее систему автоматизированного определения дефектов формы и структуры зеркально отражающих поверхностей [5], или триангуляционные схемы с использованием метода «светового сечения» [6].

Таким образом, в качестве модельной функции нами был взят, для простоты, одномерный гауссиан:

y 0 ( n ) = exp f - ^( x ^L ) ,     (1)

V L 7

верхностью, на позиционно-чувствительном фотоприемнике, то есть входной сигнал в триангуляторе в заданный момент. Информативными параметрами в двумерном лазерном триангуляторе являлись координаты центра лазерного пучка на фотоприемнике. Параметр x ₀ был задан равным нулю, а амплитуда была принята равной единице. На наш взгляд, это не снижало общности рассмотрения, но, в то же время, упрощало формулы для моделирования.

Шумы, возникающие как от электроники, так и от лазера, моделировались, для простоты, белым шумом, имеющим аддитивную и мультипликативную составляющие:

y ^{( x} ) = V 1 - A + A X ^ y o^{( x} ) - B % . (2)

Первое слагаемое моделировало мультипликативную составляющую шума (неоднородность чувствительности элементов ПЗС-фотоприемника), второе - аддитивную (погрешность амплитудно-цифрового преобразования); c и x- случайные величины с равномерных распределением в интервале значений больше нуля, но меньше единицы; c и x не зависели друг от друга.

Величины коэффициентов A и В , задающих в модели амплитуду шума, были выбраны нами из данных наших же экспериментов [7], а также сведений из литературы [8]: A =0,04, В =0,005.

В нашей программе присутствовали два алгоритма расчета центра пятна. По первому из них этот центр вычислялся как «центр тяжести», или, как говорят оптики, «энергетический центр». Он определялся как первый начальный момент модельной функции. Для статистической оценки искомой величины в программе задавалось количество повторений процедуры этого алгоритма. По выборочной дисперсии рассчитывалась статистическая оценка (в виде С.К.О.). Другие параметры сигнала и шума пользователь должен был задавать самостоятельно.

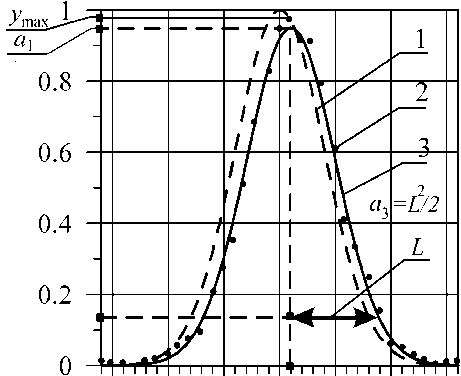
По второму алгоритму искомый центр определялся как координата максимума аппроксимирующей функции. Аппроксимирующая функция в программе задана такого же вида, как и модельная. Это гауссиан с тремя искомыми параметрами (см. рис. 1):

y ( x ) = a exp[( x - a ₂) ² 1 a ₃] . (3)

где a ₁ – амплитуда; a ₂ – координата максимума (нужная нам величина); a ₃ – параметр ширины, a ₃= L ² / 2. Аппроксимация проводилась по известному методу наименьших квадратов. Для этого находили a ₁, a ₂, a ₃ из системы уравнений:

F 1 ⁽ a l , a 2 , a 3 ) =

= E y ^{( x )=}i y - a l ^ex P

-

^x (4)

a ₃

где x задавался дискретными отсчетами.

Он моделировал распределение мощности лазерного пучка, отраженного контролируемой по-

= exp

-

a ₂

a ₃

= 0 ;

Интенсивность у. отн. ед.

F 20 +

F 3 0 ⁺

6F dF2 0

—— 8 1

8 a₁

8F ^dF3 0

-— 8 1 d a ₁

! ^d F 2 0

d a ₂

! ^d F 30

⁸ 2 d a 2

, d F 20 d a₃

, 8 F 30 d a ₃

8 3 = 0 ; (11)

8 3 = 0 , (12)

а2

-15 -10 -5   0    5   10 15

Координата х, пиксели

Рис. 1. Аппроксимация гауссианом:

1 – функция без шума; 2 – отсчеты функции с добавлением шума; 3 – аппроксимирующий гауссиан

F 2 (a₁, a 2 , a 3 ) =

=e

i

У ⁽ x М у ,

^^^^^

^a1 exp

^^^^^

^^^^^

a ₂ ) 2

> X

^X exp

a ₃

a ₃

x, = 0 ;

F 3^{( a} ₁, a ₂, a 3 ) =

= E y ^{( x} M у , - a exp

-

X

i

a ₃

^^^^^

^X exp

a ₃

x² = 0 .

Для решения (4 - 6) использовался метод Ньютона. При этом первое приближение выбиралось в виде:

^a i0 = m ^ax( у i ) ;

E y x a 2 0 = V"1     ;

E у i

i

a 3 0 =

^^^^^

² E У ⁽ x - a 2 0⁾² E y

.

После решения системы уравнений

QF F + —^ F 1 0 ⁺ д oa₁

, ^d F 10     , ^d F 10

⁸ 1 +       8 2 +       8 3 = 0 ^; (1⁰⁾

о a ₂        о a ₃

где F _{1 0}= F ₁( a _{1 0}, a _{2 0}, a _{3 0}); F _{2 0}= F ₂( a _{1 0}, a _{2 0}, a _{3 0}); F 3 ₀= F 3 ( a 1 ₀, a 2 ₀, a _{3 0}), определялась поправка 81 , s ₂, 83 . Затем делалась замена: a 1 ₀ ^ a 1 ₀+ 81 ; a _{2 0} ^ a _{2 0}+ 82 ; a _{3 0} ^ a _{3 0}+ 83 ^в (10 -12) и находились следующие поправки 81 , 82 , 83 , продолжая процесс до тех пор, пока не выполнялись условия: | 81 |< 81 min ; | 8 ₂|< ⁸ 2 min ; | ⁸ 3 |< ⁸ 3 min ^.

Пределы допустимых в наших расчетах погрешностей определения параметров гауссиана (амплитуды, координаты центра и полуширины) были заданы соответственно 0,003 (от максимума гауссиана), 1´10^-6 (доли дискретного отсчета ПЗС-фотоприемника) и 0,01 от L (1).

Из-за значительно большего времени счета, по сравнению с первым алгоритмом, статистическая оценка по второму алгоритму в программе не проводилась. Для этого мы использовали другую программу статистических расчетов, специально созданную нами. Файл данных для нее мы формировали с клавиатуры.

Существенным моментом в нашей программе было применение цифровой адаптивной пороговой фильтрации сигнала, при которой отчеты, меньшие некоторого порогового уровня, заданного в долях максимума отклика, отбрасывались, чтобы они не увеличивали погрешность определения центра отклика. При этом заданный уровень также должен был быть не менее уровня фонового шума. Этот фактор, связанный с отчетами распределения мощности лазерного пучка на краях одномодального оптоэлектронного отклика (1), был обнаружен нами из численного моделирования, благодаря чему мы заблаговременно внесли в нашу программу соответствующие изменения. При этом уровень порога фильтрации был нами выбран опытным путем (по критерию минимума погрешности определения координаты максимума) равным exp(-2) от максимума оптоэлектронного отклика (это 13%).

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Для верификации нашей программы, мы сравнили наши результаты с полученными ранее [9] другими специалистами, которые исследовали влияние дискретности на погрешность оптического триангулятора. В их работах центр отклика определялся по «центру тяжести». Для сравнения мы задали нулевой уровень шума. Сравнение показало, что результаты удовлетворительно совпадали, что придало нам уверенности в правильности наших вычислений.

По результатам работы программы построены гистограммы, по которым видно отклонение рассчитанной координаты центра (или же максимума), возникающее при действии шума. Гистограммы статистической выборки в обоих случаях (объем выборки мы брали равный 10000) практически соответствовали нормальному распределению непрерывной случайной величины.

Результаты показали, что алгоритм аппроксимации гауссианом имел в полтора раза большую погрешность от влияния шумов, чем алгоритм «центра тяжести» (см. рис. 2). Очевидно, что учет двумерности оптического отклика не мог бы качественно изменить этот результат.

Следует признать, что при сравнении с алгоритмом (который мы здесь не рассматривали) поиска центра по медиане, то есть, по равенству площадей под графиком функции отклика, эффект был бы еще скромнее, хотя и не слишком значительным. Утверждают, что это свойство медианного алгоритма отметил еще выдающийся российский ученый Д. И. Менделеев.

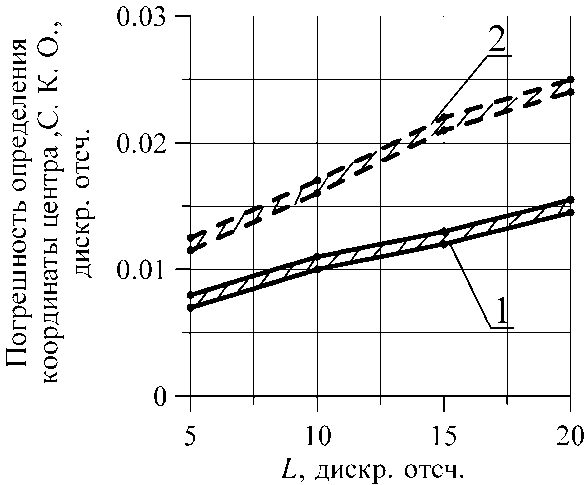
Рис. 2. Результаты численного моделирования:

1 – алгоритм «центра тяжести»;

2 – аппроксимация гауссианом

Выражаем признательность В. Н. Подвигину за полезные обсуждения и помощь в работе.