ВЛИЯНИЕ СПЕКЛ-ПОЛЕЙ НА РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ ПРИ КОНТРОЛЕ ДЕФОРМИРОВАННОЙ ПОВЕРХНОСТИ НИЗКОКОГЕРЕНТНОЙ ИНТЕРФЕРЕНЦИОННОЙ УСТАНОВКОЙ

В современном метрологическом обеспечении измерения формы поверхности являются одной из важнейших задач [1, 2]. Для исследования поверхности существуют механические и оптические методы и технические средства, которые способны контролировать рельеф поверхности с точностью до десятых долей микрометра [3]. Исследователи отмечают, что на практике при измерениях механическими приборами и комплексами шероховатости поверхности не всегда можно добиться высокой производительности. У данных технических средств в течение короткого времени изнашивается контактный элемент, а также увеличивается погрешность измерений при контроле рельефа поверхности с малой устойчивостью [4]. В настоящей работе речь пойдет о современном оптическом методе измерения неровных поверхностей и влиянии спекл-полей на результаты измерений.

Касаемо оптических методов и средств контроля рельефа поверхности, то они могут быть представлены приборами и комплексами, где оптические системы построены на разных оптикофизических явлениях. Например, на анализе расходимости излучения, отраженного от поверхности, на исследовании фокусировки отраженного излучения, на изменении показателя преломления среды между экспозициями, с компенсацией поперечного сдвига изображений, с применением несущей частоты спекл-полей пространственно когерентного излучения, а также при исследовании излучения с ограниченной временнóй когерентностью и т.д. [5–7].

В научно-технической литературе многие авторы отмечают тот факт, что цифровые автоматизированные интерференционные приборы и комплексы, работающие в низкокогерентном свете, для изучения поверхности сложной формы перспективны и актуальны. Их преимущества над оптическими приборами и комплексами геометрической оптики заключаются в следующем: чувствительность, диапазон измерений, расстояние до измеряемой поверхности не зависят от апертурных углов наблюдения и освещения [8]. Интерферометры, построенные по классическим схемам, не пригодны для измерения негладких поверхностей, т.к. используют высококогерентные источники света (лазеры), где длина когерентности источников варьируется от 10 мм до 50 мм. А это означает, что при анализе светового излучения, отраженного от исследуемой поверхности сложной формы, данные о рельефе возможно получить только в пределах длины когерентности, поэтому, кроме шума, никакой информации извлечь не получится [9].

В современных автоматизированных интерференционных приборах, работающих в низкокогерентном свете (АИПНК), используют источники белого света — суперлюминесцентные диоды, у которых длина когерентности находится в диапазоне от 100 до 1 мкм. Длина когерентности источника излучения является ключевым параметром этих приборов, т.к. чем меньше длина когерентности, тем выше точность измерения микрорельефа поверхности [10–14].

АИПНК достигли больших успехов в практическом применении за счет компактности, простоты эксплуатации и динамики измерений [9, 15–20]. Появилась информация анализа метрологии негладких поверхностей в разных режимах измерений (триггерный, сканирующий). Решены вопросы построения и эксплуатационных характеристик АИПНК. Разработчики постоянно совершенствуют функциональные возможности и повышают информационное содержание измерений этих приборов.

Поэтому представляет интерес влияние спекл-полей на амплитуду выходного сигнала при функционировании низкокогерентной интерференционной установки.

Целью работы явилось получение выражения для оценки амплитуды выходного сигнала при изменении параметров оптической схемы экспериментальной установки.

ПОСТАНОВКА ЗАДАЧИ

Рассмотреть основные свойства спекл-полей, которые являются ключевыми при контроле деформированной поверхности низкогерентной интерференционной установкой. Методом контроля негладкой поверхности с использованием низкокогерентного излучения выявить влияние спекл-полей на результаты измерений. Получить аналитическое выражение для амплитуды выходного сигнала при функционировании установки.

СВОЙСТВА СПЕКЛ-ПОЛЕЙ

Спекл-поля возможно наблюдать при освещении шероховатой поверхности как лазерным, так и частично когерентным излучением в пределах длины когерентности при отражении светового потока. На рис. 1 показана схема формирования спекл-полей при контроле деформированной поверхности. На экране N образуются темные и светлые области — это результат сложения элементарных световых волн.

Известно, что распределение интенсивности светового потока может быть описано выражением:

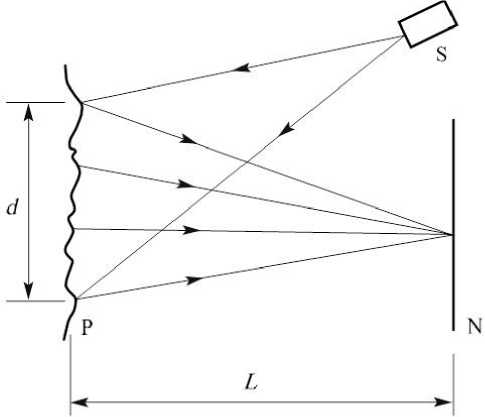
Рис. 1. Схема формирования спекл-полей при контроле деформированной поверхности.

S — суперлюминесцентный светодиод; P — деформированная поверхность; N — плоскость наблюдения

P(1) = (11cp )exp (-I!1cp ), где p(I) — плотность вероятности, I — интенсивность светового потока, Iср — средняя интенсивность.

При взаимодействии светового излучения с контролируемой поверхностью суперлюминис-центного или белого источника света спеклы можно называть суперлюминисцентными или белого света. Из приведенного рисунка видно, что сформирована объектная картина спеклов, которая создана на определенном расстоянии от деформированной поверхности. Функция автокорреляции при объектной картине может быть представлена следующим выражением:

Rr (x, y) = Ic2p [ I + sinc2 (dx/ AL )• sinc2 (d y/AL )], где RI (x, y) — функция автокорреляции в плоскости xy, λ — длина волны излучения, L — расстояние от поверхности до плоскости наблюдения.

Значение этой функции — это расстояние между точками с максимальными и минимальными интенсивностями. Это расстояние принято принимать за характерный размер элемента спекл-поля, который равен:

BS = 1.22 λL/d, где BS — характерный размер, d — диаметр пятна на поверхности.

ИНТЕРФЕРЕНЦИОННЫЙ МЕТОД КОНТРОЛЯ С ПРИМЕНЕНИЕМ ЧАСТИЧНО КОГЕРЕНТНОГО ИЗЛУЧЕНИЯ

В работе рассматривается интерференционное устройство, основанное на явлении двухлучевой интерференции, где в качестве источника излучения был суперлюминесцентный светодиод с длиной волны λ = 387 нм, длиной когерентности l c = = 6.8 мкм, мощностью излучения 1 мВт. Схема реализации экспериментальной измерительной установки показана на рис. 2.

В данном исполнении световой луч от источника света S фокусируется на зеркальную поверхность R пластинки в опорном канале и на исследуемую поверхность P объекта в объектном канале измерительной установки. Начальное состояние определяется равенством расстояний QN и QM. При таком условии интерференционное поле имеет максимум контраста.

При измерении микрорельефа поверхности зондируемая точка поверхности смешается относительно плоскости, где z = 0, на величину A z . Это смещение обусловлено движением поверхности в продольных либо поперечных направлениях относительно светового пятна на поверхности. Начальное положение точки можно вернуть перемещением зеркальной поверхности R пластинки в опорном канале на величину A z = A z .

В фотоприемном блоке D, будет наблюдаться суперпозиция световых волн, пришедших из объектного и опорного каналов. Если принять движение зеркальной поверхности в опорном канале с постоянной линейной скоростью v , то это приведет к модуляции во времени разности фаз ϕ световых волн. Тогда получим:

ϕ = 2vt · 2π / λ, где 2 — длина световой волны, 2 vt = 2Az — изменение расстояния при движении зеркальной поверхности на Az.

Изменение интенсивности определяется выражением:

I (t) = Ip + Ir + 2 fijr Ypr (t)| cos ^4nvt^, где Ip — интенсивность в объектном канале, Ir — интенсивность в опорном канале, γpr (t) — степень когерентности.

На рис. 3 приведен выходной сигнал, и видно, что максимум значения находится в точке t _m при A z = A z , 1 ₀ — точка начала отсчета. Смещения зеркальной поверхности в опорном канале характеризуются величиной A z i = fx, y ), чем определяются интервалы [ t 0 , t m ]. Индекс i определяет точку в плоскости x, y .

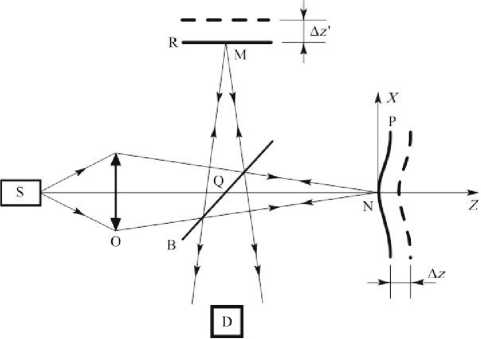
Рис. 2. Оптическая схема экспериментальной установки.

S — суперлюминесцентный светодиод; О — микрообъектив; В — светоделитель; R — зеркальная поверхность; Р — поверхность объекта; D – фотопри-емный блок

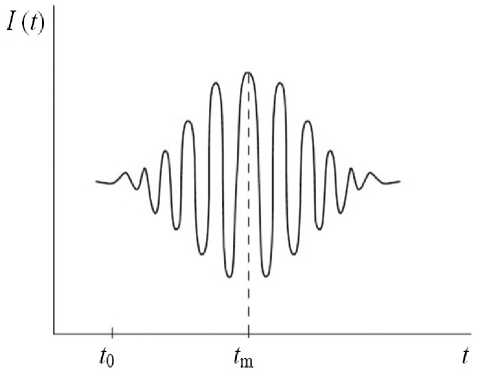
Рис. 3. Интерференционный сигнал.

В процессе эксперимента была проанализирована амплитуда выходного сигнала, т.к. она является значимым параметром для эксплуатации разработанной низкокогерентной интерференционной установки.

Этот сигнал можно представить следующим выражением:

u (t) = kJ] (IpIr ГIYpr (t)| cos f2n 2vt^ d a, n v A J где u (t) — выходной сигнал, П — апертура фотоприемника, k — коэффициент преобразования излучения в электрический сигнал, dω — элемент апертуры.

При анализе апертуры целесообразно исследовать огибающую сигнала. Тогда cos(2 π/λ · 2 vt ) = 1, огибающая U ( t ) будет равна:

^U ( t ) = k Ш I p I r T Y pr ( t ) ^d a ..

n

Интерференционное поле будет представлять спекл-поле с удвоенным характерным размером элемента спекл-поля:

B S = 2.44 λL/d .

В случае ограниченной области освещения I p ( x, y ) получим набор отдельных спеклов. Поэтому для расчета усредненной величины огибающей выходного сигнала операцию интегрирования заменим суммированием средних интенсивностей отдельных спеклов.

Рассмотрим объектный канал измерительной установки, представленный на рис. 4. Размер пятна на поверхности для суперлюминисцентного излучения можно представить в виде:

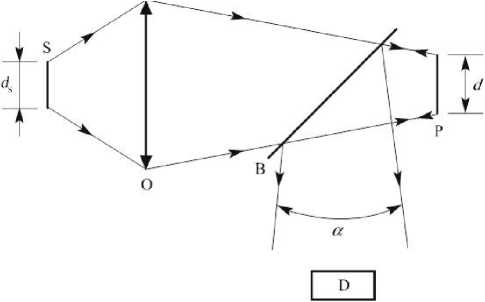
Рис. 4. Объектный канал измерительной системы.

S — суперлюминесцентный светодиод; О — микрообъектив; В — светоделитель; Р — поверхность объекта; D — фотоприемный блок

где L o — расстояние от объектива до поверхности объекта, D o — диаметр объектива.

Функция g ( x,y ) дает информацию для практически интересного случая l _c > 4λ, когда величина (λ/2π · l c ) g ( x,y ) составляет 2% от максимального значения f ( x,y ). Поэтому выражение для диаметра d пятна на поверхности Р можно записать:

d = ed +1-22—, s       Do где dS — размер выходного зрачка источника света, β — масштаб изображения.

Тогда для характерного размера элемента спекл-поля:

Ip( x, y ) = Is (x', y')®

λ f (x, y) + TV g (x, y) 2πl

Bs = 2-44----^Цт - eds +1-22 ^-^

s        _{D o}

где I p( x , y ) — интенсивность на поверхности объекта, I s ( x ', y ') — интенсивность в плоскости источника излучения, λ ср — средняя длина волны, l c — длина когерентности, ⊗ — операция свертки, f ( x,y ) — функция для монохроматического излучения, g ( x,y ) — функция для частично когерентного света.

Функция f ( x,y ) дает информацию о каждой точке в плоскости изображения, которая увеличивается в диаметре на величину:

Общее количество спеклов N S в апертуре α фо-топремного блока равно:

n = -a s     Bs2

.

Если амплитуды колебаний спеклов равны, тогда фазы равномерно распределены в промежутке от – π до π, и общая амплитуда выходного сигнала U равна:

и = Nuu ( t ).

A = 1.22 ^L o- D o

Если (1) и (2) подставить в (3), то получим следующее выражение для усредненной по ансамблю реализаций огибающей выходного сигнала { U(t) ) :

61----------Y-г (t )|. 2 eds +1-22 — s       Do

Перепишем выражение (4) с учетом (1) и (2) в следующем виде:

U ^U ( t )b

0.61 kπL ² α ²    I _p I _r

2 N s

I Y pr ⁽ t )| -

Полученное выражение позволяет оценить амплитуду выходного сигнала в зависимости от количества отдельных спеклов в апертуре фотоприемника. Формула (4) дает возможность оценивать амплитуду выходного сигнала при функционировании и изменении параметров оптической схемы измерительной установки.

ЗАКЛЮЧЕНИЕ

С первых шагов и по настоящее время в интерферометрии, где используются высококогерентные источники света (лазеры) в научных и технических исследованиях достигнуты большие успехи в измерении зеркальных, высокополированных и оптических поверхностей линзовой оптики. В настоящей работе получены экспериментальные данные о параметре, который напрямую влияет на точность измерений низкокогерентной интерференционной установки при контроле шероховатой поверхности. Получены выражения для амплитуды интерференционного сигнала, которые позволяют оценить функционирование и изменение параметров, вносимое в оптическую схему измерительной установки.