Влияние спектральной модели излучения на расчетные характеристики сложного теплообмена в пламенных печах нефтехимической промышленности

Бюллетень науки и практики / Bulletin of Science and Practice

В тепловом балансе радиантных камер трубчатых печей определяющая роль принадлежит лучистому теплообмену, доля которого может быть на порядок больше по сравнению с другими механизмами теплопередачи. Точность расчета лучистого теплообмена в значительной мере определяется корректностью модели спектра излучения компонентов, заполняющих камеру сгорания. К ним относятся, в первую очередь, пары воды Н 2 O и двуокись углерода CO 2 , а также частицы сажи, образующиеся в результате неполного сгорания топлива. Излучение паров воды и двуокиси углерода происходит в определенных интервалах спектра, излучение частиц сажи и стенок камеры характеризуется сплошным спектром. Одним из наиболее удобных методов учета селективности излучения является модель широкой полосы, параметры которой приведены, например, в работе [1].

В данной работе излагаются результаты сравнительного анализа применимости спектральных моделей широкой полосы и «серой» модели Хоттеля для теплового расчета радиантных камер трубчатых печей. За исходную принимается ступенчатая модель, учитывающая полосы 15; 4,3; 2,7 мкм излучения двуокиси углерода и 10; 6,3; 2,7; 1,5 мкм излучения водяного пара.

Лучистый теплообмен описывается системой двухмерных дифференциальных уравнений P 1 -приближения метода сферических гармоник:

д /   дрЛ\ д /   дрЛ\

Их \^¹ ~дх~) ⁺ дУ [^ ~д^ ) - ^a^^iP^

^Л 2

= ^- 4п I    ^а _Л1 ^I _Л b^(T , ^Лi^)dЛi ;

Л 1

ЯЛ = -^(Лг                              (2)

Условия однозначности на ограничивающих поверхностях с учетом диффузного отражения и излучения имеет вид:

Рл,          1              Л22

dr = 2D;a+7)\  1 ытлж -(1 -г)р^)

Здесь Ц_л. — вектор плотности потока излучения в i-той спектральной полосе; D^ , а_л.— коэффициенты диффузии излучения и поглощения в i-той спектральной полосе; 1_ЛЬ — функция Планка; г,г — степень черноты и отражательная способность поверхности.

Распределение температуры в расчетной области определяется путем решения уравнения энергии:

дТ дТ д         дТ д         дТ          Ns

Pcpu^~ + Pcpv   =-^-^Л + Лт)—\ +— \(Х + Хт)   \ + Q — div/ Цл р дх у ду дх         дх ду         ду!          Z-i 1

i=i

В качестве краевых условий на поверхности нагрева и входном сечении задается температура, на выходном сечении используется свойство «односторонних» координат [2]. Температура футеровки определяется из уравнения теплового баланса, составленного с учетом тепловых потерь через нее:

Л

~d ^(TW - Tq) = Ц к + ^ Я Л .

i=i

Конвективный поток тепла к стенке ц_к вычисляется по методу пристеночных функций [3]. В уравнениях (4) и (5) p,c_v,u,v — плотность, изобарная теплоемкость и составляющие вектора скорости продуктов сгорания; Л, Л_т — коэффициенты молекулярной и турбулентной диффузии тепла; Q — объемная плотность тепловыделения в результате горения топлива; N_s — количество излучающих полос в спектральной модели; Л ф , d — коэффициент теплопроводности и толщина футеровки, T_w, T₀ — температура внутренней и внешней поверхности футеровки.

Конечно–разностная аппроксимация уравнений (1)–(3) производится методом конечных элементов, а уравнения (4) методом интегрирования по контрольному объему [2].

Полученная в результате система алгебраических уравнений относительно узловых значений искомых величин решается методом трехдиагонального матричного алгоритма (ТДМА). Проведенные расчеты показывают, что используемая в данной работе явная схема совместного интегрирования системы уравнений (1)–(5) при тепловых нагрузках, характерных для высокотемпературных камер сгорания, является неустойчивой. Для подавления этой неустойчивости к дивергенции лучистых потоков тепла применяется нижняя релаксация с параметром о = 0,2.

Анализ проводился на примере прямоугольной радиантной камеры трубчатой печи конверсии углеводородов БПК-15. Топливо (природный газ) подается в камеру через горелки, расположенные на своде в одном ряду симметрично относительно поверхности нагрева, продукты сгорания отводятся через тоннель, расположенный на поду камеры. Наличие осевой симметрии позволяет рассматривать только одну половину радиантной камеры. Полагалось, что поверхности футеровки и нагрева диффузно излучающие и отражающие со степенями черноты 0,6 и 0,87 соответственно. Для получения замкнутой системы уравнений в расчетах входное и выходное сечения заменяются полностью отражающими поверхностями. Поля скоростей и коэффициентов турбулентного обмена определяются из решения уравнений газовой динамики и (k-ε) — модели турбулентности [4].

В модели спектра интервалы, где происходит перекрывание полос излучения водяного пара и двуокиси углерода, выделялись как отдельные полосы с суммарным коэффициентом поглощения:

^а Х ^aw^PW + ^а С^РС , (6)

где a_W, а_С — коэффициенты поглощения водяного пара и двуокиси углерода в данном интервале спектра, соответственно, P_W, Р_С — парциальные давления каждой из компонент. Учитывалось перекрывание спектральных полос 2,7 мкм; 10 и 15 мкм.

Спектральный коэффициент поглощения частиц сажи вычислялся по формуле [5]:

3пФ(Л) f

a^s= 2Х  fv где функция Ф(Л), описывающая дисперсию оптических констант сажи, по данным работы [6] в интервале спектра до 10 мкм может быть описана зависимостью:

1,75

"-

Так называемая объемная фракция сажи определялась по эмпирической формуле [7]:

fv = 0,068(2 -ат)Ср. Нр

Здесь а_т — коэффициент избытка воздуха; С р /Н р — относительный вес углерода в топливном газе.

Для вычисления интегральной степени черноты топочной среды использовалась модель Хоттеля набором четырех серых газов [6]:

^£ = ^а_п(Т){1- ^ех Р\-(а_пР ^ + a s )i эф ]}

П=0

где 1эф — эффективная толщина топочной среды, РХ(атм.) — суммарное давление водяного пара и двуокиси углерода, интегральный коэффициент поглощения частиц сажи определяется по зависимости [6]:

a_s = 0,03(0,016Т - 0,5)(2 -а_т) ^{С р}. ^Нр

На Рисунках 1–2 приведены расчетное распределение плотности интегральных по спектру лучистых потоков тепла к поверхности нагрева по длине труб и профиль температуры на оси потока по высоте радиантной камеры, определенные с использованием спектральных моделей широкой полосы и Хоттеля. Наибольшее отличие в распределениях лучистых потоков, рассчитанных по модели Хоттеля и полосовой модели без учета влияния сажи, имеет место на начальном участке течения, что можно объяснить существенной неизотермичностью потока, а также наличием «окон» прозрачности в полосовой модели. Ниже по течению, где поперечный градиент температуры становится незначительным, расчет по модели Хоттеля хорошо согласуется с результатами расчета по полосовой модели. Учет излучения частиц сажи приводит к увеличению лучистых потоков тепла и соответственно уменьшению максимальной температуры газов в топке и ее поперечного градиента. В этом случае распределение лучистых потоков, определенное по модели Хоттеля, удовлетворительно согласуется с результатами расчетов, сделанными по модели широкой полосы с учетом трех «окон» прозрачности, в которых лучистая теплопередача происходит в основном за счет излучения частиц сажи.

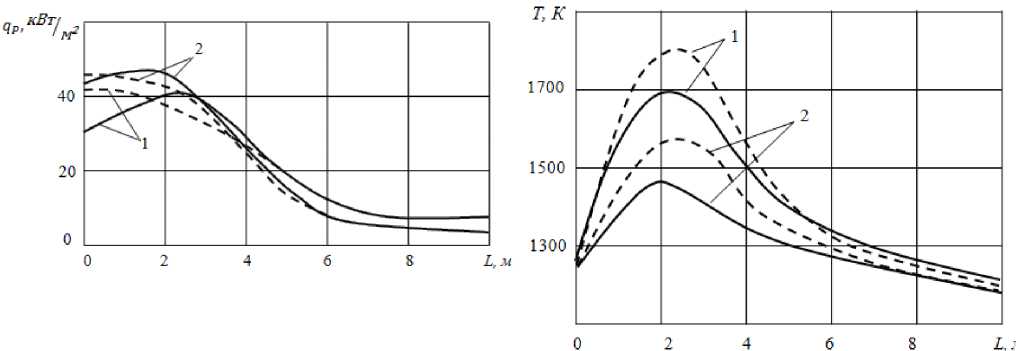
1 — расчет без учета, 2 — с учетом излучения сажи, сплошная линия — модель широкой полосы, пунктиром — серая модель Хоттеля.

Рисунок 1. Распределение плотности лучистых потоков тепла к поверхности нагрева по длине труб.

Рисунок 2. Профиль температуры продуктов сгорания по высоте радиальной камеры .

Наибольшее влияние спектральная модель излучения оказывает на профиль температуры дымовых газов в объеме радиантной камеры. В то же время это влияние на температуру газов, покидающих топку, незначительно. Наличие частиц сажи в составе продуктов сгорания снижает температуру газов на выходе из топки на 16%.

Учет излучения сажи приводит к уменьшению расчетных значений конвективных потоков тепла (Рисунок 3). Сплошной спектр излучения интенсифицирует теплообмен между стенкой и средой, вследствие чего градиент температуры вблизи стенки уменьшается. Расчеты также показывают, что в месте присоединения рециркуляционного и основного течений коэффициент конвективной теплоотдачи <т _к имеет минимум. Ниже по течению вблизи выходного сечения П К увеличивается, что вызвано сужением основного потока и его ускорением.

Бюллетень науки и практики / Bulletin of Science and Practice Т. 6. №6. 2020

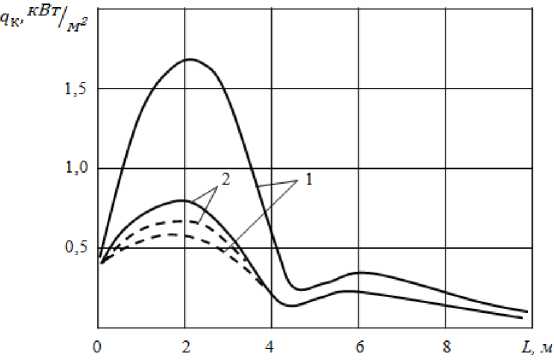
1 — расчет без учета, 2 — с учетом излучения сажи, сплошная линия — модель широкой полосы, пунктиром — серая модель Хоттеля .

Рисунок 3. Распределение плотности конвективных потоков тепла к поверхности нагрева по длине труб.

Анализ суммарной теплопередачи показывает, что интегральное тепловосприятие поверхностью нагрева, рассчитанное по модели Хоттеля, на 13% выше по сравнению с рассчитанным по модели широкой полосы. Этому соответствует снижение температуры дымовых газов на выходе из топки, что качественно согласуется и с данными других авторов [7]. Вместе с тем следует заметить, что спектральная модель излучения топочной среды слабо влияет на расчетные характеристики суммарной теплопередачи в радиантной камере рассмотренной трубчатой печи.