Влияние способа размещения компенсационных каналов на качество подавления активных шумовых помех автокомпенсатором в радиолокаторе с антенной решеткой

сигналов, антенная решетка, автокомпенсатор активных

Современные радиолокационные системы (РЛС) ориентированы на использование активных фазированных антенных решеток (АФАР). Это связано с широкими возможностями по применению алгоритмов адаптивной пространственной обработки сигналов в таких системах [1; 4]. В частности, можно организовать программный обзор пространства за счет электронного управления лучом диаграммы направленности (ДН) АФАР [1]. При этом возможно одновременное формирование нескольких лучей в различных направлениях по азимуту и углу места.

Одной из ключевых задач при проектировании РЛС с АФАР является компенсация активных шумовых помех (АШП). Оптимальное по критерию максимизации отношения сигнал–помеха решение дает применение винеровского фильтра [2]. Однако его практическая реализация в случае АФАР с большим числом элементов существенно затруднена вследствие необходимости обращения корреляционной матрицы помехи большого размера. Так, например, при использовании решетки, содержащей 64 х 64 = 4096 элементов, требуется обращение комплексной матрицы размером 4096 х 4096. Доступная в настоящее время элементная база цифровых аппаратных средств не позволяет выполнить эту операцию в реальном масштабе времени. Известной альтернативой оптимального винеровского фильтра, требующей существенно меньших вычислительных ресурсов, является автокомпенсатор АШП [2; 3]. Максимальное число помех, которые могут быть эффективно подавлены в случае использования автокомпенсатора, определяется числом компенсационных каналов.

Эффективность компенсации АШП зависит от способа размещения приемных компенсационных каналов (КК) на полотне АФАР. В статье рассматриваются различные способы размещения КК. Производится сравнительный анализ качества компенсации АШП для предложенных вариантов.

На рис. 1 изображена плоская прямоугольная антенная решетка, элементы которой расположены эквидистантно по строкам и столбцам в плоскости XOY .

Число элементов в строке решетки обозначим N_x , число элементов в столбце – N_y . Расстояние между столбцами равно d_x , расстояние между строками – d_y . Общее число элементов решетки равно произведению N_xN_y . S – вектор Умова – Пойтинга, n — нормаль к плоскости решетки. Угол прихода волны в пространстве проецируется на два взаимно ортогональных угла – азимут в и угол места б .

Будем полагать, что сдвиг фазы сигнала в приемном канале элемента, находящегося в начале координат, равен нулю. Тогда в случае плоского волнового фронта сдвиги фаз сигналов всех элементов можно записать следующим образом [2]:

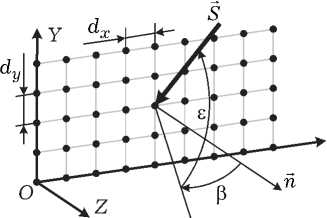
Рис. 1. Плоская антенная решетка прямоугольной формы

Ду ( i , k ) = — Г ( i - 1 ) d x si^ + ( k - 1 ) d y sin s! ,   (1)

X0

Пространственная обработка сигналов заключается в весовом суммировании отсчетов сигналов, принимаемых в элементах решетки:

y ( n ) = W ^T ■ X ( n ) , (2) где X ( n ) — вектор принимаемого сигнала, а W – вектор коэффициентов.

Рассмотрим два метода пространственной обработки сигналов в АФАР. Первый метод заключается в вычислении адаптивных весовых коэффициентов для приемных каналов всех элементов решетки. Оптимальными с точки зрения критерия отношения сигнал–помеха весовыми коэффициентами являются коэффициенты, соответствующие винеровскому фильтру, которые рассчитываются по формуле

W опт = M 1 F , (3)

где W_опт — вектор оптимальных весовых коэффициентов; M — корреляционная матрица помех; [ ] — операция комплексного сопряжения; F — сигнальный вектор-столбец, который можно записать следующим образом:

_F _ Г_е j М¹,¹) JМ¹,²)   _e ^j 41’ N y )

ee ... e

... ej Ду (2,1) ... ej ^Д У ( N x , N y )f

T где [ ] — операция транспонирования.

Поскольку КМ помех M априори неизвестна, производится ее оценка:

L

^M = L Ё X ( n ) X H ( n ) , n = 1

где L — количество временных выборок; [ ] ^H — операция эрмитового сопряжения. Оценка в виде (5) является оптимальной по критерию максимального правдоподобия [2].

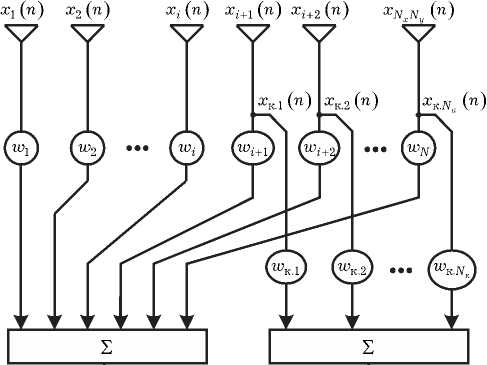
Использование автокомпенсатора АШП подразумевает формирование N _к компенсационных

У осн С71)

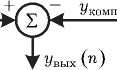
Рис. 2. Структурная схема автокомпенсатора АШП

Рис. 3. Расположение КК на полотне АФАР: а ) равномерное расположение КК; б ) расположение КК по периметру АФАР; в ) расположение КК с увеличением шага; г ) крестообразное расположение КК; д ) квазислучайное расположение КК

Выходной сигнал автокомпенсатора увых (n) , используя введенные обозначения, можно пред- ставить в следующем виде:

y вых ⁽ n ) ^у осн ⁽ n ) y комп ⁽ n ) = F H X ( n ) - W k X k ( n ) .

Работа системы пространственной обработ- ки сигналов исследовалась методом математического моделирования для АФАР размера Nx = Ny = 30 элементов. Число компенсационных каналов Nк полагалось равным 16. Рассматривались несколько вариантов расположения КК на полотне АФАР. Все эти варианты представлены на рис. 3, на котором жирными точками обозначены КК.

При квазислучайном равномерном расположении КК (рис. 3, д ) ни на одной горизонтали (вертикали) не находится более одного КК.

Оценка эффективности компенсации помех при помощи алгоритмов на основе оптимального винеровского фильтра и автокомпенсатора с различным расположением КК производилась методом математического моделирования. Обрабатывалась реализация смеси полезного сигнала (прямоугольного импульса) и АШП. В серии опытов направление полезного сигнала изменялось в пределах от -15° до 15° с шагом 5° по азимуту и в пределах от -15° до 15° с шагом 5° по углу места. Для каждого возможного направления полезного сигнала произвольным образом выбирались направления на 10 постановщиков АШП, не попадающих в главный лепесток ДН. СКО всех АШП равнялись 100. Количество опы- тов для каждого направления полезного сигнала равнялось 100. Общее количество опытов для каждого метода составило Nоп = 4900.

Находились оценки следующих критериев качества: коэффициента подавления помех Kп и коэффициента улучшения отношения сигнал– помеха Kу .

к п = 10lg

( Т ²      I

° п.вых ~ 2

V ° п.вых.к /

-0.5 -0.4 -0.3 -0.2 -0.1   0    0.1   0.2   0.3   0.4   0.5

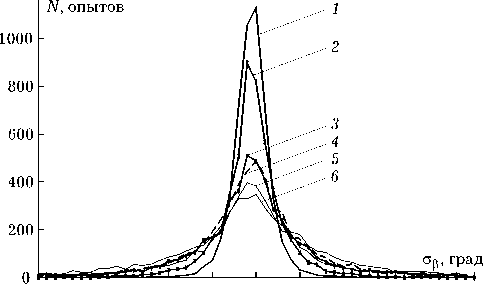
Рис. 4. Распределение отклонения азимута главного лепестка ДН

г)

А(Р,£), дБ

о

20 М^

-5

-15

-20-15 -10 -5 0  5 10 Р, град

-20

о

-10

-20

-30

-40

-50

-60

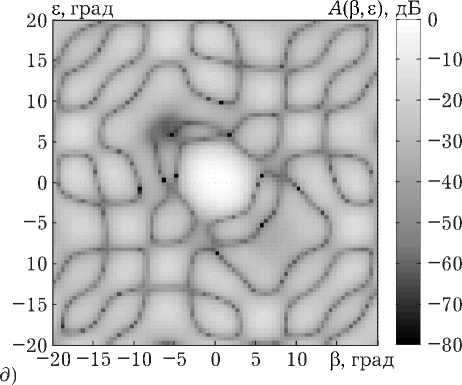
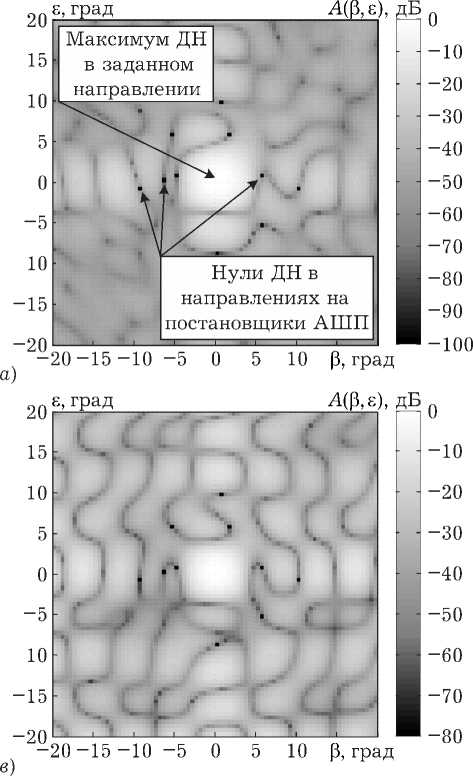
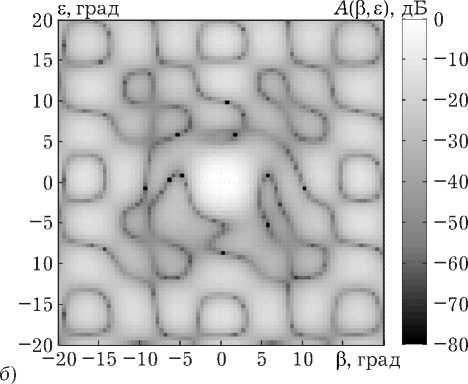
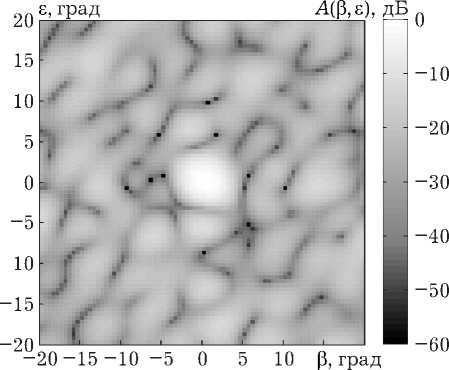
Рис. 5. ДН АФАР при всех рассмотренных способах подавления АШП: а ) решение Винера; б ) равномерное расположение КК; в ) расположение КК по периметру АФАР; г ) расположение КК с увеличением шага; д ) крестообразное расположение КК; е ) квазислучайное расположение КК

е)

На рис. 4 представлены выборочные оценки распределения отклонений максимума главного лепестка ДН от заданного направления при всех выше рассмотренных вариантах подавления АШП. Цифрами на рисунке обозначены: 1 – при использовании винеровского решения; 2 – при использовании автокомпенсатора со случайным расположением КК; 3 – для случая расположения в виде креста; 4 – при равномерно распределенных КК; 5 – при расположении КК по периметру; 6 – при расположении КК с увеличением шага.

Из рисунка видно, что наилучшим по критерию минимума СКО главного луча от заданно- го направления является винеровское решение, а из всевозможных рассмотренных вариантов автокомпенсатора АШП лучшим оказался вариант с квазислучайным расположением КК на полотне АФАР.

Немаловажным показателем качества работы алгоритма является и уровень боковых лепестков ДН K _б . Этот параметр также оценивался методом математического моделирования.

На рис. 5 представлены ДН при всех выше рассмотренных вариантах подавления АШП. Из рис. 5 видно, что во всех рассмотренных методах в направлениях постановщиков АШП формируются глубокие нули ДН. В заданном направлении (направление по нормали к АФАР) формируется максимум ДН. Также можно видеть, что ДН АФАР изменяется в зависимости от способа размещения КК на полотне.

В таблице ниже представлены полученные значения оценок упомянутых выше критериев качества работы алгоритма, построенного на основе винеровского решения, а также автокомпенсатора с различным расположением КК на полотне АФАР.

Из полученных результатов моделирования видно, что из всех рассмотренных алгоритмов компенсации АШП наилучшими показателями

Таблица

Результаты моделирования обладает пространственный фильтр на основе винеровкого решения. Однако его практическая реализация при большом числе элементов решетки (порядка нескольких тысяч) предъявляет невыполнимые на сегодняшний день требования к мощности вычислительных ресурсов.

При использовании автокомпенсатора АШП, реализация которого возможна на базе сигнального процессора (например, ADSP-TS201S TigerSHARC фирмы Analog Devices или ему аналогичного), качество подавления в значительной степени зависит от выбора способа расположения компенсационных каналов на полотне АФАР. Анализ общепринятых критериев качества, а именно: коэффициента подавления помехи, коэффициента улучшения отношения сигнал–помеха, СКО направления главного лепестка ДН АФАР, уровня боковых лепестков, позволяет сделать вывод о том, что квазислу-чайный способ расположения компенсационных каналов является наиболее оптимальным.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках договора № 02.G25.31.0061 от 12 февраля 2013 года (в соответствии с Постановлением Правительства Российской Федерации от 9 апреля 2010 г. № 218).

Метод подавления	к п , дБ	K у , дБ	о в , град	о 6 , град	K б , дБ
Решение Винера	74,61	69,65	0,0407	0,04	–12,84
Автокомпенсатор (см. рис. 3, а)	62,39	62,17	0,4251	0,4509	–10,39
Автокомпенсатор, (см. рис. 3, б)	64,94	64,65	0,1877	0,1758	–11,39
Автокомпенсатор (см. рис. 3, в)	65,35	65,11	0,2103	0,2033	–11,39
Автокомпенсатор (см. рис. 3, г)	65,83	65,70	0,1316	0,1524	–11,97
Автокомпенсатор (см. рис. 3, д)	66,27	66,01	0,0923	0,0927	–12,25

3. Уидроу Б., Стирнз С. Адаптивная обработка сигналов / пер. с англ. М.: Радио и связь, 1989. 440 с.