Влияние теневого сектора экономики на поведение гетерогенных агентов

Д инамические стохастические модели общего равновесия (DSGE-модели) являются теоретическим и прикладным фундаментом современной макроэкономики [1]. Эти модели являются мощным инструментом для разработки монетарной и фискальной политики, при анализе структурных изменений в экономике и объяснении причинноследственных связей между эндогенными переменными. Данный инструментарий используется при исследовании национальных экономик во многих странах [2; 3; 4]. Анализ макроэкономической политики России рассматривается в публикациях [5; 6; 7].

Практически все результаты, полученные с помощью DSGE-моделей, базируются на принципе репрезентативности экономических агентов с рациональными ожиданиями [8; 9]. Данный принцип является одним из самых критикуемых при использовании этих моделей, так как он уравнивает макро- и микроэкономическое поведение агентов. Вместе с тем анализ моделей с гетерогенными агентами является важным как в прикладном, так и в теоретическом аспекте. Во-первых, с помощью этих моделей можно изучать поведение различных групп агентов в рамках подхода общего равновесия. Во-вторых, одной из главных целей при анализе DSGE-моделей является разработка стабилизационной монетарной и фискальной политики. Поэтому возникает вопрос, как разрабатывать подобную политику при разном реагировании на нее индивидуальных агентов.

В предлагаемой публикации исследуется DSGE-модель, в которой агенты испытывают идиосинкратические шоки, связанные, например, с различием в индивидуальных доходах экономических агентов, и системные агрегированные шоки общефакторной производительности. Наличие этих двух видов шоков приводит к ослаблению гипотезы рациональности ожиданий, так как для анализа подобных моделей необходима соответствующая аппроксимация функции распределения доходов агентов [10; 11; 12].

Исследованию моделей при наличии агрегированных неопределенностей (шоков) с гетерогенными агентами посвящен ряд работ [13; 14; 15]. Здесь приведены лишь наиболее значимые работы по исследованию моделей с гетерогенными агентами и наличием агрегированных шоков, в которых источником неоднородности является различие в индивидуальных доходах экономических агентов. Не приводятся публикации по анализу DSGE-моделей с гетерогенными ожиданиями и с гетерогенными предпочтениями агентов. Во всех перечисленных работах присутствует лишь один источник гетерогенности (один идиосинкратический шок), связанный с индивидуальным распределением доходов домашних хозяйств. Главный вывод, вытекающий из этих работ, заключается в том, что динамика агрегированных переменных в основном определяется динамикой первого момента функции распределения запасов капитала, т. е. динамикой агрегированного капитала. Таким образом, распределение запасов капитала среди индивидуальных агентов практически не влияет на макроскопическую динамику. Поэтому представляет интерес исследование макроскопической динамики в DSGE-моделях при наличии нескольких источников идиосинкратических и агрегированных шоков, что является одной из задач предлагаемой публикации. В данной работе анализируется поведение потребителей не только в легальном, но и в теневом секторах экономики. Наличие двух секторов экономики приводит соответственно к двум источникам гетерогенности, связанным с индивидуальным распределением доходов домашних хозяйств в этих секторах. Этим данная публикация отличается от вышеприведенных работ в области исследования моделей с гетерогенными агентами в присутствии агрегированных шоков.

Вместе с тем исследование влияния теневого сектора экономики на макроэкономическую динамику безусловно представляет научный интерес. Так, анализ экономики посредством DSGE-моделей при наличии теневого сектора изучался в работах [16; 17], общим выводом которых является лучшее соответствие полученных теоретических результатов фактическим данным при наличии сектора нелегальной экономики. Все результаты в перечисленных публикациях основаны на принципе репрезентативности агентов. Поэтому результаты по макроэкономической динамике в моделях с теневым сектором экономики и с гетерогенными агентами являются оригинальными. В частности, в предыдущей работе автора [12] показано, что наличие идиосинкратических шоков приводит к снижению корреляции заработной платы с объемом выпуска, по сравнению с корреляцией в моделях с репрезентативными агентами. Однако в цитируемой работе применялась лишь аппроксимация первого порядка для функции распределения доходов индивидуальных агентов. Кроме того, в этой и перечисленных выше публикациях анализируется только теневое (скрытое, формально законное) производство без учета операций в неформальном секторе экономики и в секторе производства домашних хозяйств для их собственного потребления.

Целью предлагаемой публикации является исследование влияния теневого сектора экономики, неформального производства и производства домашних хозяйств для собственного потребления на макроэкономическую динамику в DSGE-моделях и сравнение динамики агрегированных переменных в этих моделях с подобной динамикой в моделях с репрезентативными агентами. Параметры исследуемой модели оцениваются байесовским методом на эмпирических данных экономики России.

Описание модели

В предлагаемой публикации исследуется динамическая стохастическая модель с аг- регированной неопределенностью в виде шоков общефакторной производительности, гибкими ценами и неполными рынками. В модели присутствуют два источника гетерогенности – идиосинкратические шоки доходов домашних хозяйств в легальном и теневом секторах экономики. При этом агенты – домашние хозяйства имеют одинаковые потребительские предпочтения, т. е. они являются ex post неоднородными и ex ante однородными.

При исследовании применяется подход общего межвременного равновесия. Этот подход предполагает, что все экономические агенты (домашние хозяйства, производители, правительство) оптимизируют свою целевую функцию в рамках определенных ограничений. Домашние хозяйства максимизируют дисконтированный ожидаемый поток полезности путем выбора оптимальных траекторий потребления и часов досуга при заданном бюджетном ограничении. Фирмы максимизируют дисконтированный ожидаемый поток прибыли путем выбора в каждом периоде объема производства при заданном технологическом ограничении. Данная модель имеет следующую особенность: результатом ее решения являются структурные поведенческие правила (функции спроса и предложения на продукты и ресурсы) в зависимости от цены.

Росстат подразделяет экономическую деятельность, не наблюдаемую прямыми статистическими методами, на сле- дующие категории: теневое производство, производство в неформальном секторе экономики, незаконные операции (не учитываются Росстатом) и производство домашних хозяйств для их собственного конечного использования. При этом теневое производство является формально законным видом деятельности, но намеренно скрываемым от органов государственной власти в целях уклонения от уплаты налогов или следования законодательным нормам. Неформальный сектор экономики представляет производственную деятельность, осуществляемую незарегистрированными предприятиями сектора домашних хозяйств. Производство домашних хозяйств для собственного конечного использования представляет собой хозяйственную деятельность, в результате которой домашние хозяйства потребляют или капитализируют произведенные ими же товары и услуги.

В описываемой модели учитываются все группы операций, по которым Росстат производит корректировку валовой добавленной стоимости, т. е. теневое (скрытое) производство, операции в неформальном секторе экономики и производство домашних хозяйств для собственного потребления.

В модели рассматриваются три вида агентов – индивидуальные домашние хозяйства, фирмы и государственный сектор. При этом фирмы, действующие на конкурентных рынках, и домашние хозяйства составляют континуальное множество единичной массы (агенту присваивается индекс i ∈ [0,1]). Домашние хозяйства, обладающие определенным запасом собственного и заемного капитала, осуществляют капиталовложения в фирмы по процентной ставке r (ставка арендной платы за капитал). Объем выпуска гомогенного продукта фирмами легального сектора описывается производственной функцией Кобба - Дугласа Yt,r = z^^ht-a, где z - агрегированный шок общефакторной производительности в легальном секторе экономики. В производственной функции K – агрегированное значение капитала (на одного агента), ht r – количество отработанных часов в легальном секторе экономики. Считаем, что теневой сектор обладает более низкой капиталоемкостью по сравнению с легальным, поэтому объем выпуска фирм теневого сектора экономики описывается производственной функцией αu , где z – агрегированный " t, u   z 2, t"t, u            2, шок производительности в теневом секто- ре экономики1, ht u – количество отработанных часов в теневом секторе экономики, au е[0,1]. Отметим, что z^t, z24 явля-

ются экзогенными стохастическими процессами.

При условии единичной цены гомогенного продукта доход фирм легального сектора      экономики      составляет

Rrt = (1 - тР )Ytr, где tf - постоянная ставка налога с прибыли,  tf е (0,1). Учтем также, что фирмы теневого сектора при обнаружении налоговыми органами их деятельности должны будут выплатить сумму szF, где множитель s > 1 является штрафом за неуплату налогов. Тогда суммарный доход фирм составляет Rt=pRD,t+(1 - p)RND,t ’ где p(P е (0,1)) -вероятность обнаружения налоговыми органами теневых операций фирм, R – суммарный доход фирм при обнаружении ими нарушений, аналогично R      – суммарный доход фирм при отсутствии обнаружения ими нарушений. При этом RD,t = (1 — Tf)Yt,r + (1 — STF)Yt,u ,(1)

RND,t = (1 - TF )Yt,r + Yt,u ,

Rt = (1 - Tf )Yt, r + d - PSTF )Yt, u.

Максимизируя прибыль

(h I'haxK ) (nt = Rt — wt,rht,r - wt,uht,u - rtKt) t, r t, u t с учетом (3) и выражений для производственных функций Ytr, Ytu получим урав-

нения

Yw

(1 - a) -F^r =   tP—, ht, r    (1 - Tf )

α _u

Y u =__ w u __при (1 - psT_F ) >  0 ,     (5а)

h t , u

^{(1 -} PS T f )

h tu = ^{0 п}Р^{и (1 -} P^{S t} f ) <  ⁰,

(5б)

Y trr a —^ =

K t

r t      _,

(1 - T f )

где r = r ( K_t , h_{F r}, z^ J - ставка арендной платы за капитал, w_tr = w_F(KK_t , h _r, z ^J , w – заработные платы агентов в легальном и теневом секторах экономики, K – агрегированное значение капитала. Уравнения (5а) – (5б) описывают оптимальный спрос на труд в теневом секторе экономики. Следовательно, если (1 - psv_F ) >  0, спрос на труд в теневом секторе существует до тех пор, пока предельная производительность труда в этом секторе не будет равна предельным издержкам. При (1 - psT_F ) <  0 спрос на труд в теневом секторе отсутствует.

Неоднородные индивидуальные агенты – домашние хозяйства в каждый период времени t максимизируют дисконтированный ожидаемый поток полезности U(c , hit  h , h ) путем выбора опти- it      ,r       ,u it , n мальных траекторий потребления и часов досуга при заданном бюджетном ограничении. Суммарный уровень потребления индивидуального агента описывается функцией с постоянной эластичностью замещения как в работе [16]:

cit = ⁽ a ⁽ cit m^ ^{+ (1 -} a ⁾⁽ cit n ^{Y )V Y} ,    ⁽⁷⁾

,                                               , где переменная c – индивидуальный , уровень потребления агентом товаров и услуг, производимых в легальном, теневом и неформальном секторах экономики. В дальнейшем будем называть эти секторы рыночным сектором. Переменная c – индивидуальный уровень потребления агентом товаров и услуг, производимых в секторе домашних хозяйств, для собственного конечного использования. Параметры а и (1–а) являются весовыми факторами, параметр γ определяет эластичность замещения между двумя видами потребления c и c . Таким образом, задача максимизации ожидаемой дисконтированной суммы значений функции полезности принимает вид

1 Кроме того, в теневом секторе часто используется тот же капитал, что и в легальном.

max

{cit, m ^, cit , n ^, hit , r ^, hit, u ^, hit , nhit , nu }                        (8)

∞

E t S ^{в U (} cit , m , cit , n , hit , r , hit, , u , hit, , nhit , _nu ^).

В выражении (8) E - оператор рациональных ожиданий. Переменные     , it, r ,      ,     – затраты агента на труд it ,u     it, nu    it, n в легальном, теневом, неформальном секторах экономики и в секторе производства домашних хозяйств соответственно. Будем считать, что количество часов       явля- it, nu ется неделимым ресурсом в составе количества часов в секторе производства домашних хозяйств для собственного конечного использования производимых благ h.   . Уровень потребления cit,n зависит от затраченного времени h и применяемого уровня технологии z . Примем, что c=Y= cit,n = z3,thit,n. Соответственно it,nu   it, nu z3,thit,nu•  Вследствие того что трудовой ресурс h     является неделимым, количе- t, nu ство часов, отводимое на досуг индивидуальным агентом,

’ it          it , r     it , u     Tt , n

Домашние хозяйства имеют возможность инвестировать свои активы в физический капитал согласно уравнению k.   . = i.  + (1 - ^)k.   где klt — запас ка- i ,t +1       i , t                      i, t питала индивидуального агента на начало периода, параметр δ является нормой обесценения капитала, i - уровень инвестиций.

Бюджетное ограничение задачи в каждый период времени t для индивидуальных домашних хозяйств, потребляющих товары и услуги, производимые в рыночном секторе экономики, с учетом возможностей заимствования в реальных переменных записывается в виде cit, m + ki, t+1 =(1 - TY)((rt(Kt, ht, r, z1, t) kit +

⁺ wt , r ⁽ Kt , ^ht , r , ^z 1, t ) e4,i,t^hit , r ) ⁺ wt , u^e 5, i , thit , u ⁺

+(1 - £) kit + (1- a) Rit, nu, e4i,t = (1 — p4) + p4e4i,t-1 + ^4i,t, $4i,t ~ N(0, ^4 ) , e5 i, t = (1 - p5) + p5 e5 i, t-1 + $5 i, t,

$5i,t ~ N(0,^52) , ki,t+1 >-B, B > 0.

В бюджетном ограничении (9) R    – доход индивидуального агента от

,nu’ производства в неформальном секторе экономики. В соответствии с соображениями, согласно которым получены уравнения (1) - (3), Rit,nu = (1 -psTY)z3,thit,nu . Параметр ® e (0,1) характеризует долю издержек от дохода R    при изготовлении t, nu продукции в неформальном секторе экономики. В ограничении (9) предполагается различие в трудовом статусе и, как следствие, в заработных платах индивидуальных агентов в легальном w = w e и it, r      t, r 4, i, t теневом секторе w = w e . Это t, u      t, u 5, i, t различие обусловлено идиосинкратическими шоками e и e , подчиняю щимися авторегрессионному процессу первого порядка. В бюджетном ограничении (9) τ – ставка налога на доход физи ческих лиц, Ту e (0,1). В дальнейшем для упрощения будем считать количество отработанных часов в отдельных секторах одинаковым для всех агентов1, то есть hit, r = ht, r, hit,u = ht,u , hit,n = ht,n , hit,nu = ht,nu . Ограничение на запасы капитала k ≥ -B (ограничение на заимствования) обеспечивает частичное страхование агентов против рисков уменьшения доходов и неотрицательность потребления. Более подробно с ограничением на заимствования можно познакомиться в работе [19].

Экзогенные агрегированные шоки общефакторной производительности z , z , z являются серийно коррелирован- ными и изменяются в соответствии с уравнениями zi,t = (i - A) + pizi,t-i + ^i,t, z2,t = (i — p2) + P2z2,t-i + $2,t, z3,t = (i — p3) + p3Z3,t-i + ^3,t , где ^t ~ N(0,ст;2), i=1,2,3 и ^i - соответствующие дисперсии.

Однопериодная функция полезности, используемая в предлагаемой публикации, основанная на вышеназванных предпосылках, имеет вид

U ⁽ cit ’ hit , r ’ hit , u ’ hit , n ) =

Bm ⁽ lt ⁾ⁱ - ^P  Bu^u*

= ln( c ) — 0 h    + ^m t ---,--- ,     ⁽¹³⁾

v it>     t,nu       i — p         i + z где суммарный уровень потребления c определяется равенством (7), lt - количество часов досуга, параметр Bm определяет предпочтение досуга, параметры Θ и Bu определяют предпочтение труда в неформальном и теневом секторах экономики соответственно. Параметры p, Z — об- ратные эластичности предложения труда в соответствующих секторах экономики. Заметим, что функция полезности (13) является возрастающей по переменной c и удовлетворяет условиям

d U (.) lim  — ⁷

∂ c

C it ^ ^{0 it}

и

lim ^cit ^→∞

d U (.) ∂ c_it

= 0 '

С учетом этих свойств по- ложительность потребления всегда опти- мальна.

Для абстрагирования от ограничения k ≥ -B в виде неравенства следует заменить это ограничение стандартным добавлением в условие максимизации (8) штрафной функции [15] вида

^{P (} k i , , + i ) = ^{П ex}P^{( —} П о ⁽ k i , , + i ⁺ B )) ^— П 2 ⁽ k i , , + i ⁺ B ) ^{, (14)} П 0

где η ,η ,η - параметры штрафной функции. Условие максимизации (8) в этом случае примет вид max

{ c    c h h h h     }

• it , m , it , n , it , r , it , u , it , n it , nu¹

∞

• E, ^ P ^{U ( c}it , _m , ^cit , n ’ hit , r , hit , u ’ hit , nhit nu ) t = 0                                                                   ,

  
  

  _-

  
  

—^ p ( k , t + i )•

Кроме домашних хозяйств и фирм в модели присутствует третий агент – государство. В каждом периоде времени t государство аккумулирует налоги для финансирования государственных расходов. Для упрощения абстрагируемся от государственного долга, трансфертов и предположим, что в каждый момент времени бюджет государства сбалансирован. В этом случае бюджетное ограничение со стороны государства можно записать в виде i gt = Ту J (rk. + w e h + psY    )di +

Y¹ t it t , r 4, i , t it , r        it , nu

⁺ т ( Y + psY ) .                         ⁽¹⁶⁾

F t , r        t , u'

Остановимся более подробно на решении задачи оптимизации. Задача оптимизации (15) решается в данной работе методами теории возмущений первого и второго порядка [14; 18]. Чтобы решить эту задачу, агенты должны уметь прогнозировать будущие цены труда и капитала. Для этого необходимо знать стохастический процесс, описывающий эволюцию агрегированного капитала. Стохастические свойства запасов агрегированного капитала зависят от распределения его среди всех индивидуальных агентов, поэтому для решения задачи оптимизации (15) необходима соответствующая аппроксимация функции распределения доходов (запасов капитала).

В предлагаемой публикации используется один из самых популярных подходов P. Krusell and A. Smith [13], которые предложили аппроксимировать распределение доходов дискретным и конечным набором моментов m = (m^, m2 ,•••, mi), где i – порядок момента. При этом они показали, что в модели с одним источником гетерогенности для функции распределения доходов достаточно аппроксимации первого порядка. Поскольку исследуемая модель характеризуется наличием двух источников гетерогенности, в предлагае- мой публикации рассматривается аппроксимация распределения доходов индивидуальных агентов первого и второго порядков.

Основной целью подхода P. Krusell and A. Smith является получение агрегированных и индивидуальных поведенческих функций. Для этого при аппроксимации первого порядка ( i=1 ) динамика функции распределения запасов капитала индивидуальных агентов заменяется динамикой ее первого момента, т. е. воспринимаемым агентами законом изменения агрегированного капитала. Функциональную форму этого закона можно представить в виде

K = b 0 + b_KK_t - 1 + b z _t ( z^_t - z 1 ) +

+ b z ₂( z 2, t - z 2 ) ,                                      (17)

где z_x , z ₂ — стационарные детерминированные состояния шоков производительности z^,, z₂ ,, параметры b₀ , b_K , b,, b_z2 характеризуют убеждения агентов относительно изменения агрегированного капитала и обновляются при каждой итерации [15].

При аппроксимации второго порядка воспринимаемый агентами закон изменения агрегированного капитала и соответствующих моментов записывается в виде

K ‘= f _;( K , z 1 , z 2 , M ke4 ,

M ke 5 , M_k 2 ; Z ),                            (17а)

M k 2 = f _;( K , z 1 , z 2 , M ke 4 , M ke 5 , M k 2 ; Z ),

M k _A = f 2 ( K , z _x , z 2 , M ke 4 , M ke 5 , M_k 2 ; Z ),

Mke 2 = fЛK, zp z 2, Mke 4, Mke 5, Mk-Z), где   M i2, Mkel, Mke2 — соответствующие моменты второго порядка, Z, Z, Z, Z — векторы коэффициентов перед соответствующими переменными, переменные со штрихом относится к периоду t+1, временные индексы опущены.

Пошаговая реализация алгоритма P. Krusell and A. Smith применительно к исследуемой модели при аппроксимации первого порядка выглядит следующим образом.

• 1.    Задаются начальные значения вектора параметров убеждений агентов b

• 2.    Генерируется временная последовательность агрегированных и идиосинкратических шоков длиной T .

• 3.    Для заданного вектора параметров b и закона изменения агрегированного капитала (17) решается задача оптимизации (15) с функцией полезности (13) и ограничениями (7) – (12) с учетом (4) – (6), (17) для индивидуального агента. Результатом решения задачи оптимизации являются поведенческие функции (правила) для      индивидуальных      агентов

• 4.    Используя полученные на третьем шаге оптимальные поведенческие функции (правила) для индивидуальных агентов, с помощью метода Монте-Карло проводится имитационное моделирование индивидуальных запасов капитала для совокупности N агентов. Агрегируя на каждом периоде симуляции запасы капитала индивидуальных агентов, получаем временной ряд Kt .

• 5.    С помощью уравнения регрессии для агрегированного капитала K находит

• 6.    Для обновления закона изменения агрегированного капитала задается

• 7.    Повторяются шаги с третьего по шестой до тех пор, пока норма вектора разности b new - b не будет превышать заданную величину ошибки.

из компонент b b b b , запасов капи- U K z 1 z 2

тала k для N индивидуальных агентов. Начальные значения задаются из условий максимальной скорости схождения алгоритма.

k ' = k ( z 1 , z ₂, z ₃, e ₄, e ₅, K ') 1 .

ся вектор параметров b .

~ вектор параметров bnew для следующей возможной итерации по правилу ~~ bnew = λb + (1 -λ)b, где λ∈[0,1] - параметр обновления.

При аппроксимации второго порядка обновление векторов коэффициентов

• ¹    Переменная со штрихом относится к периоду t+1 , индексы – временные и индивидуальных агентов – опущены.

Z , Z , Z , Z происходит через алгоритм агрегации. Итерации продолжаются до тех пор, пока ||Z j ( • ) -Z j ^{- 1}( » )|| <  s , где || Z || -норма вектора, составленного из коэффициентов Z , Z , Z , Z , s — заданная величина ошибки.

При решении задачи оптимизации индивидуальные агенты обладают рациональными ожиданиями в слабой форме [8]. Поясним это подробнее. Пусть I t , h - информационное множество, доступное агенту h в конце периода t , включающее в себя все структурные характеристики анализируемой системы. Множество I _th содержит текущие и предшествующие значения всех переменных модели и реализации всех случайных величин (шоков) в текущем и прошлых периодах. Пусть E _t , _h u _{t +} k – субъективное ожидание (прогноз), сформированное агентом h относительно значения, которое примет переменная u в период времени t+k, k >  1. Пусть также E [ u _{t +} k | I_t , _h ] - объективное, т. е. вычисленное в силу модели, связывающей в конечном счете решения всех агентов, ожидаемое значение u_t+k при условии I_t , _h (через E здесь обозначен оператор условного математического ожидания). В нашем исследовании объективные и субъективные ожидания не совпадают ввиду использования агентами при прогнозировании цен ограниченного аппроксимацией функции распределения доходов информационного множества, то есть E _t , h u t ₊ k = ^{E [ u} t + k | I t , h ^{] + s} t , h , где ^E[ S , h I I t , h ^] = °- В результате функционирования алгоритма P. Krusell and A. Smith происходит минимизация ошибки ^S t , h •

Условия равновесия и решение модели

Идея экономического равновесия заключается в том, что каждый из агентов в модели предлагает свой план величины спроса и предложения на продукты и ресурсы [20]. Этот план условный, так как он зависит от значений информационных переменных (цен на продукты и ресурсы) и имеет внешнее ограничение относительно значений агрегированных цен (w , w , r ).

• t , r t , u t

В процессе взаимодействия агентов их планы согласовываются так, чтобы выполнялись включенные в модель материальные и финансовые системные балансовые соотношения.

Таким образом, применительно к исследуемой модели, общее равновесие устанавливается в результате:

оптимизации: агенты – домашние хозяйства решают задачу максимизации (15) при ограничениях (7) – (12) и заданных значениях w w r (4) – (6) и вос-t, r ’ t, u ’ t принимаемом агентами законе изменения агрегированного капитала (17). Результатом решения задачи оптимизации являются поведенческие функции агентов, зависящие от агрегированных шоков общефакторной производительности, идиосинкратических шоков, запасов капитала агентов, и согласованные с законом изменения агрегированного капитала (17);

равновесия на рынке товаров и услуг:

c ( k, Z j , z ₂, z 3 , e ₄, e ₅, K ') + 1

> di = Y_r +

+ k ( k , Z j , z 2 , z 3 , e 4 , e ₅, K )

+Yu + (1 - ^) K, где c (•), k '(•) — поведенческие функции агентов; операция интегрирования заключается в суммировании по соответствующим функциям всех индивидуальных моделируемых агентов;

ценового фактора: заработные платы и процентная ставка определяются из условий максимизации прибыли фирм (4) – (6);

агрегирования факторов производства : Kt = j ki tdi, d , h_t , _r = j h_it , r di , ^ht , n = j hit , n^di , ht , nu = j hit , n^{di -}

Максимизация (15) по отношению к (7), (9) и с учетом уравнений (4) – (6), (10) – (14), (17) приводит к системе уравнений для индивидуального агента исследуемой модели. Система уравнений модели, явля- ющаяся результатом реализации алгоритма P. Krusell and A. Smith и соответствующая состоянию общего равновесия, выглядит следующим образом:

ct = ( a ( ct, m ) Y + (1 — a )( ct , n ) Y )1/ Y ;	(18)
/ — 1 acm , t              ,	(19)
( acm,t + (1 - a ) c Y , t )     t где λ - множитель Лагранжа;
(1 — a ) cn — 1       1        -o n , t                      p =   + B l    ;	(20)
( acm , t + (1 - a ) c n ,t )    lt    mt
0 = ^ t (1 — ps T Y ) z ■ 3, t ;	(21)
A t = Et A t + 1 + ^ (1 + (1 — T Y ) г, — S ) ;	(22)
lt = 1 — hr,t — hn,t — hu,t ;	(23)
lt - 1 =— B l .- p + A (1 — Tv ) w  ,; t      mt      t     Y  m , t l — 1 =— B l — p + A w   — B h Z ; t        mt       t u , t    u u , t	(24)
(25)
z^t (1 — FF )(1 — a ) K a h ta= wt , r ;	(26)
z 2, t (1 — Ps T F ) = wt , u ;	(27)
z 1, t (1 — T f ) a K'1 ht — = r, ;	(28)
ct , m + Kt + 1 = (1 — YY )(( rt ( Kt , ht , r , z 1, t ) Kt	+

+ wt , r ( Kt , ht , r , z 1, t ) ht , r ) + wt , uht , u + (1 S ) Kt +
+ (1 — ^ Rt , nu ’	(29)
Rt , nu = (1 — ps T Y ) z 3, t	h     ;             (30) t , nu
Y     = z  h    ;	(31)
t , nu     3.t t . nu
'h 1 — ' . Y t , r = z1,tKt ht , r ;	(32)
Yt , u = z2,tht,u ;	(33)
c   = z   h   ; n , t     3, t t , n	(34)
g, = t ( r K + w h g t      Yy t t     t , r t , r	+ psY   ) + t , nu
,          , + t ( Y  + psY ); F t , r       t , u	,         ,    (35)
z 1, t = (1 — P 1) + P 1 z 1, t —	i + ^ 1, t ;               (36)
z 2, t = (1 — p 2) + p 2 z 2, t	— 1 + ^ 2, t ;         (37)
z 3, t = (1 — p 3) + p 3 z 3, t-	_ 1 + ^ 3, t .            (38)

Все переменные системы уравнений (18) – (38) являются агрегированными пе-

ременными. Эта система уравнений описывает модель, параметры которой связаны с предпочтениями гетерогенных (не репрезентативных!) агентов. Реализация алгоритма P. Krusell and A. Smith для анализа модели с гетерогенными агентами осуществлялась в программном пакете Matlab . При этом второй шаг алгоритма, т. е. решение задачи оптимизации для индивидуального агента, оценка параметров модели и окончательная реализация модели, осуществлялись в программном пакете Dynare ¹. При аппроксимации функции распределения запасов капитала моментами первого порядка решение уравнений модели выполнялось с помощью приближения первого порядка теории возмущений. Соответственно при аппроксимации функции распределения моментами второго порядка решение уравнений модели осуществлялось с помощью приближения второго порядка. Окончательная реализация модели происходила при значениях параметров, полученных после реализации алгоритма P. Krusell and A. Smith.

Оценка параметров модели

Параметры исследуемой модели при каждой итерации оценивались с помощью метода Байеса на эмпирических данных российской экономики. Байесовский статистический подход можно охарактеризовать как «обучающий» процесс, при котором вектор наблюдаемых переменных Υ ис- пользуется для получения информации об апостериорной функции плотности вероятностей f (^ | Y) распределения вектора параметров модели ϑ при заданной априорной функции плотности вероятности f (3) и функции правдоподобия L(^; Y).

Байесовский статистический подход бази- руется на теореме Байеса [21]:

f ( . | Y ) = ML&Y1 , f ( Y )

где f ( Y ) — функция маргинального правдоподобия (нормализованная константа).

Поскольку функция правдоподобия находится при решении DSGE-модели, можно определить вид числителя в (39), в то время как знаменатель является константой (не зависит от $ ). Как уже отмечалось выше, при каждой итерации алгоритма P. Krusell and A. Smith происходит оценка параметров модели на основе (39) путем нахождения апостериорного максимума. При оценке модели использовались квартальные данные для российской экономики, с 1-го квартала 2003 г. по 4-й квартал 2015 г. Анализировались пять (по числу экзогенных шоков) эндогенных макроэкономических переменных – агрегированный, скорректированный ВВП (включая теневой сектор, сектор неформального производства и сектор домашних хозяйств), ВВП теневого сектора, зарплата в легальном секторе экономики, инвестиции, потребление домашних хозяйств¹. Все переменные выражены в единицах на душу населения² и рассчитывались в постоянных ценах 2003 г. Для данных по ВВП теневого сектора экономики использовались годовые показатели корректировки валовой добавленной стоимости на экономические операции, не наблюдаемые прямыми статистическими методами³. Для перевода годовых показателей корректировки (процент к валовой добавленной стоимости) теневых операций в квартальные использовался аппарат сплайн-аппроксимации с последующей коррекцией полученных данных временных рядов [12].

Несколько параметров модели фиксировалось [22; 23; 24]. Коэффициенты в штрафной функции выбраны из условий устойчивости и максимальной скорости сходимости алгоритма: щ = 0,4 ,п = 0,3, П = 0,4 . Начальные значения коэффициентов в (17) для приближения первого порядка b0 = 1,4, bK = 0,6, bz = 0,95 и значение параметра Л = 0.5 также выбраны из условий максимальной скорости сходимости алгоритма. Параметры а = 0,36, аи = 1, 8 = 0,025, в = 0,99. Эти значения параметров наиболее часто используются при калибровке DSGE-моделей росcийской экономики [5; 6; 25]. Для упрощения кредитный лимит B=0 (отсутствие чистого долга). Число моделируемых агентов N = 1000, длина временной последовательности шоков T = 10000.. Параметр s принят равным 1,3, параметр p=0,1 исходя из штрафов за неуплату налогов. Налоговые ставки т = 0,13, т = 0,2 (основные ставки)4. Коэффициент а в уравнении (7) принят равным 0,830 как среднее значение из данных по корректировке валовой добавленной стоимости на производство домашних хозяйств для собственного потребления.

Остальные параметры оценивались с помощью метода Байеса. Априорные распределения для всех параметров, как и апостериорные распределения, представлены в табл. 1. Для сравнения приведены данные для оцененных параметров в рамках модели с репрезентативными агентами. Отметим, что оценка всех параметров в табл. 1 происходила во время последней итерации на основе апостериорного максимума с помощью алгоритма случайного блуждания Метрополиса – Хастингса [21].

Далее охарактеризуем результаты моделирования влияния теневого, неформального сектора и сектора домашних хозяйств на динамику стохастической модели с неоднородными агентами.

4 Для упрощения косвенные налоги не учитываются, что не влияет на общность рассуждений и полученные результаты.

Таблица 1

Оценка параметров исследуемой модели с гетерогенными и репрезентативными агентами по данным российской экономики

Параметр	Априорное распределение			Апостериорное распределение
				Модель с гетерогенными агентами		Модель с репрезентативными агентами
	Тип	Среднее	Стат. отклонение	Среднее	t-stat	Среднее	t-stat
γ	Гамма	1,831	0,500	1,643	4,481	1,513	4,545
Bu	Гамма	1,921	0,500	2,458	11,897	2,532	13,161
Bm	Обр. Гамма	0,250	0,500	0,178	7,231	0,152	7,694
ρ	Обр. Гамма	0,300	0,500	0,261	7,613	0,373	8,604
Θ	Бета	0,100	0,500	0,132	6,645	0,142	6,641
ζ	Бета	0,14	0,200	0,291	1,741	0,413	1,787
ρ 1	Бета	0,900	0,200	0,667	4,787	0,665	4,981
ρ 2	Бета	0,900	0,200	0,783	4,254	0,815	21,654
ρ 3	Бета	0,900	0,200	0,862	11,787	0,812	66,765
ρ 4	Бета	0,900	0,200	0,662	9,281	0,612	61,141
ρ 5	Бета	0,900	0,200	0,612	6,265	0,667	31,234
σ 1	Обр. Гамма	0,040	1,000	0,066	8,498	0,049	8,114
σ 2	Обр. Гамма	0,040	1,000	0,019	7,441	0,021	7,123
σ 3	Обр. Гамма	0,040	1,000	0,011	3,361	0,013	4,554
σ 4	Обр. Гамма	0,040	1,000	0,016	2,356	0,012	3,427
σ 5	Обр. Гамма	0,040	1,000	0,013	3,234	0,011	3,567
Логарифм маргинального правдоподобия				410,647		396,451

Результаты моделирования

С

ущественным результатом оценки параметров является то, что функция правдоподо-

бия (маргинальное правдоподобие) модели с гетерогенными агентами имеет большее значение по сравнению с аналогичной функцией для модели с репрезентативными агентами (табл. 1), т. е. исследуемая модель более адекватно описывает эмпирические данные российской экономики.

Данные апостериорного распределения свидетельствуют о существенном различии для параметров ρ и ς сравниваемых моделей. Эти параметры связаны с обратными эластичностями предложения

труда в легальном и теневом секторах экономики. Из табл. 1 видно, что значения этих параметров для модели с репрезентативными агентами намного больше, чем для модели с гетерогенными агентами, т. е. неоднородность распределения запасов капитала среди агентов способствует повышению эластичности предложения труда в соответствующих секторах экономики. Также следует отметить, что эластичность замещения γ между двумя видами потребления c и c для модели с гетерогенными агентами выше по сравнению с аналогичной эластичностью для модели с репрезентативными агентами. Значения

остальных параметров сравниваемых моделей различаются незначительно.

Как уже отмечалось, одной из целей предлагаемой публикации является сравнение динамики агрегированных переменных в исследуемой модели с двумя идиосинкратическими шоками с подобной динамикой в моделях с репрезентативными агентами. В табл. 2 приведена статистика агрегированных переменных: суммарного потребления с, потребления в рыночном секторе c и секторе домашних хозяйств c при одинаковых симуляциях шоков1 общефакторной производительности. Из данных таблицы следует, что при наличии в исследуемой модели идиосинкратических шоков игнорирование моментов выше первого порядка в функции распределения запасов капитала может привести к значительной ошибке. В большей степени это относится к суммарному потреблению и потреблению в рыночном секторе экономики.

Стандартные отклонения этих переменных при аппроксимации второго порядка отличаются от отклонений в модели с репрезентативными агентами. Полученные оригинальные результаты выявляют отличие в поведении агрегированных переменных в исследуемой модели с двумя идиосинкратическими шоками от динамики агрегированных переменных в моделях с одним источником гетерогенности [13; 14; 15]. Данное отличие можно объяснить тем, что в модели с двумя источниками гетерогенности агенты подвержены повышенному риску получения дохода. Таким образом, при анализе динамики агрегированных переменных необходимо учитывать не только моменты первого порядка функции распределения запасов капитала, но и моменты второго порядка.

Таблица 2

Влияние идиосинкратических шоков на агрегированные переменные

Статистика агрегированной переменной*	Модель с репрезентативными агентами**		Модель с идиосинкратическими шоками**
	Аппроксимация первого порядка	Аппроксимация второго порядка	Аппроксимация первого порядка	Аппроксимация второго порядка
Среднее значение с (%СС)	0	–0,13	0	–3,128
Стандартное отклонение с	0,02	0,02	0,077	0,087
Среднее значение c  (%СС)	0	–0,11	0	–2,324
Стандартное отклонение c	0,013	0,013	0,067	0,074
Среднее значение c (%СС)	0	–0,06	0	–1,543
Стандартное отклонение c	0,011	0,011	0,012	0,012

* Переменные усреднены по размеру популяции индивидуальных агентов и выражены в отклонениях от стационарного состояния (СС).

** При аппроксимации функции распределения запасов капитала моментами первого порядка реализация моделей с репрезентативными и гетерогенными агентами осуществляется приближением первого порядка теории возмущений. Соответственно при аппроксимации моментами второго порядка – приближением второго порядка.

Одним1 из основных инструментов анализа DSGE-моделей является исследование поведения функций импульсного отклика. На рис. 1 показано влияние одномоментного положительного шока производительности в легальном секторе эконо- мики на переменные исследуемой модели. Приведенные результаты, в принципе, являются ожидаемыми. Положительный шок производительности в легальном секторе экономики приводит к возрастанию всех основных показателей, в том числе повышению потребления для собственного конечного использования в секторе домашних хозяйств (переменная hn). В то же время выпуск в теневом секторе экономики уменьшается (переменная hu). При этом следует отметить более высокую степень

затухания отклика спроса на труд в легальном секторе экономики (переменная hr ) по сравнению с персистентностью от-

клика остальных переменных.

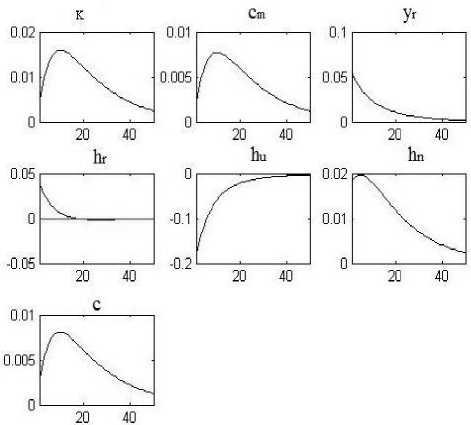
Рис. 1. Влияние положительного шока общефакторной производительности в легальном секторе экономики на переменные исследуемой модели*

* Параметры модели указаны в тексте и табл. 1. Величина шока равна одному стандартному отклонению.

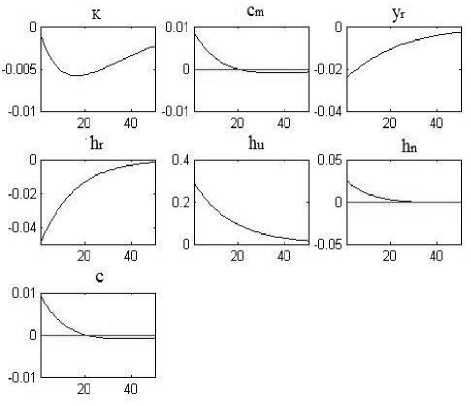
Рис. 2. Влияние положительного шока общефакторной производительности в теневом секторе экономики на переменные исследуемой модели*

* Параметры модели указаны в тексте и табл. 1. Величина шока равна одному стандартному отклонению.

Положительный одномоментный шок производительности в теневом секторе экономики, напротив, приводит к возрастанию объема выпуска в этом секторе и к снижению спроса на труд в легальном секторе экономики (рис. 2). Объем выпуска в легальном секторе ( yr ) и запасы капитала ( k ) также снижаются. При этом суммарный и рыночный уровни потребления возрастают. Уровень потребления домашних хозяйств, производящих блага для собственного потребления, также возрастает. Приведенные результаты свидетельствуют о позитивном влиянии (ниже определенного предела) теневых секторов (включая неформальный сектор экономики и сектор производства домохозяйств) на минимизацию темпов снижения экономических показателей во время рецессий, особенно для развивающихся экономик. Таким образом, теневая экономика является одним из факторов противодействия рецессии, так как деньги, зарабатываемые в теневом секторе, увеличивают потребительский спрос и занятость населения. Но негативным фактором полученного результата является уменьшение сбора налогов для финансирования госрасходов. Поэтому задачей государства является уменьшение влияния этих секторов на макроэкономику за счет увеличения позитивной роли легального сектора.

Интересно проанализировать влияние повышения налоговых ставок на динамику объема выпуска в легальном и теневом секторах экономики. На рис. 3 показано изменение динамики объема выпуска в легальном секторе экономики при повышении ставки корпоративного налога с прибыли на три процентных пункта. На рис. 4 приведено аналогичное изменение динамики объема выпуска в теневом секторе экономики. Результаты говорят сами за себя: объем выпуска в легальном секторе уменьшается, а в теневом возрастает. Исключение составляет период симуляций, который соответствует временному отрезку 2013– 2015 гг. в статистических данных и приходится на период резкого спада экономики. Вероятнее всего эффект спада экономики превалирует над эффектом повышения налоговых ставок.

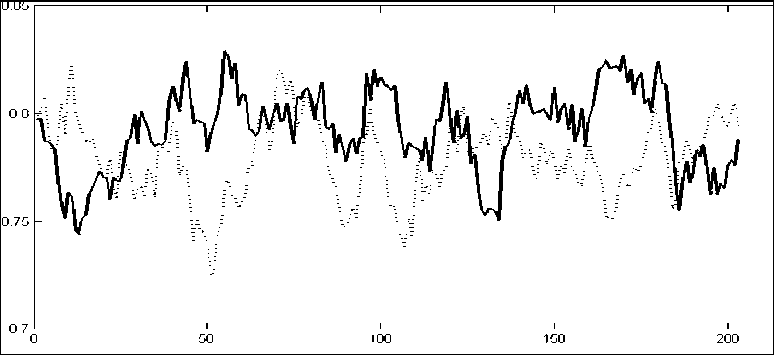
Рис. 3. Динамика объема выпуска (нормированного к суммарному объему выпуска) в легальном секторе экономики при значении ставки налога с прибыли корпораций 0,20 (сплошная линия) и 0,23 (точечная линия)*

* Остальные параметры модели указаны в тексте и табл. 1. По горизонтальной оси отложен период симуляций исследуемой модели.

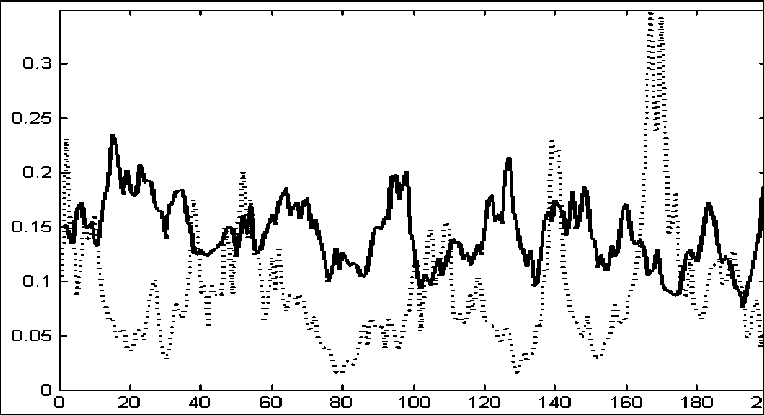
Рис. 4. Динамика объема выпуска (нормированного к суммарному объему выпуска) в теневом секторе экономики при значении ставки налога с прибыли корпораций 0,23 (сплошная линия) и 0,20 (точечная линия)*

* Остальные параметры модели указаны в тексте и табл. 1. По горизонтальной оси отложен период симуляций исследуемой модели.

На рис. 5 приведено изменение динамики объема выпуска в секторе домашних хозяйств, производящих блага для собственного потребления, при повышении ставки налога на доход физических лиц на пять процентных пунктов. Из приведенных результатов следует, что с увеличением налоговой ставки потребление домашних хозяйств, производящих собственные блага, увеличивается. Исключение, как и в предыдущем случае, составляет период симуляций, приходящийся на временной отрезок резкого спада экономи- ки. Пока неясно, связано это со статистической ошибкой или, действительно, со снижением потребления собственных благ домашними хозяйствами. Отметим также, что изменение динамики объема выпуска в неформальном секторе экономики с изменением ставки налога на доход физических лиц аналогично тем же процессам, происходящим в секторе домашних хозяйств, что отражено на рис. 5. Поэтому отдельный график по неформальному сектору экономики не приводится.

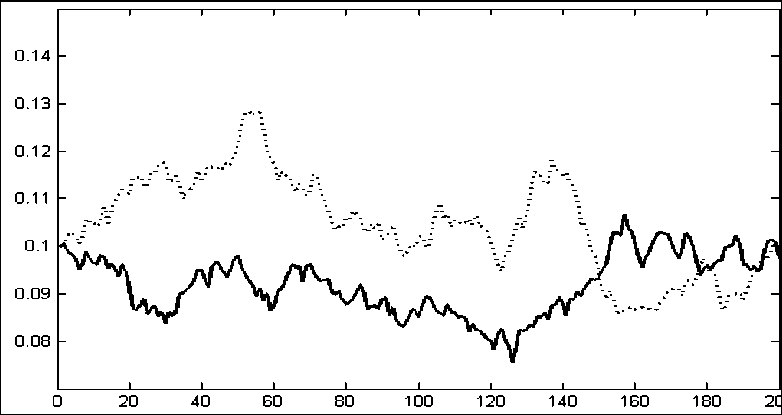
Рис. 5. Динамика объема выпуска в секторе домашних хозяйств (нормированного к суммарному объему выпуска), производящих блага для собственного потребления, при значении ставки налога на доход физических лиц 0,13 (сплошная линия) и 0,18 (точечная линия)*

* Остальные параметры модели указаны в тексте и табл. 1. По горизонтальной оси отложен период симуляций исследуемой модели.

Заключение

Представлены результаты исследования влияния теневого, неформального и сектора домашних хозяйств, производящих блага для собственного потребления, на макроэкономическую динамику в DSGE-модели. При этом применялся алгоритм аппроксимации динамики функции распределения запасов капитала индивидуальных агентов – динамикой ее первого и второго моментов. Параметры модели при каждой итерации алгоритма оценивались с помощью метода Байеса на статистических данных российской экономики. Оригинальным результатом является установление необходимости учета не только моментов первого порядка функции распределения запасов капитала индивидуальных агентов, но и моментов второго порядка при анализе динамики агрегированных переменных. Поведение функций импульсного отклика основных переменных модели подтверждает факт позитивного влияния теневой экономики (ниже определенного предела) на минимизацию темпов снижения экономических показателей во время рецессий, особенно для развивающихся экономик. Также следует отметить, что неоднородность распределения запасов капитала среди агентов способствует повышению эластичности предложения труда в соответствующих секторах экономики.

Предлагаемая модель представляет интерес, как с методологической точки зрения, так и с практической – для анализа секторов экономики, не наблюдаемых прямыми статистическими методами.