Влияние толщины металлического слоя на характеристики SH-волн в структурах Me/ZnO/Me/алмаз и Me/AlN/Me/алмаз

Введение. Устройства акустоэлектроники имеют ограниченные размеры, и при их разработке актуальной проблемой становится учет отражения и преломления упругой волны от границы кристаллической пластины либо от зоны контакта двух различных сред [1]. Более сложная ситуация складывается в многослойных структурах, где необходимо поочередно учитывать границы между всеми кристаллическими слоями. В данном случае может происходить трансформация типа упругого колебания либо возбуждение поверхностной волны при отражении объемной волны от межслойного интерфейса [2]. В настоящее время появилось много экспериментальных и теоретических исследований массовой чувствительности различных акустоэлектронных устройств на основе многослойных пьезоэлектрических структур, работающих на поперечных и продольной толщинных модах упругих колебаний [3–5]. В частности, существуют работы, в которых сдвиговые колебания резонаторов, созданных на подобных структурах, были использованы для разработки биосенсоров [6]. В сенсорах, созданных на основе слоистой пьезоэлектрической структуры, толщина электродов часто сопоставима с толщиной пьезоэлектрической пленки, и, следовательно, металлическими слоями нельзя пренебрегать. Тем более что такие металлы, как золото или платина, которые часто используются в сенсорах для различных биохимических применений, обладают значительными значениями акустического импеданса [7]. Однако исследования влияния массовой нагрузки пока не дают ответ на вопрос об основных причинах изменения значений фазовой скорости упругой волны в слоистой структуре. Таким образом, учет влияния толщины металлических слоев на изменение дисперсионных характеристик упругой волны в многослойной пьезоэлектрической структуре имеет ключевое значение для оптимизации конструкции и повышения чувствительности сенсоров на подобных структурах [8].

В настоящей работе выполнено компьютерное моделирование влияния массовой нагрузки в виде металлических слоев на дисперсионные характеристики мод упругой волны Лява в пьезоэлектрических слоистых структурах с оксидом цинка на алмазе (Me/ZnO/Me/алмаз) и нитридом алюминия на алмазе (Me/AlN/Me/алмаз). Данные материалы обладают набором таких свойств, как большие значения коэффициента электромеханической связи у пьезоэлектриков и значительные величины фазовых скоростей объемных волн и поверхностной акустической волны в алмазе. Благодаря этим особенностям рассматриваемые материалы широко используются при разработке различных акустоэлектронных устройств. В качестве материалов металлических слоев были выбраны алюминий, молибден, платина в виде напыленной тонкой пленки, т. е. металлы, наиболее часто применяющиеся при изготовлении электродов [9]. Результаты выполненного моделирования могут быть использованы при разработке различных акустоэлектронных устройств, в том числе используемых в качестве компонентов электронной базы ракетно-космической техники.

Теоретические основы распространения упругих волн в слоистой пьезоэлектрической среде.

Упругие волны малой амплитуды распространяются в невозмущенном внешними воздействиями пьезоэлектрическом кристалле. Уравнение движения, уравнение электростатики и уравнения состояния пьезоэлектрической среды имеют вид [10]

ее

^р0 U A = ^Т AB , B ; D M , M = ⁰ ;              (1)

ТAB = c ABCDПCD - eMABEM ; DM = £MnEN + eMABПAB , где ρ0 – плотность кристалла в недеформированном состоянии; UA – вектор динамических упругих смещений; τAB – тензор термодинамических напряжений; DM – вектор электрической индукции; ηCD – тензор малых деформаций; cAEBCD , eMAB , εηMN – упругие, пьезоэлектрические и диэлектрические постоянные второго порядка. Для упругих смещений и электрического потенциала в виде плоских монохроматических волн малой амплитуды система уравнений (1) записывается в виде уравнения Грина–Кристоффеля, которое необходимо решить для каждой используемой среды слоистой структуры [11].

Введем рабочую ортогональную систему координат, в которой ось X ₃ направлена вдоль внешней нормали к поверхности слоя, а ось X ₁ совпадает с направлением распространения волны (рис. 1). Распространение упругой волны в такой системе должно удовлетворять соответствующим граничным условиям. Граничными условиями, в частности для четырехслойной структуры «металл – пьезоэлектрик – металл – диэлектрическая подложка» (рис. 1, а ), являются: равенство нулю нормальных компонент тензора напряжений на границе раздела «металл–вакуум»; равенство нормальных компонент тензора напряжений на границе раздела «металл–пьезоэлектрик»; равенство векторов смещения; равенство нулю волны электрического потенциала [12]:

т ? * 1 , = 0;

x 3 = d i

T 3j = т 32’      ;ф“= 0    ; U ⁽¹> = < U“|     ;

J J Ixз = h                 lxз = h                       lxз = h т3;*= т37| ,;фю = 0| „;-?"> = u°'| „;

^{J J} I x з = d 2                 l x з = d 2                       l x 3 = d 2

t3»= t«'|    ;U'3> = <7-4>| x3 =0                     lx3 =0

где d ₁, d ₂ и h – толщины верхнего, нижнего слоя металла и пьезоэлектрического слоя соответственно. В настоящей работе рассмотрен случай, когда d 1 = d 2 , т. е. толщины верхнего и нижнего слоев металла равны.

Подставляя в граничные условия уравнения упругой волны в виде линейных комбинаций парциальных волн

U, = E Cnm>a(n>exp [i (k1 x1 + k3(n>x3 - ®t)] , n

Ф = E C 4 m > а д > exp [ i ( k 1 x 1 + k ₃ ⁽ n > x ₃ - ю t ) ] , n

где верхний индекс n соответствует числу парциальных волн в соответствующем кристаллическом слое, получим систему уравнений – граничных условий. Равенство нулю определителя матрицы граничных условий (2), размерность которой в данном случае равна 24×24, позволяет определить характеристики упругой волны.

Вариации граничных условий (2) определяют все типы упругих волн, распространяющихся в слоистой структуре. Для рассматриваемых слоистых структур Me/ZnO/Me/алмаз и Me/AlN/Me/алмаз система уравнений граничных условий (2) разделяется на две независимые части: систему уравнений 16 x 16 для рэлеевских мод и систему уравнений 8 x 8 для SH -мод упругой волны. При использовании в слоистой структуре изотропных металлов, пьезоэлектрика группы симметрии 6 мм и диэлектрической подложки из кубического кристалла система уравнений для мод упругой волны Лява запишется в виде

С®k3nW2n) exp [ik3n)d 1 ] = 0,

С1 С44k3n) a2n) exp [ik3n) h]

• -    СП2) C44)k3m)a2m) exp [ik3m)h] = 0, сП2) C42) k3(nЦп) exp [ik3(n) d2 ] -

• -    СП3) C44) k3m)a2m) exp [ik3(m)d2 ] = 0,            (4)

C ^W™ ) exp [ ik 3m ) h J - C ^' a V') exp [ ik ₃ ^{( n} ) h J = 0, C,4 ,³⁾a 2 ^m ) exp [ ik ₃ ^{( m} ) d ₂ ] - C p V₂ ⁿ ) exp [ ik ₃ ^{( n} ) d ₂ ] = 0,

СП3) C44) k3n)a2n) - СП4) C44) k3n) a2n) = 0,

Cm3)a2m) - сП4)а2п) = 0, где цифровые верхние индексы 1–4 обозначают слои и подложку соответственно, по аналогии с уравнением (2); k3 – волновой вектор.

Анализ влияния массовой нагрузки в слоистой структуре. Массовая чувствительность S многослойного резонатора определяется из условия энергетического баланса как частотное изменение, т. е. сдвиг относительной частоты резонатора, нормализованный к поверхностной массовой плотности [13]:

S ⁼ W I/ f p ^ ) ⁼ f~ V^ f p ^ ) ,        (5)

I f ) J/         I v )!

где v , f – фазовая скорость и частота упругой волны. Однако недостатком данного подхода является то, что при больших значениях частоты f сглаживаются изменения фазовой скорости при увеличении толщины металлического слоя. Поэтому в настоящей работе для определения массовой чувствительности упругой волны использовалась следующая формула:

S v

A v

v

vmt - v vmt

где v mt – фазовая скорость упругой волны при нанесении тонкого металлического слоя, не изменяющего механических граничных условий. Отметим, что данное условие, как показал компьютерный эксперимент, выполняется при толщине слоя менее 1 нм. Также условие (6) нивелирует влияние пьезоэффекта, и, следовательно, параметр S v не будет зависеть от типа пьезоэлектрического слоя.

Схематическое изображение исследуемых слоистых структур представлено на рис. 1, а. Дисперсионные зависимости фазовых скоростей фундаментальной и первой моды волны Лява от значения параметра hxf (толщина пьезоэлектрика x частота) для слоистой структуры вида Me/ZnO/Me/алмаз с ориентацией [100] (001) слоя и подложки представлены на рис. 1, б, аналогичные зависимости для слоистой структуры вида Me/AlN/Me/алмаз с ориентацией [100] (001) слоя и подложки представлены на рис. 1, в. В качестве слоя металла (Me) использовались Al, Mo, Pt, обладающие различными значениями акустического импеданса Z = ρv. Выбор различных металлов позволяет также выяснить, как высокий/низкий акустический импеданс слоя влияет на изменение фазовой скорости упругой волны. Акустические импедансы используемых слоев соотносятся как ZAl < ZAlN < ZZnO < Zалмаз < ZMo < ZPt. Значения материальных констант используемых материалов для алюминия и молибдена взяты в [9], ZnO – в [14], AlN – в [15], алмаза – в [16], поликристалличе-ской платины – в [17].

Диапазон изменения фазовых скоростей SH -мод упругой волны в структуре Me/ZnO/Me/алмаз находится в пределах от значения фазовой скорости сдвиговой волны алмаза ( v = 12828,2 м/с) до фазовой скорости поперечно-поляризованной объемной сдвиговой волны в ZnO ( v = 4176,2 м/с).

В структуре Me/AlN/Me/алмаз фазовые скорости SH -мод упругой волны изменяются также от значения фазовой скорости сдвиговой волны алмаза до фазовой скорости медленной поперечно-поляризованной объемной сдвиговой волны в AlN ( v = 5808,8 м/с).

Расчет изменения мод фазовых скоростей упругой волны был произведен при относительных отношениях толщин металлических слоев к толщине пьезоэлектрика d / h = 0,005; 0,01; 0,05; 0,1. Сплошной линией на рис.1, б , в обозначены фазовые скорости мод упругой волны Лява ( SH -моды) при металлизации пьезоэлектрического слоя двумя бесконечно тонкими слоями металла, не нарушающими механических граничных условий. Штриховыми линиями на рис. 1, б , в обозначены фазовые скорости упругой волны при относительном отношении толщины слоя металла к слою пьезоэлектрика d / h = 0,1. В абсолютных значениях представленные значения фазовых скоростей можно представить при толщинах слоев пьезоэлектрика h = 10 мкм и металла d = 1 мкм при изменении частоты от 1 МГц до 1 ГГц.

Использование слоев металла в слоистой структуре может существенно повлиять на перераспределение упругой энергии волны вследствие акустических свойств самих слоев или сложной интерференции между модами упругой волны, падающими и отраженными от границы раздела слоев. Например, в структурах Pt/ZnO/Pt/алмаз и Pt/AlN/Pt/алмаз при увеличении значений h x f фазовые скорости SH -мод (волны Лява) упругой волны стремятся к значению фазовой скорости объемной сдвиговой волны в Pt. Аналогичная ситуация проявляется и при использовании в многослойной структуре других металлов. При этом отмечается, что в структуре Me/AlN/Me/алмаз скорости SH -мод упругой волны при одинаковом типе металла и значении параметра h x f уменьшаются более значительно, чем в структуре Me/ZnO/Me/алмаз.

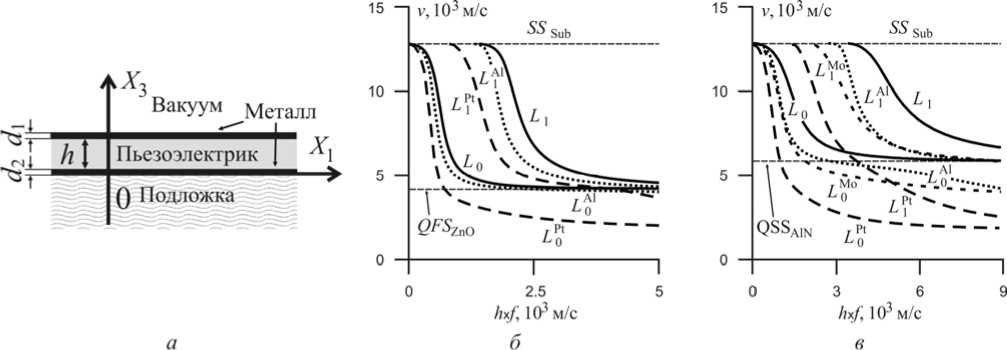
Рис. 1. Дисперсионные зависимости фазовых скоростей от произведения h х f для слоистой структуры Me/пьезоэлектрик/Me/алмаз: а – схема слоистой структуры; б – моды SH -волны L ₀ и L ₁ в структуре Me/ZnO/Me/алмаз; в – моды SH -волны L ₀ и L ₁ в структуре Me/AlN/Me/алмаз; сплошные линии – скорости мод при бесконечно тонких слоях металла, штриховые линии – скорости при толщине слоев металла d / h = 0,1

Fig. 1. Dispersive dependence of phase velocities on the product h x f for the layered structure Me/Piezoelectric /Me/diamond: a – the scheme of the layered structure; b – SH-wave mode L₀ and L₁ in the structure Me/ZnO/Me/diamond; c – SH-wave mode L₀ and L₁ in the structure Me/ AlN/Me/diamond. Solid lines – mode velocities for infinitely thin metal layers, dash lines – mode velocities for metal layers thickness d / h = 0,1

На рис. 2 представлены графики относительного изменения фазовых скоростей S v (6) фундаментальной моды L 0 и первой моды L 1 волны Лява в зависимости от типа металлического слоя, отношения d / h и параметра h х f в структуре Me/ZnO/Me/алмаз. Максимальные значения параметра S v моды L 0 достигаются при значении h х f = 600-700 м/c при использовании всех типов металлических слоев и отношении d/h = 0,1 (рис. 2, а – в ). При использовании слоев Al и Mo значения параметра S_v = 0,24 и S_v = 0,26 соответственно, но для структуры Pt/ZnO/Pt/алмаз параметр S v = 0,49. Необходимо отметить, что увеличение толщины металлического слоя приводит к смещению частоты сигнала при достижении максимальных значений параметра S v . Существенный рост значений параметра S v особенно проявляется с ростом значений h х f при отношении d/h > 0,05. Данное увеличение значений S v особенно существенно для металлов с высоким значением акустического импеданса для фундаментальной моды L 0 упругой волны. Однако численные значения S_v в зависимости от типа металла существенно отличаются, например, в структуре Al/ZnO/Al/алмаз S v = 0,11 при h х f = 8500 м/c, а в структуре Pt/ZnO/Pt/ алмаз S v = 0,56 при аналогичном значении h х f .

Максимальные значения параметра S_v для моды L ₁ упругой волны Лява достигаются при h х f = 2100 м/c, где выполняется условие h = λ/4, т. е. толщина пьезоэлектрического слоя равна четверти длины упругой волны (рис. 2, г – е ). Однако в отличие от фундаментальной моды L 0 для первой моды L 1 волны Лява величины параметра S v с ростом значений h х f уменьшаются при использовании металлических слоев Al или Mo, но для структуры Pt/ZnO/Pt/алмаз при отношении d / h = 0,1 происходит резкий рост значений параметра S v (рис. 2, е ).

На рис. 3 представлены графики относительного изменения фазовых скоростей S v фундаментальной и первой моды волны Лява в зависимости от типа металлического слоя, отношения d / h и параметра h х f в структуре Me/AlN/Me/алмаз.

Максимальные значения параметра S v моды L 0 достигаются при значениях h х f = 1300-1400 м/c при использовании всех типов металлических слоев и отношении d/h = 0,1 (рис. 3, а – в ). При использовании слоев Al и Mo значения параметра S v = 0,27 и S v = 0,31 соответственно, а для структуры Pt/AlN/Pt/алмаз параметр S v = 0,55. Значения параметра S v на 12–13 % превышают аналогичные значения для структуры Me/ZnO/Me/алмаз, при этом увеличение толщины металлического слоя также приводит к смещению частоты сигнала при достижении максимальных значений параметра S_v . При этом в отличие от предыдущей структуры для фундаментальной моды L 0 упругой волны отмечено существенное увеличение значений параметра S v для всех типов металлов при отношении d/h > 0,05. Величина параметра S_v при больших значениях h х f может быть сравнима или даже превышать значения в локальном максимуме при h х f = 1300-1400 м/c. Например, в структуре Al/AlN/Al/алмаз S v = 0,26 при h х f = 8500 м/c, а в структуре Pt/AlN/Pt/алмаз S v = 0,73 при аналогичном значении h х f

Максимальные значения параметра S v для моды L 1 упругой волны Лява достигаются при h х f = 4300 м/c, где выполняется условие h = λ/4, т. е. толщина пьезоэлектрического слоя равна четверти длины упругой волны (рис. 3, г – е ). В целом характер изменений параметра S_v аналогичен изменениям S_v в предыдущей слоистой структуре.

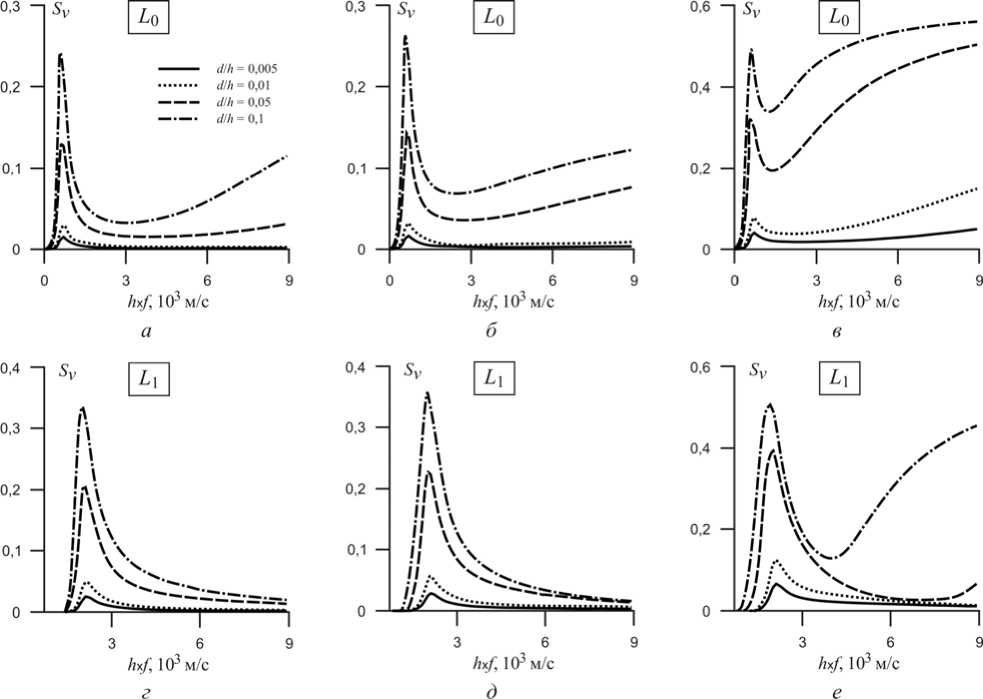
Рис. 2. Дисперсионные зависимости изменения фазовых скоростей моды L 0 и L 1 от произведения h х f для слоистой структуры Me/ZnO/Me/алмаз: а , г – алюминий; б , д – молибден; в , е – платина; отношение толщин металла и пьезоэлектрика d / h : 0,005; 0,01; 0,05; 0,1

Fig. 2. Dispersive dependence of the change of phase velocities of the mode L 0 and L 1 on the product of h х f for the layered structure Me/ZnO/Me/diamond: a ( а ), d ( г ) – aluninium; b ( б ), e ( д ) – molybdenum; c ( в ), f ( е ) – platinic. Ratio of the metal layers and piezoelectric d / h : 0,005; 0,01; 0,05; 0,1

При создании устройств акустоэлектроники желательно представлять характер зависимости характеристик упругой волны от свойств дополнительных слоев. На рис. 4 представлены зависимости параметра S v от величины значения d / h для фундаментальных и первых мод упругой волны в обеих слоистых структурах.

В случае рассмотрения структуры Me/ZnO/Me/алмаз линейная зависимость наблюдается только при использовании слоев Al (рис. 4, а ). Например, для фундаментальной моды L 0 волны Лява при h х f = 700 м/с и первой моды L 1 при h х f = 3400 м/с зависимость S_v от величины значения d / h аппроксимируется выражением S v = = 2,2∙ d / h и S_v = 0,94∙ d / h соответственно. Однако уже для структуры Mo/ZnO/Mo/алмаз наблюдается квадратичная зависимость S_v = –9,3∙( d / h )² + 3,2∙ d / h для фундаментальной моды L 0 и S v = –6,4∙( d / h )² + 1,6∙ d / h для моды L 1 . При использовании слоев платины присутствует явно выраженная квадратичная зависимость S v = –30,6∙( d / h )² + 7,5∙ d / h для фундаментальной моды L 0 и S v = –17,4∙( d / h )² + 3,1∙ d / h для моды L 1 . При этом наблюдаются максимальные величины параметра S v для фундаментальной моды волны Лява при отношении d/h = 0,1. В целом в рассмотренной структуре мода L 0 обладает большей чувствительностью при всех типах металлов, чем первая мода волны Лява.

В случае рассмотрения упругих волн Лява в структуре Me/AlN/Me/алмаз линейная зависимость уже не наблюдается (рис. 4, б ). Например, для фундаментальной моды L ₀ волны Лява при h х f = 1300 м/с и первой моды L 1 при h х f = 4400 м/с зависимость S_v от величины значения d / h аппроксимируется выражением S v = = –9,6∙( d / h )² +3,7∙ d / h и S v = –17,5∙( d / h )² + 5,4∙ d / h соответственно. При использовании слоев платины присутствует явно выраженная квадратичная зависимость: S v = –35∙( d / h )² + 9∙ d / h для фундаментальной моды L 0 и S v = –48,6∙( d / h )²+10,7∙ d / h для моды L 1 . При этом максимальные величины параметра S v наблюдаются для первой моды волны Лява при отношении d/h = 0,1. В отличие от предыдущей структуры, мода L 1 обладает большей чувствительностью при всех типах металлов, чем фундаментальная мода волны Лява.

Необходимо отметить, что подобные зависимости параметра S v прослеживаются на всем рассмотренном частотном интервале. Таким образом, в многослойных структурах Me/ZnO/Me/алмаз и Me/AlN/Me/алмаз чувствительность S v находится в прямой зависимости от значения акустического импеданса металлического слоя.

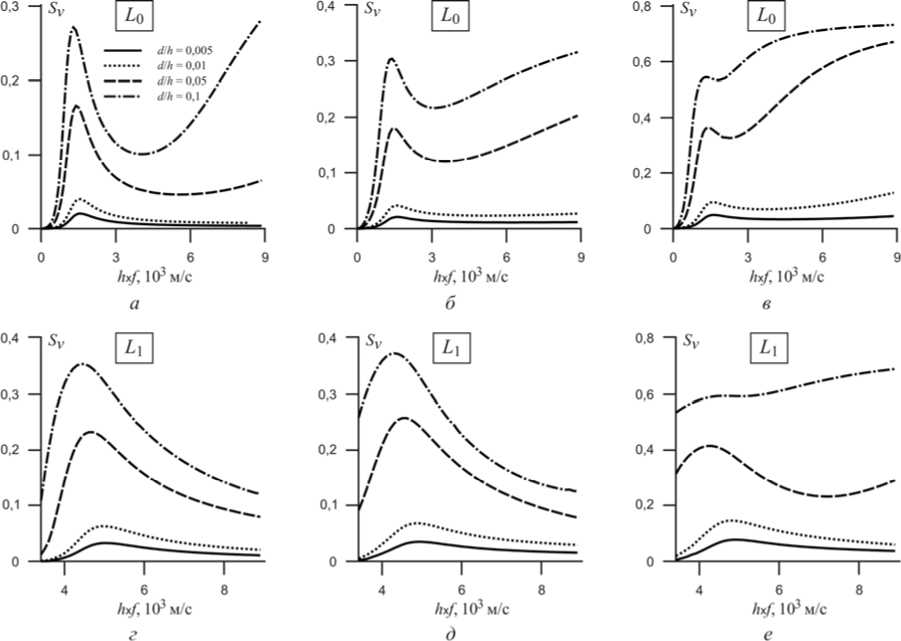
Рис. 3. Дисперсионные зависимости изменения фазовых скоростей моды L 0 и L 1 от произведения h x f для слоистой структуры Me/AlN/Me/алмаз: а , г - алюминий; б , д - молибден; в , е - платина; отношение толщин металла и пьезоэлектрика d / h : 0,005; 0,01; 0,05; 0,1

Fig. 3. Dispersive dependence of the change of phase velocities of the mode L 0 and L 1 on the product of h x f for the layered structure Me/AlN/Me/diamond: a ( а ), d ( г ) - aluninium; b ( б), e ( д ) -molybdenum; c ( в ), f ( е ) – platinic. Ratio of the metal layers and piezoelectric d / h : 0,005; 0,01; 0,05; 0,1

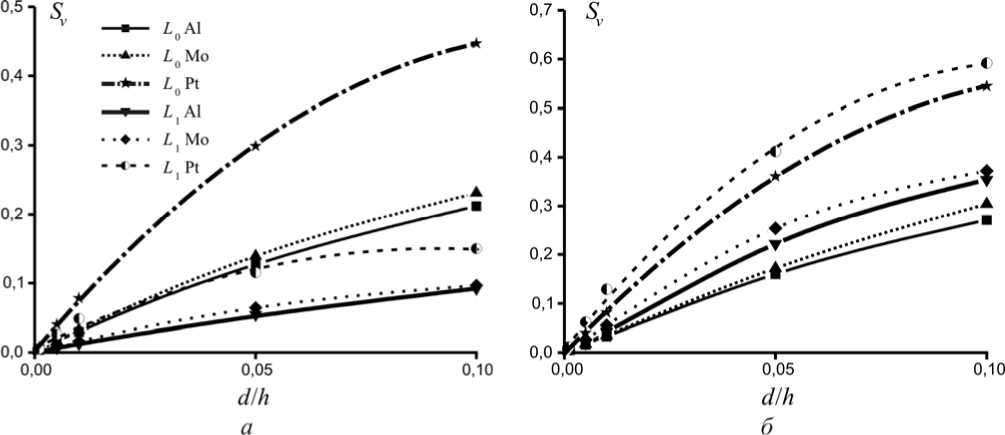
Рис. 4. Графики зависимости S_v отношения от толщины металла: a – структура Me/ZnO/Me/алмаз, мода L ₀ при h x f = 700 м/с и мода L 1 при h x f = 3400 м/с; б - структура Me/AlN/Me/алмаз, мода L ₀ при h x f = 1300 м/с и мода L 1 при h x f = 4400 м/с

Fig. 4. Dependency Graphs of the dependency of S v ratio on the metal thickness: a – the structure Me/ZnO/Me/diamond, mode L ₀ of h x f = 700 м/с and mode L 1 of h x f = 3400 м/с; b - the structure Me/ AlN /Me/diamond, mode L ₀ of h x f = 1300 м/с and mode L 1 of h x f = 4400 м/с

При рассмотрении условий распространения упругой волны в пьезоэлектрической структуре типа Me/пьезоэлектрик/Me/алмаз возникает следующий вопрос: каким образом верхний или нижний металлический слой влияет на изменение фазовой скорости волны? Установлено, что для геометрически несимметричной многослойной структуры, когда толщины металлических слоев и/или типы материалов варьируются, значения параметра S v будут отличаться.

На рис. 5 представлены дисперсионные зависимости фундаментальной моды L 0 волны Лява от величины параметра h х f в структурах Me/ZnO/алмаз и ZnO/Me/алмаз. В структуре Me/ZnO/алмаз характер изменения параметра S_v при использовании различных металлов качественно подобен поведению параметра S v в структуре Me/ZnO/Me/алмаз. Однако отмечено, что если в структурах Al/ZnO/Al/алмаз и Mo/ZnO/Mo/алмаз величины параметра S v сравнимы (см. рис . 2, а , б ), то для структур Al/ZnO/алмаз и Mo/ZnO/алмаз значения параметра S v существенно отличаются (рис. 5, а , б ). В частности, при использовании Al при значении h х f = 700 м/c и d / h = 0,1 значение параметра S v = 0,075, а при использовании Mo величина S v = 0,21. Для структур Pt/ZnO/Pt/алмаз и Pt/ZnO/алмаз характер поведения и значения параметра S_v практически не меняются (рис. 2, в , рис. 5, в ).

В структурах ZnO/Me/алмаз характер поведения дисперсии параметра S v моды L 0 меняется: высокие значения чувствительности сменяются низкими, и наоборот. Например, при использовании слоя Al при значении h х f = 700 м/c и d/h = 0,1 параметр S v = 0,18, для Mo S v = 0,06, и для Pt S v = 0,12.

На рис. 6 представлены дисперсионные зависимости фундаментальной моды L ₀ волны Лява в структурах Me/AlN/алмаз и AlN/Me/алмаз . В структуре Me/AlN/алмаз характер изменения параметра S v при использовании различных металлов качественно подобен поведению параметра S v в структуре Me/AlN/Me/алмаз. Аналогично рассмотренному предыдущему случаю с несимметричной металлизацией структур ZnO/алмаз в структурах Al/AlN/Al/алмаз и Mo/AlN/Mo/алмаз величины параметра S v сравнимы (см. рис. 3, а , б ), а для структур Al/AlN/алмаз и Mo/AlN/алмаз значения параметра S v существенно отличаются (см. рис. 6, а , б ). В частности, при использовании Al при значении h х f = 1600 м/с и d / h = 0,1 значение параметра S_v = 0,09, а при использовании Mo величина S v = 0,26. Для структур Pt/AlN/Pt/алмаз и Pt/AlN/алмаз характер поведения и значения параметра S v практически не меняются (см. рис. 3, в , рис. 6, в ).

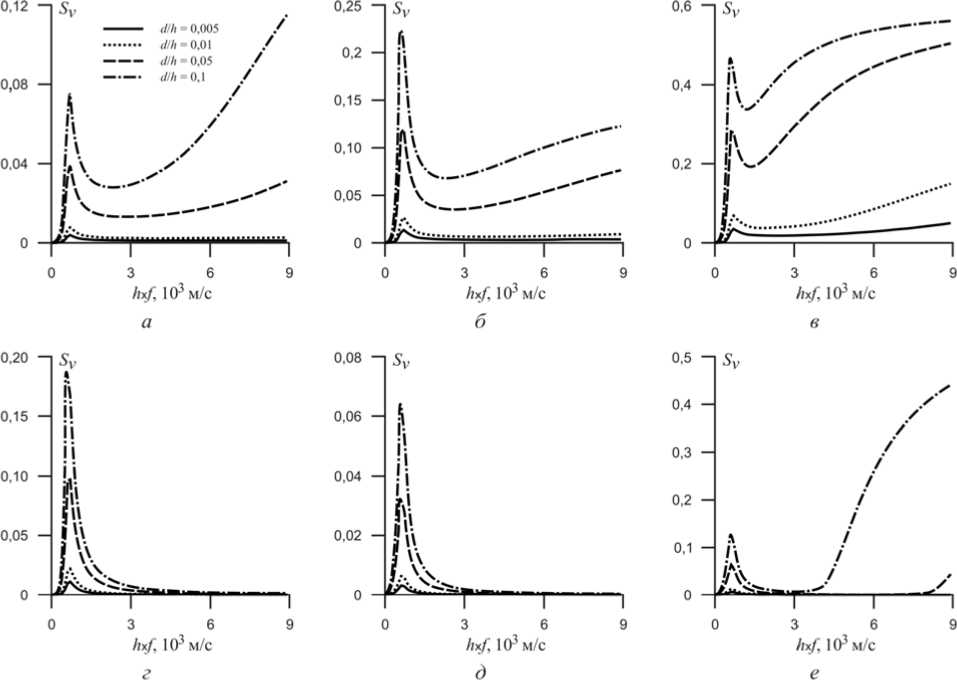
Рис. 5. Дисперсионные зависимости изменения фазовых скоростей моды L ₀ от произведения h х f для слоистой структуры Me/ZnO/алмаз ( а – в ) и ZnO/Me/алмаз ( г – е ): а , г – алюминий, б , д – молибден, в , е – платина; отношение толщин металла и пьезоэлектрика d / h : 0,005; 0,01; 0,05; 0,1

• Fig. 5.    Dispersive dependence of the change of phase velocities of the mode L ₀ on the product of h х f for the layered structure Me/ ZnO /Me/diamond ( а – в ) and ZnO/Me/diamond ( г – е ): a ( а ), d ( г ) – aluninium; b ( б ), e ( д ) – molybdenum; c ( в ), f ( е ) – platinic. Ratio of the metal layers and piezoelectric d / h : 0,005; 0,01; 0,05; 0,1

  

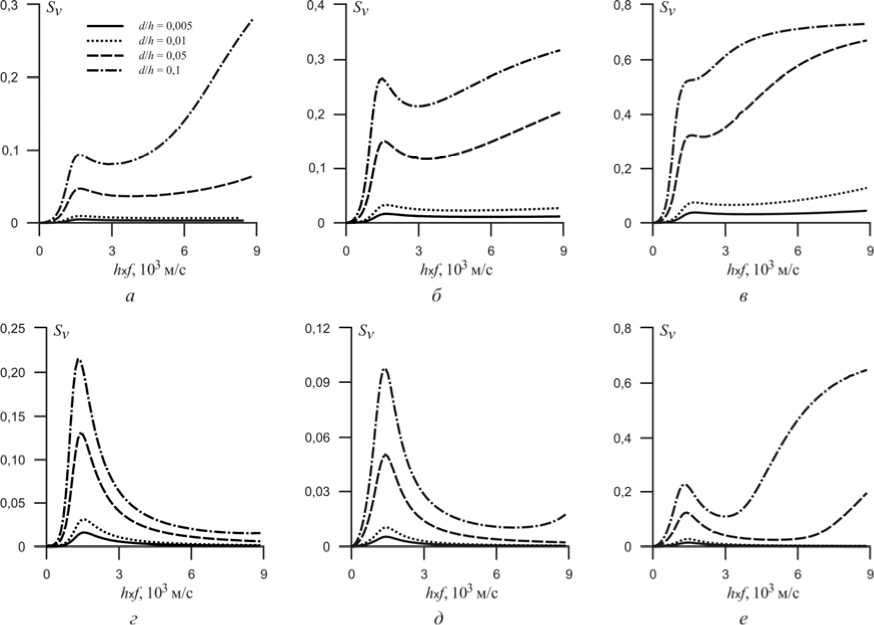
  Рис. 6. Дисперсионные зависимости изменения фазовых скоростей моды L 0 от произведения h х f для слоистой структуры Me/AlN/алмаз ( а – в ) и AlN/Me/алмаз ( г – е ): а , г – алюминий; б , д – молибден;

  в , е – платина; отношение толщин металла и пьезоэлектрика d / h : 0,005; 0,01; 0,05; 0,1

  
  

• Fig. 6.    Dispersive dependence of the change of phase velocities of the mode L 0 on the product of h х f for the layered structure Me/ AlN /Me/diamond ( а – в ) and AlN /Me/diamond ( г – е ): a ( а) , d ( г ) – aluninium; b ( б ), e ( д ) – molybdenum; c ( в ), f ( е ) – platinic. Ratio of the metal layers and piezoelectric d / h : 0,005; 0,01; 0,05; 0,1

В структурах AlN/Me/алмаз характер поведения дисперсии параметра S v моды L 0 также меняется: высокие значения чувствительности сменяются низкими, и наоборот. Например, при использовании слоя Al при значении h х f = 1300 м/c и dIh = 0,1 параметр S_v = 0,22, для Mo S_v = 0,097, и для Pt S_v = 0,23.

Таким образом, в обоих типах структур с несимметричной металлизацией при высоких значениях акустического импеданса металлического слоя максимальные значения чувствительности достигаются при наличии верхнего металлического слоя, т. е. в структуре Me/ZnO/алмаз и Me/AlN/алмаз, а при низких величинах акустического импеданса – в структурах при наличии промежуточного металлического слоя (ZnO/Me/алмаз и AlN/Me/алмаз).

Заключение. Влияние массовой нагрузки в виде двух металлических слоев (моделирующих верхний и нижний электрод) на изменение фазовой скорости Δv/v дисперсионных мод упругой волны в пьезоэлектрических слоистых структурах Me/ZnO/Me/алмаз и Me/AlN/Me/алмаз в зависимости от частоты и отношения d/h находится в прямой зависимости от значения акустического импеданса металлического слоя. Отмечено, что максимальные значения изменения фазовых скоростей мод упругой волны Δv/v достигаются при конфигурации слоистой системы Pt/AlN/Pt/алмаз. Кроме того, структуры Me/AlN/Me/алмаз обладают большим значениями чувствительности Sv, чем струк- туры Me/ZnO/Me/алмаз. Обнаружено, что максимальные значения величин Δv/v достигаются, если толщина металлического слоя кратна четверти длины упругой волны. Необходимо отметить, что при низких значениях акустического импеданса металлического слоя более существенные изменения величин Δv/v происходят вследствие изменения толщины нижнего электрода. Однако если акустический импеданс металлического слоя сравним с акустическим импедансом подложки, то в данном случае увеличение значений величин Δv/v в большей степени обусловлено толщиной верхнего металлического слоя.

Полученные результаты могут быть полезными при разработке управляемых акустоэлектронных устройств на волнах Рэлея и Лява.