Введение. Выполняя защитную или иные функции, тонкие покрытия изменяют механические характеристики изделий. Кроме того, покрытия могут подвергаться постоянно растущей нагрузке. Таким образом, представляется интересной разработка методов оценки напряжённого состояния в упругих телах, ослабленных технологическими и эксплуатационными дефектами и усиленных тонкими покрытиями и накладками. Решение этой актуальной задачи отвечает потребностям современного производства.

Первые исследования по изучению тонких накладок, изгибной жёсткостью которых можно пренебречь, приведены в работах Э. Мелана [1], Э. Рейсснера [2], В.-Т. Койтера [3], а также отечественных учёных [4]. В работе В. М. Александрова и С. М. Мхитаряна [5] собраны результаты многих исследований по контактным задачам для тел с тонкими покрытиями и прослойками. В [6] решена контактная задача о передаче нагрузки от периодической системы стрингеров к полосе, ослабленной трещиной.

Математическая постановка задачи. Рассмотрим статическую задачу теории упругости для полуплоскости -да <  x <  да , у <  0, ослабленной внутренней прямолинейной трещиной длиной 2 а , перпендикулярной её границе. Центр трещины расположен на расстоянии h от поверхности. К берегам трещины приложены нормальные усилия интенсивности p ( у ) , поддерживающие её в раскрытом состоянии.

При y = 0 действует граничное условие, моделирующее влияние накладки [5]:

AGhu ^( l - V 1 ) т _Х у - 2V i h i O y , о„ = 0.

Здесь и далее G_i , ν _i — модуль сдвига и коэффициент Пуассона соответственно накладки ( i = 1 ) и полуплоскости ( i = 2 ); h ₁ — толщина накладки; τ _xy , σ _y — компоненты тензора напряжений в полуплоскости; производные берутся по переменной x .

Задача о равновесии полосы -* <  х <  * , 0 <  y < - h ₂ , усиленной покрытием на границе y = 0 , формулируется аналогично задаче для полуплоскости. При этом одновременно с (1) на нижней грани ( y = - h ₂) действует одно из следующих условий: задача A — гладкий контакт т xy = 0, v = 0;

задача B — жёсткая заделка и = 0, v = 0;

задача C — свободная поверхность a _У = 0, т xy = 0.

Как уже отмечалось, граничное условие (1) сформулировано на основе вывода базовых уравнений для тонких упругих покрытий (прослоек) в плоском случае путём асимптотического анализа точного решения задачи теории упругости для полосы [5]. В указанной работе получены определяющие соотношения тонких упругих покрытий, однако их эффективности не исследовалась.

В [7] описан цикл вычислительных экспериментов в конечноэлементном пакете FlexPDE. Исследование показало, что при замене накладки граничным условием погрешность моделирования растёт с увеличением жёсткости и толщины накладки. При относительной толщине накладки h 1 / h ₂ <  0,02 и в широком диапазоне изменения физических параметров модели погрешность определения полей напряжений не превышает 5 %.

Решение. Введём следующие обозначения для разрывов функций перемещений при x =0 :

u ⁽ x , У )С= X ⁽ У ) ,

/        \ +0

d v ( х , y )

д х

- 0

-V ( У ) .

Касательные усилия на берегах трещины отсутствуют. Учитывая это, можно установить связь между разрывами функций (2), которые подлежат в дальнейшем определению:

W ( У ) = - X ‘ ( У ) .                                               (3)

Применим интегральное преобразование Фурье по x к уравнениям равновесия в перемещениях для случая плоской деформации в виде F f ( х , y ) ] = J f ( х , y ) e ^a x dx .

-*

Приняв во внимание соотношения (2), (3) и то, что при х > ■ * все компоненты вектора перемещений и их производных убывают, имеем:

* д и ( х , у ) .

j — ---- -e ^{a x}dx = X ( y ) - iaU ( y ) ,

-* д х

* ^д u ^{( Х} , ^У ) e ^{a x} dx = -i a X ( у ) - a ² U ( у ) , -*    д х ²

*дv(х,y) .,

[ — ----- e ^{a x}dx = - i a V ( y ) ,

J    дх

-*

• * д2v^x, y)                  , ., , .

J — ( х^г- ) - e ^{a x}dx = ^ф ( у ) - a ² V ( У ) .

В результате получим неоднородную систему обыкновенных дифференциальных уравнений в трансформантах Фурье по x :

( 1 - 2v ) U "( y ) - 2 ( 1 - v ) a² U ( y ) - i a V ' ( y ) = 2 ( 1 - v ) i a X ( y ) , 2 ( 1 - v ) V "( y ) - ( 1 - 2v ) a² V ( y ) - i a U ' ( y ) = - 2v X ' ( y ) .

Применим к (4) интегральное преобразование Фурье по у в виде F ff (у)] = J f (y)ei3ydy . По--to лучим систему линейных алгебраических уравнений относительно трансформант U, V :

'((1 - 2v) в2 + 2 (1 - v) а2) U + ав V = -2 (1 - v) iаX, ав U + ((1 - 2v) а2 + 2 (1 - v) в2 V = -2v/₽X.

Её решение:

1 ^а ( ^а 2 ⁽ v - 1 ^{) + в} 2 ⁽ v - ^{2 )})

U =--;--------:------- X ,

( v - 1 ) ( а ² + в ² ) ²

i p ( ^а 2 ^{( v} - 1 ^{) + в2v} ) V =---------------- — X .

( v - 1 ) ( а² + в² )

Произведём обратное преобразование Фурье (5), (6) по у в виде F "1 f F ] = — J Fe" i P ^ydy . После

-to ряда непосредственных преобразований получим общее решение системы (4) в виде:

f U = U 0 + U 1 ,

V = V , + V 1 .

U0 = (C1 + C2 |а| y) ey| а| + C + C4 |а| y) e "y| а|, v=i sgn (а) (C+(i а y -к) C2) eyi а| - (C3+(i а y+к) C4) e ■y| а|).

U 1 = /Т 1, - h J⁺ * X (n) e - ' ^y ' (³ - 2v - l°lln - y |) d n,

⁽        ) - h - *

V = - 4(v1-1) hJX(n) e-а'П-y| sgn(n - y)(2v - ■* - у|)dn, где к = 3 - 4v, C1 - C4 — произвольные постоянные, подлежащие определению из граничных условий.

Рассмотрим первоначально предельный случай h₂ > ■/ , соответствующий задаче для полуплоскости. Учитывая затухание решений при y ^ -to в этом случае, в (7) следует положить

C ₃ = C ₄ = 0 . Постоянные C ₁ и C ₂ определяются из условий (1), представленных в терминах трансформант:

4 G . h . а^/ U + ( 1 - v 1 ) G (U' - / а V ) = 0,

\1 - v ) V ‘- / аv U = 0;

C =—;---- i sgn ^ ^ THf + ^x ( n ) f| а|^n G ( 4v - 3 )( v - 1 ) - 4 Gh ( v - 1 )( 2v - 3 )) + ¹     4 ( v - 1 ) ( 4 G 1 h 1 ( v - 1 ) ^| + G ( У 1 - 1 ) ) - h - * ^{U7LII(I ( Л 1}     )      ¹¹                 ) )

+ G ( 6v - 5 ) ( v 1 - 1 ) + 4 G ₁ h ₁а²n ( v - 1 ) ] e*¹ d n;

C = w i , -----;-----h + *X (n)f(2n G (v_x - 1) - 4 Gh (v - 1)) + 3 G (v, - 1) 1 e^d n.

• ² 4 ( v - 1 ) ( 4 G 1 h 1 ( v - 1 ) |а| + G ( v 1 - 1 ) ) - h - _a                   ^{1                                    1}    ^J ¹

Таким образом, составим интегральное уравнение задачи на основе принципа суперпозиции, удовлетворив условию a x - — p ( y ) на берегах трещины при x = 0:

x du dv

(1 — v)— + v— = v ’dx dy

—

1 — 2v

2G ^P( y ) .

В результате непосредственных, но довольно громоздких преобразований задача сводится к решению гиперсингулярного интегрального уравнения:

—I

—

- h + a

J X (n)

h — a

+ K *(п, y ) d n -

—

2п ( 1 — v )

G

p ⁽ y ) ,

K ’ (n, y ) =

—

^k 1 ^k 2 ( n ⁺ y ) 3

_{(                                             —} k 2 ( n + y )

12 ( n k 2 — 2 k 1 )( k 2 y — 2 k 1 ) e ^{k 1} E 4

к

⁽ — Win))

k к 1      7

к

^{+ k} 1 ( ^k 2 ( n ⁺ y ) ^{— 16 k} 1 ) .

Здесь Ek (5)- je^dt — интегральная экспонента [8], k =4Gh (v — 1), k2 = G(vt — 1). Произве-1 tk дём интегрирование по частям в (10), c учётом очевидного свойства функции X (y): X (—h — a) = X (—h + a) = 0 . В результате получим сингулярное интегральное уравнение первого рода с ядром Коши относительно функции X'(y).

X 12 ( k i — nk )( 2 k к

— h + a

J X'(n)

— h — a

L n — y

+ K ( n, y ) d n -

—

2n ( 1 — v) , x G    p ( y ) .

K ( n, y ) --- ¹---- 3

k 2 ( n + y ) 3

_— k 2 ( n + y )      (

^— k 2 y ) e    k¹ E 4

—

к

k ^f y ^n) ] k ¹     7

X

A

— 8 k 1 ² + 4n k 1 k ₂ + k ₂ ² ( n ² —

Cингулярная часть (11) соответствует задаче о прямолинейной трещине в неограниченной упругой плоскости [9]. Регулярная часть (12) отвечает за влияние различных физических и геометрических параметров.

Положим, 0 - k 1 / k ₂. Выделим слагаемое регулярной компоненты ядра (12), соответствующее задаче о поперечной трещине в полуплоскости без накладки [10]:

(

( n + y)

х y ² — n ² + 4n y

K (n, ¥)-   / x3   +(n + y)

4 0 ( 20 — n ) — 3 ( 0 — n )( 20 — y ) e" ⁰ E 4

—

7 7

(n + y )3

.

Нетрудно заметить, что предельный переход в (13) при 0 w 0 оставляет в регулярной части ядра отличным от нуля только первое слагаемое, отвечающее за влияние границы полуплоскости.

Метод малого параметра. Определим следующие переменные и функции в выражении (11):

f 0 ^{м -} a , g'( Z ) - X ' ( a Z - h ) , "  L ( Z, z ) - K ( a Z — h , az — h ) ,

f (z)-

² ( v — 1 )

J g'( z )

— 1

G

_ Z — z

p ( az — h ) - const;

+ aL ( Z, z ) d Z - n f ( z ) .

Введём безразмерный параметр A - a / h , (A<1), характеризующий относительное расстояние между трещиной и границей тела:

A ( A ( - Z ( ZA + 2 ) + A z ² + z ( 4ZA - 6 ) ) + 4 )

^{L ( Z}, z ) =                ( A ( Z + z ) - 2 ) 3                +

+

Г                                                2 - A ( Z + z )

4 ЗА ^{- 2} ( Ар - ZA + 1 )( A z - 2Ар - 1 ) e ‘ E ₄

I

Г 2 - ( z + Z ) А )

Ар

V м 7

( Z + z - 2A ^{- 1} ) ³

)

+ р ( 2р - Z + А ^{- 1} )

.

Первоначально будем строить решение сингулярного интегрального уравнения (14), предполагая, что относительное расстояние между трещиной и границей тела достаточно велико: А « 1.

C этой целью представим регулярную часть ядра L ( Z, z ) в виде разложения по степеням параметра λ :

L ( Z, z ) = ^nj_i ( Z, z ) А i + O ( А ^{n + 1} ) ,

l ( Z, z ) -- 2,

4 ( Z, z ) = 4 ( P - ²Z ) -

1 3 ( Z, z ) - 4 ( - Z² + 2ZP - P 2 + z ² - 2Z z ) ,

• 1 4    ( Z, z ) = 116 ( - Z³ + 6Z²P - 12ZP² + 12р³ + 5 z ³ - 3Z z ² - 6p z ² - 9Z² z + 12Zp z ) ,

• 1 ₅    ( Z, z ) - ;32 ( Z⁴ + 4Z 3 P - 24Z 2 P 2 + 72ZP³ - 96р⁴ + 9 z ⁴ + 4Z z ³ - 20p z ³ - 18Z 2 z ² + + 12Zp z ² + 24р² z ² - 12Z³ z + 36Z²p z - 48ZP² z + 24р³ z ) .

Решение будем строить в виде асимптотического разложения по степеням этого параметра: g ( z ) y g '< z ) а i + о ( а ■ ^{+ 1} ) .

i - 1

Реализуя разложения (15) и (16) в уравнении (14) и сопоставляя выражения при соответствующих степенях λ, получаем цепочку последовательно разрешаемых интегральных уравнений относительно функций gi (z), i - 1,2, j^g;( z ) dz=nf (z), j [      g1(z)+k1 g 0(z)1 dZ - 0,

• - 1 L ^z z                     _

  
  

j ^[ 17- g n ( Z ) + У k „ - _ g ; ( Z ) 1 d Z - 0, n - 1,2, - ;

• - 1 L ^{Z -} z           m - 0             J

Запишем оператор обращения для первого из этих уравнений [11]:

J т^д'к z ) ^d z - ⁿ f ( z ) , - 1 ^ z <  1,

• - 1 '

  g ^{,( z} )

  
  

  nV1 - zz-

  
  

  J £-1 1 f ( z ) d z.

  - 1 ^{z - z}

  
  

Решая уравнения цепочки (17), найдём g „ , n = 1,2,... и представим решение в виде:

fz

g( z ) = z

^{1 +} 4^Л 2

V

—

( 2 z ( m — z ) + 1 )    + ( 24 ц + z ( 12( z — 2 ц )² + 5 ) )

8 z

128 z

—

—

( 24р² + 4 z ⁴ + 12m z 3 — 3 ( 16М² + 5 ) z ² + М ( 72М 2 + 5 ) z + 6 )

64 z

)

^Л 5 + О ( Л ‘ ) .

Анализ структуры (18) показывает, что наличие свободной границы усиливает концентрацию напряжений в окрестности края трещины, а покрытие снижает этот эффект. Причём первый из названных факторов имеет порядок λ ² , а второй — более высокий — λ ³ .

Метод коллокации. Построим решение интегрального уравнения (14) методом коллокации в виде линейной комбинации базисных функций, явно учитывающих особенность в окрестности края трещины:

m

g'( z )=^x,t„ ( z ).

V1 — z 2 n = 0

При этом

m g (Z ) = — x1 z БХ^ (Z), n =0     „ где Tn, Un — полиномы Чебышёва I и II рода соответственно, Xn — коэффициенты базисных функциях, m — количество узловых точек.

В качестве узловых точек принимаем корни полиномов Чебышёва:

п ( 2i — 1) /. 4

m ) .

,...,

z i = cos ₂ m   ' ⁽ i = 1,2

Для определения коэффициентов X_n необходимо составить и решить систему линейных алгебраических уравнений

[ a - a

a ₁ a

I a mi

a_{m 2}

2m a1 a

' 1 m )

a mm 7

[ X 1 ] X 2	=	z п ^ ( z ) п ^ ( z )
л„.		V п ^ ( z )

л

с коэффициентами a j = J T j ( Z )

— 1

- L z

^— z i

+ K (Z, z i ) d Z.

Зная g'( z ) , легко установить значение коэффициента интенсивности нормальных напряжений:

^ki =^— iim₀ [ ^e p^ ^{2п ( 1 — z} ) g '^{( z} ) ] .

z ^-1—0L

При выборе числа узлов коллокации следует учитывать значение параметра λ . C увеличением λ точность решения падает. При значениях λ = 0,95 для получения решения в рамках принятой модели c точностью не менее 99 % необходимо минимум 8 узлов коллокации.

В случае полосы в решениях (7), (8) необходимо удовлетворить условиям на нижней грани для каждой из задач A - C Повторив рассуждения (2)—(11), найдём C 1 A — 4 ^е и получим сингулярные интегральные уравнения относительно производной функции раскрытия трещины X A — е ( П ) ^:

— J

—

• h + a

J X A — c ( n ) h — a

“

-1 - ₊J R„ ( n, У ,о ) e-'

I У —to

d a d n =

—

2п ( 1 — v )

G p ( ⁽ у ) .

Подынтегральная функция в регулярной части ядра интегрального уравнения (19) имеет устранимую особенность при α = 0 :

4n - 9 + 2h aim RA(n, y,a) = - 9 + 2h 2, limRB (n,у,о) = -1,(21)

a—0

( h 2 + h 2 ( 8n — 29 ) + 6 h ₂ ² ( n ² + 2n У - 9 У ) + 12n ² h ₂ У + 6n 2 9 У )

lim R (n, y,a) = ----------------------Ц--------— ----------------- .(22)

a - о C ^{( 1,7}, )                                   h 3 ( 29 + h₂ )

Для выражений (20), (21), (22) справедливо: к = 3 - 4v, w 1 = 9|a| -1, w ₂ = 9|a| +1.

Полные выражения для подынтегральных функций R A - C ввиду их громоздкости здесь не приведены.

В результате асимптотического анализа было установлено, что при a > ■< подинтегральные функции R A - C ( n, y , a ) убывают как:

|a| e - ^{a|(n + y + 2 h} 2 ) , h ₂ + n + У >  0, '( a) e ^{1a|(n + y} ) ,        h ₂ + n + У <  0.

Анализ результатов. Оценим точность решения задачи о полуплоскости методом малого параметра с пятью членами разложения. Для этого сравним его с решением аналогичной задачи методом коллокации с 8 узловыми точками. Исследуем влияние составных геометрических и физических параметров Л = h и р = ( 4G 1 h 1 ( v -1 ) )/( aG ( v 1 -1 ) ) на точность решения. На рис. 1 представлены кривые расхождения методов для различных комбинаций μ и λ .

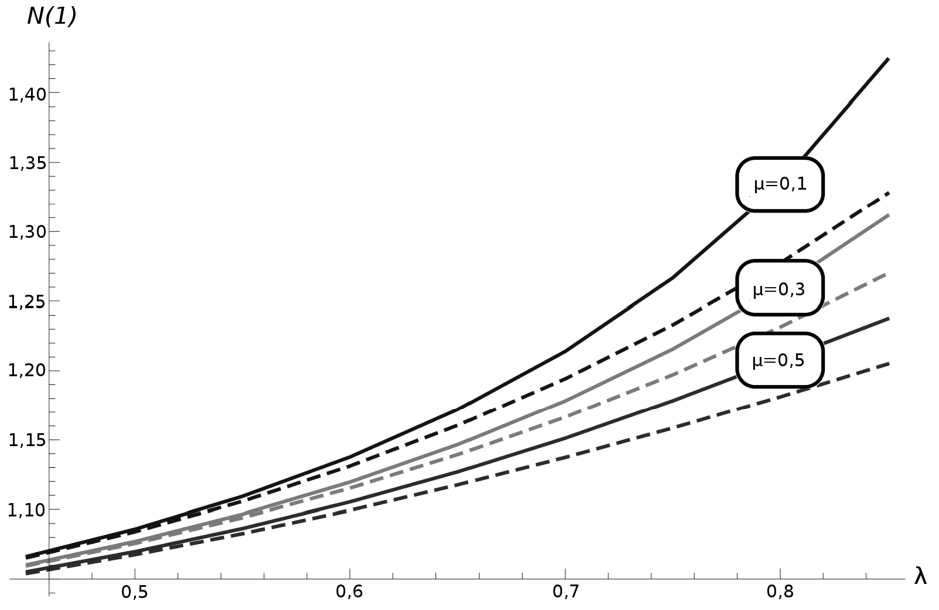
Рис. 1. Значения фактора влияния N (1), полученные методом малого параметра (сплошные линии) и методом коллокации (пунктирные линии) для различных комбинаций μ и λ

Экспериментально установлено, что решение задачи для полуплоскости методом малого параметра наиболее эффективно и целесообразно в диапазоне Л <0,7; ц <  0,7, т. к. даёт погрешность менее 5 %.

Учитывая разнообразие видов и технологий нанесения покрытий, важно провести многофакторный анализ их влияния на поведение трещин в подложке.

При численном анализе влияния накладки удобно ввести величину N ( z ) = K I ( z )/ K I „ ( z ) . Здесь K I ( z ) — коэффициент интенсивности нормальных напряжений в окрестности вершин трещины z = ± 1, K I „ ( z ) — соответствующая величина для случая такой же трещины в бесконечной упругой плоскости. N ( z ) , называемое фактором влияния [12], характеризует изменения напряжений, вносимые в рассматриваемую задачу границами сред и накладкой.

Следующие значения физических и геометрических параметров были приняты по умолчанию (модельная задача): E 1 / Е ₂ = 1,8; h / a = 1,5; h 1 / a = 0,01; h ₂ [a = 5 . Решения уравнений были построены методом коллокации с использованием 10 узловых точек.

Рассмотрим влияние толщины и жёсткости накладки при некоторых фиксированных значениях λ . Накладка существенно уменьшает интенсивность напряжений, особенно для больших и

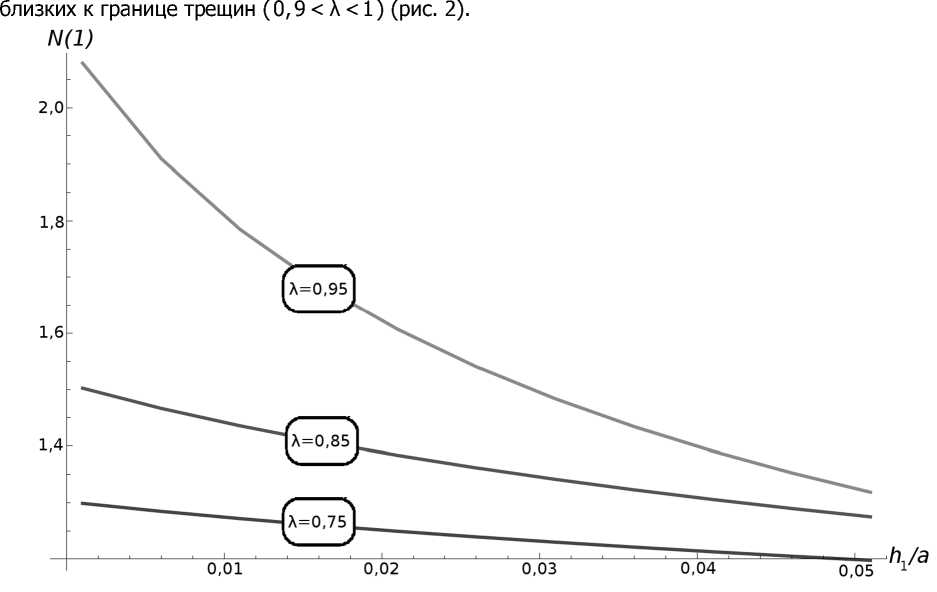
Рис. 2. Изменение фактора влияния в вершине трещины в зависимости от относительной толщины накладки

Далее проведём исследование влияния различных материалов покрытия на N ( 1 ) в зависимости от λ (рис. 3).

Анализ влияния накладки и различных вариантов граничных условий при y = - h ₂ для задачи о полосе представлен на рис. 4. На нижней грани действуют условия: A — гладкого контакта, B — жёсткой заделки, C — свободной границы. Случай отсутствия накладки отмечен как F (free).

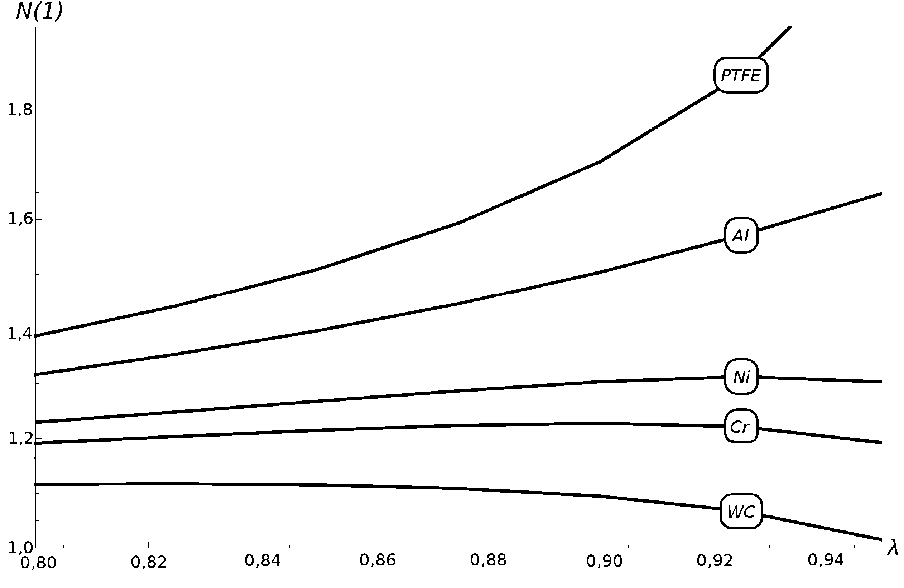
Рис. 3. Влияние материала накладки на интенсивность напряжений: PTFE — тефлон, Al — алюминий, Ni — никель,

Cr — хром, WC — карбид вольфрама

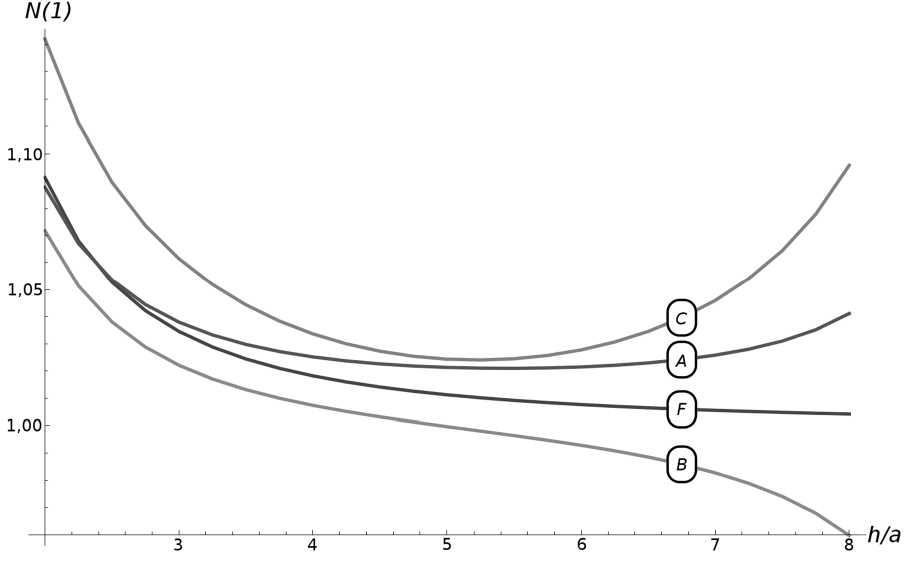
Рис. 4. Зависимость фактора влияния N(1) от относительной глубины трещины

При h₂ » а численные решения уравнения (19) совпадают с решением уравнения для полуплоскости (11).

Заключение. Решена задача определения критического состояния полубесконечных элементов конструкций, ослабленных внутренними поперечными трещинами и усиленных тонкими, гибкими накладками. Задачи о равновесии поперечной трещины в упругой полуплоскости и слое с накладками описаны интегральными уравнениями.

Во всех рассмотренных задачах сингулярно-дифференциальное уравнение имеет единую структуру, и сингулярная часть соответствует задаче об изолированной трещине в неограниченной упругой среде. Регулярная часть ядра интегрального уравнения в каждом конкретном случае характеризует взаимное влияние между трещиной и граничными поверхностями тела. Полученные интегральные уравнения были решены методами малого параметра и коллокации. Проведён анализ сходимости методов, получены численные результаты.