Влияние торсиального осциллятора на вероятность нетермического переноса электрона

В последнее десятилетие с помощью современных экспериментальных зондов и компьютерных расчетов для целого ряда донорно-акцепторных (ДА) систем были выявлены новые детали сложной динамики фотоиндуцированных процессов переноса зарядов [2; 14; 15; 18]. Это побудило исследователей вновь обратить внимание на ранее нерешенные теоретические вопросы [2; 4; 7; 9; 14], один из которых – отклонение от приближения Кондона (далее будем использовать термин «некондоновские» эффекты). Важность решения этого вопроса была осознана с первых дней разработки теории переноса электрона (ПЭ) в конденсированных средах [1; 6; 16]. В последние годы интерес к этой проблеме возрос, поскольку было показано, что для структурированных макромолекул с определенной гибкостью некоторых связей конфигурационные искажения могут привести к существенным изменениям параметра электронной связи [5; 12; 13, 17; 19–23].

В работе [17], используя квантово-химические методы, было проведено численное моделирование механизма фотоиндуцированного ПЭ с п-электронной группы тетрацена (донор) на п-элект-ронно-акцепторную группу пиромеллитимида, отделенную мостиком увеличивающегося размера (p-фенилен-виниленовый радикал олигомеров). В рамках теории Маркуса-Джортнера-Левича для мостиковой ДА-системы были рассчитаны основные параметры [10], влияющие на скорость термического ПЭ: параметр электронной связи между начальным и конечным состояниями Vel; энергия реорганизации среды Em и параметр экзотермичности реакции AG. Было показано, что в таких системах параметр электронной связи Vel зависит от ориентации и размера мостика. Кроме того, в рамках полностью квантово-механического подхода [11] было получено общее выражение для скорости неадиабатического термического ПЭ в ДА-мостиковых системах с учетом «некондоновских» поправок. Для двух конкретных моделей модуляции (экспоненциальной и линейной) было показано, что «некондоновские» эффекты могут привести к существенному росту скорости термического ПЭ в инвертированной области и к качественно новым зависимостям скорости от расстояния. Для ДА систем, в которой донор связан с акцептором мостиком, «некондоновские» эффекты связаны с скручивающим движением донорного и акцепторного фрагментов. Как показали экспериментальные и численные исследования [3; 24; 25], в гибких или полугибких ДА-мостиковых макромолекулах скручивающие эффекты могут быть значительными.

В рамках данной работы проведено теоретическое исследование влияния торсиальной моды, моделирующей скручивание ДА-системы, на сверхбыструю динамику фотоиндуцированного ПЭ с учетом отклонения от приближения Кондона. Используя нестационарную теорию возмущений, выполнен аналитический расчет вероятности нетермического ПЭ с учетом отклонения от приближения Кондона. Дана количественная оценка влияния «некондоновских» поправок для торси-ального осциллятора на динамику распада возбужденного состояния ДА-комплекса.

Расчет «некондоновских» поправок в реакциях нетермического переноса электрона

В дальнейшем будет рассмотрена модель ПЭ в ДА-системе в рамках двухуровневого приближения. Предполагается, что можно ограничиться рассмотрением только двух электронных состояний ДА-пары: состояние с переносом электрона | 1 ) и основное нейтральное состояние | 2 ) .

Гамильтониан рассматриваемой двухуровневой системы в рамках данной модели имеет вид:

H =

H V2 ) V21 H2 } где

H1 = 2 E[ Pa+«a X2 ]+2 [ P+^ фф ],

H 2 = 1 E[ Pa + - ' X a — X a 0 )2 ] + 1 [ РФ +^ Ф( Ф — Фе )2]+AG(2)

2 a

– гамильтонианы колебательной подсистемы в состоянии с ПЭ (1) и в основном нейтральном состоянии (2). Здесь A G и E rm = E Aj 2to „ — свободная энергия и энергия реорганизации среды. Параметры X_a , P_a , o_a и A_a = ® a X _{a 0} — координаты, импульсы, частоты и константы электрон-колебательной связи для нормального колебания термостата с индексом а , соответственно. Второе слагаемое в (1), (2) описывает торсиальное вращательное движение в гармоническом приближении, вызванное скручиванием донорного и акцепторного фрагментов относительно мостика. Параметры торсиального осциллятора соответственно равны Р ф , ф, Q ф , А ф =^ ф Ф о . Здесь и далее используется система единиц, в которой постоянная Планка h = 1. Кроме того, считается, что матричный элемент перехода между состояниями 1 и 2 рассматриваемой системы V 12 = V ₂₁ = V el является действительным и зависит только от координаты торсиального осциллятора ф [9]:

Vel = V 0 + V 1 ^ехРИФ).

Эволюция рассматриваемой системы описывается уравнением Лиувилля для статистического оператора ρ idри =[H,p]ki, k,l=1,2.

В дальнейшем процесс фотовозбуждения явно не рассматривается, а считается, что система в результате вертикального перехода из основного состояния с равновесной колебательной подсистемой уже перешла на возбужденный терм [8]. Предполагая длительность импульса малой по сравнению с характерными временами ядерной подсистемы, мы можем рассматривать ядерную подсистему (все колебательные моды, включая торсиальную) замороженной на протяжении действия импульса и записать начальное условие для диагональных элементов матрицы плотности в виде [8]

C 1(0) = Рф ||J^ath(emj2) απ exp ]-4a [C°th ( в®«/2 )( Xa - Xa )2 th ( вОф/2 ) (Xa + Xa - 2 Aa^)2 ]|

Яд

Р ф =V "^ th ( Р П ф/ 2 ) exp

q

- 2 A /П, ² ) ² ]

^{ф ф} 7 ]

- “ф [co th (вПф/2) (Ф—Ф')2 + th (во/2) (Ф+Ф где в = 1/kBT;

k _B – постоянная Больцмана;

T – температура.

Во втором порядке теории возмущений по параметру электронной связи вероятность быстрого обратного переноса электрона из состояния 1 в состояние 2, протекающего до установления термодинамического равновесия растворителя (нетермический ПЭ), определяется выражением [8]

W12 ( t) = SP [ Р11 ( t )] = SP [ Р22 ( t )] = t          t1

= J dt i J dt ₂ Sp ^[ V 21 ⁽ t i ) e - iH ^{1 (} t - ‘ ² ) Р и ⁽ t 2 ) V ,2 ⁽ t 2 ) C H 2 ⁽ t ^{1 -} t ² ) ] oo

t t 1

+ J ^dt 1 J dt 2 Sp ^[ e - iH ^{2 (} t ^{1 -} t ² ) V 21 ( t 2 ) Р ц ( t 2 ) б” ^{1 (} t ^{1 -} t ² ) V 1₂ ( t 1 ) ]

oo

Вычисляя след операторов в формулах (3), для вероятности нетермического ПЭ с учетом «некондоновских» поправок получаем:

t^t 1

W 12 = SP ^[ Р 11^{2 ) (} t ) ] = V >2 Re J ^dt 1 J ^dt 2 ^exP { i ^A G ⁽ t 1 ^- t 2 ) } F bath ⁽ t 1 , t 2 ) F( 6 ^{( t} 1 , t 2 ) ,

где вклад термостата описывает функция [8]

F. ( t ,, L ) = exp iiYA^v Г- sin ® ( t, - L ) + 2 (sin to t, - sin to t , Я bath 1 , 2^d * O 3 L            a ^A 1      2^d \ a 1             a 2 /]

I a 2toa f A2 z                           J

X exp Z-E - a -^COth ( ^e ® a /2 ) [ ^{1 - co}s to a ⁽ t 1 ^- t 2 ) ] ^ ,

I a 2toa                                           J а вклад торсиального осциллятора c учетом отклонения от приближения Кондона – функция Fφ. Функцию Fφ удобно факторизовать, выделив вклад «некондоновских» поправок

I E . г                                       mJ

F ф ( t i ,t 2 ) = exp 1 + i Q- |_-sinQ ф ( 1 1 — t 2 ) + 2 ( sinQ/ 1 - smQ/ 2 ) ] r

L ^{Q ф}

exp J -coth(PQф/2)(1-cos<1(ti -t2)) r[i+a, ф(X;0) + Ai ф(0;X) + A2f(X;2)] , L Qф                                 J где E^ = A22[2Q ф, A, = ViV , b (t i, t2) = -( A, /Q ф)(cos Q „t - cos Q ф2),

аф(t i, t2) = (Аф M) (sin Qфti - sin Ц^2 ),

fф(n,5) = exp{52 sin(2Qф(ti -t2))/4Qф -(Аф/Qф)[П + 5cosQф (ti -t2)]} exp{ 5 cosQ ф ( ti - t 2 ) Ьф ( ti, t 2)/2 - 5аф (ti, t 2)sin (Q ф ( ti - t 2 ))/2Q ф - Ьф ( ti, t 2 ) П/2} exp{coth (вТф /2) [n 2 + 52 + 2n + 5 cos Qф (t1 -12)] / 4Qф}

I                           5

exP I ^- i coth ( ^{в Т} ф /2 ) 2b^Ь ф ⁽ t i , t 2 ) sin ^Q ф ( t _]

^- t 2 ) ^{+ а} ф ⁽ t i , t 2 ) ^[ П ^{+ 5} cos ^Q ф ( t i ^- t 2 ) ] / ^{2 Q} ф

Для идеального полярного растворителя, описываемого моделью Дебая

π A ²

2ErmωτL i + to2T2 ’

J ⁽ ® ) = tZ ^ ^ ⁽ ® ^- ® a ) =

2 α ωα для расчета вероятности нетермического ПЭ с учетом «некондоновских» поправок (4)–(6) можно воспользоваться приближением высоких температур coth(в®/2)^2/в®, ^^Тт£>>i. В пределе ErkgTг £ >>i все косинусы и синусы в формулах (5)-(6) можно разложить в ряд по аргументу (t1-t2) до второго порядка включительно. В результате для вероятности нетермического ПЭ получим где

W i2 = V o² ( W iF +A i W i2ⁱ +AW 2² ) ,

W F^C ( t ) = ^nL-

¹² E _r k _B T

t j exp 0

Q ²( τ )

4 E r k B T

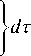
– вероятность нетермического ПЭ в приближении Кондона [8], а «некондоновские» поправки имеют вид

A W® = exp { - ХА ф /Q ф + ( kT 2 ²/2Q ф ) } *

π

EkT rB

t

Re j exp

[ Q ( t i ) + A Q ( 1 1 ) + ( iXA фj 2Q ф ) sm Q ф t i ]²

4 EkT rB

> dt _i ,

A W (3) = exp { - X 2 А ф /Q ф + ( 2 k _B TX^ Т ф ) }

-___________________ [ Q ( t i ) +^A Q ( t i ) ] ____________________J _dt

4 E_rk_BT [ i - Х А _ф [ i - cos Q t _i ] / ( 8 k_BTE_r ) - 2 /8 E_r ] J ⁱ

Здесь введены обозначения Q ( t ) = - A G - E_r + 2 E rm exp {- 1 / t _l } + 2 E r ^ cos Q ф , E r = E rm + E_rф, A Q ( t _i) = X ( A ^ k B T / Q ₀ ²)cos Q t _i - 2 2 /2.

Приближенные аналитические выражения (9)–(10) позволяют количественно оценить масштаб влияния «некондоновских» поправок на вероятность нетермического ПЭ и на динамику распада возбужденного состояния ДА-комплекса, сформированного вследствие фотовозбуждения комплекса коротким лазерным импульсом на частоте полосы с переносом заряда. Численные расчеты проводились в рамках Дебаевской модели с одним временем релаксации tl= 1 пс. Энергия реорганизации во всех расчетах полагалась равной Er = Erm + Er^= 1 эВ, что характерно для сильных полярных растворителей. Параметр электронной связи V0 варьировался в диапазоне от 0,01 до 0,02 эВ. Величина свободной энергии реакции при этом задавалась на интервале от -0,5 до 0,5 эВ. Численные расчеты поправок по формулам (9)–(10) показали, что при комнатных температурах вероятность нетермического ПЭ может увеличиться приблизительно на 10 %, что ускоряет распад возбужденного состояния ДА-комплекса. Для определения области всех параметров, где «некондоновские» поправки могут существенно повлиять на динамику обратного ПЭ, требуется более детальный численный анализ не только приближенных формул (9)–(10), но и формул (4)–(6), что планируется сделать в дальнейшем.