Влияние твердости бетона гидрозатвора каменной дамбы на ее напряженно-деформированное состояние

Introduction . It is known that at durable loads accommodation the concrete deformation modulus becomes 2÷3 times as less due to creep. The study fulfilled by the author permitted assessing the impact of stress relaxation in concrete of rockfill dam seepage-control face on its stress-strain state (SSS). Materials and methods. SSS was studied with the aid of numerical modeling by the finite element method. There was considered a 100 m high dam. Calculations were conducted for a wide range of variations of rockfill linear deformation values (from 60 to 480 МPа) and two values of its Poisson’s ratio (0.2 and 0.3). Various alternatives of under-face zone structural designs were considered. Modeling was made of shear characteristics decrease in the contact between the face and concrete bedding due to the arrangement of a bitumen mastic layer. Results . It was established that concrete linear deformation value Eb differently affects bending moments and longitudinal forces in the face. Decrease of Eb predominantly decreases bending moments from the face cross bending deformations but has a small impact on the longitudinal forces in it and bending moments from longitudinal bending deformations. Bending moments of cross bending are nearly in direct proportion with value Eb . Conclusions. The processes of creep and stress relaxation in concrete has a favorable effect on the face crack resistance because they decrease stresses in concrete. However, the value of stresses in the face concrete is not in direct proportion with concrete linear deformation modulus value Eb . It was established that the decrease of Eb by 60% decreases tensile stresses in the face concrete by approximately 30%. To decrease the risk of cracking in the face the quick reservoir impoundment is not recommended. In the analysis of concrete face rockfill dam structural design it is quite justified to analyze SSS at modulus Eb corresponding to its initial value without consideration of concrete creep because this case is more dangerous.

Для гидротехнического строительства актуально научное обоснование конструкций каменно-набросных плотин с железобетонным экраном. В настоящее время в мире построено несколько десятков сверхвысоких плотин данного типа [1-2] и рассматриваются перспективы их применения при высоте 250÷300 м [3-5].

Для обоснования возможности строительства этих плотин проводятся исследования напряжённо-деформированного состояния плотин [6-15].

На напряженно-деформированное состояние бетонного экрана каменно-набросной плотины оказывает влияние множество разных факторов. Прежде всего, это деформативные характеристики каменной наброски.

Результаты численного моделирования напряженно-деформированного состояния показывают, что в экране возникают значительные растягивающие напряжения, которые превышают прочность бетона на растяжение [6, 16, 17]. Автором было получено, что обеспечить прочность бетона на растяжение чрезвычайно сложно [18, 19]. Даже при очень тщательном уплотнении каменной наброски, применении армирования в бетоне экрана возникают растягивающие напряжения. Это подтверждается многочисленными фактами повреждений экранов ряда сверхвысоких плотин [20, 21].

Однако в исследованиях [15-19] использовалось значение модуля линейной деформации бетона экрана E б =29÷30 ГПа, которое соответствует т.н. начальному модулю, т.е. модулю на момент приобретения нормативной прочности. Свод правил СП 41.13330.2012 (Russian Building Code SP 41.13330.2012 “Concrete and reinforced concrete hydraulic structures”), регламентирующий вопросы проектирования бетонных конструкций гидротехнических сооружений, других значений модуля деформации бетона не предусматривает. Это значение принимают в своих исследованиях и другие исследователи [10-12]. Однако значение начального модуля бетона E б соответствует быстрому восприятию нагрузок, а при длительном действии нагрузок значение модуля E б существенно уменьшаться. Соответственно, можно ожидать, что за счёт процессов релаксации напряжения в бетоне могут быть уменьшены.

Это ставит под сомнение полученные в наших исследованиях выводы об отсутствии гарантий трещиностойкости бетонных противофильтрационных экранов. Поэтому автором были выполнены исследования по оценке влияния деформативных свойств бетона экрана на его напряженно-деформированное состояние, результаты которых описаны в данной статье.

В этом исследования использовались данные Свода правил СП 63.13330.2012 (Russian Building Code SP 63.13330.2012 “Concrete and won concrete construction. Design requirements”). В нём установлены правила определения модуля линейной деформации бетона для случая продолжительного действия нагрузки. В соответствии с табл.6.12 Свода правил модуль бетона класса B30 уменьшается примерно в 2,6 раза. Таким образом, можно ожидать, что значение модуля линейной деформации бетона составит 11,1÷11,5 ГПа.

2    Materials and Methods

Исследования проводились на примере плотины высотой 100 м с заложением откосов 1,3 (рис. 1). Строение упорной призмы плотины принималось однородным.

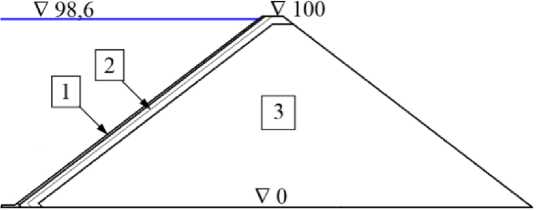
Рис. 1. Схема конструкции каменно-набросной плотины с бетонным экраном.

1 – бетонный экран, 2 – подэкрановая зона, 3 – упорная призма

• Fig. 1. Design diagram of a concrete faced rockfill dam.

• 1    - concrete face, 2 - sub-face area, 3 - thrust prism

Исследования напряженно-деформированного состояния плотины проводились с помощью численного моделирования методом конечных элементов. Использовалась вычислительная программа, составленная автором [20].

Составленная конечно-элементная модель поперечного сечения плотины включала 871 конечный элемент сплошной среды. Периметральный шов и контакт экрана с телом плотины моделировались с помощью 106 конечных элементов типа Goodman. Предусматривалась возможность потери прочности контакта на растяжение или сдвиг. Сопротивление сдвигу описывалось по теории Кулона. В конечно-элементной модели использовались с кубической степенью аппроксимации перемещений внутри элемента, что позволило довольно точно воспроизвести сложный характер работы бетонного экрана и его взаимодействия с телом плотины. Общее количество степеней свободы в модели составило 8586.

Исследования проводились для двух расчётных схем (вариантов).

• 1.    Условная расчётная схема, в которой экран укладывается непосредственно на подэкрановую зону из щебенистого грунта. В этом случае параметры сдвиговой прочности на Sainov, M.P.

• 2.    Расчётная схема, соответствующая конструкции современных плотин. В них откос плотины под экраном формируется из бетонных блоков, образуя бетонную подготовку. При этом контакт между экраном и подэкрановая подготовкой покрывается битумной эмульсией для снижения трения. Параметры сдвиговой прочности контакта учитывали мероприятия по снижению трения: удельное сцепление принималось равным 20 кПа, а угол внутреннего трения 10 ° . Касательная жёсткость контакта была принята равной 50 МПа/(пог.м).

Impact of concrete hardness of rockfill dam seepage-control face on its stress-strain state;

контакте экрана с подэкрановой зоной принимались соответствующими контакту бетона и каменной наброски: удельное сцепление равно 0, угол внутреннего трения 45 ° . Касательная жёсткость контакта принималась равной 200 МПа/м.

В исследовании грунты тела плотины считались линейно-деформируемыми. Они проводились для широкого диапазона значений параметров модели. Модуль линейной деформации E к каменной наброски варьировался от 60 до 480 МПа. Этот диапазон значений соответствует деформируемости каменной наброски в теле реальных плотин [23, 24, 1]. Расчёт проводился для двух вариантов значения коэффициента Пуассона V k каменной наброски: 0,2 и 0,3.

Принималось, что экран выполнен из бетона класса B30. В нашем исследовании рассматривались два варианта значения модуля линейной деформации бетона E б : 29 ГПа и 12 ГПа. Коэффициент Пуассона бетона принимался V 6 =0,2. Расчётное сопротивление бетона по предельным состояниям второй группы в соответствии с упомянутым ранее СП 41.13330.2012 принималось равным 1,8 МПа.

Расчёты проводились на нагрузки собственного веса и гидростатического давления. Моделировалась самая простая схема последовательности возведения сооружения и нагружения его внешними силами. Сначала воспроизводилась послойная отсыпка каменной наброски, затем укладка бетонного экрана, а потом – постепенное наполнение водохранилища.

3    Results and Discussion

Анализ результатов решения задачи напряженно-деформированного состояния проводился по величинам перемещений и напряжений экрана, а также по вычисленным через напряжения продольным силам и изгибающим моментам в сечениях бетонного экрана.

Для всех вариантов характерна качественно похожая картина напряженно-деформированного состояния бетонного экрана. Рассмотрим её основные характерные особенности в распределении перемещений и напряжений.

Первая особенность состоит в деформациях поперечного изгиба бетонного экрана. Перемещения экрана в направлении поперёк к откосу (U n , «прогибы») распределены таким образом, что экран изгиб в сторону нижнего бьефа (рис. 2). Изгиб вызывает растяжение низовой грани экрана и сжатие верховой. Максимум прогибов экрана достигается, как правило, на 7 45м, поэтому в нижней части экрана изгиб интенсивнее, чем в верхней.

Величина максимального прогиба U n экрана определяется прежде всего величиной модуля линейной деформации каменной наброски Е к , но также зависит от её коэффициента Пуассона V k , а также от конструкции подэкрановой зоны. При V k =0,3 максимальный прогиб на 8^9% меньше, чем при V k =0,2. Наличие бетонной подэкрановой подготовки уменьшает максимальный прогиб примерно на 3%. Влияние модуля деформации бетона экрана на прогибы незначительно.

Вторая особенность состоит в наличии линейных деформаций укорочения-удлинения. Дело в том, что экран получает продольные перемещения U t , т.е. перемещения в направлении вдоль откоса. Они направлены от подошвы к гребню, при этом происходит раскрытие периметрального шва. Продольные перемещения U t возникают благодаря силам трения на границе экрана и тела плотины. Также как и силы трения, U t неравномерно распределены по длине экрана.

Силы трения вызывают появление в экране продольных линейных деформаций и, соответственно, продольных сил. Во всех вариантах на нижнем участке экрана испытывает деформации удлинения, а на верхнем – укорачивания.

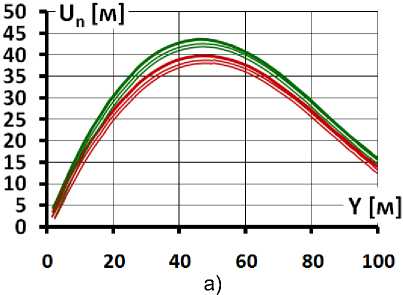
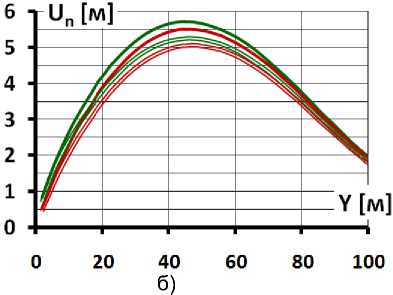
0.2 : без подготовки —0.3 : без подготовки = 0.2 : с подготовкой = 0.3 : с подготовкой

Рис. 2. Прогибы экрана в различных вариантах устройстве подэкрановой зоны и модуля деформации каменной наброски, а – при E к =60 МПа; б – при E к =480 МПа

Fig. 2. Deflections of the face in various versions of the device of the sub-face zone and the module of deformation of the stone outline, a - at Ek = 60 MPa; b - at Ek = 480 MPa

Трение между экраном и бетонной подготовкой оказывает на напряженно-деформированное состояние бетонного экрана ещё один эффект, он заключается в продольном изгибе экрана. Продольный изгиб возникает в результате эксцентриситета приложения продольных сил. В большинстве поперечных сечений экрана сила трения на контакте и продольная сила в экране равны друг другу. Но в сечениях нижнего края экрана равенство не наблюдается из-за наличия в нём касательных напряжений. Продольный изгиб приводит к существенному росту растягивающих напряжений на низовой грани экрана и сжимающих на верховой грани. Однако он имеет локальный эффект и распространяется только на нижних 8 м высоты экрана.

В вариантах с бетонной подготовкой за счёт снижения трения между экраном и подготовкой (схема 2) продольный изгиб развит существенно слабее.

Продольный и поперечный изгиб, а также развитие продольных сил определяют величину и характер распределения напряжений в экране. Наибольший интерес представляют продольные напряжения, т.е. напряжения, действующие в направлении вдоль откоса. Их распределение по граням и высоте экрана показано на рис. 3-6 на примере двух крайних вариантов: E к =60 МПа, E к =480 МПа.

Анализ показывает, что напряженно-деформированное состояние бетонного экрана в большинстве случаев является неблагоприятным. Из-за продольно-поперечного изгиба и наличия растягивающих продольных сил для экрана характерны растягивающие напряжения. Наиболее неблагоприятное напряженно-деформированное состояние складывается на нижнем участке экрана. Здесь действуют растягивающие продольные силы, а также максимальны деформации поперечного изгиба экрана. Кроме того, существенное негативное влияние оказывает продольный изгиб.

В большинстве случаев растягивающие продольные напряжения на нижнем участке экрана превышают расчётное сопротивление бетона на растяжение. Однако в при устройстве слоя «смазки» (схема 2) растягивающие напряжения несколько меньше, чем при подэкрановой зоне из грунта (схема 1).

5 _G [МПа] g -г<>[МПа

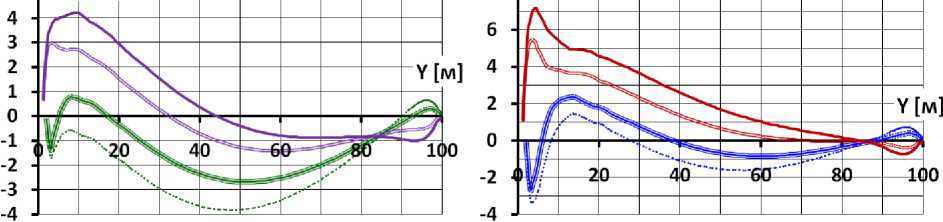
а) ν к =0,2                                          б) ν к =0,3

12 ГПа: верховая = 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

12 ГПа: верховая    —= 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

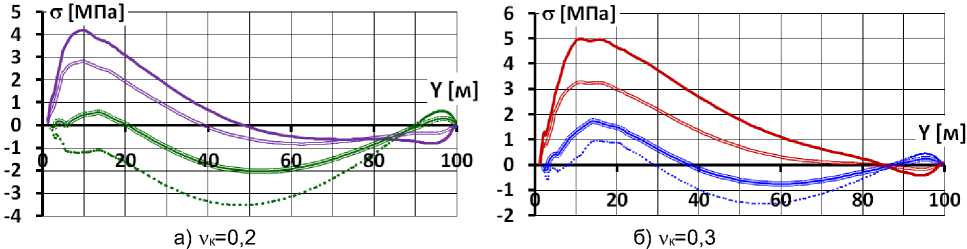
Рис. 3. Продольные напряжения на верховой и низовой гранях экрана в расчётных вариантах с E к =60 МПа и при отсутствии бетонной подготовки

Fig. 3. Longitudinal stresses on the upper and lower faces of the face in design options with E k = 60 MPa and in the absence of concrete blinding coat

12 ГПа: верховая = 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

12 ГПа: верховая    —= 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

Рис. 4. Продольные напряжения на верховой и низовой гранях экрана в расчётных вариантах с E к =60 МПа и при наличии бетонной подготовки

2.5 -гС>[МПа

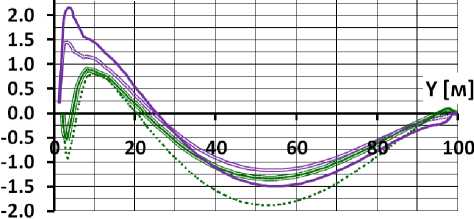
а) ν к =0,2

12 ГПа: верховая = 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

Fig. 4. Longitudinal stresses on the upper and lower faces of the face in design options with E k = 60 MPa and in the presence of concrete blinding coat

б) ν к =0,3

12 ГПа: верховая    —= 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

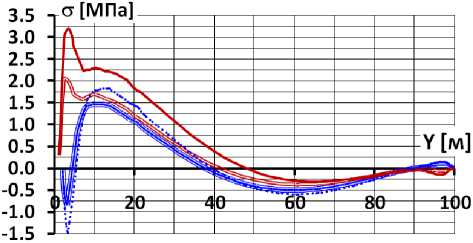
Рис. 5. Продольные напряжения на верховой и низовой гранях экрана в расчётных вариантах с E к =480 МПа и при отсутствии бетонной подготовки

• Fig. 5.    Longitudinal stresses on the upper and lower faces of the face in design options with

E k = 480 MPa and in the absence of concrete blinding coat

12 ГПа: верховая = 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

12 ГПа: верховая = 12 ГПа: низовая

29 ГПа: верховая —29 ГПа: низовая

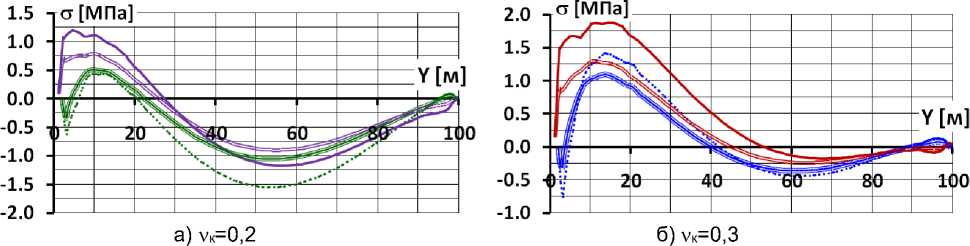
Рис. 6. Продольные напряжения на верховой и низовой гранях экрана в расчётных вариантах с E к =480 МПа и при наличии бетонной подготовки

• Fig. 6.    Longitudinal stresses on the upper and lower faces of the face in design options with

E k = 480 MPa and in the presence of concrete blinding coat

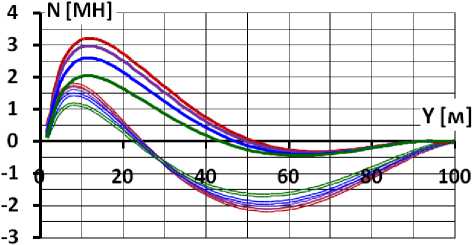
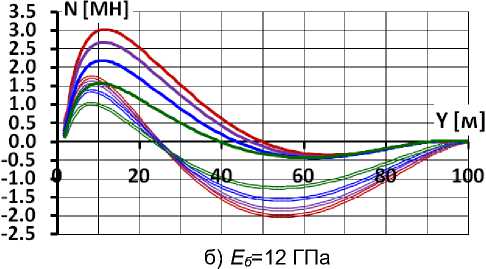
Сравнение напряженно-деформированных состояний разных вариантов позволило оценить влияние на напряженно-деформированное состояние бетонного экрана деформативных характеристик бетона и каменной наброски. Этот анализ можно провести с помощью рис. 7-8, на которых для разных вариантов показаны значения изгибающего момента M, и рис. 9-10, на которых показано распределение продольных сил N.

На рис. 7-8 видно, что в нижней части экрана действуют растягивающие продольные силы, а в верхней – сжимающие. Характер распределения продольных сил N определяется в основном коэффициентом Пуассона ν к каменной наброски. При ν к =0,2 участок растягивающих продольных сил распространяется примерно до ∇ 25 м, а при ν к =0,3 – до ∇ 50 м. Интенсивность N определяется как ν к , так и E к . Кроме того, в вариантах с бетонной подготовкой растягивающие продольные силы менее интенсивны за счёт снижения трения между экраном и подготовкой.

а) E б =29 ГПа

60 МПа - 0.2 = 120 МПа - 0.2 = 240 МПа - 0.2 = 480 МПа - 0.2

60 МПа-0.3 —120 МПа-0.3 —240 МПа-0.3 — 480 МПа - 0.3

Рис. 7. Распределение продольных сил по высоте экрана при отсутствии бетонной подготовки

В условных обозначениях вариантов первая цифра соответствует модулю деформации каменной наброски E к , а вторая цифра – коэффициенту Пуассона каменной наброски ν к

• Fig. 7.    The distribution of longitudinal forces along the height of the face in the absence of concrete blinding coat

In the legend of the variants, the first digit corresponds to the modulus of deformation of the stone outline E к , and the second digit corresponds to the Poisson's ratio of the rock blanket ν к

60 МПа - 0.2 = 120 МПа - 0.2 = 240 МПа - 0.2 = 480 МПа - 0.2

60 МПа-0.3 —120 МПа-0.3 —240 МПа-0.3 — 480 МПа - 0.3

Рис. 8. Распределение продольных сил по высоте экрана при наличии бетонной подготовки В условных обозначениях вариантов первая цифра соответствует модулю деформации каменной наброски E к , а вторая цифра – коэффициенту Пуассона каменной наброски ν к

• Fig. 8.    The distribution of longitudinal forces along the height of the face in the presence of concrete blinding coat

In the legend of the variants, the first digit corresponds to the modulus of deformation of the stone outline E к , and the second digit corresponds to the Poisson's ratio of the rock blanket ν к

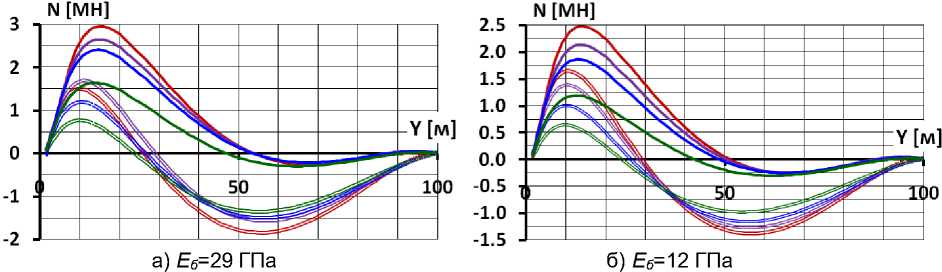
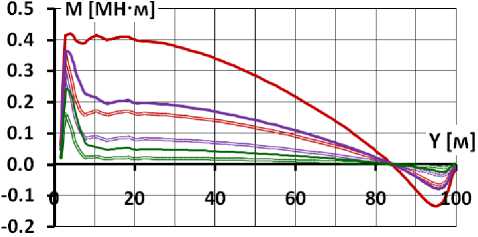
Распределение изгибающих моментов M по высоте экрана (рис. 9, 10) хорошо иллюстрирует эффект продольного изгиба экрана. Видно, что на самом нижнем участке экрана значения изгибающего момента резко возрастают, несмотря на отсутствие ярко выраженного увеличения прогибов. Этот скачок моментов является следствием продольного изгиба. В схеме 1 (рис. 9) влияние продольного изгиба на M более существенно, чем поперечного изгиба. В схеме 2 (рис. 10) благодаря снижению сил трения на контакте экрана с подэкрановой подготовкой увеличение моментов из-за продольного изгиба мало.

а) ν к =0,2

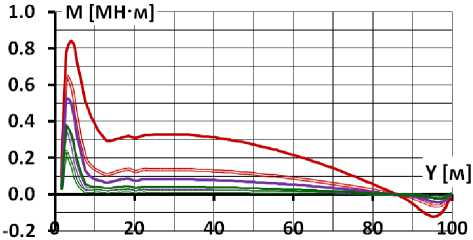
б) ν к =0,3

12 ГПа-60 МПа   = 12 ГПа -120 МПа = 12 ГПа - 480 МПа

29 ГПа - 60 МПа   — 29 ГПа -120 МПа — 29 ГПа - 480 МПа

Рис. 9. Распределение изгибающих моментов по высоте экрана при наличии бетонной подготовки

В условных обозначениях вариантов первая цифра соответствует модулю деформации бетона E б , а вторая – модулю деформации каменной наброски E к

• Fig. 9.    The distribution of bending moments along the height of the face in the presence of concrete blinding coat

In the designations of the options, the first digit corresponds to the concrete deformation modulus E b , and the second digit corresponds to the rock blanket deformation modulus E k

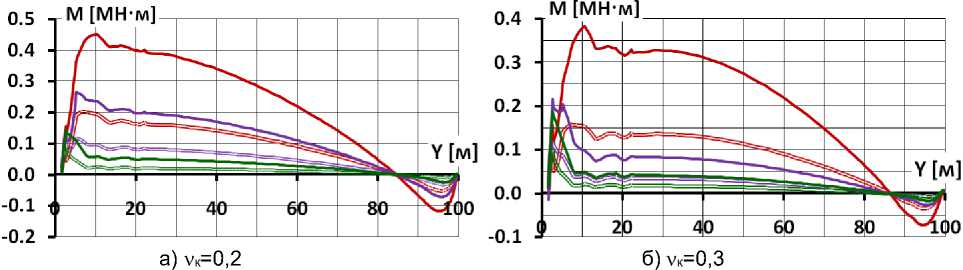
12 ГПа-60 МПа   = 12 ГПа -120 МПа = 12 ГПа - 480 МПа

29 ГПа-60 МПа   — 29 ГПа -120 МПа — 29 ГПа - 480 МПа

Рис. 10. Распределение изгибающих моментов по высоте экрана при отсутствии бетонной подготовки

В условных обозначениях вариантов первая цифра соответствует модулю деформации бетона E б , а вторая – модулю деформации каменной наброски E к

• Fig. 10.    The distribution of bending moments along the height of the face in the absence of concrete blinding coat

In the legend of the options, the first digit corresponds to the concrete deformation modulus E b , and the second digit corresponds to the deformation modulus of the rock blanket E k

Анализ рис. 9 показывает, что деформации продольного изгиба мало зависят от E к . Изгибающий момент от продольного изгиба определяется силами трения на контакте бетонного экрана с телом плотины, поэтому в большей степени зависят от ν к . По этой причине с ростом E к роль продольного изгиба в формировании напряженно-деформированного состояния бетонного экрана увеличивается.

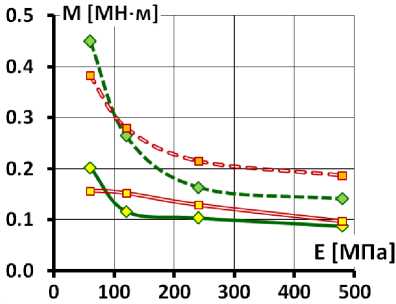
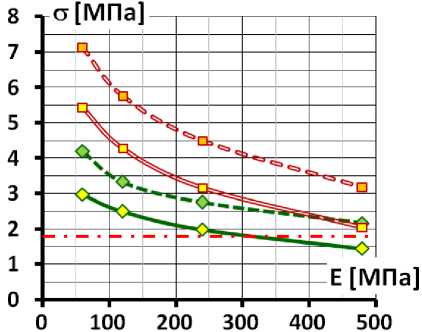
Анализ влияния на напряженно-деформированное состояние бетонного экрана параметров деформируемости каменной наброски можно провести с помощью рис. 11, 12, на которых показано изменение максимальных значений изгибающего момента M max (рис. 11) и растягивающей продольной силы N max (рис. 12) от величин E к , ν к , E б .

Анализ позволил выявить, что степень влияния факторов на величины продольных сил, напряжений от продольного и поперечного изгиба различна.

• •    Величина коэффициента Пуассона каменной наброски ν к оказывает существенное влияние на напряженно-деформированное состояние бетонного экрана. Увеличение ν к приводит к росту изгибающего момента и продольной силы. Увеличение ν к с 0,2 до 0,3 ведёт в большинстве случаев увеличивает M max и N max в 1,5÷2 раза.

• •    Величина модуля деформации каменной наброски E к в основном определяет количественные параметры напряженно-деформированного состояния бетонного экрана. При этом E к в большей степени влияет на изгибающие моменты, чем на продольные силы. Изгибающие моменты от поперечного изгиба прямо пропорциональны величине E к . А увеличение E к в 4 раза уменьшает продольные силы на треть в схеме 1 и вполовину в схеме 2. По этой причине при высоких E к роль деформаций поперечного изгиба в формировании напряженно-деформированного состояния бетонного экрана резко снижается по сравнению с деформациями продольного удлинения.

Хорошо видно, что в схеме 2 максимальные значения моментов M max примерно в 2 раза меньше, чем в схеме 1 (рис. 12). В то же время максимальные значения продольных сил N max в схеме 2 не намного меньше, чем в схеме 1 (рис. 11).

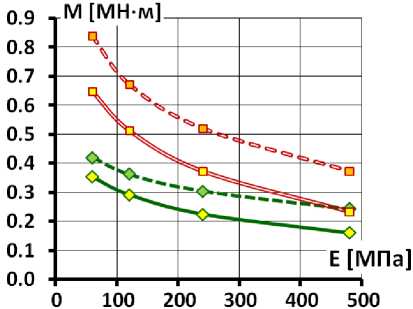
Также с помощью рис. 11, 12 можно оценить влияние величины модуля деформации бетона E б на M max и N max . На них хорошо видно, что при снижении E б с 29 ГПа до 12 ГПа происходит снижение M max и N max . При этом влияние E б на продольные силы N max невелико при ν к =0,2, а при ν к =0,3 и снижает N max примерно на 0,5 МПа (рис. 11). Максимальное снижение N max составляет 23%. Влияние E б на изгибающие моменты M max различается в зависимости от схемы сопряжения экрана с плотиной. В схеме 1 M max снижается на 15÷35%, а в схеме 2 снижается на 40÷60% (рис. 12).

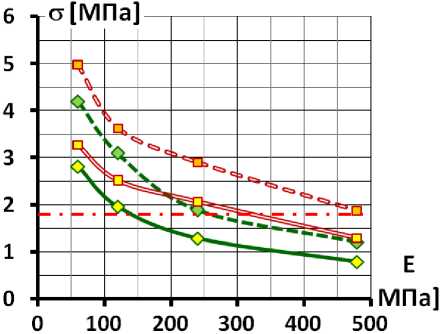
На рис. 13 позволяет оценить влияние E б на максимальные значения растягивающих продольных напряжений в экране. Во всех случаях снижение E б с 29 ГПа до 12 ГПа приводит к заметному снижению растяжения – на 30÷35%. При этом следует отметить, что изменения напряженно-деформированного состояния экрана, вызванные снижением E б , оказались не столь значительны, как можно было бы ожидать. Снижение E б почти в 2,5 раза (на 60%) уменьшает растягивающие напряжения лишь примерно на треть.

Тем не менее, эти изменения существенны с точки зрения обеспечения трещиностойкости экрана. Например, в схеме 1 при E б =29 ГПа ни в одном из вариантов прочность бетона на растяжение не обеспечивалась, но при E б =12 ГПа прочность обеспечивается при E к >300 МПа (и ν к =0,2) (рис. 13). В схеме 2 при E б =29 ГПа прочность на растяжение обеспечивается при E к >260 МПа и ν к =0,2, а также при E к >500 МПа и ν к =0,2. При E б =12 ГПа прочность выполняется при меньших значениях E к : при E к >140 МПа и ν к =0,2, а также при E к >330 МПа и ν к =0,2.

Однако следует отметить, что оба значения модуля линейной деформации E б (29 ГПа, 12 ГПа) возможны в реальных условиях. При быстром наполнении водохранилища, когда гидростатическое давление на экран резко увеличивается, а каменная наброска начнёт уплотняться интенсивно, модуль линейной деформации E б будет соответствовать случаю быстрого восприятия нагрузок ( E б =29 ГПа). Известен случай, когда в экране плотины Mohale при быстром наполнении водохранилища возникла трещина [25]. Правда, в этом случае трещина возникла из-за потери прочности бетона на сжатие. Опасность представляет также первое наполнение водохранилища, когда деформации каменной наброски протекают в условиях активного нагружения и наиболее значительны. Известно, что образование трещин в экранах плотин Barra Grande, Campos Novos происходило именно при первом заполнении водохранилища [20, 21].

Можно сказать, что случай с E б =29 ГПа является вполне возможным и наиболее опасным расчётным случаем.

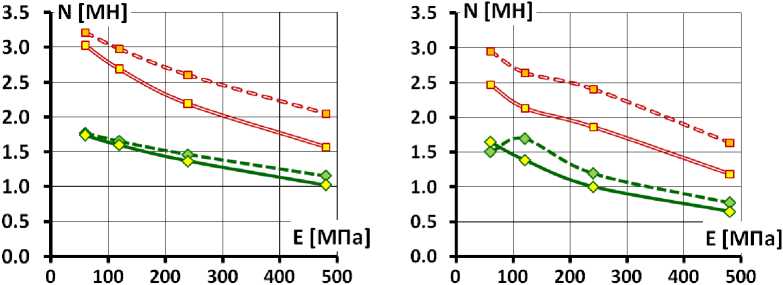
а)                                           б)

О 29 ГПа, v=0.2    -С- 12 ГПа, V =0.2    -о- 29 ГПа, v=0.3    о 12 ГПа, v =0.3

Рис. 11. Изменение максимальных значений продольных растягивающих сил в экране в зависимости от модуля деформации каменной наброски а – схема 1 (при отсутствии бетонной подготовки), б – схема 2 (при наличии бетонной подготовки)

• Fig. 11.    Change in maximum values of longitudinal tensile forces in the face depending on the modulus of deformation of the rock blanket

a - scheme 1 (in the absence of concrete blinding coat), b - scheme 2 (in the presence of concrete blinding coat)

а)

б)

■О 29 ГПа, v=0.2 О 12 ГПа, v=0.2 с» 29 ГПа, v=0.3 о 12 ГПа, v =0.3

Рис. 12. Изменение максимальных значений изгибающих моментов в экране в зависимости от модуля деформации каменной наброски а – схема 1 (при отсутствии бетонной подготовки), б – схема 2 (при наличии бетонной подготовки)

а)

Fig. 12. Changing the maximum values of bending moments in the face depending on the modulus of deformation of the rock blanket a - scheme 1 (in the absence of concrete blinding coat), b - scheme 2 (in the presence of concrete blinding coat)

б)

■О 29 ГПа, v=0.2   -012 ГПа, v =0.2

*п-29 ГПа, v=0.3 о 12 ГПа, v =0.3   — ограничение

Рис. 13. Изменение максимальных значений продольных напряжений в экране в зависимости от модуля деформации каменной наброски а – схема 1 (при отсутствии бетонной подготовки), б – схема 2 (при наличии бетонной подготовки)

Fig. 13. Changing the maximum values of longitudinal stresses in the face depending on the modulus of deformation of the rock blanket a - scheme 1 (in the absence of concrete blinding coat), b - scheme 2 (in the presence of concrete blinding coat)

4 Conclusions

• 1.    Уменьшение со временем модуля линейной деформации бетона E б , происходящее вследствие ползучести, оказывает существенное влияние на напряжённо-деформированное состояние выполненного из него экрана – оно ведёт к уменьшению воспринимаемым экраном сжимающих и растягивающих напряжений. Из-за того, что деформации каменной наброски формируются в течение довольного времени, высокие напряжения в экране могут быть снижены за счёт процессов релаксации. Таким образом, продолжительное восприятие плотиной внешних нагрузок способствует трещиностойкости экрана.

• 2.    Следует иметь в виду, благоприятное влияние эффекта релаксации напряжений в бетоне на напряженно-деформированное состояние экрана может проявиться только в том случае, если деформации грунта будут формироваться более длительно, чем деформации бетона. По-видимому, чаще происходит наоборот. По этой причине неблагоприятным является быстрое наполнение водохранилища, т.к. при этом напряжения в бетоне не смогут быть релаксированы. Рекомендуется осуществлять наполнение водохранилища постепенно.

• 3.    Вполне обоснованным является выполнение расчётов напряженно-деформированного состояния экрана при модуле линейной деформации бетона E б , соответствующем его начальному значению, т.к. этот случай соответствует более опасному. Кроме того, это обосновывается также тем, что изменения напряженно-деформированного состояния экрана, вносимые ползучестью, не столь значительны, как можно было бы ожидать: снижение модуля деформации бетона в 2,5 раза (на 60%) уменьшает растягивающие напряжения примерно на 30%.

• 4.    Ползучесть бетона с разной степенью эффективности сказывается на изгибающие моменты и продольные силы в экране. Ползучесть бетона в большей степени влияет на изгибающие моменты, а не на продольные силы. Мала степень влияния ползучести на моменты от продольного изгиба. Степень влияния ползучести на напряженно-деформированное состояние экрана зависит от схемы сопряжения экрана с телом плотины. Если трение между ними уменьшено, то степень влияния уменьшается.

• 5.    Учёт влияния ползучести позволяет уточнить рекомендации по выбору деформативных характеристик каменной наброски, обеспечивающих трещиностойкость бетонного экрана плотины высотой 100 м. При использовании мероприятий по снижению трения на контакте экрана и подэкрановой зоны модуль линейной деформации каменной наброски E к должен составлять не менее 140 МПа при коэффициенте Пуассона каменной наброски ν к =0,2 и не менее 330 МПа при ν к =0,3. Если не учитывать ползучесть бетона, то рекомендуемые значения E к должны быть увеличены в 2 раза.