Влияние ультразвука на процессы формирования и развития электрической искры при электроакустическом напылении

Введение. При нанесении износостойких покрытий методом электроакустического напыления образуется сравнительно узкий токопроводящий канал с высокой температурой и ионизацией, в котором выделяется джоулево тепло, что приводит к повышению давления и расширению канала. Расширяющийся канал действует подобно поршню на остальной газ и, так как расширение происходит со сверхзвуковой скоростью, вызывает в нем ударную волну, которая распространяется впереди этого своеобразного поршня. Температура в области ударной волны гораздо выше, чем в невозмущенном газе, а температура в самом канале во много раз больше, чем в ударной волне. Соответственно, плотность газа в канале очень мала, подавляющая часть массы движущегося газа вытесняется из него, что и дает возможность рассматривать границу канала как поршень [1].

Сам факт образования узкого канала можно понять так: при действии ультразвука, а также после пробоя газа и появления в нем проводимости в местах протекания тока выделяется джоулево тепло. Электропроводность газа, как известно, сильно возрастает с температурой. Так, при высокой степени ионизации, когда существенны столкновения электронов с ионами, электропроводность пропорциональна T 32 . При малой ионизации эта зависимость более резкая, т.к. с ростом T быстро возрастает степень ионизации и, следовательно, появляется тенденция к концентрации тока в сравнительно узком канале. В местах, где выше температура, проводимость тока больше, значит, там течёт больший ток и выделяется больше тепла. Это приводит к еще большему разогреву и так далее [2].

Физическими процессами, определяющими ширину канала и предел концентрации тока, является отвод тепла из канала и расширение нагретой области под действием давления. Каналом можно считать область до точки, где температура и степень ионизации существенно понижается. В канале можно пренебречь инерцией газа, но надо учесть выделение и перенос тепла. В области ударной волны нужно учитывать инерцию, но можно пренебречь электро- и теплопроводностью. Эти две области разделены переходным слоем — «оболочкой» канала. В оболочке происходит нагрев и ионизация входящего в канал газа [3, 4].

Материалы и методы. Основными уравнениями задачи являются уравнения непрерывности, движения и переноса энергии с учетом действия ультразвукового поля. Они имеют вид [5, 6]

^£ = v «E+p51rVl = о

• 5 t 5 r     r 5 r

( 5 V д V V V d p „ pl+ V | +    = 0

^5 t d r ) d r

5 (    p V ² V   1 5 f     (   p  V ² Vf  d ( rq )

= jE + U

l pE +      |+      <  r p V l Е + +     |^ +

5t ^      2 )  r 5 r [    ^   p   2 )f   r5 r где p — плотность, V — скорость, p — давление, 8 — внутренняя энергия на единицу массы газа, q — поток тепла, j — плотность тока, E — электрическое поле, U — вклад ультразвукового поля.

Уравнение состояния имеет вид

Р = ( n e ⁺ n i ) ^T = P ^T ( z ^{+ 1} )/ m a                                             ⁽⁴⁾

где m a — средняя масса атома; n e ,n i — числа электронов и ионов в единице объема; z средний заряд иона; n e =zn i . Температура выражена в энергетических единицах.

Машиностроение и машиноведение

Будем считать, что ионизацию в канале можно подсчитать по формуле Саха. Внутренняя энергия газа

3 p₊j_ ₌ p 3₊ I

• 2 p m_a   p 2 ( z + 1 ) T

где I — полная энергия ионизации плюс энергия диссоциации, отнесенная на один атом. Формулу (5) удобно применять в случае полной ионизации; при неполной ионизации с увеличением T возрастает и величина I. При этом, как следует из формулы Саха, I/T « const , поэтому для 8 более удобна формула

1 p                                                           (6)

Е =--

• Y- 1 р

где у — эффективный показатель адиабаты; для воздуха у =1,22.

Электропроводность О "и теплопроводность X сильно ионизированного газа равны _С = _{С 1} ( т ) т ³² = 3 ст' ( z ) T 32/ ( 4 e Ч2 П т ^ )

Х = Х 1 ( z ) T ^5/2

Здесь e, m — заряд и масса электрона, X = ln ( 3 Т ³²J ( ze³ ^ 4 п n e ) ) , С (z) — безразмерный коэффициент.

Для z=1 значение с =1,95. Величина х e ² /ст T , согласно закону Видемана-Франца, порядка 1. Для Я = 5 С

1(1)= 3,4 1013сек-1 eV^-3/2 ,

Х 1 (1)=3,9 1020 см-1 сек-1 eV⁵'².

Результаты исследования. Предположим, что зависимость от времени радиуса канала, граница кото-k рого играет роль поршня, вытесняющего газ, имеет вид a(t)=At ; движение в области ударной волны определяется двумя размерными параметрами A, р.

В уравнениях (4)–(6) введем безразмерные обозначения ( a c — радиус фронта волны)

x = rfac ( t), Р'( x ) = Р/Ро, V'(x ) = V/ac, P'(x )= plPo aC

Пренебрегая выделением и переносом тепла, запишем систему (1)–(3) в форме

( Vx ) dp ’ + p' — = 0 dx xdx

(1 -1) V' + (V'-x) — + - dp’ = 0

V k J              dx p’ dx

(л   1)              dp ‘

21 1 — I p + (V - x)--+ y p=

V   k J            dx xdx с граничными условиями при x=1

p' = (y+1)/(y-1), V' = 2/(y-1),p' = 2(y-1)

Положение поршня определяется точкой, где V=x. Давление на поршень pk можно выразить через ско- рость поршня.

p_k = K p P o ^{a 2} ,

где «коэффициент сопротивления» K «0,9 (K =p '(а)с?/с?) находится из численного решения системы (9). ppc

Будем пренебрегать излучением и примем, что dT q = -х dr

Пусть температура T в канале много больше, чем требуется для полной ионизации, следовательно, на краю Т много меньше, чем в центре. Положим Т=0 при r=a. Введем безразмерные обозначения r2

⁵ = С ²^ ? ) ^,

9 ( 5 ) = T , T ₀

1 r ( r V u =-- 1---

9 2 a V a  a

r

q 5 ( V r

—+d--- pa 2V a a

где Т 0 — температура на оси. Давление считаем постоянным по сечению канала.

Если отвод тепла из канала осуществляется «прозрачным излучателем», то для области канала можно

указать простое автомодельное решение: давление, температура и плотность постоянны по сечению, а скорость пропорциональна радиусу. Все падение температуры сосредоточено в оболочке. Там же поглощается излучение и происходит ионизация газа, поступающего в канал. Считая оболочку тонкой, можно получить систему уравнений для основных параметров канала. В общем случае можно пользоваться для оценок этими уравнениями как математической моделью, описывающей, хотя и грубо, основные процессы в канале. При этом приближен-

но учитываются действия ультразвука и теплопроводность [7].

Уравнения баланса энергии для канала и оболочки имеют вид

dW   d n a ²

--= p---- dt dt

= Qj+ Qu

,

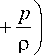
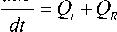
где M, W — масса и энергия газа в канале. Уравнение (15) получается интегрированием (3) по сечению канала (включая оболочку) без предположения о виде распределения величин по сечению. Для однородной модели положим

W = M • e , M = n • a ² p .

Уравнения (14), (15) есть следствие закона сохранения энергии. Выражения для выделения тепла Q j за счет электрического поля и тепла Q U за счет ультразвукового поля, а также для теплоотвода излучением Q R и теплопроводностью Q T можно взять в виде

Qj = j2 In a2 ст,   Qu  n^

Qr =n a2QR(p,T),   QT = 1,3 • 2nx T где to — частота ультразвуковых колебаний, n — размерный коэффициент.

Сравнивая (14) и (15), получим, что

Qt + Qr = Ц (Qj + Qu ) , где Ц — коэффициент порядка 1. Если Т не зависит от 1, то

Ц = У

2 2 Л-1

^{1 + (,} - 1 ) 2 a ² VOF )

- 1

Рассмотрим канал в воздухе с проводимостью ст =2^.1014 сек 1; Kp =0,9; у =1,2; j ~ 1 ; следовательно,

^ =4,5. Для радиуса канала получим выражение

• V, -и.      1

a = 0,93 ( 1 + О ) ^/б р ^/б j ^/3 1 ^{/2                                              (20)}

Здесь, а измеряется в мм, j в кА, 1 в мксек; р 0 =1,29^.10 ³ г/см3 при атмосферном давлении. Если же ударная волна слабая, то радиус аналогично находится из (19).

Ниже в таблице 1 приводятся значения радиуса, рассчитанные по формуле (20), при разных значениях О и 1 (мксек) при напряжении разряда V =30 В и емкости батареи c =0,15 мкФ, а также при индуктивности в цепи L =4 нГн (что отвечает j=V/L =7,5.10 А/сек).

Таблица 1

Радиус канала при различных значениях 9, 1

T О	0,3	0,5	1
0	0,65	1,00	1,62
1	0,73	1,12	1,82
2	0,78	1,20	1,95
3	0,82	1,26	2,04

Проведем оценки температуры в канале. Считаем, что Ц ~ 1, для того же разряда, что и выше в момент 1 =1 мксек при L =4 нГн имеем, что Q j + Q U = ( 1 + О ) 1,7 •Ю ¹³ эрг/см сек. Если считать, что все тепло переносится электронной     теплопроводностью,     а     излучением     пренебречь,     то     получим,     что

T ~ 4 ( 1 + О )eV . Приняв Т =4e V найдем, что количество ионов в единице объема в этом случае будет n j =9 10 , что по порядку соответствует экспериментальным значениям.

Заключение. На основании построенной приближенной модели можно сделать следующие выводы о влиянии ультразвука на развитие искрового канала.

• 1.    Радиус канала увеличивается в (1+ О )^^ раз по сравнению со случаем, когда нет ультразвука, где О — отношение энергий электрического и ультразвукового полей.

• 2.    Температура в канале увеличивается пропорционально (1+ О ) в предположении, что отток тепла осуществляется электронной теплопроводностью.

• 3.    Уже в момент образования ударной волны наступает почти полная ионизация в канале и могут создаваться условия для двукратной ионизации при высоких энергиях ультразвука.

  Машиностроение и машиноведение