Влияние управляющего параметра на режимы динамики модели Морана-Рикера с запаздыванием

п. Аякс 10, остров Русский, г. Владивосток, 690922, e-mail: ,

Массовые вспышки численности насекомых-вредителей могут приводить к массовой гибели древостоев, в этих ситуациях остро встает вопрос о регуляции и управлении численностью таких видов [3]. Именно поэтому исследования, направленные на изучение механизмов, вызывающих массовые размножения насекомых, и разработку стратегий управления такими популяциями, сохраняют свою актуальность [6]. Отметим, что существует множество методов регулирования численности вредных насекомых – от борьбы путем применения естественных врагов до обработки специализированными химическими средствами с помощью авиации [5, 8].

В рамках данной работы предлагается модель Морана-Рикера с управляющим параметром, позволяющая анализировать возможные сценарии развития популяции с учетом ежегодных мер, направленных на регуляцию ее численности.

Уравнения динамики

Модель Морана-Рикера с однолетним запаздыванием имеет вид:

x n+ 1 = axexp ^- 0 x_n-b X -1 ) , (1) где x_n – численность популяции, с которой она вступает в n -й период размножения, а – репродуктивный потенциал популяции. Множитель exp(– b 0 x n -b 1 x n -1 ) характеризует экологическое лимитирование роста численности популяции. Очевидно, что здесь в течение двух поколений – текущего и предыдущего – сказываются ограничения ресурсов жизнедеятельности. Параметр b ₁ характеризует степень уменьшения величины необходимых ресурсов, связанных с их потреблением предыдущим поколением. Уменьшение ресурсов может быть, в частности, интерпретировано как эквивалентное снижение репродуктивного потенциала текущего поколения. Параметр b ₀ характеризует интенсивность плотностно-зависимого экологического лимитирования в условиях ограничения ресурсов, приходящихся на одну особь популяции [2].

Дополнительно предполагается, что ежегодно проводят мероприятия, направленные на

снижение численности популяции, в результате которых гибнет пропорциональная общей численности доля особей. Тогда уравнение динамики (1) принимает вид:

x + 1 = ax n (^1- u ) ^exp^(-(1- u ) x n b 0 ^-b 1 ^(1- u ) x_n -1 ) , (2) где u – доля «изъятия» особей, пропорциональная общей численности. Очевидно, что 0≤ u ≤1. В этом контексте смысл параметра u является управляющим параметром и синонимичен «изъятию» некоторой доли от общей численности с целью поддержки численности популяции на низком или «безопасном» уровне.

Несложная замена переменных y _n=x_{n –1} и переход к новой системе координат b_ox_n ^ х_п , Ь о У п ^ У п сводит модель (1) к системе без запаздывания, имеющей вид:

, (3)

vn+1 %п

где р = Ьг/Ь0.

Параметр ρ в этом случае характеризует относительный «вклад» предыдущего поколения в экологическое плотностно-зависимое лимитирование воспроизводства популяции.

Результаты исследования

Проведено аналитическое и численное исследование модели (3). Показано, что модель (3) имеет две неподвижные точки: тривиальную, соответствующую гибели популяции, и нетривиальную. При этом равновесная численность немонотонно зависит от u : стационарная численность популяции может как увеличиваться, так и уменьшаться с ростом значений управляющего параметра. Продемонстрировано, что при скорости роста популяции больше е в модели возникает эффект

Гидры, когда увеличение интенсивности мер, направленных на снижение, сопровождается ростом численности в силу снижения внутривидовой конкуренции за ресурсы. Как следствие, важно, при каких условиях возникает эффект Гидры, чтобы «изъятием» не спровоцировать вспышку численности [4].

Построены параметрические портреты, соответствующие областям устойчивости модели Морана-Рикера с управляющим параметром (3), позволяющие заключить, что рост u ведет к монотонному расширению областей устойчивости обеих неподвижных точек (рис. 1).

Анализ на устойчивость проводился на основе собственных чисел характеристического многочлена F( А ) = А² + p A + q = 0 матрицы Якоби, построенной для модели (3) [1]. Если А = 1 , то F (1) = 0 соответствует линии транскритической бифуркации (T); А = - 1 , то это линия бифуркации удвоения периода (PD); q = 1 , то линия бифуркации Неймарка-Сакера (NS). Найденные границы области устойчивости определяются следующими соотношениями: T: , PD: , NS:

и представлены на рис. 1.

Проведенный анализ на устойчивость показал, что сценарий потери устойчивости (характер возникающих колебаний) определяется параметром, характеризующим экологическое лимитирование. При р <  1/3 потеря устойчивости может произойти только при переходе одного из

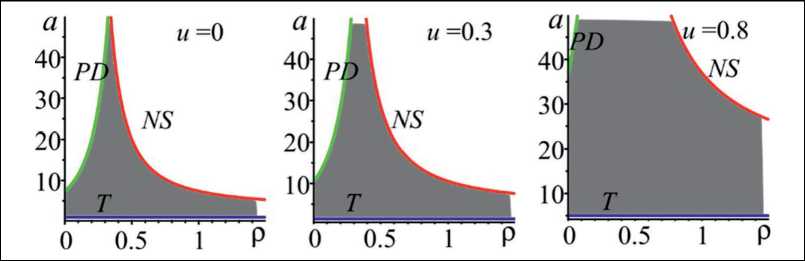
Рис. 1. Область устойчивости нетривиального равновесия (2) при вариации значений параметра u. T, PD, NS – линии, соответствующие транскритической бифуркации, бифуркации удвоения периода и Неймарка-Сакера бифуркации соответственно

Fig. 1. Stability domain of the nontrivial equilibrium (2) with variations in the parameter u values. T, PD, NS are the lines corresponding to the transcritical bifurcation, the period-doubling bifurcation and the Neimark-Sacker bifurcation, respectively собственных чисел через -1 и сопровождается рождением предельного 2-цикла. При р > 1/3 потеря устойчивости может произойти только при комплексно-сопряженных корнях характеристического уравнения, при переходе |л| через 1, и сопровождается появлением предельных инвариантных кривых. Здесь рост значений параметра ρ приводит к быстрому сужению диапазона устойчивости, т.е. возникновение сложно организованных колебаний численности происходит при более низких значениях репродуктивного потенциала. Следовательно, как только вклад предыдущего поколения в лимитирование воспроизводства популяции начинает превосходить вклад текущего поколения, так при все более низких значениях репродуктивного потенциала возникают колебания численности. В целом можно отметить, что зависимость популяционной динамики от скорости восстановления ресурсов, необходимых для жизнедеятельности вида, приводит к тому, что популяция в большинстве случаев демонстрирует квазипериодическую динамику.

Рост значений коэффициента u расширяет область параметрического пространства, в которой динамика системы стремится к устойчивому равновесию. Действительно, с увеличением u граница области устойчивости нетривиального равновесия, соответствующая потере устойчивости по сценарию Неймарка-Сакера, сдвигается вверх вдоль оси ординат и тем самым расширяет исходную область устойчивости. При этом потеря устойчивости через нее происходит при более высоких значениях репродуктивного потенциала. С другой стороны, при увеличении интенсивности изъятия линия бифуркации удвоение периода также смещается в направлении, ведущем к увеличению исходного размера области устойчивости. Таким образом, возникновение периодических колебаний становится возможным при более высоких значениях скорости роста популяции (рис. 1).

Анализ вида областей устойчивости системы, представленных на рис. 1, позволяет заключить, что при фиксированных значениях демографических параметров, когда свободно развивающаяся популяция демонстрирует нерегулярную динамику, введение управления и последовательное увеличение доли изъятия может привести к стабилизации, а затем к вырождению. При этом двухгодичные колебания возможны в достаточно узком диапазоне значений демографических параметров, и, как правило, реализуются, когда ограничение роста численности осущест- вляется преимущественно через плотностно-зависимую регуляцию в текущем году.

Таким образом, показано, что изъятие расширяет область устойчивости нетривиального равновесия, то есть меры, направленные на снижение численности популяции, в перспективе могут стабилизировать динамику. Однако вариация численности популяции или изменяющаяся интенсивность «изъятия» при значениях популяционных параметров из области мультистабильности могут привести к смене наблюдаемого режима динамики за счет смещения текущей численности в бассейн притяжения альтернативного режима динамики. Это связано с тем, что в системе наблюдается явление мультирежимности: при одинаковых значениях демографических параметров популяция может демонстрировать разные типы динамики – стабильную, периодическую или нерегулярную.

В работе [7] модель Морана-Рикера (1) была применена к описанию динамики плотности популяции листовертки лиственничной (Zeiraphera diniana Gn.). Найденной Л.В. Недорезовым и Д.Л. Садыковой [7] оценке значений параметров соответствует асимптотический режим, близкий к циклу длины 9, что хорошо согласуется с результатами наблюдений [7]. На рис. 2а приведены результаты описания динамики плотности Zeiraphera griseana, полученные в работе [7]. Как видно, модельная траектория хорошо описывает реальные данные, улавливая ключевые пики. В рамках настоящего исследования на основе точечной оценки мы анализируем влияние управляющего параметра на возможные сценарии развития популяции. Для этого были построены модельные траектории при различных значениях коэффициента u , сопоставление которых с реальной динамикой популяции листовертки лиственничной представлено на рис. 2.

Как видно, ежегодные мероприятия, направленные на снижение численности популяции, в перспективе ведут к уменьшению периода колебаний, при этом вспышки численности сохраняются и происходят раньше, чем ожидалось (рис. 2b). При этом увеличение интенсивности «изъятия» уменьшает амплитуду колебаний, и как результат вспышки численности популяции наблюдаются чаще, но с меньшим размахом (рис. 2d). С другой стороны, значения коэффициентов, полученные Л.В. Недорезовым и Д.Л. Садыковой, располагаются в параметрической области, соответствующей ситуации, когда рост «изъятия» сопровождается ростом стационарной численности,

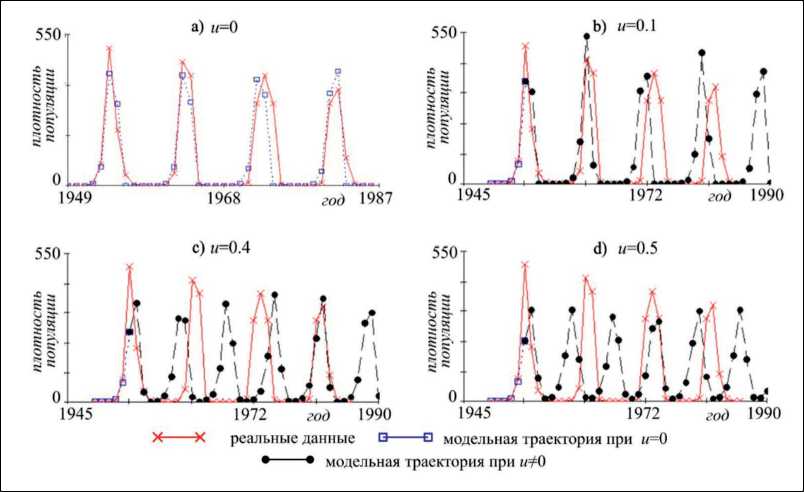
Рис. 2. Результаты описания динамики плотности листовертки лиственничной моделью Морана-Рикера с лагом 1 при вариации значений управляющего параметра. u=0 соответствует модельной траектории, построенной по оценке параметров, полученной Л.В. Недорезовым и Д.Л. Садыковой [5]

Fig. 2. Results of the larch leaf roller density dynamics description by the Moran-Ricker model, with a lag of 1, with variations in the control parameter values. u=0 corresponds to the model trajectory, constructed on estimation of the parameters made by L.V. Nedorezov and D.L. Sadykova [5]

то есть возникает эффект Гидры. Следовательно, пороговое значение управляющего параметра, переход через которое будет вести к снижению стационарной численности, составляет 0.67. В свою очередь бифуркационное значение параметра u , при котором происходит «схлопывание» инвариантной кривой и переход к стабильной динамике, составляет 0.63. Таким образом, по результатам модельного анализа стабилизация динамики видов, демографические характеристики которых близки к листовертке лиственничной (Zeiraphera griseana), будет наблюдаться при ежегодной обработке территории, составляющей более 63%, а снижение стационарной численности – при ежегодной обработке более 67% территории.