Влияние уровня сформированности регулятивных УУД на развитие личности младшего школьника

Схематично регулятивные универсальные учебные действия можно представить так:

Ряулятжжные ушиерсмьяые ученые дейпнн

Подчеркнем, что важнейшее качество универсального действия – операциональность – представленность последовательных логических операций (шагов), совокупность которых составляет сущность данного учебного действия и отражает его специфичность, отличие от других учебных действий [1, с. 22]. Понять, как нужно построить процесс учебного взаимодействия можно только тогда, когда каждое учебное действие будет представлено в виде операций, необходимых для успешного его осуществления с целью решения учебной задачи.

Рассмотрим регулятивное универсальное учебное действие «планирование выполнения учебной задачи». Оно состоит из следующих операций: постановка цели предстоящей деятельности как ее результата; продумывание «шагов», с помощью которых можно получить результат; выстраивание последовательности выбранных «шагов»; отражение последовательности решения учебной задачи в выбранном словесном или графическом виде; высказывание предположения о том, какие операции наиболее целесообразны для решения учебной задачи.

На первых этапах обучения в начальной школе для учащихся характерно отсутствие действия планирования как целостной единицы деятельности. Ученик способен выполнять отдельные операции, внутренне не связывая их друг с другом. О становлении планирования как универсального учебного действия можно говорить в том случае, если ученик умеет самостоятельно осуществлять построение плана поиска решения задачи, а затем перестраивает его и предлагает другой план решения этой же задачи; использует знание общих принципов построения плана, выстраивает конкретную, необхо- димую для решения данной задачи последовательность действий. На протяжении всего процесса решения задачи ученик работает самостоятельно и допущенные ошибки исправляет сам.

Для становления регулятивного универсального учебного действия «планирование выполнения учебной задачи» необходимо задействовать возможности содержания обучения математике, которое требует определения последовательности предстоящих шагов в «учебных алгоритмах». Формирование этих операций напрямую связано с достижением предметных результатов освоения основной образовательной программы, зафиксированных в ФГОС начального общего образования: «овладение основами алгоритмического мышления, записи и выполнения алгоритмов; умение действовать в соответствии с алгоритмом и строить простейшие алгоритмы» [5, с. 11–12]. Это правила порядка выполнения действий в числовых выражениях; сравнение чисел в пределах 1 000 000; устное выполнение арифметических действий в пределах сотни и с большими числами в случаях, легко сводимых к действиям в пределах ста; письменные вычисления (сложение и вычитание многозначных чисел, умножение и деление многозначных чисел на однозначное и двузначное число); решение текстовых задач; вычерчивание с помощью линейки отрезок заданной длины; вычисление периметра и площади прямоугольника (квадрата) и др.

Например: учащимся 4-го класса сначала предлагается не только решить задачу, действуя по данному плану, но и « записать другой план решения этой задачи »: «Периметр квадрата равен 20 см. Из четырех таких квадратов составили большой квадрат. Найди его площадь. Действуй по плану: 1. Нарисуй чертеж. 2. Найди длину стороны маленького квадрата. 3. Найди длину стороны большого квадрата. 4. Найди площадь большого квадрата.

На определенном этапе ученики самостоятельно приступают к заданиям, связанным с выполнением действий по уже освоенному алгоритму, могут участвовать в уточнении условий и способов работы, готовы выбирать и объяснять «шаги», которые будут наиболее целесообразными (удачными, рациональными) для выполнения задания.

Например: на уроке математики в 1-м классе учитель предлагает по схеме в учебнике рассказать, как к 9 можно прибавить 2.

Объясни, как сложить 9 и 2 разными способами.

1) I 2)       3) "©^ Ю

1    1   9 + 1 + 1 = 1 t

Учащиеся объясняют, что они могут получить результат сложения используя фишки (1), линейку (2); определяют, что эти «шаги» приводят к получению верного результата, но занимают много времени. После этого рассматривают третий вариант: прибавление по частям и приходят к выводу, что он более рациональный:

1.Представлю число 2 в виде суммы удобных слагаемых: это 1 + 1

• 2.    К числу 9 сначала прибавлю 1, чтобы получить 10.

• 3.    К результату прибавлю единицу. Получаю ответ: число 11.

Далее учитель просит объяснить, какие «шаги» можно считать наиболее целесообразными, если надо выполнить сложение: 8 + 3; 7 + 4, 9 + 5?

Позднее можно наблюдать уверенные самостоятельные действия ученика не только в выстраивании последовательности действий для решения стандартных задач, но и требующие «перестройки» последовательности шагов, после обнаружения некоторой новизны (нестандартности) в предъявленной задаче.

Первым универсальным действием, связанным с прогнозированием, является определение возможности выполнения учебной задачи. Пооперационный состав этого действия следующий: анализ предъявленной учебной задачи; высказывание предположения, (вывода) для себя о возможности ус- пешного решения поставленной задачи; соотнесение (сравнение) собственных возможностей с теми, которые необходимы (требуются) для выполнения; ответ самому себе на вопрос о возможности решения данной учебной задачи; определение, что необходимо сделать, чтобы появилась возможность успешной деятельности.

Очень важно организовать этап предварительного (контрольного) прогноза. Цель его: учить детей предсказывать результат деятельности, представлять способ решения задачи, предвидеть трудности. В процессе учебного диалога высказываются предположения о возможных результатах деятельности; осуществляется анализ набора предполагаемых операций

Учитель предлагает прочитать математическую задачу, в которой отсутствует условие, позволяющее ее решить. Учащиеся, еще не приступая к работе по решению задачи, обсуждают возможность получения результата (строят прогноз): можно ли дать ответ на вопрос задачи? Почему?

Анализ подобных ситуаций позволяет подвести детей к осознанному выводу: перед тем, как приступить к решению учебной задачи, нужно «прикинуть» (предположить, быстро представить), достаточно ли условий для ее выполнения, все ли условия верны, какие из них не нужны, а каких не хватает и т.п.

Рассмотрим еще пример задания, в котором требуется еще до начала работы: подумать, сделать «прикидку», спрогнозировать варианты ответов: «Выскажите предположение о том, каким образом можно распределить записи 7 + 2, 12 – 3, 5 + 3, 10 – 2 по группам двумя разными способами.»Ученик строит прогноз, определяет, по какому существенному признаку он может произвести группировку: выделение действий сложения (7 + 2, 5 + 3) и вычитания (12 – 3, 10 – 2)или записей с результатом 9 (7 + 2, 12 – 3) и результатом 8 (5 + 3, 10 – 2).

Одним из универсальных учебных действий, связанных с контролем, является контроль конечного результата собственной/чужой деятельности и его корректировка. Пооперационный состав этого действия такой: «проверяю полученный результат: сопоставляю (сравниваю) с правильным ответом; выявляю (вижу) допущенную ошибку (свою и/или чужую); устанавливаю (объясняю) причину ошибки; исправляю ошибку; делаю вывод, как избежать такой ошибки в будущем»[1, c. 97]. Подчеркнем, что речь идет о контроле как своего результата, так и чужого результата. Для отработки данной операции важно постоянно предлагать проверять как свою работу, так и работу соседа по парте, работу ученика «другого» класса. Со временем эта операция проходит уже не только как прямое сравнение своей работы с правильно выполненной, но и как проверка собственной работы через определенные «подсказки», «ключи» к проверке», задания вида «Проверь себя».

Например. Впиши пропущенные цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9. Если сомневаешься, запиши их сначала карандашом.

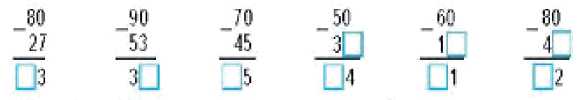
Проверь себя: каждая цифра должна быть записана один раз.

***

Важнейшее значение развитой рефлексивности, сформированности регулятивных действий в том, что они оказывают положительное влияние на развитие всех психических процессов. По отношению к мышлению это констатировал С.Л. Рубинштейн: «Мышление соотносит, сопоставляет каждую деталь, возникающую в процессе мышления, с задачей, на разрешение которой направлен мыслительный процесс, и ее условиями. Совершающаяся таким образом проверка, критика, контроль характеризуют мышление как сознательный процесс» [3, c. 370].

Таким образом, любое учебное действие, если оно протекает сознательно, регулируется его исполнителем – планируется, контролируется, корректируется, оценивается. Способность к регулятивной деятельности «позволяет говорить о человеке как о саморегулирующейся, самообучающейся, самосовершенствующейся системе»[4, c. 246]. В теории учебной деятельности (Д.Б. Эльконин и др.) контроль и самоконтроль, оценка и самооценка рассматриваются как существенные компоненты учебной деятельности. Эти положения в свою очередь стали предпосылкой внесения этих психических феноменов в планируемые результаты обучения ФГОС НОО.

Своевременно оценить успешность формирования регулятивных УУД позволяет разработанная в рамках системы учебников «Начальная школа ХХI века» педагогическая диагностика[1].Она проводится в процессе всего периода обучения младшего школьника. Выполнение заданий педагогической диагностики требует от учащихся понимания смысла нестандартного задания, умения отбирать необходимые способы действия, выполняя при этом мыслительные операции анализа, синтеза, сравнения, обобщения. Проведение такой контролирующей деятельности становится существенным показателем стратегии обучения, характеризующей направленность учителя на достижение требований стандарта.

Высокий уровень выполнения диагностических заданий учащимися с 1 по 4 класс свидетельствует о качестве сформированности регулятивных универсальных учебных действий. Это подтверждается рубрикой «Характеристика выполнения задания»[3], которая содержит качественную, содержательную «оценку», дополнительно к той количественной оценке, которую учитель выставляет за каждое диагностическое задание (0, 1, 2, 3 балла). В рубрике «Характеристика выполнения задания» уточняется: успешное выполнение каких регулятивных действий позволило ученику получить высокий результат. Экспериментальные исследования показали, что к началу 4 класса уровень сформированнос-ти регулятивных универсальных учебных действий у младших школьников составляет 77% (в школах, работающих по системе учебников «Начальная школа ХХI»).

Таким образом, точное понимание педагогом операционального состава отдельного регулятивного универсального действия позволяет создавать педагогические условия для успешного его формирования у младшего школьника, а применение технологии «педагогическая диагностика» – отслеживать качество и динамику формирования этих учебных действи