Влияние условий измерения и квантования на информативные параметры эхо-сигнала дождя

Известно [см. 1-3], что данные о физических свойствах дождевых капель: K w - наведенном дипольном моменте капли, l ( r₀,K w , R ) - затухании при распространении сигнала вдоль сферической координаты дальности, а также данные о физических свойствах облачно-дождевых систем: R - интенсивности дождя и M - водности облачно-дождевой системы лежат в основе физико-математических моделей ориентированных на решения трех групп задач: радиофизические, задачи обработки сигналов и электрохимические.

Это следующие задачи: исследование загрязнения воздушной среды, построение зон радио покрытия сотовой связи в осадках и зон ослабления сигнала при радиорелейной связи, построение карт солености (и/или загрязнений акваторий, или воздушного бассейна), обнаружения патогенных ионов в каплях дождя, измерение водности облачно-дождевых систем с целью предотвращения возгорания двигателей реактивных самолетов, измерение водности M при принудительном поливе сельскохозяйственных угодий в засушливые годы из кучевых облаков, построении метеорологических карт.

Формулировка радиофизической модели формирования сигнала метеоэхо

Алгоритм селекции физических свойств капель дождя и физических свойств облачно дождевых систем изложен в [1, 2]. В [1] доказано, а в [2] обосновано, что эхо-сигнал от однород- Вестник ЮУрГУ. Серия «Математика. Механика. Физика»

2020, том 12, № 1, С. 63–72                                                                          ⁶³

Физика ных и изотропных импульсных объемов дождя есть центрированный двумерный нормальный вектор. Этот вектор является информативным относительно Kw, l(r0,Kw,R), R и M . Комплексная диэлектрическая проницаемость ё (to) (см. [2]) связана с комплексным относительным показателем преломления и с наведенным дипольным моментом капли Kw (см. [2, 3]) так:

(m 2 (to)-1)

Kw = (m2 (to) + 2) ’ где

m (to) = n (to)- jk (to) = £ (to) ц = (£(to) + i^to)) ц комплексный относительный показатель преломления; ё(to) = £(to) + i£"(to) - относительная комплексная диэлектрическая проницаемость капель дождя; µ – относительная магнитная проницаемость воды ц = 1 (0,999991) (см. [4]);

– коэффициент поглощения;

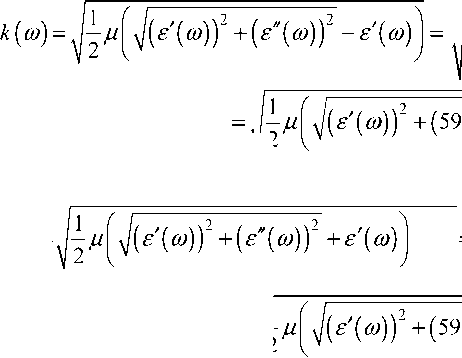
2Ц J(£'(to))2 +

V

V 2п£0 c 7

;

= 1 Ц (£,(to))2 +

^г 1

V 2п£0 c 7

\

- действительный показатель преломления; £ - вещественная часть комплексной диэлектрической проницаемости; £" - мнимая часть комплексной диэлектрической проницаемости; о -удельная проводимость среды распространения (капли воды); λ – длина волны зондирующего сигнала; to - круговая частота зондирующего сигнала; c = 1/^ £ ₀ Ц ₀ — скорость света в вакууме; £ ₀ - электрическая постоянная (электрическая (диэлектрическая) проницаемость вакуума); ц ₀ -магнитная постоянная (магнитная проницаемость вакуума).

Многократно зондируя на каждой из рабочих частот (см. [2]) и каждый раз (по результатам четырех зондирований) численно решая систему из трех уравнений (5), каждое из которых получается для текущего зондирования, получаем выборочные значения K w , l ( r ₀, K w , R ) и R . На основе выборочных значений K_w получаем прямоугольные матрицы выборок K_w . Затем, из выборок K_w , формируем матрицы оценок K ˆ _w . И, наконец, используя формулы (1)–(4) и уточненные формулы Дебая (см. [5, 6]), связывающие между собой величины: комплексную диэлектрическую проницаемость, T – температуру окружающей среды σ, ω и учитывающие зависимость σ и ε от T и ω , формируем матрицы оценок σ ˆ и ε ˆ ' . Заметим при этом, что физические величины K_w и R не зависят от давления в диапазоне возможных значений атмосферного давления на трассе распространения радиосигнала (см.[2, 3]).

Связь мощности эхосигнала P ( r ₀ ) и K w (см. [3]) имеет вид:

P (ro )=

P u g ² £ l ² ( r„ K w , R ) n ( r > , K w , R )

(4 П )³ r 02

2   п 2п j W (r, r0 )| dr J j f4 (0,ф) sin0 d0 dф =

r

= P^ug ^Х l , ⁽ r ⁰’ K w , R ) ^ 3 K_w I² N Л ^{- 7} / (7, Л D_max )- ^ 1— [cth( aF T ) - 1/( aF T )] —

2 6 r ₀²         Я ² w ^{0 maxV}8ln2             '        2

= Al ² | K w|² N о ( a R ^{- e} ) ^- 7 y ( 7, aR" ^e D max ) .                            (3)

В (5) приняты следующие обозначения. Р (r0) - мощность эхо-сигнала отраженного от дождево- го импульсного объема.

п=П51 KJ2 Z л

удельная эффективная площадь рассеяния.

Z = ~V ^Di — отражаемость разрешаемого импульсного объема АV (см. [2]), Di - диаметр капли, А V - величина импульсного объема на удалении r0, r0 - значение наклонной дальности (сферической координаты) до центра импульсного объема А V, Ри - мощность, излучаемая передатчиком, g2 – коэффициент усиления датчика (антенны) одновременно на прием и передачу,

W ( r , r ) = 2 { erf [ (2 aF 1c )( r - r + T 4) ] - erf [ (2 aF/c )( r - r - T 4) ] } ;

– вид весовой функции по дальности. r – значение текущей сферической координаты;

a = — ^= (6) 2 ln2

– первый коэффициент формирования амплитудно-частотной характеристики (АЧХ) согласованного фильтра приемника, F – ширина полосы пропускания приемника по уровню половинной мощности, τ – длительность зондирующего импульса, R – интенсивность осадков мм/час. При использовании распределения капель по размерам Маршала-Пальмера N ( D ) = N ₀ e ^{-Л D} , (см. [7]), уточняющих коэффициентов Литвинова и Циркунова и результатов из [8], имеет место выражение для уточненной отражаемости дождя Z = N ₀ Л ^{- 7} / ( 7, d ) (параметры N ₀ и Л входящие в формулу, описывающую распределение капель по размерам). При этом, при метеорологических измерениях используют следующие пары параметров N ₀ и Л : Л = a R ^e = 3,7 • R ^{- 0,37} мм ¹, N ₀ = 5,5 • 10³ мм ¹ - для осадков в течение первых 15 мин выпадения днём (см. [8]), Л = 4,3 • R ^{- 0,23} мм ^{- 1}, N ₀ = L10⁴ мм ¹ - для осадков спустя 30 мин после начала их выпадения днем (см. [9, 10]) и Л = 4,6 • R ^{- 0,23} мм^-1, N ₀ = 1,4 •Ю⁴ мм ^{- 1} - для ночных осадков (см.

[8, 9]). /(7,d) - неполная гамма функция (см. [10]), d = ЛDmax и Dmax - максимальный диаметр капли (Dmax = 6,5 мм (см. [3])).

1 = exp

( r,            )

-J(kg + k ) dr

k 0            J

= exp

( r,.

-J (( kg H2O k 0

⁺ k g O₂ ) ⁺ ( k d ⁺ k c ) ) dr

– потери в одну сторону за счет ослабления в атмосферных газах, в дожде и на каплях. kg = (kgH2O + kgO2) - коэффициент равный сумме коэффициентов затухания в атмосферном кислороде и парах воды. k = (kd + kc) - коэффициент ослабления в дожде и на каплях облаков. Поскольку kc и kd зависят от неизвестных Kw , R, M, а также от температуры среды, сезонного вида осадков и времени суток, то и величина l(r0,Кш,R) формально является неизвестным в выражении (5) так как зависит от неизвестных физических величин.

7/ /     х\2      7 2, х L- ( a , F , t ) c t

J (W(r, r0 )) dr = J l0fw (r0 - r)dr =------5------

0                  0                          2

- результат вычисление внешнего интеграла выражения, 1 ₀ = erf ( b ) - коэффициент при весовой функции f W2 ( r ₀ - r ) , который нормирует ее максимальное значение к единице,

Физика lr(a,F,T) = [cth(aFT) -1/(aFT)] - коэффициент потерь в приемнике обусловленный ограниченной полосой пропускания fw (ro- r ) = 2 Jf. (b) (erf (x+b)-erf (x - b));

– нормированная АЧХ приемника b = Fn] 4lnV2;(9)

– второй коэффициент формирования формы АЧХ приемника x = (2aFc)(r0 -r) ;(10)

– формальная переменная функции (8).

Аналитическое решение lr (a,F,T) получается при известной аппроксимации функции erf (У) функцией th(y). Аппроксимация учитывает реальные значения величин (9)-(10) и вы- полняется с большой точностью (см. [2]).

99^

8ln2 ^.

J J f ⁴( 9 , ^ )sin( 9 ) d 9 d o =

– значение внутреннего интеграла выражения (5) (см. [3]). Вычисление внутреннего интеграла (5) выполнено при предположении, что функция f (9,ф) - есть осесимметричная кривая гауссовско го вида. 91 - угловая ширина (в радианах) однократно используемой (либо на прием, либо на передачу) диаграммы направленности антенны (или датчика); ф -азимут; 9 - угол места.

Объединим по общим признакам все параметры формулы (5) в три группы. Первая группа

(образует множитель A =

P u g ² п 3 _ 9^ 2 6 r ₀ ² Я ² 8ln2

cth( aFT)--— aFT

C T

в (5)) и объединяет априорно извест-

ные конструктивные параметры измерительной системы (постоянные параметры фиксированные для каждого текущего зондирования). Вторая группа образует вектор В = ( N₀, а , в) априорно известных параметров дождя, координаты которого определены выше. Третья группа это неизвестные и статистически оцениваемые величины l ( r ₀, K w , R ) , K w и R.

Заметим, что неизвестные параметры l (r0, Kw, R), Kw и R можно грубо оценить по трем зондированиям (P1 (r0),P2 (r0), (r0)), численно решая систему из трех уравнений (5). Для n зондирований каждой из m частот строится матрица статистической выборки ||P(r0 )|| необходимая

ˆ

ˆ  ˆˆ

для расчета оценок l (r^, Kw, R), Kw, R, M , а затем и оценок <7 и £ по формулам (1)-(4) и уточненным эмпирическим формулам Дебая (см. [5, 6]). Меняя частоты зондирования в окрестности частоты f = 2,99792 ГГц (Я = 10 см, где Kw лежит в окрестности точки 0,9286 при t = 20 °C) и f = 48,353622 ГГц (Я = 0,62 см , где Kw лежит в окрестности точки 0,8926 при t = 20 °C) формируем матрицы σˆ и εˆ по уточненным эмпирическим формулам Дебая (см. [5, 6]). Эти матрицы нужны для решения радиофизических и электрохимических задач. Заметим, что информацию о физических свойствах дождевых капель несет Kw , а информацию о свойствах облачно-дождевой системы l(r0,Kw,M), R, M . При этом, |Kw|2 изменяется всего в пределах от 0,8312 до 0,9340 [3] для длин волн в диапазоне от 0,06 м до 0,10 м в диапазоне температур от 0 до 20 °C. Тогда очевидно, что смещение оценки величины P(r0), вызываемое как процессом формирования эхо-сигнала (тепловой шум приемника также искажает оценку P(r0)), так и квантова- нием, недопустимо. Для ледяных сфер Kw 2 составляет около 0,18 [3] и не зависит ни от температуры, ни от длины волны. Поэтому зимой затруднено измерение физических свойств атмосферной влаги.

Алгоритмы формирования состоятельных и несмещенных оценок первого и второго начальных моментов эхо-сигнала дождя

Окончательный вид вектора второго начального момента эхо-сигнала дождя будет иметь вид:

P = ( P ( Г о ) , P ( r + с т ) ) = P - ,                              (11)

где τ – шаг дискретизации при выборке сигнала или интервал времени между соседними выбо- рочными отсчетами данных; c – скорость света.

Напомним, что первое и второе предложение раздела Формулировка радиофизической задачи имеет следующий вид: в [1] доказано, а в [2] обосновано, что эхо-сигнал от однородных и изотропных импульсных объемов дождя есть центрированный двумерный нормальный вектор. Этот случайный вектор является информативным относительно K w , l ( r ₀, K w , R ) , R и M .

Действительно каждый элементарный отражатель – капля дождя находится на случайном расстоянии от излучателя и случайным образом ориентирована относительно плоского фронта падающей электромагнитной волны. Капли дождя приобретают скорость в поле тяготения земли. Форма капли при этом будет отличаться от сферической формы. Причина отклонения от сферической формы в том, что на движущиеся капли действуют: сопротивления воздуха, ветер и столкновения капель (см. [2]). Кроме того, капли имеют различные размеры. Поэтому эхо-сигнал от каждой капли будет иметь случайную фазу, распределенную в интервале от [0, 2π].

Таким образом, цитируя фразу из [2] запишем. Теперь мы можем применить центральную предельную теорему к действительной и мнимой частям сигнала. Теорема устанавливает, что распределение суммы независимых случайных величин стремится к нормальному закону при условии, что число слагаемых велико и ни одно из них не выделяется по величине в сравнении с остальными. Очевидно, что оба эти условия справедливы для гидрометеоров (дождевых капель), откуда следует, что синфазная и квадратурная составляющая распределены по нормальному закону с нулевым средним.

Поэтому на входе приемника происходит сложение двух векторов в каждой из квадратур комплексного сигнала: вектора сигнала эхо-сигнала дождя ξ и вектора сигнала теплового шума приемника n . Тогда обрабатывается вектор сигнала η = ξ + n , который пройдя частотноизбирательные цепи (что учтено в (5)), поступает на аналого-цифровой преобразователь, где подвергается дискретизации по времени и квантованию по уровню.

В итоге получается суммарный вектор δ = ξ + n + ζ , из которого и надлежит выделить ин- формативную составляющую вектор ξ .

Поскольку тепловой шум и эхо-сигнал дождя имеют различную природу, то координаты векторов ξ и n не коррелированы. С другой стороны вектор ζ статистически связан с вектором,

η = ξ + n так как получается из него с помощью нелинейного преобразования. В этом случае, следуя теореме дисперсий [12, 13]:

n

D X X i

V i = 1     )

n

= X D (Xi) + 2X Kj

i = 1                  i <  j

И, переходя к системе обозначений данной статьи, можем записать:

D g = ^D - + D n + D ? + ^{2 K} ZS + ² K zn •

Видим, что из выражения (13) следует следующее очевидное соотношение, позволяющее вычислить искомую информативную физическую величину P _ξ = D _ξ :

P - = D - = D g — D n — D ? - 2 K z- "  2 ^K ? n = D g — D n — D ? — 2 ^n '          (14)

В работе [14] получено выражение для вектора второго начального момента шума квантова- ния Dζ :

n \ fA2 A2 v(-1)n Г2n ) A2 A2 v(-1)n Г2n ))

D? = ( D?1,D? 2 )= 77+7^2 X 77T q cos I nrnin! I; 77+772 X —r q cos I 77nm 21 •(15)

V 12 (n) n=1 (n) V A ) 12 (n) n=1 (n) V A ))

Физика

Второе слагаемое в формуле (15), как следует из (14), приводит к смещению оценки вектора ˆˆ

P _ξ = D _ξ при выполнении оценки даже по выборочному алгоритму оценки второго центрального момента (учитывая предварительно вычисленные оценки m ˆ₁ и m ˆ₂ первого момента, выполненные по выборочному алгоритму первых моментов).

Рассмотрим результат (10) с учетом формулировки радиофизической задачи. Известно, что реальное значение проводимости дождевых капель σ достаточно мало. Например (см. [15, 16]), о = 0,38 • 10 ^{- 5} см •м^-1 для тщательно очищенной воды, о = 5 • 10 ^{- 4} - 100 • 10 ⁴ см •м^-1 - для дождевой воды и линейно зависит от ее минерализации (см. [16]) (т. е. от загрязнения атмосферной влаги промышленными выбросами). Сначала из численного решения уравнений вида (5), учитывая априорно известный вектор В = ( N ₀, а , в} и коэффициент A , получается выборочное значение K w . Затем, по ансамблю выборочных значений K w строится матрица оценок K w ( ^ )|| . И, наконец, по формулам (1)–(4) и уточненным формулам Дебая (см. [5, 6]),получаем оценки ε ˆ и σ ˆ для решения указанных во введении радиофизических и электрохимических задач.

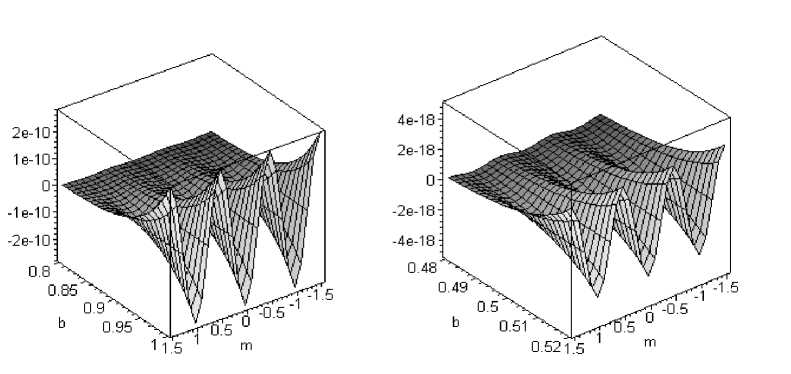
Информацию о K w несет мощность принятого сигнала P ( r₀ ) . Но, P ( r ₀ ) прямо пропорциональна о ^2 (с точностью до коэффициента А из (5)). Поэтому при т 1 * 0 и m 2 ^ 0, как следует из (14), появляется смещение вектора D _δ принимаемых сигналов на основании теоремы сложения дисперсий, которое зависит от вторых слагаемых в формуле (14). Тогда, если не применить алгоритм (14), то оценки ε ˆ и σ ˆ также становятся смещенными и несостоятельными. На рис. изображено второе слагаемое в формуле (15), которое есть функция β и m_j .

а )

б )

Зависимости второго слагаемого в выражениях D = (D1,D2) как функции в = А2/аП , (в = b) и mj для формулы (14) при А = 1 (отражающие доминанты есть).

На рисунке: а - зависимость получена при в = 0,8 - 1, б - при в = 0,48 - 0,52.

Основные выводы ˆ

Оценки D ^ г = 1, 2,..., n формируются из выборок мощности P ( r ₀ i ) , г = 1, 2,..., n (5). Где n – количество анализируемых сканов при фиксированной длительности импульса и длине волны зондирующего импульса при секторном сканировании. Квадрат амплитуды эхо-сигнала от капельной структуры, центр импульсного объема которой расположен на удалении r _{0 j} , имеет вид:

P ( Г /)

x, = -^ i ² , i = 1,2... N .                                 (16)

i A

Из [12] известно, что оценки первого и второго центрального момента формируются в виде выборочных алгоритмов:

1n mj=-L(sgn(Vxj )hlxy,j = n i=1

1,2;

2' 1 ^{n                                  2}

Dn. = ^n = _L Ksgn(Ту)) 4xymj) , j =1,2, j n где sgn

(xi)

– алгоритм определения знака амплитуды эхо-сигнала;

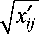
– модуль амплитуды

эхо-сигнала.

Возвращаясь к формулировке четвертого абзаца предыдущего раздела и учитывая строгое доказательство центрированности случайного вектора эхо-сигнала, отраженного от дождя сделанное в [1] не трудно видеть, что для того, чтобы оценка D _δ стала несмещенной, величину оценки m_j мы вынуждены формировать (копить) когерентно в каждом из квадратурных каналов по алгоритму (17). Вычисление оценки 15 _л в каждом из квадратурных каналов по выборочному алгоритму второго центрального момента все равно оставит ее смещенной, поскольку, при выполнении операции квантования, добавляется смещение этой оценки в виде второго слагаемого в выражении (15).

В когерентной измерительной системе (см. [17]) знак величины (амплитуды сигнала) xiT всегда определяется. Из [17] известно, что (18) это некогерентное накопление выборок (при возведении в квадрат теряется информация о знаке). Из [17] известно, что выигрыш сигнал/шум при некогерентном накоплении d _вых = о | _вых / о шш_вых ~ Nn . Выигрыш при когерентном накоплении d _{B ых} , = ( mi j )² О шв_вых ~ N . По этой причине для формирования оценки в соответствии с (17) объем выборки требуется меньший, чем при формировании оценки (18) при совпадающих дисперсиях оценок. Подставляя в (14) выражение для координаты (15) и учитывая то, что m j- = in j перепишем (14) в следующем виде:

ˆˆ

ˆ

P = DJ = Do

^{1   1   s} j

i

1,

_ˆ D nj

Л ² A ² v ( - 1 ) n

⁺ L TATexp ¹² ( n ) n = 1 ( n )

_2n °nn

I A2 J

^

Г2п - ^

cos —n m. + 2> K г

I A ')   i < j i¹^,

)

. (19)

Из [2, 3, 18] известно, что диапазон изменения d = о|вых jo^вых имеет место от значений о|, когда эхо от капель «спрятано» в шуме ош , до значений, когда о| может «занимать» весь ˆ динамический диапазон. Скорость сходимости оценки Pξi определяется величиной d. Здесь оценки Dˆξi требуют такие объемы выборок, чтобы оценка Kˆw , лежащая в пределах от 0,8312 до 0,9340 была сформирована с наперед заданной точностью. При этом формирование Kˆw не должно противоречить условию физической реализуемости измерения. Под реализуемостью следует понимать отсутствия изменений l (r0, Kw, R), Kw, R, M вызванных ветром. Тогда (19) это алгоритм адаптивного оценивания P мощности, отраженной от изотропной капельной струк-ξi туры (дождя), устраняющий также и влияние отражающей доминанты. По этой причине оценки

• σ ˆ и ε ˆ будут состоятельными и несмещенными.

Таким образом, видим, что если не отстроиться от сигнала отражающей доминаты, который

ˆˆ               ˆˆ при формировании оценки Dξ = Pξ накопится когерентно, то смещение оценок Dξ = Pξ может полностью исказить результаты радиофизических измерений и не позволить решить предпола-

Физика гаемые радиофизические и электрохимические задачи. Это произойдет по той причине, что m j ~ N, a D ~ VN , где N - объем выборки

^J              ^ J

• А, поскольку при формировании оценок берутся выборки нескольких импульсных объемов (на интервале времени определяющем физическую реализуемость системы), то несмотря на исчезающее малые значения второго слагаемого в формуле (15) , объем выборок столь велик, что сигнал отражающей доминанты в некоторых случаях сместит оценку D ^ˆ  до значений не позво-

• ξi

ляющих получить несмещенные оценки K_w , l ( r₀, K w , о ) , R и M и, соответственно оценки e: и σ ˆ станут не состоятельными.