Влияние вязкости растворителя на выход термализованных продуктов разделения зарядов из второго возбужденного состояния в производных цинк-порфиринов

Современная лазерная техника позволяет генерировать импульсы длительностью в несколько фемтосекунд в достаточно широком диапазоне частот, что позволяет исследовать динамику фотоиндуцированных превращений молекул в реальном времени. Недавно появились исследования переноса заряда с участием высших возбужденных электронных состояний (см.: [13–16; 19]). В этих экспериментах в качестве объектов исследования выступали производные цинк-порфиринов, что обусловлено двумя причинами: относительно большим временем жизни второго возбужденного состояния S ₂ (1–3 пс) и большим дипольным моментом перехода между состояниями S ₂ и S ₀ (основное состояние). Эти исследования показали возможность создания молекулярных переключателей [19], которые могут быть использованы в качестве элементов молекулярной электроники. Были синтезированы триады, включающие молекулу цинк-пор-фирина и два акцептора, ковалентно связанные с ним и находящиеся на противоположных сторонах порфиринового кольца. Параметры акцепторов удалось подобрать так, что первое возбужденное состояние S ₁ тушилось переносом электрона на один акцептор, а состояние S ₂ – на другой [19]. В такой системе можно управлять направлением переноса заряда, варьируя длину волны возбуждающего импульса и заселяя состояние S ₁, либо S ₂.

Целью данной работы является исследование влияния динамических свойств растворителя на кинетику разделения зарядов из второго возбужденного состояния и последующей рекомбинации в первое возбужденное и основное состояния производных цинк-порфиринов в рамках обобщенной стохастической модели и выявление растворителей, в которых разделение зарядов происходит с максимальной эффективностью.

• 1. Модель

Для описания сверхбыстрого разделения зарядов из второго возбужденного состояния и последующей рекомбинации зарядов в первое возбужденное и основное состояния используется минимальная модель, включающая четыре электронных состояния: основное состояние | S о ) , первое и второе синглетные возбужденные состояния, | S 1 ) , | S ₂ ) , соответственно, и состояние с разделенными зарядами, | CS ) (рис. 1). Эта модель, за исключением некоторых изменений, была ранее детально описана в работе [10]. Таким образом, мы только в общих чертах представим обозначения, используемые в дальнейшем.

Диабатические поверхности свободной энергии электронных состояний в терминах координат реакции Q_i ( i -я координата соответствует i -й моде среды) могут быть записаны как [5; 10]:

N

Q i ²

4 E ri

U_{S 2} = е i =1

• и% ) = е ( Q i - ² E ri ) + d g_c s + e n^

CS                                 CS          a a

4 E

• i=1             ria

N 2

U 1 m ) = У Q i - + ^A Gsvs 2 + У m„ ^a

S 1                           S 1 S 2

• i=1 4 Eria

N 2

• и ⁾ = у - Q i -+A G_{so я} + У l_ah^_a

S 0                      S 0 S 2

• i=1 4 Eria

где        W a ( a = 0, 1, 2,..., M) - частота a -й внутримолекулярной колебательной моды;

n _a , ^m _a , l _a ( ⁿ _a , ^m _a , l _a = 0, 1, 2,...) — квантовые числа a -й колебательной моды в состояниях | CS ) , | S 1 ) и | S 0 ) , соответственно;

A G CS - свободная энергия реакции разделения зарядов из второго возбужденного состояния;

D G _{S S} и D G _{S S} – разности свободных энергий между первым и вторым и между основным и вторым возбужденным состояниями, соответственно.

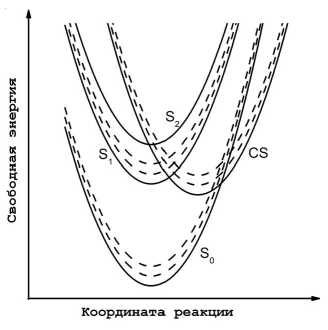
Рис. 1. Термы второго S ₂, первого S ₁ возбужденных и основного S ₀ электронных состояний и состояния с переносом заряда CS . Пунктиром изображены колебательные подуровни электронных состояний

Для описания временной эволюции системы применяется стохастический подход [3], обобщенный на случай многоуровневой системы [6; 20]. Этот подход применим для моделирования динамики разделения и последующей рекомбинации зарядов, когда вероятность горячего переноса электрона является значительной. Следует также отметить, что поскольку рекомбинация в S ₀ протекает на временах десятков пикосекунд, а время колебательной релаксации лежит в фемтосекундной области [12], то считаем, что переход CS ® S 0 протекает только из основного колебательного состояния CS . В рамках этого подхода временная эволюция системы описывается системой дифференциальных уравнений для функций распределения по координатам реакции [3; 20]:

¶rS2 ^                CS(

LS rS2 - е kn (rS2 - rCS )- kICrS2,

¶t

¶r C(nS)     ^      (n) CS             (n)             CR (n)      (m)                      (0)              1       (na' )             1

LCS rCS + kn (rS2 - rCS )- е  knm (rCS - rS1 )- dn0е  kl rCS + е   (na+1) rCS - е   (na) rCS ,

¶ t                                                _{m                                   l                a} t _{va                 a} t _va

ρS(m1 )     ^ (m)           CR     (m)       (n)                                   1 (m ')            1

— LS ps]    / , knm ( ps!   pcs ) + Omm*kiCps2 + / (m +1) ps 1    / , (ma) ps 1 ,

• ^d t                 m                                     a ^T v ^           a ^T v a

¶rS(l0) ^      (l)                   (0)                 1        (la')

LS rS0 + е kl rCS + е    (la+1)rS0 - е (la) rS0,

¶t                       l                 a t va                 a t va где rS2(Q,t) – функция распределения во втором возбужденном состоянии;

r_S ^{( m} ₁ ⁾ ( Q , t ) – на m -м подуровне первого возбужденного состояния;

r_S ^{( l} ₀ ⁾ ( Q , t ) – на l -м подуровне основного состояния;

ρ _C ^{( n} _S ⁾ ( Q , t ) – на n -м подуровне состояния с разделенными зарядами;

• m * – изоэнергетический с U_{S 2} подуровень первого возбужденного состояния;

• k_IC – скорость внутренней конверсии;

• Q – обозначает вектор с компонентами Q ₁, Q ₂, ..., Q_n ;

_L ˆ _СS и L ˆ _S – операторы Смолуховского, описывающие диффузию по термам U_CS и U_{S 2}, U_{S 1}, U_{S 0} соответственно:

N ж

ˆ =    1 1+ (Q - 2E ) ¶ + Q2 ¶,

LCS е                i rii i=1 t iзи               ¶Qi         ¶Qi чш

N

_L ˆ _S = е i =1

ж _t ¹ _{i з и}1+ Q i

¶₊ ¶ Q i

_¶ 2 ц ¶ Q i ² ч ш^,

Q_i ² = 2 E_rik_BT – дисперсия равновесного распределения по i -й координате; k_B – постоянная Больцмана, T – температура. Здесь предположено, что инерционная компонента релаксации среды может быть заменена дебаевской. Обоснование такой замены дано в работах [1; 2].

Зусмановские скорости переходов k_n^CS = k_n^CS ( Q ), k_nm^CR = k_nm^CR ( Q ) и k₁ = k₁ ( Q ) – между термами U „ и UC n ) , между U ⁽ nn ) и U ( ^m ) и между U £⁰J и U ( ' ) соответственно. В случае реакции

S 2       CS                cs        s ₁                    cs       s ₀

разделения зарядов и рекомбинации в основное состояние Зусмановские скорости определяются выражениями:

CS     2 pV n ² ж           ( n )ц      2      2

k n       h dU S 2 - U CS ш ^V n     V CS F n ,