Влияние влажности воздуха на взлетно-посадочные характеристики профиля крыла

Проблема воздействия неблагоприятных метеорологических условий на аэродинамику летателвного аппарата (ЛА) продолжает оставаться актуальной и в наше время [1]. Анализ аварий и авиакатастроф последних лет позволяет сформулировать перечень основных причин, приводящих к ним. По статистике доля влияния внешней среды (туман, ливень, резкое похолодание, высокая влажность воздуха, метель и др.) на эти происшествия доходит до 20%. Следует отметить, что более половины из них происходит на аэродромах, а треть — при взлете или посадке [2].

Понятно, что свойства среды, молекулярные и термодинамические, оказывают непосредственное влияние на обтекание ЛА. Известно, что влажность, влияние которой на плотность воздуха незначительно при низких температурах и достаточно велико при высоких температурах, приводит к уменьшению плотности влажного воздуха по сравнению с плотностью сухого воздуха [3,4].

(с) Врутяп М. А., Ие Хтуп, Павленко О. В., 2024

• (с) Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (национальный исследовательский университет)», 2024

2.    Параметрические исследования влияния влажности воздуха на максимальную подъемную силу профиля крыла 2.1.    Методика и условия расчета

Значения параметров атмосферы по высоте вычисляются по формулам для стандартной атмосферы [5] в предположении, что воздух является абсолютно сухим. В действительности же воздух всегда содержит некоторое количество паров воды, и его параметры отличаются от стандартных значений. Влажность воздуха необходимо учитывать при специальных баллистических расчетах, поскольку она влияет на плотность воздуха, скорость звука, скоростной напор и, в конечном счете, на величину аэродинамической силы, действующей на движущееся в воздухе тело [6].

Атмосферный воздух всегда является влажным, то есть представляет собой смесь сухого воздуха и водяного пара, и относится к типичным парогазовым смесям. При давлениях, близких к атмосферному, влажный воздух можно считать идеально-газовой смесью с той особенностью, что одна из компонент смеси (водяной пар) при определенных условиях может конденсироваться [7].

В настоящей работе приведены результаты численного исследования влияния влажности воздуха на аэродинамические характеристики профиля крыла во взлетной конфигурации в стандартной среде (воздухе) и в особых метеорологических условиях (тумане).

Для численного исследования взят профиль CLARC Y+ относительной толщины с = 12% при хорде b = 0.64 м и построена его взлетная конфигурация с отклоненным закрылком на угол ф_ак = 20° (рис. 1а, в) [8]. Закрыл ок имеет хорду, равную 1/3 хорды профиля крыла. Носовая часть профиля закрылка выполнена в виде дуги окружности, вписанной в верхнюю поверхность профиля. Ширина щели между основным профилем и закрылком равна 1.5 % хорды профиля (рис. 16).

а)

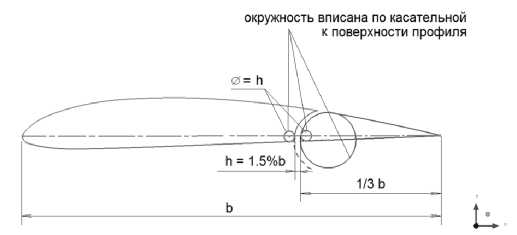
б)

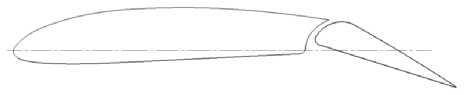
в)

Рис. 1. Профиль CLARC Y— с отклопеппым закрылком: а) исходный профиль, б) построение профиля с закрылком <5зак. = 0, в) взлетная конфигурация профиля, фак. = 20°

Расчеты выполнены в стационарной постановке по программе, основанной на решении осредненных по Рейнольдсу уравнений Навье - Стокса, на структурированной расчетной сетке, содержащей около 1 миллиона ячеек, из которых 150 расположены по хорде крыла (рис. 2). Для разрешения пограничного слоя была создана специальная сетка типа o-grid, построенная по нормали к поверхности и содержащая по высоте 20 ячеек. При моделировании области пограничного слоя высота первой ячейки, вблизи поверхности крыла, выбиралась такой, чтобы пограничный слой вместил достаточное количество ячеек для расчета пристеночной функции. Значение параметра у + в первом пристеночном узле было у+ С 0.365. В расчете использована Ce-realizable модель турбулентности [9] с учетом влияния градиента давления и улучшенным моделированием параметров турбулентности вблизи стенки. В пристеночной области использовалась однопараметрическая модель турбулентности, адаптированная к течениям в пограничном слое [10].

Рис. 2. Расчетная сетка вблизи профиля

Для расчета стационарного обтекания профиля с закрылком потоком влажного воздуха использовалась упрощенная модель среды «Mixture» [И]- в этой модели используется уравнение неразрывности V(pmVm) = 0, г де Vm = (^^=1 akPkVk ) /pm средняя массо-En                                             „ k=i akPk — плотность смеси, п — количество компонентов смеси; в рассматриваемом случае п = 2.

Уравнение импульсов для данной модели среды получено путем суммирования соответствующих уравнений для каждой компоненты:

^{V (}Pm V m V т) = -^VР + ^V [^m^(VVm + ^V V m)]

-∇

( n

E k=1

^ak ^pk V dr,k V dr,k

)’

где p_m = k=ka_k^akpk — вязкость смеси, a V d_r,k = V k - V _m ~ относительная скорость компонентов смеси.

Уравнение энергии для данной модели смеси газов имеет следующий вид:

n

V £ (akVk(PkEk + р)) = V(keff VT), k=i где keff — коэффициент эффективной теплопроводности, keff = kL1=kak(kk + kt)', kk — коэффициент молекулярной теплопроводности к-й компоненты смеси; kt — коэффициент турбулентной теплопроводности, определяемый в соответствии с используемой моделью турбулентности; Ek = hk — р/pk + V^/2 — для сжимаемой компоненты, е Е= = hk — для несжимаемой компоненты, где hk — энтальпия к-й компоненты смеси [11].

Величина плотности воздуха зависит от его температуры и влажности. Обычно стандартной величиной считается значение 1.225 кг/м3, которое соответствует плотности сухого воздуха при 15° С на уровне моря. Наличие водяных паров приводит к уменьшению плотности воздуха, что объясняется низкой молярной массой воды (18 г/моль) по сравнению с молярной массой сухого воздуха (29 г/моль).

Расчеты проведены в сухом и во влажном воздухе, который представляет собой смесь сухого воздуха с водяным паром. Согласно закону Дальтона давление смеси газов, занимающих определенный объем, равно сумме парциальных давлений всех ее компонентов. Влажный воздух можно рассматривать как смесь идеальных газов, в каждом из которых комбинация плотностей позволяет получить требуемое значение плотности смеси [12]. Данный подход используется в работе для моделирования тумана, в котором относительная влажность воздуха обычно весьма высока. Условия проведения параметрических расчетов в среде, состоящей из воздуха и водяного пара в различных их пропорциях, даны в табл. 1.

Таблица!

Условия проведения расчетов

Процент объема пара в воздухе р (%)	Плотность смеси p (кг/м3)	Динамическая вязкость смеси р • 105 (Па-с)	Число Рейнольдса Re-10—6
0	1.2250	1.79	3.46
8	1.1713	1.75	3.42
16	1.1177	1.72	3.33
25	1.0573	1.68	3.23

Из табл. 1 видно, что при увеличении объемного содержания пара уменвшается плот-ноств воздушной смеси, ее вязкоств, а также число Рейнолвдса смеси Re = pVb/p.

Численное исследование проведено для разрезного профиля с хордой b = 0.64 м, на угле атаки a = 12° при скорости набегающего потока V = 80 м/с, атмосферном давлении р = 101 325 Па, температуре окружающей средв! t = 15 °C, как в сухом, так и во влажном воздухе с размером частичек пара 10 мкм.

2.2.    Результаты расчета

Для различных пропорций воздуха и водяного пара с помощвю численного моделирования найден максимальный коэффициент подъемной силы с_у max профиля с закрылком и критический угол атаки а_кр.

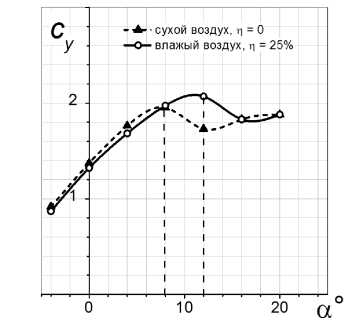
Рис. 3. Зависимости коэффициентов подъемной силы от угла атаки в сухом и влажном воздухе

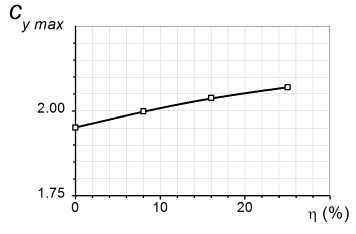
Рис. 4. Зависимости коэффициента максимальной подъемной силы профиля от процентного содержания пара в воздухе

Расчеты показали, что с увеличением влажности максимальная подъемная сила возрастает (рис. 3, 4). Соответственно увеличивается и критический угол атаки: при обтекании профиля крыла влажным воздухом при р = 25% значение а_кр. = 12°, а при сухом воздухе «кр. = 8° (рис. 5).

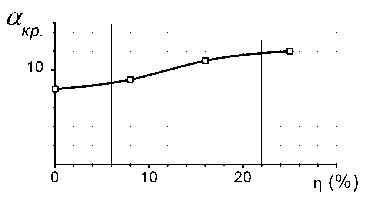
Рис. 5. Зависимость критического угла атаки от процентного содержания пара в воздухе

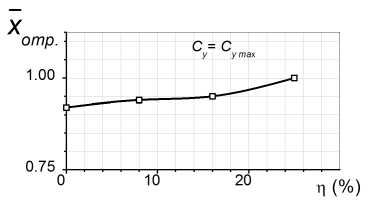
Рис. 6. Зависимость положения точки отрыва на закрылке от процентного содержания пара в воздухе

Увеличение с_у max и а_кр обусловлено тем, что с увеличением влажности воздуха положение точки отрыва пограничного слоя на закрылке смещается к его задней кромке. На рис. 6 показано относительное положение точки отрыва по хорде закрылка на режиме максимальной подъемной силы комбинации профиль + закрылок. Видно, что при ту = 25% отрыв на закрылке практически исчезает.

а)

б)

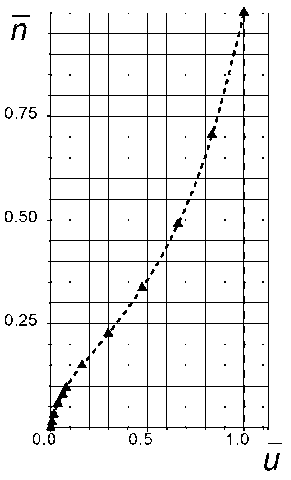
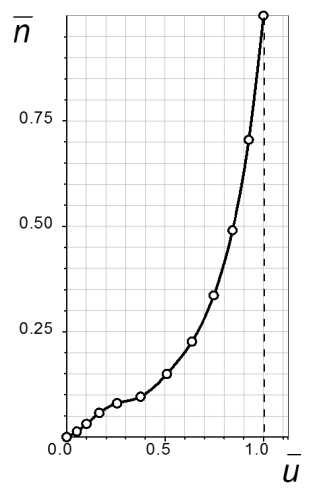
Рис. 7. Распределение скоростей в пограничном слое в точке на верхней поверхности закрылка х = 0.925;

а) - т = 0%; б) т = 25%

Профили скорости в пограничном слое на отклоненном закрылке при двух значениях концентрации водяного пара т = 0% нт/ = 25% приведены на рис. 7а, б. На этих рисунках значение скорости отнесено к скорости на внешней границе пограничного слоя, и = и/и_е, а расстояние по нормали к поверхности закрылка отнесено к толщине пограничного слоя, П = n/S.

Расчеты показывают, что в сухом воздухе точка отрыва расположена на расстоянии х = х/Ъ = 0.92 от носка закрылка. В этой точке зависимость й = й(п) при р = 0% имеет явно выраженный характер профиля скорости с нулевым трением, tw ~ (дй/дп^ ~ 0 (рис. 7а), в диапазоне 0.92 < х < 1 наблюдается возвратное течение, tw < 0. При увеличении влажности касательное напряжение tw на поверхности закрылка возрастает. При р = 25% точка отрыва смещается на заднюю кромку закрылка, а в точке X = 0.92 касательное напряжение становится положительным, tw > 0 (рис. 76).

3.    Заключение

Расчетные исследования по влиянию влажности воздуха на взлетно-посадочные характеристики профиля крыла с отклоненным вниз на 20° закрылком показали, что с увеличением влажности воздуха и соответствующим незначительным уменьшением числа Re наблюдается:

• —    увеличение коэффициента максимальной подъемной силы комбинации профиль + закрылок;

• —    увеличение критического угла атаки профиля;

— движение точки отрыва на закрылке к его задней кромке.

Вследствие того, что туманы располагаются около поверхности земли, то при взлете ЛА и его выходе из тумана при наборе высоты происходит смена влажного воздуха на более сухой. В работе установлено, что данное явление может представлять определенную опасность для ЛА, так как даже при небольшом уменьшении влажности воздуха максимальная подъемная сила может заметно уменьшиться. В проведенных расчетах получено, что при полете ЛА в сухом воздухе коэффициент максимальной подъемной силы уменьшается на 6%, а критический угол атаки - на 4° по сравнению с полетом во влажном воздухе с объемной концентрацией пара 25%.