Влияние внешнего электрического поля на зонную структуру графеновой наноленты

Носители заряда в графене описываются уравнением Дирака, а не привычным в твердотельной физике уравнением Шредингера, что обусловлено симметрией кристаллической решетки графена. Электронные подзоны, образованные симметричной и антисимметричной комбинацией волновых функций на разных подрешетках, пересекаются на краю зоны Бриллюэна, что приводит к конусообразному энергетическому спектру вблизи «дираковских» точек. Как следствие, квазичастицы в графене, подобно безмассовым релятивистским частицам, имеют линейный закон дисперсии E = й kv F , где роль скорости света играет скорость Ферми v_F « с /300 [4].

При положительных энергиях (выше дираковской точки) токонесущие состояния подобны электронам и заряжены отрицательно. При отрицательных энергиях, если валентная зона не целиком заполнена, квазичастицы ведут себя как положительно заряженные частицы (дырки) и могут рассматриваться как твердотельный аналог позитронов. Электроны и дырки в графене оказываются взаимосвязанными, проявляя свойства зарядово-сопряженной симметрии. Это обусловлено симметрией его кристаллической решетки и тем, что квазичастицы в графене описываются двухкомпонентной волновой функцией. Двухкомпонентное описание аналогично описанию в квантовой электродинамике (КЭД), использующему спинорные волновые функции, но «спин»-индекс в случае графена обусловлен принадлежностью разным подрешеткам, а не «реальному» спину обычных электронов, и поэтому именуется псевдоспином о.

Конический вид закона дисперсии в графене является результатом пересечения подзон, обусловленного разными подрешетками. В результате, электроны с энергией Е , движущиеся в положительном направлении, принадлежат той же ветви спектра, что и дырки с энергией – Е , движущиеся в противоположном направлении. Это означает, что электроны и дырки, находящиеся на одной и той же ветви спектра, имеют одинаковый псевдоспин о, который параллелен квазиимпульсу для электронов и антипараллелен для дырок. Это позволяет ввести понятие киральности [5], которая является проекцией псевдоспина на направление движения и имеет положительный знак для электронов и отрицательный для дырок.

Зонная структура графена была исследована и наиболее прямым способом – с помощью фотоэмиссионной спектроскопии с угловым разрешением, позволяющей установить рас- пределение электронов в импульсно-энергетическом пространстве [6]. Такое исследование показало, что хотя дисперсия вблизи дираковских точек и является приблизительно линейной, но она может искажаться вследствии различных взаимодействий. При сильном допировании графена вследствии электрон-электронного, электрон-фононного и электрон-плазмон-ного взаимодействий в дисперсионной зависимости при энергиях порядка 1 эВ появляются изломы [7; 8].

1.    Зонная структура бислоя графена

Одноатомной толщины графитовый лист с гексагональной структурой, называемый графеном, – пример двумерной системы с трансляционной симметрией. Он характеризуется двумя элементарными векторами трансляций С 1 и С 2 длиной с = V3 а 0 = 2,46 А , где а 0 = 1,42 А - длина связи между соседними атомами углерода (см. рис. 1).

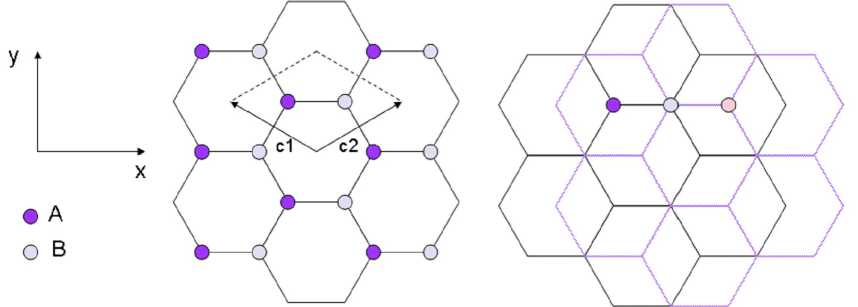
б

Рис. 1. Фрагмент слоя графена в плоскости ХУ

При рассмотрении двухслойного графена выбирается геометрическое расположение слоев, соответствующее АВАВ упаковке (графит Бернала).

Как и в однопериодической системе, оператор Гамильтона графена инвариантен относительно трансляций, поэтому его волновая функция должна удовлетворять теореме Блоха [2].

Для расчета зонной структуры бислоя графена предварительно вычислим значения интеграла перекрывания для волновых функций 2 p_z -орбиталей [3].

Расчет интеграла перекрывания проводился численно методом трапеций с точностью ~0,1 %. Значения резонансных интегралов определяются путем нормировки на величину резонансного интеграла электронного перехода между соседними атомами одного слоя (р 1 = 1,4 эВ) [2]. Результаты расчетов представлены в таблице 1.

Таблица 1

Значение величины интеграла перекрывания и резонансного интеграла в зависимости от смещения вдоль слоя

Δ y	0	а 0 /2	3 а 0 /2	а 0
S ab	3.55*10-5	2.41*10-5	1.14*10-5	7.94*10-6
β, эВ	2,49*10-3	1,69*10-3	7,98*10-4	5,56*10-4

Рассчитать волновые функции сложных систем невозможно, поэтому воспользуемся методом МО ЛКАО, то есть волновую функцию записывают в виде детерминанта, построенного из одноэлектронных волновых функций. В кристаллах с трансляционной симметрией волновые функции, зависящие только от координат электрона, называют блоховскими.

Для исследуемой системы базисные блоховские функции имеют следующий вид:

• ^У A ⁽ r ) = 17 T ^exP ^{{ i ( k1} 1 cl + kl 2 ^c 2 )} Pa ( r ^- l 1 c l ^{- 1} 2 ^c 2 )

L l 1 , l 2

• ^У B ⁽ r ^{) =} 17 T exP^ ¹ 1 c l + M 2 c 2 ^)} Pb ⁽ r ^- l c l ^- l 2 C 2 )

L l 1 , l 2

У_с ( r ) = —^= ^ exp {'( k/c + k1₁c₁ )} p_c ( r - d_x - 1c - l₂c ₂)

C             _{L l 1 , l 2}               1 1       2 2 C          1     1 1     2 2

• У d ( r ) =     T exp i U / i c + kl 2 c ₂ ^)} Pd ⁽ r - d ₂ - 1 1 c - 1 2 c 2)

L l 1 , l 2

где pA, pB, pC, pD – волновые функции атомных орбиталей; l1, l2 – целые числа; c1, c2 – векторы трансляций основной решетки; d1, d2 – смещения соседних атомов одного слоя графена относительно другого. В таком базисе, используя приближение ближайших соседей, определим секулярное урав нение четвертого порядка для законов дисперсии п-электронов:

det

а - E (У A H У в ) (У aH У с ) (У aH y d) (У b|H У A) а - E (V b|H У с) (у B H У d) (У CHУA) УС_СНУв) а - E УС_СН У _о) ( VdH У a) ^Н У в') (У d|H У с) а - E

= 0

Положение уровня Ферми совпадает с энергией p -орбитали а в свободном атоме углерода. Недиагональные матричные элементы записываются в приближении ближайших соседей:

(У A H |У _в ) = e _l ( l + e - kc + e ic )

(У A Н I V C ) = P 3 ( l + e - ikc + e i' )

(У A H |y _D ) = P ₃ ( e" ^c + e ² + e ik ⁽ c ² - ^{c )})

(У _в Н У A ) = e _l ( l + e ikc + e - k ^{—— 2} )

(Ув Н У с) = в 2

(У _в Н УУ = P ₃ (l + e   + e i⁴ )

(У _с Н У A ) = P ₃ ( l + e^ + e - kc ² )

(У с Н |У в ) = в 2

(У _с Н I y _D ) = Д ( l + e - ikc + e i '^{— 2} )

(У _d\H У a = e ₃ ( e i ^kc + e ~ ikc ² + e ~ ik ⁽ c ² - ^{C l )})

(У _DH У _B ) = в ₃ (1 + e⁸ ^ ' + e "ik - 2 )

(У _DH У C ) = в ₁ ( 1 + e ikc + e ~ ik )

где д = 1,4 эВ; в ₂ = 2,49 * 10 - 3 эВ; в ₃ = 5,56 * 10 ^{- 4} эВ - резонансные интегралы.

Подставив матричные элементы в секулярное уравнение, получим дисперсионное уравнение для бислоя графена:

а - E

det

1 —^

1 + e ikc

1 + e ik ⁵'

в ₃ ( e ik' + e - ikc 2

, - ikc-, + e c

+ e - ikc^

+ _e - ^{ik ( c} 2 c l )

в ₁ ( 1 + e- kc l + e^fc^ а - E

) в ₃ ( 1 + ek^ e - ^kc 2

)   в ₃ ( 1 + e - ikc + e^{,k —} 2

β 2

а - E

)   в ₁ (1 + e ik^ e - ikc

)   в ₃ ( e - ikc + e ikc + e k ⁽ c ² - ^{c —} )

n 11 . -i'kc i . ikc-> в з ( 1 + e ¹ + e ² в ₁ ( 1 + e - ikc¹ + e^{& —}

) а - E

= 0 .

Сдвигая энергию на уровень Ферми (а = 0), получаем уравнение четвертого порядка относительно собственного значения Е :

< /—*—* X    / —* —♦ X         / —* —♦

6cos l k-^{c l} - ^c 2- 1 cos f k— ¹ + - ² 1+ 2cos ² 1 kc¹- - ^ci

- 1 + 12cos 2 1 kc i^ c ² 1 + 8cos 3 1 kc l - c¹ 1 cosy c^c -11 + P^¹ + P 3⁴ ^ - 2 Д²Д 3² ^ ² + p ^ p^ -

^-^P\ ^P 2 ^P 3 ^{+ P} 2 ^P 3³ ) f ^6cO^ kc^^c² ^ cos f ^{kc L}2 ^{c i} ]^{+ 2C0S}f ^k—L₂C²

- 1 + 12cos 2 1 k c^{1 +c 2}

I 2

+

о _з li^— c i - c ₂ 1 _f ^— c + c ₂ 11 _А + 8cos3 l k ——² I coS k ——² 1 1 = 0

V 2 J V 2 JJ где

( —* —* \         / —* —* \                    / —* —*

5 = 1 + 4cos | k c —— I cos l k c ^{1 +} c ² I + 4cos ² 1 k c ^{1 +} c¹

I 2 J I 2 J I 2

Полученное уравнение описывает электронные переходы в бислое графена. Из уравнения видно, что переходы вдоль слоев и между ними взаимосвязаны. Учет электронных переходов между слоями приводит к расщеплению энергетических уровней по сравнению с зонной структурой монослоя графена. Это расщепление незначительно и его величина порядка резонансных интегралов p2, p3. Зонная структура бислоя графена показана на рисунке 2.

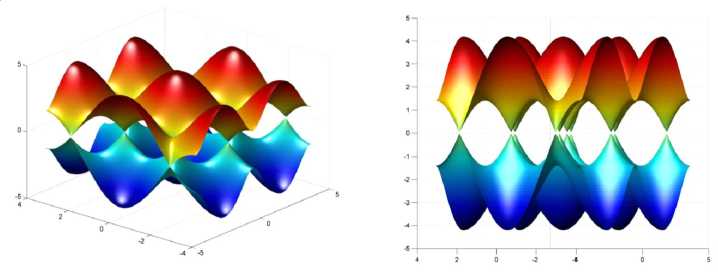
аб

Рис. 2. Зонная структура двойного графенового слоя:

а – по вертикальной оси отложена энергия, по горизонтальным – проекции волнового вектора kx,ky ; б – ось абсцисс – ky , ось ординат – энергия

2.    Влияние внешнего электрического поля на зонную структуру графеновой наноленты

Будем рассматривать ленты конечной ширины. В связи с этим на проекцию волнового вектора накладываются граничные условия. В итоге для лент zig-zag-типа проекция волнового вектора на ось Х принимает дискретный набор значений:

2 n   <  k <  2 n

a o ( 3 N - 1 )" x " 3 a T,

2πn kx = a0 (3N -1), где n =1 ^(N - 1), а для лент arm-chair-типа, соответственно:

2 п < k <  2 п

3a0N    y3

2πn ky = TSaON, где n = где N определяет ширину графеновой наноленты. Для расчетов использовались значения N = 5, 10, 15 гексагонов.

Рассмотрим постоянное тангенциальное электрическое поле, направленное поперек ленты. Гамильтониан системы электронов, в этом случае, в присутствии внешнего электрического поля, 1 dA- записанного в калибровке Кулона E =— —, в общем виде записывается:

H = £ ^e s p - - e ^{A (} t ) ] a + s a ps , ps V c )

где a ps , a_ps - операторы рождения, уничтожения электронов с квазиимпульсом (p , s ), A ( t ) = cEt -вектор-потенциал электрического поля, который имеет одну компоненту и направлен поперек графеновых нанолент; е s - закон дисперсии электронов [1].

Используя приближение времени релаксации ( т - 10 ^{- 13} с), поправка к импульсу преобразуется к виду eE τ , следовательно, учет внешнего электрического поля производится с помощью поправки к проекции волнового вектора на ось Х :

k

x

^ k x

eE τ

р -----. й

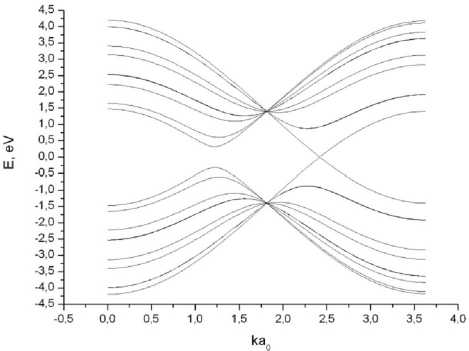
Влияние тангенциального поля на зонную структуру однослойной углеродной наноленты zigzag-типа показано на рисунке 3.

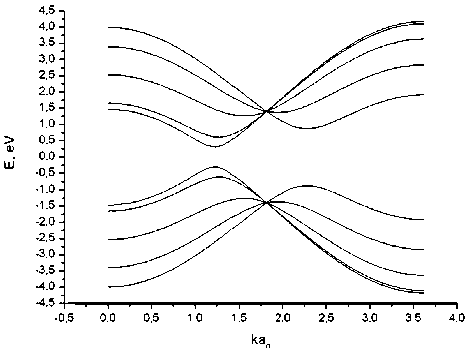
а

б

в

Рис. 3. Дисперсионные кривые графеновой наноленты шириной N = 5 гексагонов с учетом тангенциальной компоненты внешнего электрического поля:

а - Е _т = 0 В/мкм; б - Е _т = 13,8 В/мкм; в - Е _т = 41,4 В/мкм

С увеличением тангенциального электрического поля происходит изменение квазиимпульса электронов, что приводит к смещению разрешенных значений волнового вектора в зоне Бриллюэна и их периодическому прохождению через дираковские точки. В результате, это отражается на ширине запрещенной зоны, которая варьируется полем от 0 до 1 эВ.

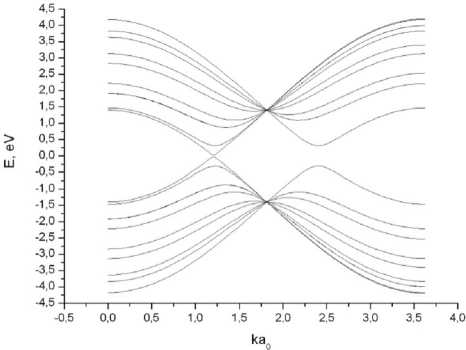
В случае двухслойной графеновой наноленты зонная структура с учетом внешнего тангенциального поля показана на рисунке 4.

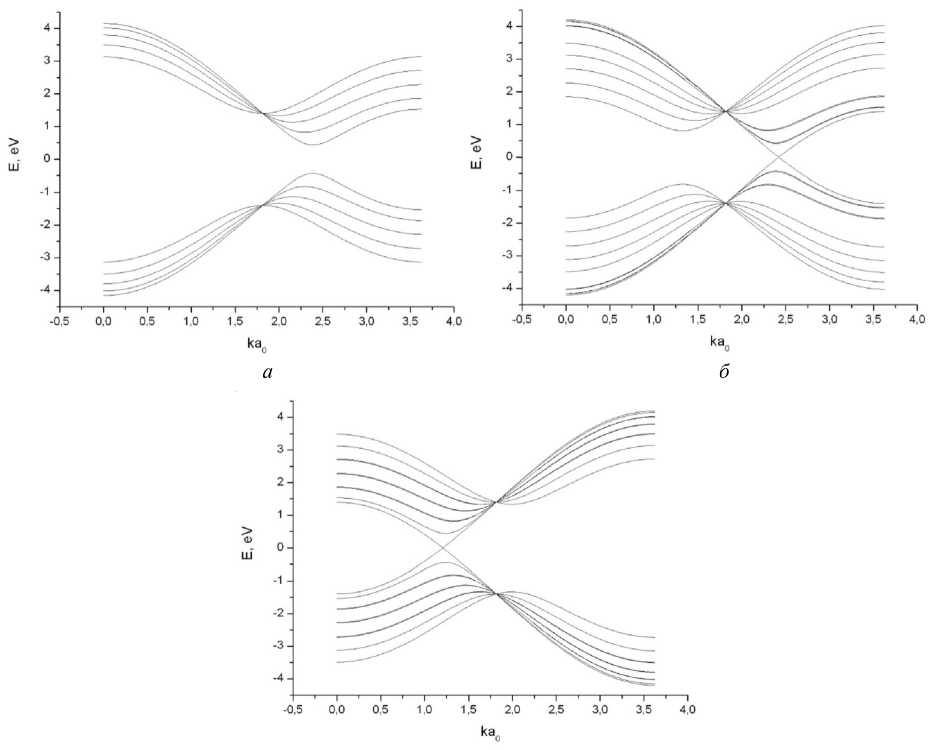
в

Рис. 4. Дисперсионные кривые двухслойной графеновой наноленты шириной N = 5 гексагонов с учетом тангенциальной компоненты внешнего электрического поля:

а - E _т = 0 В/мкм; б - E _т = 29,2 В/мкм; в - E _т = 87,4 В/мкм

Заключение

Приложение внешнего электрического поля в тангенциальном направлении по отношению к наноленте приводит к смещению разрешенных значений волнового вектора в зоне Бриллюэна. В результате уровни энергии периодически проходят через дираковские точки. Таким образом, происходит варьирование ширины запрещенной зоны в пределах от 0 до 1 эВ. Такое поведение должно существенно отражаться на проводящих свойствах объекта. В итоге мы получаем материал с переменными свойствами, управляемыми внешним электрическим полем.

Изменяя ширину лент, можно регулировать амплитуду и период изменения ширины запрещенной зоны.

В случае двухслойных нанолент также наблюдается дополнительное расщепление дисперсионных кривых за счет внешнего поля.