Влияние внешнего воздействия на развитие возмущений в орегонаторе с диффузией

С середины 60-х годов XX века и по настоящее время большое значение придается управлению режимом колебаний в химически реагирующих системах с помощью внешнего воздействия на исследуемую систему [1]. В работе исследуется облучение раствора (реакция Белоусова– Жаботинского) ультрафиолетовым излучением. С помощью УФ-излучения можно деформировать области существования колебаний и получать колебательные режимы при тех условиях, где их нет в отсутствие облучения. В экспериментах [1] были получены сложные режимы колебаний, которые наблюдаются в очень узких интервалах изменения параметров, и получить их с помощью подбора реагентов не удается. Также примеры теоретического и экспериментального изучения внешнего воздействия можно найти на биохимические, биологические процессы, описываемые уравнениями «реакция–диффузия» [2]. К числу актуальных проблем в биологии отно- сится динамика распространения числа пораженных клеток в живом организме, в том числе мутированных клеток при лейкемии, цитокининов при атеросклерозе [3, 4]. Ультрафиолетовое излучение – результат остановки клеточного цикла [5].

В данной работе представлены результаты математического моделирования в орегонаторе с учетом диффузии компонентов при внешнем воздействии. Показана возможность получения новых стационарных состояний, колебательного режима для автокаталитической реакции с диффузией. К математическим моделям химически-реагирующих систем как математически подобным обращаются в своей работе биологи, экологи.

Математическая модель орегонатора с учетом диффузии компонентов [6] и внешнего воздействия (параметр P ) имеет вид:

--= k AY - kXY + k^BX - 2 k₄X ² + D_x —-, dr 1        ²        3         4 X d 2

— = - kAY - k,XY + fk.Z + D_v —_T + P , d t     ^{1        2        5}       Y df

= k3BX - k5Z + Dz dZ, dt 3      5     Z df где X - концентрация бромистой кислоты HBrO2, Y - концентрация бромида Br , Z - концентрации церия IV, DX, DY, DZ – коэффициенты диффузии компонентов, f – стехиометрический коэффициент.

Стационарные состояния системы. Однородное стационарное состояние системы (1) определяется выражениями:

k 1 AY 0 - k ₂ X 0 Y 0 + k ₃ BX 0 - 2 k ₄ X 02 = 0, - k 1 AY₀ - k ₂ X 0 Y ₀ + fk ₅ Z 0 + P = 0, k 3 BX 0 - k ₅ Z 0 = 0,   (2)

где X 0 , Y 0 , Z 0 – концентрации компонентов, k 1 , k 2 , k 3 , k 4 , k 5 – константы скорости реакции.

Для входных параметров [7]: A = B = 6∙10–2, k1 = 8∙109, k2 = 2∙109, k3 = 2,1, k4 = 4∙107, k5 = 10–4 проведены вычислительные эксперименты по стационарному состоянию системы для различных значений стехиометрического коэффициента (табл. 1). Численное решение системы (2) проведено с использованием пакета Matlab как для случая отсутствия внешнего воздействия на систему, так и при внешнем воздействии.

Получены следующие результаты:

• 1.    Найденные стационарные решения являются положительными, что соответствует физическому смыслу автоколебательной химической реакции, которую описывает система (1).

• 2.    С ростом величины стехиометрического коэффициента увеличиваются значения величин X 0 , Y 0 , Z 0 .

• 3.    Внешнее воздействие при одних и тех же входных параметрах системы изменяет стационарное состояние (табл. 2).

Таблица 1

Стационарные решения системы в отсутствии внешнего воздействия

f	X 0 , 10–8	Y 0 , 10–17	Z 0 , 10–15
0,15	0,1811	0,0071	0,2282
0,25	0,1969	0,0129	0,2481
0,35	0,2126	0,0195	0,2679
0,45	0,2284	0,0270	0,2878
0,55	0,2441	0,0352	0,3076
0,65	0,2599	0,0443	0,3274
0,75	0,2756	0,0543	0,3473
0,85	0,2914	0,0650	0,3671
0,95	0,3071	0,0766	0,3870
1,05	0,3229	0,0890	0,4068
1,15	0,3386	0,1022	0,4267
1,25	0,3544	0,1163	0,4465
1,35	0,3701	0,1312	0,4664

Таблица 2

Стационарные решения системы при внешнем воздействии P = 0,8

f	X 0 , 10–4	Y 0 , 10–8	Z 0 , 10–10
0,15	0,99959264	0,16659767	0,12594867
0,25	0,99959343	0,16659793	0,12594877
0,35	0,99959421	0,16659819	0,12594887
0,45	0,99959500	0,16659845	0,12594897
0,55	0,99959579	0,16659872	0,12594906
0,65	0,99959657	0,16659898	0,12594916
0,75	0,99959736	0,16659924	0,12594926
0,80	0,99959775	0,16659937	0,12594931
0,85	0,99959815	0,16659950	0,12594936
0,95	0,99959893	0,16659977	0,12594946
1,05	0,99959972	0,16660003	0,12594956
1,15	0,99960051	0,16660029	0,12594966
1,25	0,99960129	0,16660055	0,12594976
1,35	0,99960208	0,16660081	0,12594986

Из приведенных данных табл. 2 видно, что при величине внешнего параметра, равного Р = 0,8, отмечается практически одно значение стационарного состояния для всего диапазона стехиометрического коэффициента. Величина внешнего параметра P = 0,8 зафиксирована в экспериментах Жаботинского [1] и является практически предельным значением, при котором возможны результаты, имеющие физический смысл. Для значений внешнего параметра P <  0,8 такого результата не наблюдается, стационарные решения для различных f положительны и различны.

Колебательный режим. Для вышеприведенных в табл. 1 и 2 стационарных состояний, значений стехиометрического коэффициента из диапазона 0,15 ≤ f ≤ 1,35 численно исследована методом Рунге–Кутта система обыкновенных дифференциальных уравнений (1) без учета диффузии компонентов.

Физика

Получены следующие результаты:

• 1.    В орегонаторе при отсутствии внешнего воздействия ( P = 0) устанавливается колебательный режим (рис. 1). Из экспериментальных данных [1, 9, 10] известно, что форма колебаний определяется в основном начальными концентрациями компонентов. Система выходит на колебательный режим через некоторый промежуток времени после смешения реагентов.

• 2.    С увеличением значения стехиометрического коэффициента время выхода на колебательный режим уменьшается.

• 3.    Также время выхода на колебательный режим сокращается (рис. 2) в результате внешнего воздействия на систему.

• 4.    При увеличении значения параметра Р , что в натурных экспериментах соответствует увеличению интенсивности облучения исходного состояния системы, отмечается уменьшение ам-

  плитуды колебаний, а также изменение периода колебаний.

  

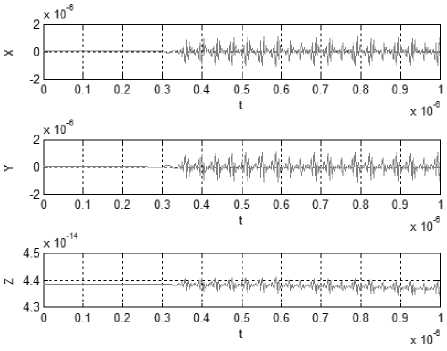
  Рис. 1. Изменение концентраций компонентов при f = 1,2, P = 0

  
  
  

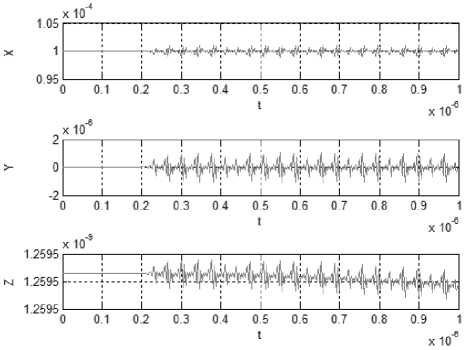
  Рис. 2. Изменение концентраций компонентов при f = 1,2, P = 0,8

  
  

Влияние диффузии компонентов. В физико-химических, биохимических, биологических системах, где химические реакции сочетаются с диффузией компонентов, диффузия может играть и дестабилизирующую роль [8]. Так называемая диффузионная неустойчивость приводит к возникновению в исследуемых системах устойчивых пространственных структур. Стационарные структуры возникают в работающих реакторах и наблюдались в экспериментах при исследовании реакции Белоусова–Жаботинского. Первые экспериментальные режимы были получены в конце 60-х и начале 70-х годов 20 века как российскими учеными Жаботинским А.М., Заикиным

А.Н., Вавилиным В.А. [9, 10] так и иностранными учеными Busse H.G. Kaufman M. [12], Beck M.T., Varadi Z.B. [13].

[11], Herschkowitz-

Для изучения нелинейного развития возмущений в орегонаторе, полагая X = X о + x , Y = Y + y , Z = Z о + z осуществим переход от системы (1) к системе в возмущениях x , y , z :

LU = N ,

где

U=I x I' L=

к z 7

(-дт

^^^^^^^s

Dx ~,

X d^

^{- b} 2

^- c l

к

^^^^^^^s

a ₁

- a - 2

к

д п д2

"т--Dy —5— b дт Yд^2   1

b ₃

, N =

д дт

^^^^^^^e

D

d 2

*7

Z д £ ²

^^^^^^^e

c 2

a 3 xy + a 4 x b4 xy

0 к

.

Исследуя устойчивость стационарного состояния (2) по отношению к возмущениям x (^, t ) = exp (k^ - tot), получим дисперсионное уравнение

ai + ia - k 2 DX        a 2              0 b 2        bi + ia - k 2 DY        b3 ci              0        c 2 + ia - k 2 DZ = 0 или соответственно a3 - ipia3 + p2a- ip3 = 0,                                   (4)

где to = to r + i a i , to r - частота возмущений, a t - скорость роста возмущений.

Коэффициенты дисперсионного уравнения (4) имеют вид:

pi = al + bi + c 2 - K2( DX + DY + DZ ) , p2 =(ai + bi - K2(DX + DY))(c2 - K2DZ ) + (ai - k2DX )(bi - K2DY )- a2b2 , p з =( ai - K dx )( bi - K Dy )( C 2 - K dz ) + a 2 b ci - a 2 b2( C 2 - K dz ), ai = -k2Y + k3B - 4k4Xо, a2 = ki A - k2Xо, a3 = -k2, a4 = -2k4, bi = - ki A - k 2 X0, b2 = - k2 Y0, b3 = fk5, b4 = - k 2, ci = k3 B, c 2 = - k5, где K – волновое число.

Решение уравнения (4) проведено с использованием пакета Matlab. Вычислительный эксперимент по расчету частоты, скорости роста возмущений осуществлен для коэффициентов диффузии D X = 0,008, D Y = 0,016, D Z = 0,00001.

Получены следующие результаты:

• 1.    Для диапазона стехиометрического коэффициента 0,15 ≤ f ≤ 1,35 представленная модель орегонатора с учетом диффузии компонентов неустойчива, скорость роста возмущений ω i > 0 (табл. 3).

• 2.    Необходимо выделить два неустойчивых режима:

• 1)    смена устойчивости ω i > 0, ω r = 0;

• 2)    колебательная неустойчивость ω_i > 0, ω_r > 0.

• 3.    Для различных значений волнового числа получаются различные колебательные режимы. Кривые скорости роста возмущений для режима смены устойчивости показаны на рис. 3.

• 4.    Стехиометрический коэффициент является бифуркационным параметром системы, при изменении которого в орегонаторе меняется тип неустойчивости. С увеличением стехиометрического коэффициента возрастает скорость роста возмущений в системе, она становится более неустойчивой (рис. 3).

Таблица 3

Значения частоты и скорости роста возмущений для f = 0,55

K	ω r , 10–8	ω i
1	–0,0056	0,2910
3	0	0,3594
5	0,0777	0,4962
7	0	0,7015
9	0,0444	0,9752
11	0,0888	1,3173
13	–0,0888	1,7278
15	–0,3553	2,2068
17	–0,3997	2,7542
19	–0,0444	3,3700

Физика

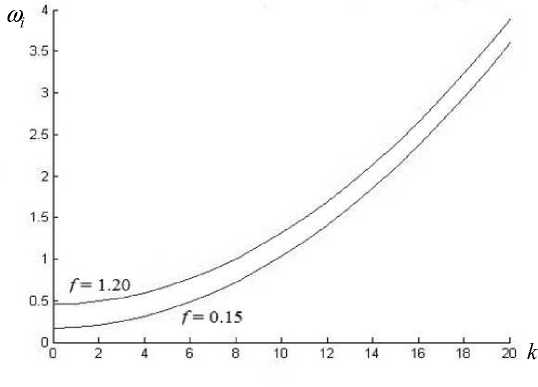
Рис. 3. Зависимость скорости роста возмущений от волнового числа для различных значений f

Заключение. Показано изменение стационарного состояния и режима колебаний автокаталитической системы (орегонатора) при внешнем воздействии. Установлен диапазон значений стехиометрического коэффициента, при котором система с диффузионным типом связи неустойчива. Время выхода на колебательный режим сокращается с увеличением стехиометрического параметра.