Влияние вращательных вибраций на течения и тепломассообмен при выращивании кристаллов германия вертикальным методом Бриджмена

Одним из наиболее распространенных методов выращивания полупроводниковых кристаллов является вертикальный метод Бриджмена. Конвективные движения, возникающие в расплаве, могут приводить к неоднородному распределению примеси в выращиваемом кристалле [1]. Поэтому весьма актуальным является поиск способов управления конвективными движениями и поведением границы раздела расплав/кристалл в процессе затвердевания. В качестве одного из таких способов предложено вибрационное воздействие. В работе [2] исследовано влияние высокочастотных вибраций на морфологическую устойчивость бесконечного плоского фронта кристаллизации, движущегося с постоянной скоростью. Выяснено, что, в отличие от случая поверхности раздела несмешивающихся жидкостей, высокочастотные нормальные вибрации оказывают дестабилизирующее действие, а касательные вибрации играют стабилизирующую роль. На основании этих результатов было сделано предположение о том, что вращательные вибрации вокруг оси ампулы могут привести к стабилизации морфологической неустойчивости фронта при направленной

кристаллизации бинарных сплавов. Численное исследование течений и тепло массообмена при направленной кристаллизации модельных прозрачных бинарных систем с низкой температурой кристаллизации в присутствии вращательных вибраций высокой частоты и малой амплитуды, проведенное в [3], показало, что такие вибрации генерируют течение, локализованное вблизи фронта кристаллизации, причем направление течения противоположно гравитационно-конвективному течению; взаимодействие вибрационного и гравитационно-конвективного течений приводит к оттеснению гравитационно-конвективного вихря от фронта кристаллизации. Численное исследование влияния вращательных вибраций на морфологическую устойчивость фронта при направленной кристаллизации модельных систем проведено в [4]. Расчеты показали, что вращательные вибрации действительно повышают порог морфологической неустойчивости. В настоящей работе представлены результаты численного исследования влияния вращательных вибраций на конвективные течения и сегрегацию примеси при кристаллизации вертикальным методом Бриджмена реальных бинарных сплавов с высокой температурой плавления.

Во многих работах исследование течений и тепломассообмена в процессах кристаллизации проводится с использованием методов конечных разностей или конечных элементов. Однако, применение этих методов к исследованию тепло- и массопереноса при кристаллизации бинарных сплавов может приводить к физически некорректным результатам из-за невыполнения условия сохранения массы. Эта проблема не возникает при применении метода конечных объемов (МКО) (см. работу [5], в которой проведено сопоставление метода конечных элементов и МКО при решении задач направленной кристаллизации бинарных сплавов).

Модель и численное решение

Конфигурация метода направленной кристаллизации схематически изображена на рисунке 1. Нагрев с помощью печи моделировался путем задания внешней эффективной температуры Т_в ( z, t ) , профиль которой принимался линейным Т в ( z . t ) = T + ( Т - Т )( z - Z p )/ L .

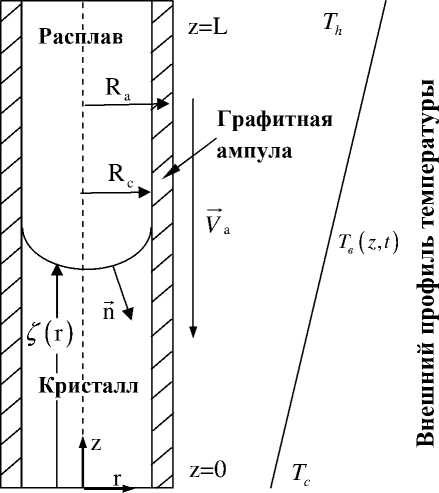
Рис.1 . Геометрия задачи

Расплав рассматривался как несжимаемая ньютоновская жидкость. Применялось приближение Буссинеска. Использовался квазистатический подход, при котором скорость движения фронта кристаллизации V_a считается равной скорости вытягивания ампулы из печи. Распределение концентрации в начальный момент времени C ₀ полагалось однородным. Задача решалась в осесимметричной постановке, что позволяло ввести функцию тока ψ и завихренность течения ω :

1 ∂ ψ u =-       ,

ρ _lr ∂ z

1 ∂ψ     ∂u ∂v v=        , ω=   -   ,

ρl r ∂r       ∂z ∂r где u — радиальная, а v — вертикальная компоненты скорости. Определяющие уравнения в терминах функции тока и завихренности имеют следующий вид:

д ( to ду д r V r д z

∂

+

∂ z

-

-

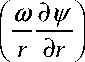
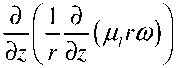
f о д T  _o д C I

+ ^p i g I ^в т    - ^вс~=Г I = 0,

V    д r       д r )

∂ ∂ z

I - 7 1

V P i r ^д Z )

∂ +

f 1 ду I

^{д r} V P i r ^{д r} )

+ω=

0,

∂

∂ r

∂ ∂ z

= 0,

д ( д _{( x} д ( д C I д ( д C )

— ( ruC ) + — ( Tv^C )^- — I ^rDi — I ^- — I ^rD i I = 0. д r д z д z V д z ) д r V д r )

Здесь µ _l — динамическая вязкость расплава, ρ _i — плотность, C_pi — удельная теплоемкость теплопроводных фаз i (символом i обозначены величины, соответствующие: l — расплаву; s — кристаллу; a — ампуле), g — гравитационное ускорение, β _T и β _C — коэффициенты температурной и концентрационной зависимости плотности соответственно и D_i — коэффициент диффузии в i -той фазе.

На всех твердых границах, включая границу раздела фаз, ставились условия прилипания, на оси ампулы — условия симметрии

I - У I ;

V P i r ^{д r} )

11 - т I ^д z V P i r ^д z )

r = ^R c : У = ¹ P s ^V a ^Rc \     ^to =-l" ^f    ^ ^ ;

2                    д r V P l r д r )

\ T ^{1        2} д I 1 ду )

z = ^Z ( r ) , L : У = -P s ^V a r , ^to = — ;

2                 д z V P l r д z )

r = 0: ψ= 0, ω= 0.

Для температуры на внешней стенке ампулы задавался линейный закон теплоотдачи. На границе раздела расплав — кристалл z =ζ(r) считалось выполненным условие баланса энергии, температура полагалась равной равновесной температуре ликвидуса в соответствии с диаграммой фазового состояния T = Tm0 + mC , где m — наклон линии ликвидуса.

Влияние высокочастотных вращательных вибраций ампулы вокруг ее оси с угловой амплитудой α и частотой ω учитывалось с помощью эффективного граничного условия для касательных компонент скорости на твердых границах, полученного в [3] и имеющего вид:

α ² ω r u =        sin ϕ ,

τ ₄

где r — двумерный радиус-вектор точки на твердой границе; ϕ — угол между касательной к фронту и осью вращения; p _v = α ² ω — параметр, характеризующий интенсивность вибраций.

Для концентрации примеси на фронте кристаллизации ставилось условие баланса вещества:

Dn ∇ C - (1 - k ) ρ ^s CV_ane = 0,                                             (6)

ρl где k — коэффициент сегрегации.

На границе раздела расплав — ампула считалось выполненным условие отсутствия потока вещества:

• r = R c : ^{∂ C} = 0 .                                                                        (7)

∂ n

На верхней границе расплава для концентрации ставилось граничное условие, обеспечивающее вместе с условием (6) сохранение примеси:

• - Dn ∇ C - ρ ^s ( C ₀ - C ) V_a = 0.                                                 (8)

ρ _l

Здесь C ₀ — средняя концентрация примеси в кристалле вблизи фронта кристаллизации.

Метод решения

Для перехода от физической области с искривленным фронтом кристаллизации к вычислительной прямоугольной области уравнения и граничные условия записывались в обобщенных криволинейных координатах [5]. В дивергентной форме универсальной для всех неизвестных величин уравнения имели вид:

d (

( a ^^W d n l ^ф d^ J a ; (

-

+

d ( b

d; ( J t g-

∂ ( c φ ) ∂ η

11 +

( b

d ( W) d aφ   +

\^г д п л 1 dn ( J t

∂

т I g 22

-

^d( с ф ) ' g ¹² d ^

∂ ( c φ ) ∂ξ

-

^d( с ф )' ^g 12 ^ T J

и+ Jd = 0,

где φ — искомая функция; a , b , c — коэффициенты соответствующих уравнений; g ₁₁, g ₁₂, g ₂₂, J — коэффициенты перехода к криволинейным координатам:

f dr, т + f dz; > 2

V ^dn J v ^dn J

^g 22

f a r 2 + f a z > 2

V a # J I a# J

∂r ∂r   ∂z ∂z      ∂r ∂z   ∂r ∂z g =      +      , J=      -

¹² ∂ η ∂ ξ ∂ η ∂ ξ ^,    ∂ η ∂ ξ ∂ ξ ∂ η

.

Коэффициенты преобразования координат выбирались таким образом, чтобы обеспечить сгущение сетки вблизи фронта кристаллизации и границ расплава с ампулой. Параметры сгущения указаны в таблице 1. Преобразование координат аналогично [5].

Для построения дискретного аналога рассматриваемой задачи применялся метод конечных объемов. Расчетная область разбивалась на ячейки дискретизации, при этом получалась сетка размерностью n × m , где n — число узлов по горизонтали, m — по вертикали. Вокруг каждого узла сетки строился конечный объем из отдельных частей ячеек дискретизации, примыкающих к соответствующим узлам. Линейный индекс ячейки дискретизации получался по формуле k = i + ( j - 1) n , где i = 1, ... , n — нумерация горизонтальных узлов, а j = 1, ... , m — вертикальных.

Рассматривалась ячейка дискретизации, состоящая из четвертинок конечных объемов Ω _k , Ω _{k + 1}, Ω _{k + n} , Ω _{k + n + 1} , построенных вокруг узлов сетки k , k + 1, k + n , k + n + 1 (Рис. 2). Границы между конечными объемами обозначались символом Γ и определялись индексами соответствующих соседних конечных объемов.

Интегрирование уравнения (9) по всем конечным объемам согласно теореме Остроградского – Гаусса дало систему уравнений следующего вида:

j f ^{а ф} ^У# - I ^{f а ф} ^ 1 d n ⁺ J"

Г k # ^V

d# J

Г k n V

дП J

Г k # V

b

—A

J

∂ ( c φ ) g 22 _∂ η

-

д ( с ф )' g ¹²   d #

>

J

⁺ I ^b ^ । g 11 “ ( c ^ ) ^- g 12 “ ( c ^ ) I ^{П +} I ( ^Jd ) ^d ^ ^k = ^0, Г n V J I ^d # ^d n J     П_k

где k — номер узла сетки расчетной области

Следующий шаг в построении дискретного аналога рассматриваемой краевой задачи состоял в аппроксимации входящих в интегральные соотношения (10) значений искомой функции φ и ее производных по соответствующим координатам.

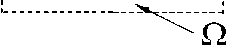
Рис.2 . Ячейка дискретизации, состоящая из четвертинок конечных объемов

При использовании технологии поузловой сборки конечно-объемной системы алгебраических уравнений [5] для замены интегробалансного соотношения (10) его дискретным аналогом было необходимо определить, какие из частей границы Г _к конечного объема Q _к лежат внутри расчетной области, а какие являются частями внешних границ. Кроме того, конечные объемы для граничных узлов могли состоять из различного числа четвертинок ячеек дискретизации, а сами четвертинки могли быть по-разному расположены по отношению друг к другу (например, две четвертинки ячеек дискретизации лежат внизу и одна четвертинка в углу). Трудоемкость получения полного дискретного аналога системы интегральных уравнений (10) повышалась как из-за сложностей программирования, так и по суммарным вычислительным затратам на обработку одного узла сетки. В настоящей работе для построения дискретного аналога интегробалансных соотношений (10) использовался другой подход, основанный на поэлементной сборке конечнообъемной системы алгебраических уравнений (см., например, [6, 7]).

Рассматривалась ячейка дискретизации с узлами k , к + 1, k + n , k + n + 1. Получаемые от нее вклады в интегробалансное соотношение для конечного объема Q _к равнялись:

J Vd n + J Hd n + J ( Jd ) d Q _k ,

^Г к , к + 1               ^Г к , к + n               ^Q к

А дУ Ь

V — аф--1— д^  J

g ₂₂

д( сф)      д( сф)

П g ¹² д^

Аду b

H = - a o   + — ^ g 11

дп J

д ( сф)      д ( сф)

--g 12    ---- д^ дп

Вклад для объема Q _{к + 1} составлял:

- J Vd n + J Hd n + J ( Jd ) d Q _{к + 1}-

^Г к , к + 1               ^Г к + 1, к + n + 1                ^Q к + 1

Вклады для объемов Q и Q     записывались аналогично.

к + n        к + n + 1

ЛГ    а ду , b [     ^д( ^{с ф} )      ^д( ^{с ф} )

Аппроксимация        интеграла    аф —^!— + ^ g 22-- g ₁₂----- f

Гк к+1    д^ J I дп д- рассматриваемой ячейки дискретизации имела вид:

для

( ^ф к ^{+ ф} к + 1 ) ( ^ак ( У к + n У ) ^{+ а}к + 1⁽ У к + n + 1 ^У к + 1 ) ^{+ а}к + n ( У к + n ^- У к ^{) +} а к + n + 1 ( У к + n + 1 ^- У к + 1 ) ) ₊ 24

+

bk g22k к Зк

+ ^Ьк + 1

^Jk + 1

^g 22 к + 1

+

^Ьк + n

^Jk + n

g 22 к + n

+

ь ик+n+1

^Jk + n + 1

^g 22 к + n + 1

^{( с}к + 1 ^ф к + 1

Скфк )

h n

( b b , b              b ,          ^

Y g 12 к +      g 12 к + 1 + T+ n g 12 к + n +        g 12 к + n + 1

к ^ к J к + 1 ^ к + n ^ к + n + 1 7

( ^ск + n ^ф k + n ^{- с}к ^ф к ) ₊ ( ^ск + n + 1 ^ф к + n + 1 ^{- с}к + 1 ^ф к + 1 )

h§                  h^          h^

После прохода по всем ячейкам дискретизации получалась система линейных алгебраических уравнений (СЛАУ), аппроксимирующая систему интегральных уравнений задачи без учета граничных условий. Матрица при векторе неизвестных собиралась из коэффициентов при соответствующих компонентах вектора неизвестных, входящих в аппроксимируемый интеграл; она имела девятидиагональную структуру. Для завершения формирования СЛАУ сначала выполнялся проход по всем внешним границам расчетной области, на которых заданы граничные условия для потоков наблюдаемых функций. Затем учитывались граничные условия с заданными значениями функции на границе. Для этого граничное значение функции заносилось в соответствующее место вектора свободных членов, а в соответствующей строке матрицы неизвестных недиагональные элементы приравнивались нулю, а диагональные — единице.

Для решения СЛАУ использовался метод GMRES с предобуславливателем ILU [8] из пакета SPARSKIT [9]. Число узлов вычислительной сетки выбиралось на основании анализа результатов тестовых расчетов, из требований точности вычислений и оптимизации затрат машинного времени. В основных расчетах использовалась сетка размерностью 61×21 (в кристалле), 61×121 (в расплаве), 10×141 (в материале ампулы). Расчеты проводились для бинарной системы GeGa. Физические и геометрические параметры приведены в таблице.

Численные результаты

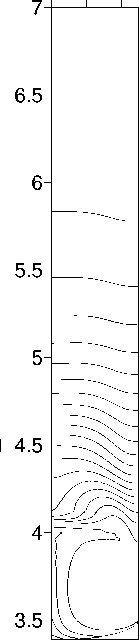
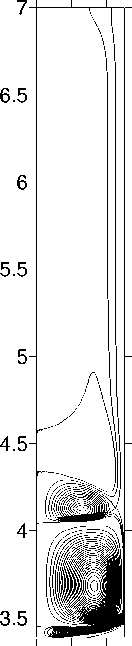
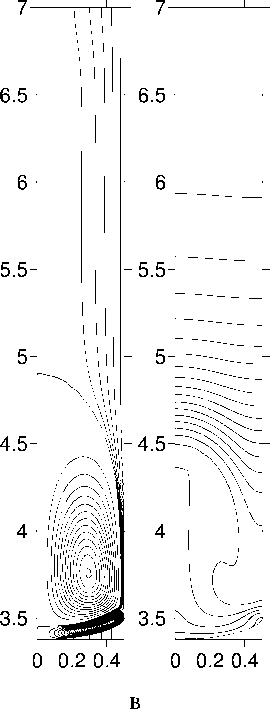
Результаты численных расчетов приведены на рисунках 3–6. На рисунках 3 и 5 показаны изолинии функции тока и концентрации примеси в расплаве при скорости движения нагревателя V a = - 0.0004 см / с в отсутствие вибраций и при наличии вибраций различной интенсивности. Минимальные и максимальные значения полей функции тока и концентрации на рисунках приведены без указания единиц измерения, поскольку они одинаковы на протяжении всей статьи: единицы измерения функции тока — кг / с , концентрация измеряется в весовых процентах — вес%. Поля функции тока, представлены в системе отсчета, связанной с ампулой. Для получения более полного представления о картине течения изолинии функции тока, соответствующие отрицательным и положительным значениям у , изображены через разные интервалы.

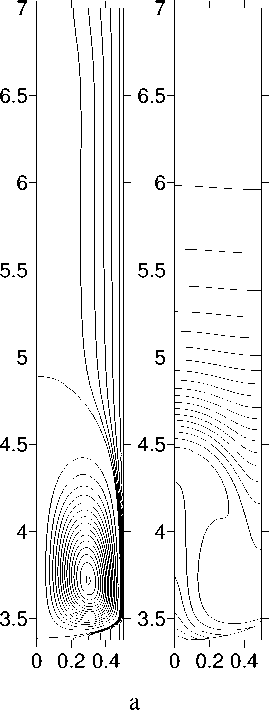
Рисунок 3 соответствует кристаллизации в земных условиях: Ra T = 2.489 х 10⁸. Положительные линии тока представлены на этом рисунке через 0.002 кг / с , отрицательные — через 0.0001 кг / с . Из рисунка видно, что в отсутствие вибраций в расплаве вблизи границы раздела жидкой и твердой фаз возникает гравитационноконвективный вихрь (Рис. 3, а). Направление циркуляции в вихре таково, что вблизи фронта кристаллизации расплав движется от стенки ампулы к оси симметрии (положительные значения функции тока). Это приводит к значительной неоднородности распределения примеси на фронте: примесь скапливается вблизи оси ампулы.

Вращательные вибрации индуцируют течение, направленное противоположно гравитационному. Как видно из сопоставления фрагментов 3, а и 3, б, вибрации умеренной интенсивности оказывают слабое влияние на течение и распределение примеси при Ra T = 2.489 х 10⁸. Эффект вибраций становится заметным лишь при достаточно больших значениях вибрационного параметра p _v . При увеличении p _v до 4.9 х 10 ^{- 1} с ^{- 1} интенсивность вибрационного течения достигает интенсивности гравитационно-конвективного течения и вибрационный вихрь оттесняет гравитационный от фронта кристаллизации (Рис.3, в).

Таблица. Физические свойства и входные параметры системы GaGe

Плотность твердой фазы, ρs	5.5 г/см3
Плотность жидкой фазы, ρl	5.5 г/см3
Температура плавления чистого германия, T m0	937.4°C
Скрытая теплота плавления, АН	460 Дж/г
Коэффициент теплопроводности расплава, κl	0.17 Вт/(см°C)
Коэффициент теплопроводности твердой фазы κs	0.39 Вт/(см°C)
Удельная теплоемкость твердой фазы, C ps	0.39 Дж/(г°C)
Удельная теплоемкость жидкой фазы, C pl	0.39 Дж/гК
Коэффициент теплового расширения расплава, βT	5.0 10-4°C-1
Коэффициент динамической вязкости, µl	0.00715 г/(см сек)
Наклон линии ликвидуса, m	0°C(вес% Ga)-1
Концентрационный коэффициент расширения расплава βC	0 (вес% Ga)-1
Коэффициент сегрегации, k	0.087
Коэффициент диффузии Ga в расплаве, D l	2.1 10-4 см2/сек
Ампула (Графит)
Плотность материала ампулы, ρa	1.8 г/см3
Коэффициент теплопроводности материала ампулы, κa	3.26 Вт/(см°C)
Удельная теплоемкость материала ампулы, C pa	1.814 Дж/(г°C)
Другие входные параметры
Коэффициент теплоотдачи, h	46.571 Вт/(см2°C)
Температура холодной зоны, T c	1112.4°C
Температура горячей зоны, T h	762.4.°C
Длина ампулы, L	7 см
Внутренний радиус ампулы, R c	0.5 см
Внешний радиус ампулы, R a	0.7 см
Параметры сгущения

Радиальная координата в расплаве и кристалле	6 = 3.0
Вертикальная координата в расплаве	6 m = 2.5
Вертикальная координата в кристалле	B = 1.3

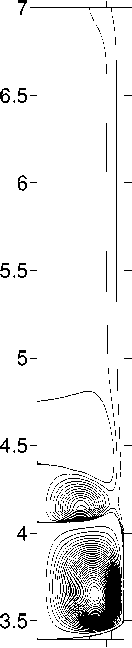
0 0.2 0.4

0 0.2 0

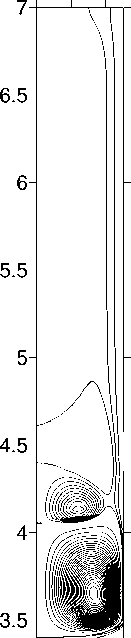
0 0.2 0.4

0 0.2 0.4

0 0.2 0.4

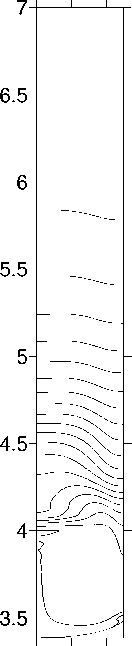
0 0.2 0.4

а

б

^ min =- 1.26 Х 10 " 3

^ max = 5.58 Х 10 " 2

C min = 1.052, C max = 13.03

^ mi, =" 1.07 Х 10 " ³

^ max = 5.56 Х 10 " ²

C min = 1.053, C max = 12.92

в

^ min =- 7.19 Х 10 ^{- 3}

^ max = 5.10 Х 10 " ²

C min = 1.053, C max = 11.37

Рис.3. Поля функции тока и концентрации для скорости движения ампулы V a = - 0.0004 см / с :

а — p v = 0 с ¹; б — p v = 0.049 с ¹; в — p v = 0.490 с ¹

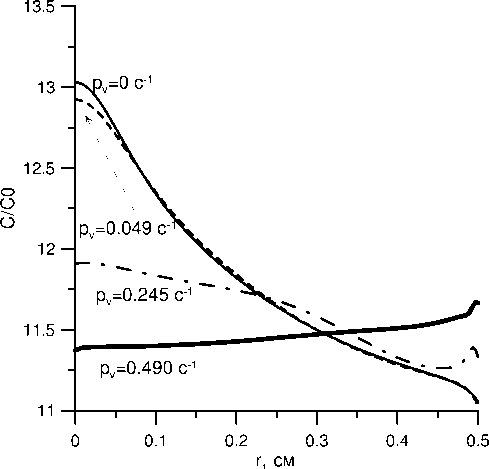
Рис.4. Распределение относительной концентрации вдоль фронта кристаллизации для Ra T = 2.49 Х 10⁸ и разных интенсивностей вибраций

^ min =- 2.75 Х 10 ^{- 4} , ^ .  = 7.55 X 10 ^{- 3}

C min = 1.070 , C max = 13.46

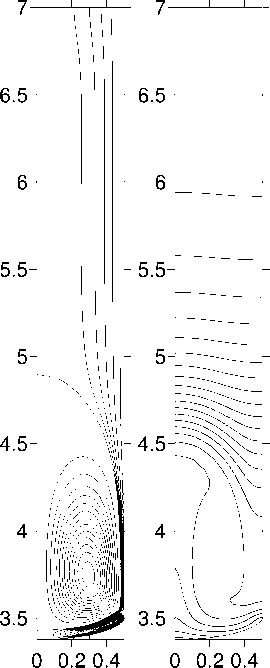
б

F min =- 1.07 X 10 ^{- 3} ^ max = 6.84 ХЮ- 3 C min = 1.064 , C max = 12.26

^ min =- 1.72 Х 10 ^{- 3}

^ max = 6.56 ХЮ- 3

C min = 1.063 , C max = 11.66

Рис.5. Поля функции тока и концентрации для скорости движения ампулы V a = - 0.0004 см / с : а — p v = 0 с ^{- 1}; б — p v = 0.049 с ^{- 1}; в — p v = 0.074 с ^{- 1}

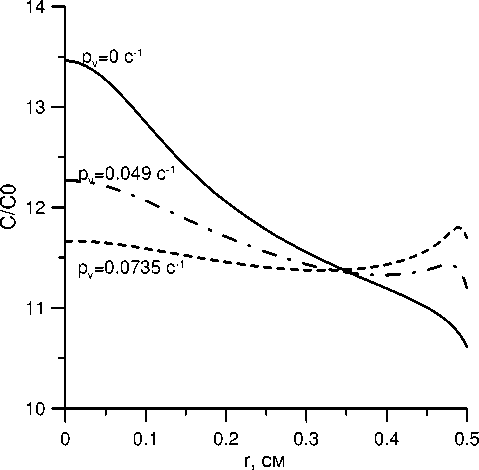
Влияние вращательных вибраций на радиальную сегрегацию примеси при кристаллизации в земных условиях иллюстрирует рисунок 4, на котором представлены распределения концентрации галлия на фронте кристаллизации в отсутствие и при наличии вибраций различной интенсивности ( p v = 0.049; 0.245; 0.49 с - 1 ). Как видно, с увеличением интенсивности вибраций распределение концентрации становится более однородным. При p v = 0.49 с - 1 концентрация галлия практически однородна вдоль фронта.

Заключение

Проведено численное моделирование течений и тепломассообмена при выращивании кристаллов вертикальным методом Бриджмена под действием высокочастотных вращательных вибраций. Для дискретизации уравнений и граничных условий применен метод конечных объемов. Расчеты, проведенные для бинарной системы GaGe, показали, что при кристаллизации в земных условиях существенного эффекта можно достичь лишь при вибрациях достаточно большой интенсивности: практически однородное распределение примеси на фронте кристаллизации получено в расчетах при a² to = 0.49 c ¹. В условиях пониженной гравитации распределение концентрации на фронте кристаллизации становится однородным уже при малых интенсивностях вибраций.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 05–01–90556) и Национального научного совета Тайваня (контракт RP05E40).