Влияние вращения на каскадные процессы в спиральной турбулентности

Среди факторов, способных влиять на классический (колмогоровский) сценарий поведения развитой турбулентности несжимаемой изотермической электрически не проводящей жидкости, особо выделяются два: общее вращение и спиральность. Вращение приводит к снижению скорости диссипации энергии, связанному с подавлением каскадного переноса энергии от больших масштабов к меньшим. Влияние силы Кориолиса распространяется только на большие масштабы, ограниченные волновым числом k _Q = ( s/Q 3 ) (здесь s — скорость диссипации энергии, Q — угловая скорость вращения системы) [1]. Для крупномасштабной части спектра ( k <  k _Q ) простые феноменологические рассуждения приводят к закону: E ( k ) к ( Qs ) ¹ / ² к - 2 [2]. Вывод этого закона основан на предположении, что спектральный поток должен быть пропорционален характерному для данного масштаба времени взаимодействия, которое равно времени оборота системы Q^{- 1} на больших масштабах и времени оборота вихря на малых масштабах ( k >  k _Q ), где устанавливается обычный колмогоровский спектр E ( k ) ^ с ^{2 3} k ^{- 5/1} . Закон « - 2 » нашел подтверждение в численных (например, [3]) и в экспериментальных [4] исследованиях.

Спиральность (точнее, плотность спиральности) определяется как интеграл от скалярного произведения скорости и завихренности H = (1/ V )J_K( v rot и ) dV и является интегралом движения в идеальной трехмерной гидродинамике несжимаемой жидкости. Спиральность может иметь любой знак, а в большинстве реальных потоков ее среднее значение просто равно нулю, что соответствует неспиральной, то есть колмогоровской турбулентности. Среди возможных сценариев влияния спиральности на турбулентность обсуждались самые различные, вплоть до появления обратного каскада энергии на фоне прямого каскада спиральности, но численные исследования спиральной (но однородной и изотропной) турбулентности показали, что спиральность переносится по спектру вместе с энергией, не меняя закона распределения спектральной плотности энергии [5, 6].

Можно отметить, что среди обсуждаемых механизмов генерации спиральной турбулентности важное место занимает сила Кориолиса, которая совместно с градиентом поля плотности (давления, интенсивности турбулентных пульсаций) может приводить к генерации спиральности. В этой связи возник интерес к изучению совместного влияния вращения и спиральности на статистические свойства развитой турбулентности. Моделирование свободного вырождения спиральной и неспиральной турбулентности при наложении общего вращения показало, что в отсутствие вращения спиральность не влияет ни на закон убывания общей энергии, ни на распределение энергии по спектру, а во вращающейся турбулентности

спиральность приводит к более крутому спектру энергии (« - 2,5 » вместо « - 2 ») и к заметному замедлению темпа вырождения [7]. Численное моделирование вынужденной спиральной турбулентности с вращением, выполненное в работе [8], подтвердило, что в присутствии вращения каскад спиральности существенно воздействует на динамику мелкомасштабной турбулентности, хотя численный эксперимент и не позволил воспроизвести развитый инерционный интервал.

В моделировании динамики действительно протяженных инерционных интервалов вне конкуренции остаются каскадные модели турбулентности. Каскадные модели — это системы обыкновенных дифференциальных уравнений гидродинамического типа, которые с помощью относительно небольшого числа переменных описывают процессы спектрального переноса в развитой турбулентности. Каскадные модели адекватно передают особенности нелинейного переноса в трехмерной и двумерной турбулентности, динамику пассивных примесей, температуры и магнитного поля в широком диапазоне определяющих параметров [9]. В то же время вопрос возможности применения каскадных моделей для изучения влияния вращения на динамику турбулентности остается открытым. Это связано с тем, что каскадная модель, оперирующая скалярными переменными, не позволяет выделить какое-либо направление, а информация о размерности пространства содержится только в представлении интегралов движения. Таким образом, учет влияния вращения на динамику турбулентного переноса осуществляется косвенно и сводится к принятию во внимание эффектов, обусловленных влиянием силы Кориолиса.

Попытки описать влияние вращения на спектральное распределение энергии в рамках популярной каскадной модели, известной под аббревиатурой GOY (Gledzer–Okhitany–Yamada), изложены в работах [10–13]. Однако особенности модели GOY, в силу специфики определения второго интеграла движения — спиральности, не позволяют корректно представить спектральное распределение и поток спиральности. Попытка одновременного рассмотрения влияния спиральности и вращения предпринята в работе [14], где предложено достаточно сложное обобщение модели для анизотропной турбулентности.

Цель данной работы состоит в развитии каскадных моделей изотропной, но спиральной турбулентности с учетом силы Кориолиса.

2.    Каскадная модель и сила Кориолиса

Изучение влияния вращения на механизмы переноса энергии и спиральности будем вести на основе каскадной модели спиральной турбулентности [6]:

U T n = ik n Y i [ U 2-1 + ( U n -1 ) 2 + в ( U n U n +i - U„*U : ₊ i ) - в ² ( U . U n +1 + U . U *+1 ) ] +

^[u .U + U * .U + ^(U* .U*-U .iH-Hl/²+(l/*

- Re ^{- 1} к ² U + F + F„ C , n n n ,

Y 2     n-1   n       n-1   n           n-l^ n       n-r^ nJ   M I    n+1    у   n+1 J  I где β — параметр, определяющий ширину интервала волновых чисел; γk —свободные параметры; Re — число Рейнольдса; Fn — внешняя сила, обеспечивающая приток энергии в систему; FnC — внешняя сила, о которой речь пойдет позже. Уравнения (1) записаны для каскадных переменных Un = an + i bn, каждая из которых является характеристикой пульсаций скорости в интервале волновых чисел kn < к < kn+1, где kn = вn. Символ «*» означает комплексное сопряжение. В расчетах использовались значения параметров Y1 = 1, Y2 = -в 5/2, предложенные в работе [15] исходя из оценок числа взаимодействующих вихрей различных размеров.

E = Z Un Г =Е( a.‘+ b2)    и nn

Уравнения (1) имеют два интеграла    движения:

H = - У k„^U *)² - U 21 = У k„a„b, n n     n       nnn

4 nn

соответствующие энергии и спиральности. Действие силы

Кориолиса описывает слагаемое F_c , для которого в данной работе использовалось две модели.

Первая модель имеет вид:

FnC = - '^ Un (t).

Такая сила действует независимо в каждом отдельном масштабе, вплоть до диссипативного, и формально осуществляет поворот фазы комплексной переменной Un на величину, пропорциональную скорости вращения Q . Формула (2) предложена в работе [10], авторами которой отмечено, что она позволяет учитывать особенности вырождения турбулентности во вращающейся жидкости, но при попытках рассмотрения стационарно возбуждаемой турбулентности приводит к высоко коррелированным состояниям, характеризуемым близостью к нулю суммы фаз комплексных переменных трех соседних ярусов. При этом процессы спектрального переноса оказываются блокированными. Чтобы избежать физически не обоснованного синхронного поворота фазы на разных масштабах, в [11] использовалась сила вида (2), в которой Q включала среднее значение и флуктуирующую добавку. В данной работе сила выражается, как в работе [16], где Q остается постоянной по модулю, но меняет знак по случайному закону через характерное время т = 1]Q.

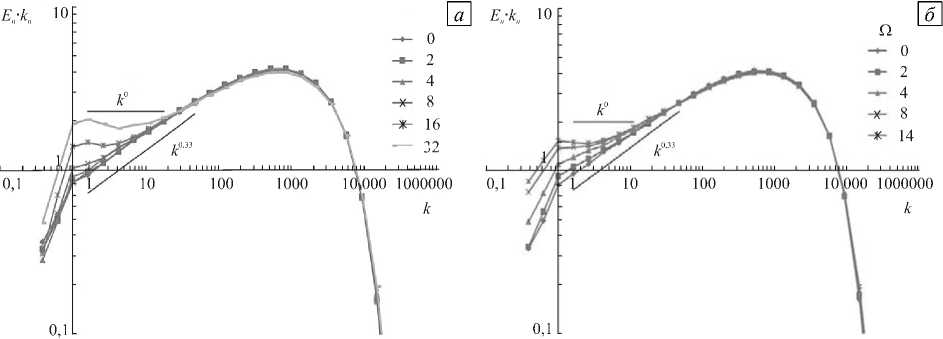
Результат численного интегрирования уравнений (1), включающих силу (2), для стационарно возбуждаемой турбулентности при числе Рейнольдса Re = 10 5 и различных значениях параметра Q приведен на рисунке 1, а . Представлены средние значения энергии, умноженные на волновое число, при этом закону « - 2» соответствует горизонтальная линия. Спектральные распределения энергии показывают, что увеличение Q вызывает накопление энергии в области больших масштабов. Спектр становится круче, и на больших масштабах в нем появляется участок, близкий к распределению E ( k ) ~ к - 2 , хотя настаивать на наличии участка с фиксированным степенным законом трудно. Диапазон масштабов l , до которого распространяется действие силы Кориолиса, соответствует при этом оценке l >  l Q = ( e/Q 3 ) 1/ ² [1].

Таким образом, сила в виде (2) описывает известное влияние вращения на каскадный перенос энергии по спектру, замедляя его на больших масштабах. Недостатком такой модели силы является то, что она влечет непосредственное изменение спиральности на каждом масштабе (что противоречит закону сохранения спиральности), хотя в среднем (по времени или по всему спектру) спиральность сохраняется, так как сила F_n^C произвольно меняет знак. Отметим, что в случае магнитогидродинамической турбулентности такая модель работает вполне удовлетворительно, так как сохранение спиральности не требуется [16].

Построить для силы модель, не вносящую в систему ни энергии, ни спиральности, можно только при согласованном воздействии на соседние ярусы. Вклад искомой силы, обозначим ее F_n^C , в изменения действительных и мнимых частей пары каскадных переменных U n и U n _{+ 1} запишем как a_n = Re ( F C ) = A n , a_{n + 1} = Re ( F C ) = B n _{+ 1}, b n = Im ( F C ) = C_n . Для определения величин A n , B n , C n , D_n , являющихся реальными и мнимыми частями искомого выражения силы, потребуем сохранения энергии в каждом ярусе

I по отдельности (anan + bnbn = 0 и a,

I

'n _{+ 1} a n _{+ 1} + b n _{+ 1} b n _{+ 1} = 0) и сохранения спиральности в паре ярусов

((anb3n + b„an) + в(an+1 bn+1 + bn+1a n+1) = 0 )■ Принимая одну из величин, например, An = 1, находим остальные три компоненты силы, действующей в двух соседних ярусах, для второй модели a (а2 - b(b2 - a2) (b .- a n n n                   C          n n      n + 1      n + 1

-■       :—■       = ; F , = ---,       :—,       = ■ 7 a n + ^b 2 7 a 2+1 + ^b 2+1            P 7 a n + ^b 2 7 a 2+1 ^{+ b} 2+1

Результаты численного интегрирования уравнений (1) с силой по модели (3) для числа Рейнольдса Re = 10⁵ и значений параметра Q = 0, 4, 8,12 и 14 приведены на рисунке 1, б . Сравнение рисунков 1, а и 1, б показывает, что обе силы качественно правильно отражают влияние вращения на спектральное распределение энергии турбулентных пульсаций: происходит накопление энергии на больших масштабах; колмогоровское распределение энергии нарушается; в области больших масштабов реализуется интервал,

— 32

Рис. 1. Компенсированные спектры энергии для различных значений параметра Q : сила Кориолиса имеет вид (2) - ( а ) и (3) - ( б )

в котором спектральное распределение энергии приближается к закону E ( k ) ~ к ². Однако спектральное распределение спиральности для силы, действующей в двух ярусах, значительно отличается от той картины, которая получается для силы, действующей в одном ярусе.

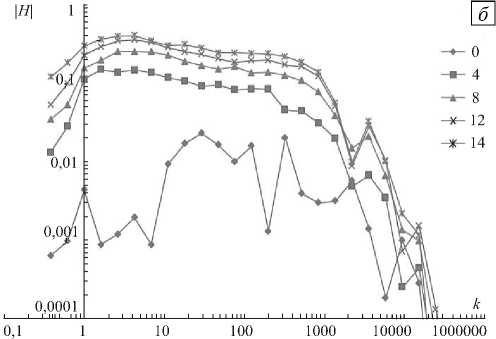
Рисунок 2 демонстрирует спектральные распределения средней спиральности для некоторых значений параметра Q , полученные при использовании моделей силы (2) и (3). Из рисунка 2, а видно, что при действии силы (2) распределение спиральности носит нерегулярный характер. Уровень спиральности остается низким по сравнению со значением полной энергии системы ( E ~ 1, а H ~ 10 ^{- 3}). При использовании силы (3) спектр спиральности, показанный на рисунке 2, б , становится более заполненным, причем в пределах инерционного интервала спиральность сохраняет знак. С увеличением параметра Q происходит рост полной спиральности системы, а спектральное распределение спиральности следует закону H ( к ) ~ к ~^и0. Таким образом, сила Кориолиса (3) вызывает рост полной спиральности в системе, причем сама сила не вносит в систему спиральность. Рост спиральности в системе вызван слабым потоком спиральности с малых масштабов.

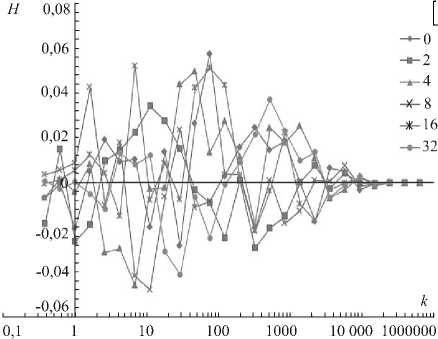
Рис. 2. Спектральное распределение спиральности при различных значениях параметра Q для моделей силы Кориолиса (2) – ( а ) и (3) – ( б )

Влияние спиральности на динамику каскадного процесса во вращающемся турбулентном потоке проще всего выявить при исследовании эволюции свободно вырождающейся турбулентности, поскольку в этом случае снимается вопрос о свойствах внешней силы, а уровень спиральности определяется только начальными условиями.

Эволюция свободно вырождающейся турбулентности исследована численно для четырех видов начальных условий:

E = 1, H = 0, Q = 0 — неспиральная турбулентность без вращении;

E = 1, H = 1, Q = 0 — спиральная турбулентность без вращения;

E = 1, H = 0, Q = 10 — неспиральная турбулентность с вращением;

E = 1, H = 1, Q = 10 — спиральная турбулентность с вращением.

В начальный момент времени спектральное распределение энергии отвечало колмогоровскому закону E ( к ) ~ к ^{- 5/3}, а общая безразмерная энергия системы равнялась единице (при этом Re = 10 5 ). Спиральность (в случаях спиральной турбулентности) также была единичной и распределялась по закону H ( к ) ~ к ^{- 5/3}, что соответствовало сценарию переноса спиральности как пассивной примеси, описанному в работах [6, 17].

Для каждого типа начальных условий было просчитано 20 реализаций с небольшим случайным шумом в начальных условиях. Графики скорости вырождения турбулентности для Re = 10 5 приведены на рисунке 3, а , где показаны зависимости общей энергии системы от времени для четырех обсуждаемых видов начальных условий. Каждая кривая получена путем осреднения по 20 реализациям. Можно видеть, что в отсутствие вращения спиральность практически не меняет характера вырождения турбулентности (см. кривые 1 и 2 ), что согласуется с результатами работ [6, 17].

Вращение значительно замедляет темп вырождения, что связано с блокировкой каскада и удержанием энергии на больших масштабах, где действие вязкой диссипации несущественно. В то же время при наличии вращения появляется различие в эволюции неспиральной и спиральной турбулентности. На ранних этапах вырождения (t -10 < 5, в момент времени 10 прекращается подкачка энергии) спиральная турбулентность с вращением теряет энергию так же быстро, как и турбулентность без вращения. Затем темп вырождения падает до уровня темпа вырождения неспиральной турбулентности, а на поздних стадиях эволюции энергии спиральной и неспиральной турбулентности становятся приблизительно одинаковыми.

Рисунок 3, б содержит результаты аналогичного численного эксперимента, но для существенно меньшего значения числа Рейнольдса: Re = 450, которое использовалось в вычислениях работы [7]. Существенное различие в скорости диссипации энергии между спиральным и неспиральным случаями при наличии вращения не наблюдается (кривые 3 и 4 ), что в некоторой степени не согласуется с результатами [7]. Однако при столь малых значениях числа Рейнольдса выраженный инерционный интервал отсутствует, энергонесущий и диссипативный масштабы близки и каскадные процессы играют менее заметную роль. При больших числах Рейнольдса зависимость от спиральности пропадает (Рис. 1, а , кривые 2 , 4 ), что подтверждает представления о спиральности в каскадных процессах как о пассивной примеси.

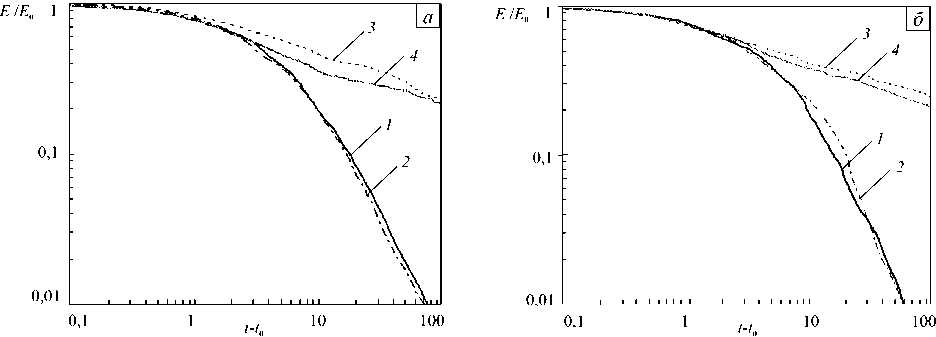
Рис. 3. Эволюция общей энергии системы при значении Re = 10 ⁵ ( а ) и Re = 450 ( б ) при свободном вырождении спиральной и неспиральной турбулентности в отсутствие и при наличии вращения, соответствующем начальным условиям: (4) 1 - кривая 1 ; (4) 2 - 2 ; (4) 3 - 3 ; (4) 4 – 4

3.    Заключение

C помощью каскадной модели спиральной турбулентности, включающей силу Кориолиса, численно исследованы каскадные процессы при больших числах Рейнольдса. Во-первых, показано, что вращение снижает интенсивность каскадного переноса энергии по спектру и приводит к накоплению энергии в крупномасштабной части спектра, что согласуется с результатами работ [2–4]. В то же время важно отметить, что наклон участка спектра энергии, в котором происходит накопление энергии, зависит от угловой скорости вращения Q и соответствует закону к ^{- 2} лишь в определенном диапазоне ее значений. С увеличением параметра Q спектральное распределение становится более крутым. Интервал масштабов, до которого распространяется влияние силы Кориолиса, определяется не только интенсивностью вращения Q , но и скоростью диссипации энергии е и соответствует теоретическим оценкам [2]. Во-вторых, подтверждено, что вырождение турбулентности замедляется в присутствии вращения, но при этом спиральность слабо влияет на скорость диссипации.

Формулировка выражения для силы Кориолиса в рамках каскадных моделей составляет самостоятельную проблему. Представляется, что стохастический характер силы и выполнение закона сохранения спиральности являются необходимыми условиями её успешного решения. Можно отметить, что предлагаемый в данной статье вариант рандомизации модели силы Кориолиса проще, чем в работе [11]. Что касается сохранения спиральности, то идеального решения нет. В случае силы (2) спиральность сохраняется лишь в среднем, а использование силы (3) приводит к дополнительному обмену между соседними ярусами. Спектральное распределение спиральности зависит от выбора модели силы Кориолиса.

По-видимому, точное решение проблемы может быть найдено в классе анизотропных каскадных моделей, попытки построения которых уже предпринимаются. Действительно, вращение является причиной возникновения анизотропии, и трудно ожидать, что все связанные с ней эффекты могут быть учтены в рамках каскадных моделей изотропной турбулентности. Другой подход может состоять в использовании каскадных моделей, способных воспроизводить геострофический баланс сил. В работах [10, 18] показано, что в главном порядке разложения по числам Экмана сила Кориолиса компенсируется градиентом давления. Тем не менее, полученные результаты кажутся вполне удовлетворительными, и предлагаемая формулировка силы Кориолиса может успешно применяться для построения комбинированных моделей генерации крупномасштабных полей [19]. Основной механизм генерации за счет турбулентности основан, как правило, на действии альфа-эффекта, который в свою очередь возникает в спиральной турбулентности.

Работа выполнена при финансовой поддержке РФФИ и администрации Пермского края (проекты № 11-01-96000-р_Урал_а и № 11-01-96031-а). Также Р.А. Степанов выражает свою признательность за финансовую поддержку Совету по грантам Президента РФ (грант МД-4471.2011.1).