Влияние временной структуры портфеля на показатели минимального объема экономического капитала коммерческих банков и вероятности дефолта заемщиков
Автор: Помазанов Михаил вячеславовиЧ., Глушкова Александра александровнА.
Рубрика: Экономическая теория и мировая экономика
Статья в выпуске: 1 т.7, 2013 года.
Бесплатный доступ
Статья посвящена проблемам определения адекватной величины экономического капитала, необходимого для создания резервов в банковском секторе. Рассмотрены основные модели (Васичека) и подходы, которые легли в основу предложенной в Базеле 2 формулы штрафа на капитал за превышение портфельных сроков до погашения одногодичного временного горизонта. В статье авторы критически рассмотрели проблему недооценки кредитного риска для заемщиков с высокими рейтингами.
Минимальный уровень достаточности капитала, базель 2, кредитный риск, срок до погашения, модель васичека, временная структура займа, показатель вероятности дефолта
Короткий адрес: https://sciup.org/147155909
IDR: 147155909 | УДК: 336.717
Текст научной статьи Влияние временной структуры портфеля на показатели минимального объема экономического капитала коммерческих банков и вероятности дефолта заемщиков
В последние годы произошло значительное усовершенствование методик измерения кредитного риска портфеля. Используемые в настоящее время модели, как правило, рассматривают стоимость портфеля на заданном горизонте времени, например, один год. Одной из наиболее распространенных является однофакторная модель Васи-чека [10]. Она легла в основу методологии определения уровня достаточности капитала, рекомендованной Базельским комитетом (BCBS, 2004) [2]. Согласно данному подходу, кредитный риск заключается только в возможности возникновения дефолтных событий. Модель предоставляет аналитическое решение для таких мер риска, как Value at Risk и Expected Loss. Одним из наименее изученных вопросов в этой области является влияние срока до погашения на кредитный риск портфеля. На практике принято считать, что риск растет с увеличением длительности займа, однако возможности рассмотрения различных сроков до погашения крайне редко обсуждаются.
Оценка кредитного риска является одной из основополагающих тем в области банков и финансов. Наибольшее количество существующих исследований направлено на развитие портфельных моделей и выявление распределения убытков по портфелю на заданном горизонте риска [12]. Благодаря этому существует возможность количественной оценки риска с помощью таких метрик, как Value at Risk (VaR) и Expected Loss (EL) или Unexpected Loss (UL=VaR – EL). В риск-ме-неджменте эти показатели используются для установления уровня резервов и экономического капитала, которые необходимы для защиты банка от возможных потерь, связанных с дефолтами заемщиков.
Большинство используемых моделей оценки риска кредитного портфеля сходятся во мнении, что стоимость портфеля является единственной наблюдаемой величиной. Стандартный временной горизонт принимается равным одному году (так же, как и в соглашении Базель 2) [2]. Очевидно, что этот временной горизонт в большинстве случаев не соответствует действительному сроку до погашения. Тем не менее, не существует работ, содержащих в себе подробного описания теоретического подхода и практической реализации, которые описывали бы возможное влияние временного горизонта и длительности займа на риск кредитного портфеля. Это утверждение справедливо и для модели, рекомендованной Базельским комитетом, несмотря на то, что формула для расчета капитала Базель 2 содержит поправку на срок до погашения для долгосрочных займов [3, 4].
Модель Васичека
Модель Васичека относится к классу структурных моделей [10, 11]. Она базируется на модели Мертона, изложенной в работе 1974 года. Данная модель нашла широкое применение в сфере оценки кредитных рисков и легла в основу ряда моделей, разработанных в более поздние годы. Наиболее известными из них являются Portfolio Manager™ и CreditMetrics™. Кроме того, модель Васичека стала одной из составляющих методологии Базель 2 для определения минимальных требований к капиталу на покрытие кредитного риска [2].
Согласно модели стоимость активов i -й компании описывается геометрическим броуновским движением. Логарифм стоимости активов компании в момент T имеет следующий вид:
( 02 )log (A( T )) = log (A) +I r —— I * T + 0* Tf * Zi, где Z – случайная величина, имеющая стандартное нормальное распределение.
Компания признается дефолтом, если рыночная стоимость ее активов падает ниже бухгалтерской стоимости долга. Таким образом, вероятность дефолта компании равна:
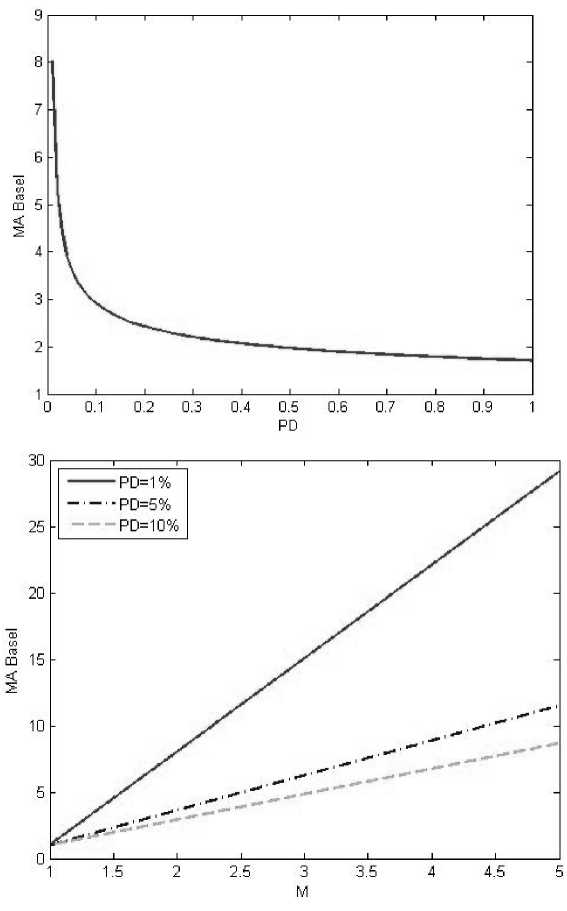
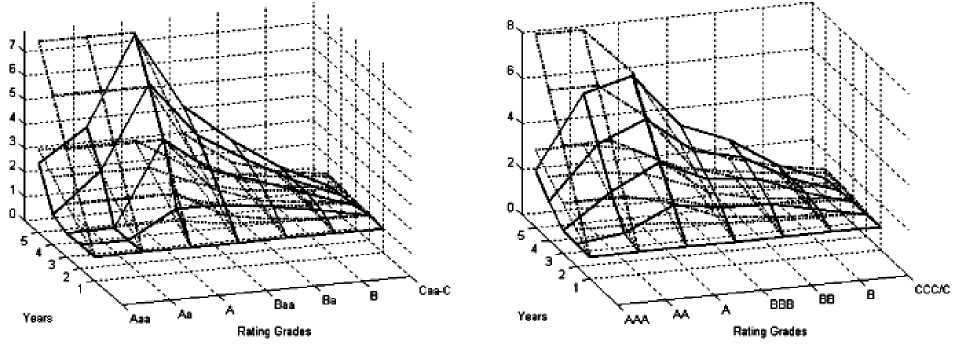
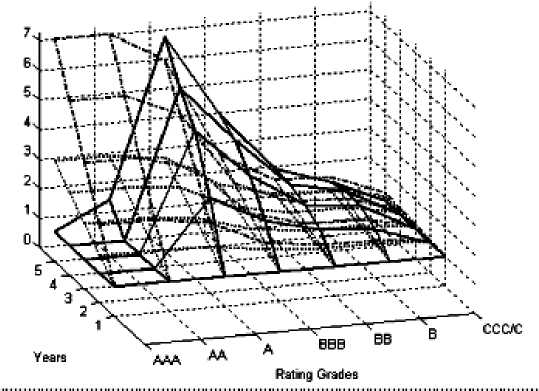
p = P[Att 1 (. 1 где ci = —^= * I log Ai- log Di + r * T — * о * T I, оTT к 2 ) N – функция нормального распределения. Так как zi имеют совместное стандартное нормальное распределение и равные попарные корреляции, zi могут быть представлены в следующем виде: zt = bx + aei,i = 1,2,...,n, где b = TP, a = Первое слагаемое характеризует влияние систематического риска, тогда как второе слагаемое – влияние идиосинкратического риска. В данном случае коэффициент b (0 < b < 1) показывает сте- пень подверженности заемщика систематическому риску (Vasicek, 1987). Рассмотрим портфель, состоящий из n одинаковых по сумме займов. Пусть вероятность дефол- та каждого из заемщиков по-прежнему равна p, а корреляция между стоимостями активов любых двух компаний равна ρ. При реализации фактора систематического риска x дефолты заемщиков происходят независимо. В этом случае каждое дефолтное событие может быть рассмотрено как результат испытания Бернулли. Тогда общее количество произошедших дефолтов при условии реализации x соответствует биномиальному распределению: Безусловная вероятность возникновения k дефолтов в портфеле может быть выражена следующим образом; Также в работе Васичека приводится функция распределения доли дефолтов в портфеле при условии бесконечно большого количества заемщиков (Vasicek, 1991): FM(6) = NI -(TI^PN-1 (6)-N-1 (p)) Именно на функции распределения доли дефолтов, предложенной Васичеком, основывается формула минимальных требований к капиталу Базель 2 на покрытие кредитных рисков [3]. Выразив, значение доли дефолтов мы получаем: 6 = N N-1 (p) + VPN-1 (FM(6))'V1-p , Для нахождения VaR кредитного портфеля при установленном Базельским комитетом уровне надежности 99,9 %: FM(6) = 0,999. Таким образом, θ представляет собой квантиль распределения доли заемщиков-дефолтов заданного уровня надежности. VaR = N (N-1(R) + RRN-1(0,999) ' 1 - R ) xLGD, где LGD (loss given default) – уровень потерь в случае дефолта; R – фактор корреляции. Экономическая теория и мировая экономика Поправка в виде штрафа на капитал (Maturity Adjustment) V Поправка на срок до погашения Базель 2 Кредитные портфели включают в себя инструменты с различными сроками до погашения. Интуитивно понятно, что долгосрочные займы являются более рискованными, чем краткосрочные. Вследствие этого капитальные требования должны увеличиваться с ростом длительности займа [9]. С целью учета данной особенности формула минимальных требований на капитал Базель 2 содержит поправку на срок до погашения (MA): K=[LGDхN 1-Rr х N-1(PD) + + -^— х N1(0,999) \1 - R ' ' - PD х LGD х MA. Известно, что вид данной корректировки был получен при использовании KMV Portfolio ManagerTM. Корректировка на срок до погашения представляет собой своеобразный фактор штрафа за превышения временного горизонта, равного одному году. Зависимость от длительности займа линейна для временных промежутков от одного до пяти лет и имеет следующий вид: MA = 1 + (M - 2,5)х b (PD) 1 -1,5 х b (PD) , где b (PD) = (0,11852 - 0,05478 * log (PD))2; PD -вероятность дефолта с временным горизонтом, равным одному году. На рис. 1 представлена зависимость величины поправки на капитал Базель 2 от одногодичной вероятности дефолта. Для высоких значений вероятности дефолта наблюдается более сильное влияния срока до погашения чем для низких вероятностей дефолта [9]. На рис. 2 мы можем видеть, что величина поправки на срок до погашения имеет прямую линейную зависимость от срока займа. Рис. 1. Зависимость поправки на срок до погашения Базель от вероятности дефолта при M = 2 Рис. 2. Зависимость поправки на срок до погашения Базель от срока займа (M) V Поправка на срок до погашения в рамках модели Васичека Теоретически в модели Васичека изменение срока до погашения займов в портфеле приводит к изменению вероятности дефолта в формуле условной вероятности дефолта. Поэтому рассмотрим, как преобразуется вероятность дефолта (PD(0, M)) при изменении срока до погашения (M). Сравним вероятность дефолта займа с длительностью t = T и M = m* T, где m > 1 . Вероятность дефолта при t = m*T приобретает следующий вид: PD(0,m*T) _ n 'N -1 (PD<0,T >) - 1 ---x—=---- - k *—j=^ m mm Очевидно, что параметры PD(0,T>, p могут быть найдены из однопериодной модели, а параметр m является заданным. Таким образом, для определения непредвиденных потерь необходимо оценить только параметр k. Альтернативный способ нахождения величи- l (m*T) где b PD<0, m *T > = N (b(m *T>), N-1(PD(0, T>) ны непредвиденных потерь заключается в нахождении UL на одногодичном временном промежутке и коррекции его с помощью функции, зависящей от m: m — i u. (T> - k * mJ-; и k = ^— . V m o(T> UL (l(0,m*T>) = UL (l(0,T>) * g (PD(0,T>, k, m, p); Таким образом, вероятность дефолта (0,m*T PD зависит от одногодичной вероятности дефолта PD(0,T> и параметра k, который может быть найден из доходности заемного капитала по-(t)x сле учета издержек (ц ') и ее стандартного от UL (l(0, m *T >) = N ' N-1(PD(0,m *T >)-VP* x(m *T >" PD(0, m *T > клонения (о( T>). Далее рассмотрим, как увеличение длительности займа влияет на вероятность дефолта при m > 1. PD(0,m*T>> pd(0,T><. N-1(PD(0, T>) - k * ' N-1(PD(0,T >)-VP* x(T > - PD(0, T > . m -1 * m > N-1 (PD(0,T>)<=> k < N-1(PD(0, T>) mm +1 Из этого следует, что вероятность дефолта PD(0,m*T>будет расти в сравнении с PD(0,T>, если k или PD(0,T>имеют низкие значения. Таким об В данном случае функция g представляет собой поправку на срок до погашения. Она может быть определена при известных параметрах PD(0,T>, k, m, p . Если значения параметров невозможно определить, то g аппроксимируется с помощью более простой функции. Многопериодные оценки вероятности банкротства и их влияние на величину экономического капитала разом, вероятность дефолта PD(0,m*T>будет увеличиваться более существенно для низких PD(0,T>чем для высоких. Этот эффект будет бо- лее заметен при рассмотрении непредвиденных потерь (UL), так как зависимость UL от PD имеет вогнутую форму. В данном случае непредвиденные потери могут быть выражены как: UL (l(0,m*T>) = VaR (l(0,m*T>) - E (l(0,m*T>), где VaR (l(0, m*T )) = N 'N-1(PD(0,m*T))-7P*x(m*T) ' E(l(0,m*T)) = pd(0,m*T) ■ Гюртлер и Хайфекер в своей работе 2005 года [5] анализировали влияние срока до погашения на капитал на основе долгосрочных вероятностей дефолта. Авторами были использованы эмпирические данные по статистике корпоративных дефолтов трех крупнейших рейтинговых агентств Moody’s, Standard and Poor’s и Fitch. В исследовании [5] была проведена: – оценка параметра k для нахождения влияния срока до погашения на капитал в рамках модели Васичека; – сравнение величины непредвиденных потерь, полученной на основе модели Васичека с соответствующими эмпирическими значениями непредвиденных потерь, найденными с помощью статистики дефолтов; – сравнение «модельной» поправки на срок до погашения и найденной при использовании эмпирических данных; Экономическая теория и мировая экономика – оценка упрощенной функции поправки на срок до погашения (g) аналогичной рекомендованной Базельским комитетом; – сравнение значений упрощенной функции поправки на срок до погашения со значениями, полученными на основе модели Васичека и с эмпирическими значениями поправки на капитал, полученными на основе данных рейтинговых агентств по дефолтам. Для оценки вероятности дефолта авторы использовали среднюю кумулятивную долю дефол- 0, m * T) тов DR ( , ) . На рис. 3 представлены поправки на срок до погашения (модельные значения, Базель 2, эмпирические) для различных рейтинговых разрядов. Легко заметить, что значение поправки на капитал, полученные на основе модели Васичека, переоценены по сравнению с эмпирическими в особенности для высоких рейтингов, однако хорошо соответствуют им при высоких значениях вероятности дефолта. Это вызвано тем, что для инвестиционных рейтингов непредвиденные потери имеют меньшее значение, в то время как для низких рейтингов – высокое. На основе полученных результатов исследователи [5] делают вывод о том, что оценки поправки на капитал по модели Васичека в большей мере приближаются к эмпирическим и значительно выше чем оценки, полученные при использовании формулы, рекомендованные в соглашении Базель 2. Моделирование корректировки величины экономического капитала в соответствии с рекомендациями Базель 2 В работе Помазанова М., Петрова Д. [9] была проведена непрерывная параметризация зависимости вероятности дефолта от времени на основе данных рейтингового агентства Moody’s. Кроме того, присутствует аналитический вывод полученных результатов. Временная структура вероятно- Moody’s Standard and Poor’s Fitch Рис. 3. Сравнение эмпирической поправки на срок до погашения (черным сверху), поправки на срок до погашения Базель 2 (светло-серым внизу) и поправки на срок до погашения, полученной на основе модели Васичека (серым посередине) сти дефолта делает возможным нахождение величины поправки на срок до погашения. Подход, использованный авторами, делает более объясни- мым и «прозрачным» процесс расчета поправки на срок до погашения. В ходе работы исследователями была проведена аппроксимация кумулятивных вероятностей дефолтов для каждого рейтингового разряда с помощью следующей функции: PDT = F (PDn, a, b, T ) = PDn | 1 - exp (-T • a) 100 ^ 1 - exp (-a) l[ 1 - exp (-T • a) ] [ 1 - exp (-T • b) ]l +1 - rx |l 1 - exp (-a) J ^ 1 - exp (- b) JI . r1- exp(- b)) x [ 100 J _ Данный вид функции был выбран на основе ряда свойств вероятности дефолта, а именно: 1) для срока погашения, равного одному году, PDn должна соответствовать одногодичной вероятности дефолта; 2) при нулевом сроке до погашения вероятность дефолта также равна нулю; 3) функция имеет асимптоту для высоких значений, которая не равна 100 %. Это свойство следует из того, что с течением времени компании либо сравнительно быстро становятся дефолтами, либо достигают более высокого рейтинга. Таким образом, присутствует некоторая степень стабилизации. Свойство выполняется, если параметр a больше b для каждого рейтингового разряда; 4) при низких значениях вероятности дефолта функция вогнута, при высоких – выпукла. Данное свойство следует из того, что компании с высоким рейтингом, как правило, проходят несколько более низких рейтинговых разрядов прежде, чем стать дефолтами. Поэтому возникает некоторый период, в который кумулятивные вероятности дефолта не имеют быстрого роста (вогнутость). Компании с низким рейтингом, напротив, становятся дефолтами сравнительно быстро, поэтому мы не можем наблюдать схожего эффекта: кумулятивная вероятность дефолта стремительно растет (выпуклость). Результаты, полученные авторами [9], свидетельствуют о том, что при использовании функции поправки на срок до погашения Базель 2 происходит недооценка риска. В исследовании выявлено, что эффект срока до погашения на капитал значительно более существенен для инвестиционных рейтингов со сроком до погашения, приблизительно равным двум годам. Петров и Помазанов подчеркивают, что оценка величины непредвиденных потерь является важнейшим этапом для достижения стабильности банка. Рекомендации Базель 2, которые принято считать консервативными, допускают недооценку риска, которая в некоторых случаях превосходит 50 %. Заключение В проведенном исследовании рассмотрена одна из наиболее распространенных моделей кредитного риска портфеля – модель Васичека, приведен аналитический вывод поправки капитала на срок до погашения и основные свойства, которыми должна обладать данная функция. Кроме того, проведен обзор существующих подходов, посвященных анализу влияния на капитал срока до погашения. На основе проведенного анализа сформирован вывод о том, что использование формулы поправки на капитал, рекомендованной в соглашении Базель 2, может привести к значительной недооценке риска, в особенности для высоких рейтингов. Более того, остаются неизвестными подробности происхождения и вывода формулы поправки на срок до погашения, предлагаемой Базельским комитетом. Также проведенные исследования показали, что отсутствует и ее практическое подтверждение.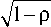
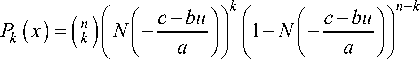
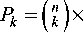
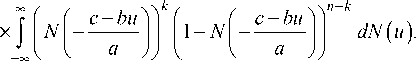
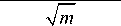
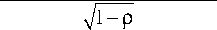
Список литературы Влияние временной структуры портфеля на показатели минимального объема экономического капитала коммерческих банков и вероятности дефолта заемщиков
- Barco, M. Bringing Credit Portfolio Modelling to Maturity/M. Barco//Risk 17. -2004. -V. 1. -P. 86-90.
- Basel Committee on Banking Supervision. International Convergence of Capital Measurement and Capital Standards, Bank for International Settlements. 2004. -http://www.bis.org/publ/bcbs107.htê
- Basel Committee on Banking Supervision. An Explanatory Note on the Basel II IRB Risk Weight Function, Bank for International Settlements. 2005. -http://www.bis.org/bcbs/irbriskweight.htê
- Bluhm, C., and Overbeck, L. Systeêatic Risk in Homogeneous Credit Portfolios. Credit risk: Mea-sureêent, Evaluation and Management, Heidelberg. 2003. -http://www.uni-giessen.de/~gc1156/papers/rsquared.pdf
- Grundke, P. The Terê Structure of Credit Spreads as a Determinant of the Maturity Effect on Credit Risk Capital/P. Grundke//Finance Letters 1. -2003. -V. 6. -P. 4-9.
- Gurtler, M., and Heithecker, D. Multi-Period defaults and êaturity effects oneconoêic capital in a ratings-based default-mode model/M. Gurtler, D. Heithecker//Finanz Wirtschaft Working Paper. Braunschweig University of Technology Institute for Economics and Business Administration Departêent of Finance. -Series FW19V2/05. -2005.
- Kalkbrener, M., and Overbeck, L. Maturity as a factor for credit risk capital, Technical document, CIB/CRM/RAI Risk Research & Development, Deutsche Bank, Frankfurt.-2001.
- Kalkbrener, M., and Overbeck, L. The maturity effect on credit risk capital/M. Kalkbrener, L. Overbeck//Risk 14. -2005. -V. 7. -P. 59-63.
- Petrov, D., Pomazanov, M. Validation of maturity model validation. -2009. -V. 3, № 3. -P. 1-17.
- Vasicek, O. A. Probability of Loss on Loan Portfolio. KMV Corporation. -1987. -http://www.Éoodysanalytics.com/~/media/Insight/Qua ntitative-Research/Portfolio-Modeling/87-12-02-Probability-of-Loss-on-Loan-Portfolio.ashx
- Vasicek, O. A. Limiting Loan Loss Probability Distribution. KMV Corporation. -1991. -http://www.moodysanalytics.com/~/media/Insight/Qua ntitative-Research/Portfolio-Modeling/91-08-09-Limiting-Loan-Loss-Probability-Distribution.ashx
- Vasicek, O.A. Loan Portfolio Value/O. Vasicek//Risk 15. -2002. -V. 17. -P. 160-162.


