Влияние жесткости фундамента на напряженно-деформированное состояние каменно-бетонной плотины с бетонным покрытием

Каменно-набросные плотины с бетонным экраном (КНПБЭ) являются перспективным типом грунтовых плотин, т.к. они могут применяться в самых разнообразных природных условиях. Эти плотины применяются в гидротехническом строительстве с конца XIX века и за прошедшее время область их применения значительно расширилась, максимальная высота построенных плотин превысила 200 м [1].

Однако на протяжении всей истории применения КНПБЭ требовалось решение проблемы обеспечения надёжности противофильтрационного бетонного экрана (БЭ). В первой половине XX в., когда высота КНПБЭ превысили 100 м, эта проблема встала особенно остро. Образование трещин фиксировалось в экранах плотин Salt Springs (1931), Cogswell (1935) [1]. Для обеспечения трещиностойкости БЭ конструкции КНПБЭ постоянно совершенствовались, однако проблема Sainov, M.P.; Soroka V.В.

Impact of foundation stiffness on the stress-strain state of the concrete face of a rockfill dam;

надёжности БЭ сохраняет свою актуальность до сих пор. Даже у современных КНПБЭ имеются случаи нарушения целостности бетонного экрана [2,3]. Примерами могут служить сверхвысокие плотины Aguamilpa [2], Tianshengqiao 1 [2, 4], Turimiquire [7], Barra Grande [2,6], Mohale [4,5], Саmpos Novos [2,4,8].

Опыт свидетельствует о том, что определяющим фактором надёжности жёсткого бетонного экрана являются деформации самой грунтовой плотины. Чем они больше, тем выше опасность повреждения экрана. Поэтому при строительстве высоких КНПБЭ стремятся максимально снизить деформируемость каменной наброски. В современных плотинах каменную наброски уплотняют столь тщательно, что модуль деформации каменной наброски может достигать 400÷500 МПа.

Однако деформации КНПБЭ определяются не только деформируемостью каменной наброски тела плотины, но и деформируемостью грунтов основания. Между тем, иногда основанием КНПБЭ являются нескальные отложения, которые могут иметь существенно большую сжимаемость, чем каменная наброска. В частности, самая высокая в мире КНПБЭ Shuibuya (Китай) [9] построена на слое аллювиальных песчано-гравийных грунтов толщиной около 20 м. Для повышения надёжности плотины часть отложений была удалена, а другая часть – уплотнена. При большей толщине отложений их выемка экономически не выгодна, поэтому их сохраняют.

Можно привести несколько примеров строительства высоких КНПБЭ на мощном слое нескальных отложений. Информация о них приведена в [10, 11]. Первой такой плотиной можно считать плотину Alto Anchicaya высотой 154 м. Она была возведена в 1983 г. в Колумбии на слое песка и гравия толщиной 34 м. В XXI веке был построен целый ряд КНПБЭ плотин на нескальном основании. При их перечислении укажем их высоту H и толщину слоя нескальных отложений T. Это плотины Dhauliganga (2006, Индия, H=56 м, T=70 м), Aertash (Турция, H=164,8 м, T=94 м) [11], Limon (Чили, H=82 м, T=46 м) [12], Nalan (2005, Китай, H=109 м, T=24 м) [13], Jiudianxia (2008, Китай, H=136,5 м, T=56 м) [14], Chahanwusu (2009, Китай, H=107,6 м, T=47 м) [15], Miaojiaba (2011, Китай, H=111 м, T=48 м) [16,17].

В связи распространением КНПБЭ на сжимаемом основании актуальным и важным вопросом является исследование влияния деформируемости основания на напряжённо-деформированное состояние (НДС) КНПБЭ. Рядом исследователей выполнены публикации, посвящённые изучению этого вопроса. Работа [10] посвящена сравнению результатов натурных измерений перемещений КНПБЭ на скальном и нескальном основании.

Публикации [16-18] посвящены численному моделированию НДС КНПБЭ, расположенных на нескальном основании. Однако в публикациях в основном анализируются лишь деформации и устойчивость плотины [18]. Более обстоятельные исследования были выполнены в Китае, они посвящены расчётному обоснованию плотины Miaojiaba [16,17]. Но в этих работах было проанализировано напряжённое состояние только ПФС, а прочность БЭ не оценивалась.

Поэтому вопрос о НДС БЭ плотины на нескальном основании остаётся не изученным. Чтобы восполнить этот пробел, нами были выполнено методическое исследование по выявлению влияния свойств основания на НДС экрана.

2    Materials and Methods

Исследование НДС КНПБЭ проводилось путём численного моделирования. Расчёты НДС проводились на нагрузки основного сочетания, от собственного веса материалов и гидростатического давления.

Рассматривалась абстрактная КНПБЭ высотой 100 м, расположенная на слое нескального основания толщиной 100 м (рис.1). По опыту большинства строительства плотин на нескальном основании [11-17] принималось, что основание может быть изолировано от верхнего бьефа путём устройства глубокой противофильтрационной стены (ПФС). Сопряжение стены и бетонного экрана осуществляется с помощью бетонного понура. Благодаря понуру ПФС отстоит от тела плотины на 10 м в сторону верхнего бьефа. Такая схема сопряжения БЭ и ПФС является общепринятой и, в частности, применена в конструкциях плотин Aertash [11] и Miaojiaba [17].

Строение тела плотины принималось неоднородным. Принималось, что основной объём плотины выполнен из сортированной каменной наброски (горная масса) и уплотнён более тщательно, чем несортированная наброска в низовой части (рис.1).

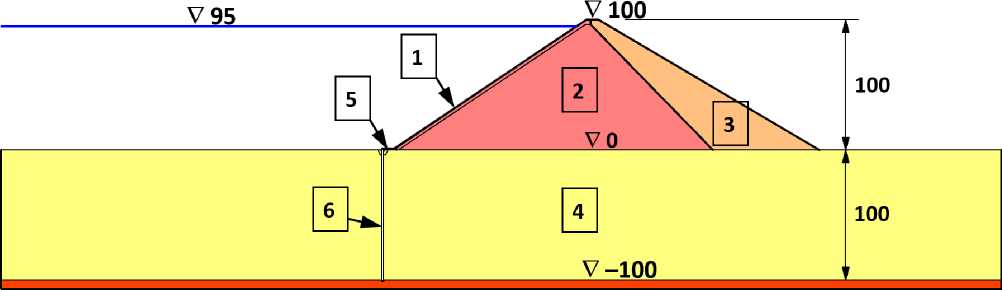
Рис.1 - Схема строения каменно-набросной плотины с бетонным экраном, расположенным на мощном слое основания

Fig.1 - Diagram of the structure of a concrete faced rockfill dam a located on a thick base layer

• 1    – бетонный экран; 2 и 3 – верховая и низовая части упорной призмы каменно-набросной плотины; 4 – слой основания; 5 – бетонный понур; 6 – противофильтрационная стена в основании.

Принималось, что экран укладывается на подэкрановую зону из грунта, без устройства подготовки из малоцементного бетона. Данный случай является более опасным, т.к. не предусматривает осуществления мероприятий по снижению трения между экраном и телом плотины.

Для выявления роли жёсткости основания в формировании НДС КНПБЭ рассматривались несколько расчётных схем:

схема 1 – плотина расположена на абсолютно жёстком основании;

схема 2 – плотина расположена на водонепроницаемом основании конечной жёсткости, в котором противофильтрационная стена не выполняется;

схема 3 – плотина расположена на водопроницаемом основании конечной жёсткости, для предотвращения фильтрации в котором выполнена ПФС (рис.1).

Схемы 2 и 3 различаются не только наличием стены, но и воспринимаемыми нагрузками. В схеме 3 на противофильтрационную стену действует гидростатическое давление верхнего и нижнего бьефов. Рассмотрение схем 2 и 3 необходимо для того, чтобы оценить роль в изменениях НДС каждого из двух факторов – жёсткости основания и схемы приложения нагрузок на стену.

Все материалы расчётной схемы принималась линейно деформируемыми, однако материалы ПФС и БЭ рассматривались как упругие. При моделировании грунтов учитывалась возможность потери прочности на сдвиг и растяжение. Для оценки сопротивления сдвигу использовалась модель Кулона-Мора. В некоторых случаях, для возможности сравнения были проведены расчёты с упругим поведением грунтов.

Расчёты НДС проводились для двух вариантов деформируемости каменной наброски (горной массы). В одном варианте (вариант A) модуль линейной деформации каменной наброски E к верховой части плотины принимался равным 120 МПа, а во втором (вариант B) – 480 МПа. В обоих вариантах коэффициент Пуассона каменной наброски ν к принимался равным 0,2. Модуль линейной деформации каменной наброски низовой части призмы принимался в 2 раза меньше, чем в верховой (E к ). Угол внутреннего трения каменной наброски принимался переменным: от 53 º (при нулевых напряжениях σ ) до 36 º (при σ =1 МПа).

Расчёты по схемам 2 и 3 проводились для широкого диапазона типов грунтов основания, и соответственно его жёсткости. Известно, что грунты нескального основания плотины Aertash имеют модуль деформации 40÷55 МПа [11]. В наших расчётах модуль линейной деформации грунта основания E о варьировался от 40 МПа до 20 ГПа, т.е. от нескального до скального. Таким образом, в части вариантов плотина располагалось на «мягком» основании по сравнению с каменной наброской, а в части – на жёстком. Всего было рассмотрено 22 варианта (табл.1). В таблице указаны также прочностные показатели грунта основания (угол внутреннего трения ϕ о и удельное сцепление с о ).

Материал стены назначался в зависимости от деформируемости грунтов основания. Принималось, что модуль деформации материала стены должен не более, чем в 5 раз выше, чем модуль деформации грунта основания (табл.1). Таким образом, материалом стены мог быть литой глиноцементобетон, пластичный и обычный бетоны.

Таблица 1. Параметры расчётных вариантов

Table 1. Parameters of design variants

Номер вар.	Тип схемы	Плотина	Основание				ПФС
		E к [МПа]	E о [МПа]	ν о	ϕ о	с о [кПа]	E c [МПа]	ν c
1.A	абсолютно жёсткое основание	120	–	–	–	–	–	–
1.B	абсолютно жёсткое основание	480	–	–	–	–	–	–
2.A.a	основание без стены	120	40	0.33	38	0	200	0.33
2.A.b	основание без стены	120	200	0.33	40	0	1000	0.30
2.A.c	основание без стены	120	1000	0.33	30	30	5000	0.25
2.A.d	основание без стены	120	5000	0.25	33	50	29000	0.20
2.A.e	основание без стены	120	20000	0.25	35	100	29000	0.20
2.B.a	основание без стены	480	40	0.33	38	0	200	0.33
2.B.b	основание без стены	480	200	0.33	40	0	1000	0.30
2.B.c	основание без стены	480	1000	0.33	30	30	5000	0.25
2.B.d	основание без стены	480	5000	0.25	33	50	29000	0.20
2.B.e	основание без стены	480	20000	0.25	35	100	29000	0.20
3.A.a	основание со стеной	120	40	0.33	38	0	200	0.33
3.A.b	основание со стеной	120	200	0.33	40	0	1000	0.30
3.A.c	основание со стеной	120	1000	0.33	30	30	5000	0.25
3.A.d	основание со стеной	120	5000	0.25	33	50	29000	0.20
3.A.e	основание со стеной	120	20000	0.25	35	100	29000	0.20
3.B.a	основание со стеной	480	40	0.33	38	0	200	0.33
3.B.b	основание со стеной	480	200	0.33	40	0	1000	0.30
3.B.c	основание со стеной	480	1000	0.33	30	30	5000	0.25
3.B.d	основание со стеной	480	5000	0.25	33	50	29000	0.20
3.B.e	основание со стеной	480	20000	0.25	35	100	29000	0.20

Расчёты НДС проводись с учётом последовательности возведения плотины и наполнения водохранилища. Принималась следующая схема поэтапности. На первом этапе моделировалось формирование НДС основания, а далее – устройство в нём ПФС. В течение 15 последующих этапов моделировалось послойная отсыпка плотины горизонтальными слоями. Только после этого «укладывался» экран на полную высоту. Далее воспроизводилось постепенное наполнение водохранилища с ростом гидростатического давления на верховую грань экрана, понура и стены

Расчёты НДС проводились методом конечных элементов. Плотина и основание были разделены на 1220 конечных элементов сплошной среды. Возможность проявления нелинейных эффектов на контактах БЭ, понура с грунтами и между собой моделировалась с помощью 76 контактных конечных элементов.

Численное моделирование НДС КНПБЭ выполнялись с помощью вычислительной программы Nds_N, созданной Саиновым М.П.1 Она позволяет учитывать нелинейность деформирования, контактного взаимодействия и последовательность возведения плотины. Важным преимуществом является возможность использования конечных элементов высокого порядка для обеспечения адекватных результатов численного моделирования. Использовались конечные элементы с кубической степенью аппроксимацией перемещений внутри элемента. В каждом из конечных элементов сплошной среды напряжения фиксировались в 25 точках интегрирования. Общее количество степеней свободы конечно-элементной модели составило 11852.

3    Results and Discussion

Анализ влияния жёсткости основания на НДС плотины выполнялся для момента завершения наполнения водохранилища до уровня 95 м. Анализ проводился по следующим величинам: перемещения плотины и основания, перемещения напорной грани экрана и ПФС, напряжения в теле плотины и основании, напряжения на верховой и низовой гранях БЭ. Распределение их величин показано на рис.2-12, а максимальные величины – в табл.2.

Анализ перемещений плотины и основания.

Перемещения расчётной области за строительный период для разных вариантов показаны на рис.2 (осадки U y ) и рис.3 (горизонтальные смещения U x ). В них не учитываются перемещения основания при восприятии собственного веса.

Очевидно, что величины перемещений складываются из перемещений основания и перемещений тела самой плотины. Они находятся в обратной зависимости от модуля деформации основания E о и модуля деформации каменной наброски E к . Чем меньше модуль деформации основания, тем больше перемещения плотины (табл.2).

Таблица 2. Параметры НДС плотины для расчётных вариантов Table 2. Stress-strain state parameters of the dam for design variants

Номер варианта	Плотина	Основание	НДС плотины		НДС бетонного экрана
	E к [МПа]	E о [МПа]	U x [см]	U y [см]	U x [см]	U y [см]	U n [см]	max σ п [МПа]	min σ п [МПа]
1.A	120	–	16.0	36.2	14.1	14.1	19.6	5.5	-3.1
1.B	480	–	3.9	9.0	3.6	3.5	5.0	1.7	-1.9
2.A.a	120	40	122	331	93.8	116.8	149.2	7.3	-12.6
2.A.b	120	200	32	76	29.7	31.0	42.2	1.9	-5.3
2.A.c	120	1000	19.3	41	17.2	17.2	23.8	3.2	-3.8
2.A.d	120	5000	16.6	37.3	14.6	14.9	20.5	3.2	-3.4
2.A.e	120	20000	16.2	36.5	14.1	14.3	19.8	3.3	-3.2
2.B.a	480	40	135	326	81.7	110.0	136.9	9.6	-18.6
2.B.b	480	200	22	64	18.8	22.7	29.3	1.9	-5.3
2.B.c	480	1000	7.2	16.5	6.7	6.9	9.4	0.7	-3.0
2.B.d	480	5000	4.6	10.4	4.2	4.3	5.9	1.4	-2.3
2.B.e	480	20000	4.1	9.4	3.7	3.7	5.2	1.6	-2.0
3.A.a	120	40	179	311	179.6	105.2	188.4	0.8	-16.8
3.A.b	120	200	49	72	48.5	25.0	47.6	0.8	-9.9
3.A.c	120	1000	23.4	41	21.7	15.6	25.0	1.7	-5.3
3.A.d	120	5000	17.8	37	15.9	14.5	20.9	4.2	-3.8
3.A.d	120	20000	17.8	37	14.5	14.2	19.9	3.4	-3.4
3.B.a	480	40	186	309	156.7	103.2	172.7	4.9	-11.8
3.B.b	480	200	36	61	35.7	19.7	36.2	0.4	-9.5
3.B.c	480	1000	10.8	15.8	10.9	5.6	10.6	0.1	-5.8
3.B.d	480	5000	5.6	10.2	5.3	4.0	6.2	0.5	-3.3
3.B.e	480	20000	4.4	9.3	4.2	3.6	5.3	1.4	-2.3

Однако от модуля деформации основания зависят не только величины перемещений, но и характер их распределения.

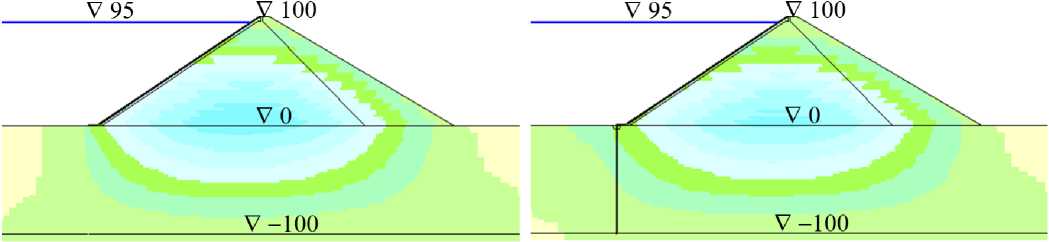
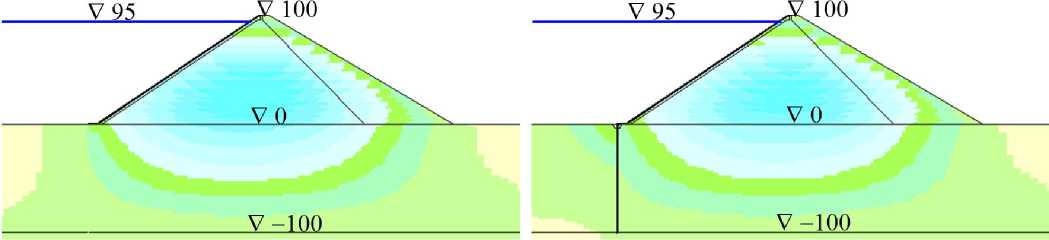
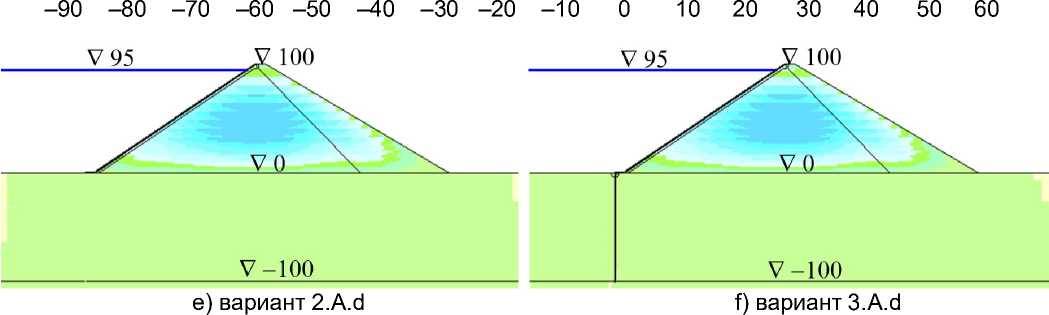
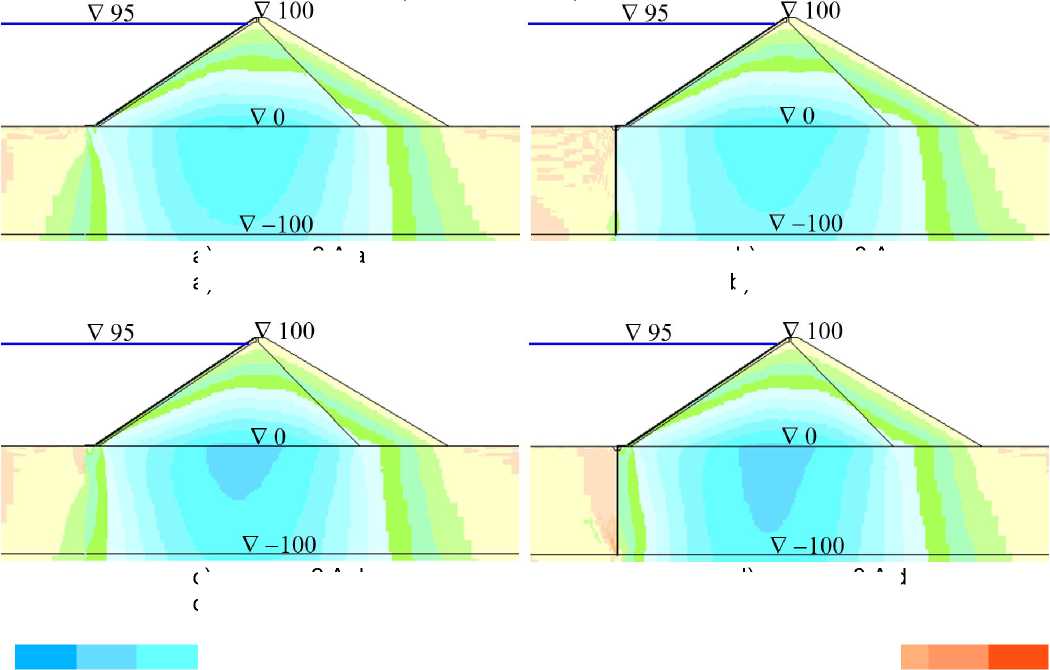
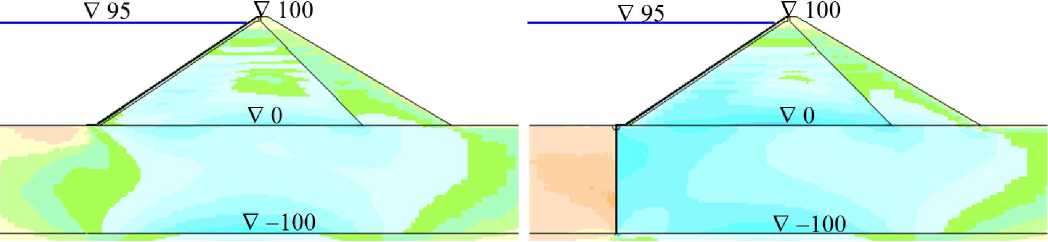
На рис.2 показано распределение осадок U y расчётной области (для вариантов серии A, E к =120 МПа). Из него видно, что в варианте №a (E о =40 МПа), в котором основание более деформируемо, чем тело плотины, зона максимальных строительных осадок располагается на подошве плотины (рис.2,a,b). В вариантах №с (E о =5 ГПа) и №d (E о =20 ГПа), в которых основание намного жёстче тела плотины, зона максимальных осадок расположена в центре тела плотины (рис.2,e,f). В варианте №b (E о =200 МПа) она занимает промежуточное положение (рис.2,c,d).

Рис.2 показывает, что устройство ПФС мало сказывается на величины и распределение осадок расчётной области. Основание интенсивно оседает только непосредственно под телом плотины, а в зоне расположения ПФС величины гораздо меньше максимальных.

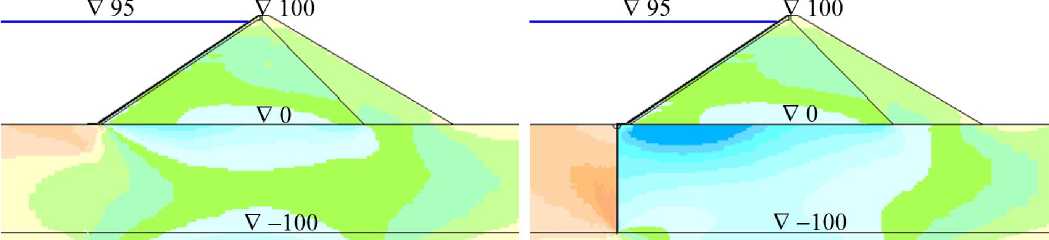
На рис.3 показано распределение горизонтальных смещений U x расчётной области (для вариантов серии A, E к =120 МПа). В большинстве вариантов максимальные смещения наблюдаются на напорной грани плотины. Только в варианте №a («мягкое» основание) зона высоких горизонтальных смещений располагается также на границе плотины и основания (рис.3,a,b).

a) вариант 2.A.a

a) variant 2.A.a

b) вариант 3.A.a

b) variant 3.A.a

шкала осадок U y [см]

–450 –400 –350 –300 –250 –200 –150 –100 –50   0

50  100  150  200 250  300

c) вариант 2.A.b

c) variant 2.A.b

d) вариант 3.A.b

d) variant 3.A.b

шкала осадок U y [см]

e) variant 2.A.d

f) variant 3.A.d шкала осадок Uy [см]

–36  –32  –28  –24 –20 –16  –12  –8   –4   0

4    8   12   16   20  25

Рис.2 - Распределение осадок расчётной области в различных вариантах при E к =120 МПа

Fig.2 - Distribution of settlement of the calculated area in different variants at E к =120 MPa

• a, b – при E о =40 МПа; c, d – при E о =200 МПа; e, f – при E о =5000 МПа;

• a, c, e – схема 2 (при отсутствии стены); b, d, f – схема 3 (при устройстве стены)

• a, b – at E о = 40 MPa; c, d – at E о = 200 MPa; e, f – at E о = 5000 MPa; a, c, e – scheme 2 (in the absence

of a seepage-control wall); b, d, f - scheme 3 (when constructing a seepage-control wall)

Sainov, M.P.; Soroka V.В.

Impact of foundation stiffness on the stress-strain state of the concrete face of a rockfill dam;

Расчёты показали, что на величины и характер распределения горизонтальных смещений большое влияние оказывает устройство ПФС в основании. Под действием гидростатического давления ПФС получает существенные смещения, которые увеличивают общие смещения расчётной области (рис.3,b,d,f).

Смещения ПФС оказывают некоторое влияние и на осадки. Для схемы №3, предусматривающей устройство ПФС, характерно некоторое повышение осадок основания с верховой стороны от стены (рис.2d).

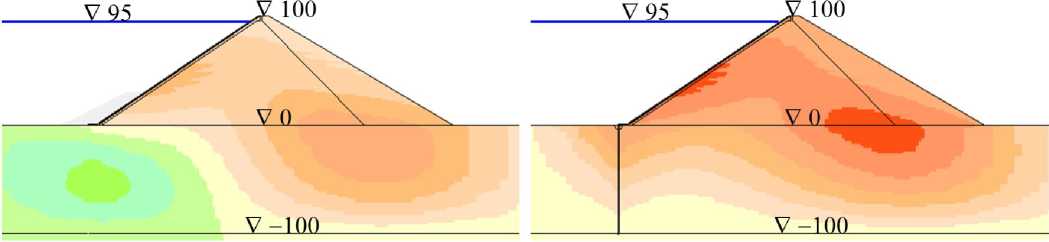
a) вариант 2.A.a                                 b) вариант 3.A.a

a) variant 2.A.a                                      b) variant 3.A.a шкала горизонтальных смещений Uy [см]

–225 –200 –175 –150 –125 –100 –75 –50 –25   0   25  50   75  100  125 150

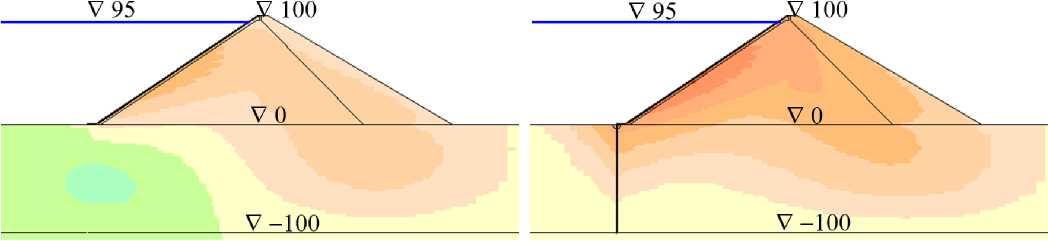
c) вариант 2.A.b                                 d) вариант 3.A.b

c) variant 2.A.b                                      d) variant 3.A.b шкала горизонтальных смещений Uy [см]

–72  –64  –56  –48 –40  –32  –24 –16  –8   0    8   16  24   32   40  48

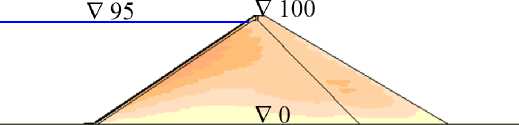
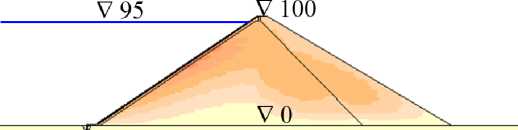
V-100

• e) вариант 2.A.d

• e) variant 2.A.d

  V-100

  f) вариант 3.A.d

  f) variant 3.A.d

  
  

шкала горизонтальных смещений U y [см]

–27  –24  –21  –18 –15  –12  –9  –6   –3   0    3   6    9   12   15   18

Рис.3 - Распределение горизонтальных смещений расчётной области в различных вариантах при E к =120 МПа

Fig. 3 - Distribution of horizontal displacements of the computational area in different versions at E k =120 MPa

• a, b – при E о =40 МПа; c, d – при E о =200 МПа; e, f – при E о =5000 МПа;

• a, c, e – схема 2 (при отсутствии стены); b, d, f – схема 3 (при устройстве стены)

• a, b – at E о = 40 MPa; c, d – at E о = 200 MPa; e, f – at E о = 5000 MPa; a, c, e – scheme 2 (in the absence of a seepage-control wall); b, d, f - scheme 3 (when constructing a seepage-control wall)

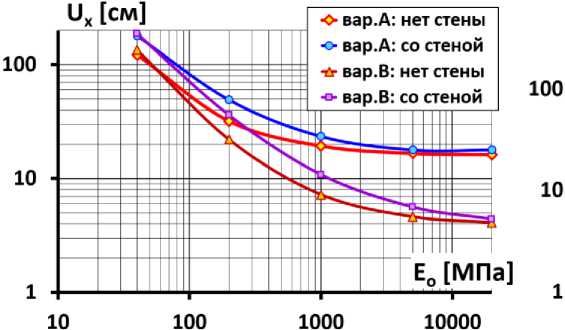
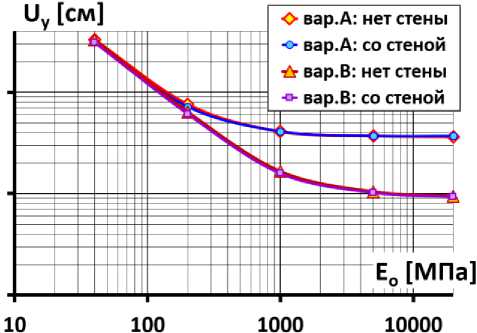
Анализ изменения максимальных величин смещений и осадок позволяет выполнить табл.2 и рис.4. Они показывают влияние модуля деформации основания и плотины на величины перемещений.

• a) смещения b) осадки a) displacement b) settlement

Рис.4 - Изменение максимальных перемещений плотины в зависимости от модуля деформации основания

Fig. 4 - Change in maximum dam displacements depending on the base deformation modulus

Видно, что при E о <200 МПа, т.е. при «мягком» основании, максимальные осадки практически не зависят от деформируемости плотины (варианты серии « a » ). Наоборот, при E о >5000 МПа – смещения не зависят от деформируемости основания (рис.4b). Наличие ПФС практически не сказывается на максимальные величины осадок (рис.4b).

На величины горизонтальных смещений оказывают влияние все три фактора: жёсткость основания, деформируемость плотины и наличие ПФС (рис.4a). Основным определяющим фактором является жёсткость основания. При жёстком основании (при E о >5000 МПа) на перемещения практически не сказывается наличие ПФС и модуль деформации основания.

Тем не менее, можно отметить, что перемещения плотины в схеме №1 (абсолютно жёсткое основание) несколько меньше, чем перемещения при самом жёстком из рассмотренных оснований.

Анализ напряжений в плотине и основании.

Анализ напряжений в теле плотины и основании позволяют провести рис.5 и 6, на которых показано распределение осевых нормальных напряжений σ y и σ x . Представленные на рисунках напряжения не учитывают напряжения от собственного веса основания.

Из рис.5 видно, что характер распределения вертикальных напряжений σ y мало зависит от деформативных свойств основания. Сжимающие напряжения σ y равномерно увеличиваются от гребня к подошве плотины. С верховой стороны напряжения σ y несколько выше, чем с низовой, за счёт гидростатического давления на экран. В основании сжимающие напряжения практически не изменяются с глубиной.

В зоне устройства ПФС напряжения σ y относительно не велики. Однако при устройстве ПФС напряжения σ y в этой зоне распределяются иначе (рис.5,a,c). С низовой стороны от стены уровень сжатия несколько увеличивается, а с верховой – напряжения σ y падают практически до 0 (рис.5,b,d).

Напротив, величина и характер распределения горизонтальных напряжений σ x сильно зависят от соотношения деформируемости основания и тела плотины, а также от устройства ПФС (рис.6).

В вариантах, в которых модули деформации основания и плотины существенно отличаются друг от друга, напряжения σ x в теле плотины и в основании значительно различаются по величине. Особенно это заметно в зоне подошвы плотины.

При E о >>E к (жёсткое основание) в верхней части основания возникает зона концентрации сжимающих напряжений σ x (рис.6,c,d). Они могут существенно превышать 1 МПа (рис.6,d). При этом в теле плотины сжимающие напряжения σ x не превышают 0,5 МПа.

b) вариант 3.A.a

b) variant 3.A.a шкала вертикальных напряжений σy [МПа]

–2,0 –1,8 –1,6 –1,4 –1,2 –1,0 –0,8 –0,6 –0,4 –0,2

c) вариант 2.A.d

c) variant 2.A.d

d) вариант 3.A.d

d) variant 3.A.d

0    0,2   0,4  0,6   0,8   1,2

Рис.5 - Распределение вертикальных напряжений в различных вариантах при E к =120 МПа

Fig.5 - Distribution of vertical stresses in different variants at E k = 120 MPa

a) вариант 2.A.a

• a) variant 2.A.a

  • a, b – при E о =40 МПа; c, d – при E о =5000 МПа;

• a, c – схема 2 (при отсутствии стены); b, d – схема 3 (при устройстве стены)

• a, b – at E о = 40 MPa; c, d – at E о = 5000 MPa;

• a, c – scheme 2 (in the absence of a seepage-control wall); b, d – scheme 3 (when constructing a seepage-control wall)

При E о к (мягкое основание) у подошвы плотины возникает зона разуплотнения грунтов плотины, т.к. под весом плотины основание «расползается» в стороны. Расчёты для упругого поведения грунтов показало наличие в этой зоне высоких растягивающих напряжений σ x . Это характерно для вариантов A.а, B.a, B.b. В них E к /E о >3.

Благодаря ослаблению грунта плотины в этих вариантах высокие горизонтальные смещения плотины приводят к повышению уровня сжаимающих σ x , особенно в приконтактной области (рис.6,a,b).

При устройстве ПФС в основании уровень сжимающих напряжений σ x в теле плотины и в основании с низовой стороны возрастает (рис.6,b,d). Особенно существенно напряжения σ x возрастают в зонах концентрации (рис.6,d). С верховой стороны от стены происходит уменьшение сжатия по σ x .

Анализ перемещений бетонного экрана.

Влияние жёсткости основания, а также устройства ПФС на величины и характер распределения перемещений экрана позволяет провести анализ рис.7-9 и табл.2, в которых показаны перемещения напорной грани бетонного экрана плотины. Это горизонтальные смещения U x (рис.7), осадки U n (рис.8), а также прогибы U n , т.е. перемещения экрана в направлении поперёк к поверхности верхового откоса.

Анализ показал, что для жёсткого основания (варианты серий « c », « d » ) характерно неравномерное распределение перемещений экрана по высоте (рис.7-9). Оно свидетельствует о деформациях поперечного изгиба экрана. Практически по всей своей высоте экран выгибается в сторону нижнего бьефа, за исключением самой верхней части.

c) вариант 2.A.d                                 d) вариант 3.A.d

c) variant 2.A.d                                       d) variant 3.A.d шкала горизонтальных напряжений σx [МПа]

a) вариант 2.A.a                                 b) вариант 3.A.a

a) variant 2.A.a                                      b) variant 3.A.a

–1,0 –0,9 –0,8 –0,7 –0,6 –0,5 –0,4 –0,2 –0,1    0   0,1  0,2   0,3  0,4   0,5   0,6

Рис.6 - Распределение горизонтальных напряжений в различных вариантах при E к =120 МПа

Fig.6 - Distribution of horizontal stresses in different variants at E k =120 MPa

• a, b – при E о =40 МПа; c, d – при E о =5000 МПа;

• a, c – схема 2 (при отсутствии стены); b, d – схема 3 (при устройстве стены)

• a, b – at E о = 40 MPa; c, d – at E о = 5000 MPa;

• a, c – scheme 2 (in the absence of a seepage-control wall); b, d – scheme 3 (when constructing a seepage-control wall)

Уменьшение жёсткости (модуля деформации) основания проводит к увеличению величин перемещений экрана, а также к их перераспределению по высоте.

Влияние устройства ПФС на перемещения экрана также выражается в дополнительном увеличении их величин. При этом оно сопровождается уменьшением неравномерности их распределения по высоте, т.е. уменьшением деформаций поперечного изгиба.

Таким образом, уменьшение жёсткости и устройство ПФС не просто изменяет величины перемещений экрана, но и изменяет характер деформаций его поперечного изгиба.

Для более детальной оценки влияния жёсткости основания и устройства ПФС на перемещения экрана необходимо провести анализ по отдельным компонентам перемещений экрана.

Сначала рассмотрим влияние указанных факторов на форму эпюр перемещений.

Сравнение рис.7 и рис.8 показывает, что при жёстком основании (вариант №d) осадки экрана распределены по высоте более неравномерно, чем горизонтальные смещения. Это объясняется Sainov, M.P.; Soroka V.В.

Impact of foundation stiffness on the stress-strain state of the concrete face of a rockfill dam;

тем, что периметральный шов обеспечивает возможность смещения нижнего края экрана в сторону нижнего бьефа. При жёстком основании максимальные по величине смещения и осадки наблюдаются примерно на ∇ 45 м.

Уменьшение модуля деформации основания приводит к увеличению смещений (рис.7), осадок (рис.8) и прогибов (рис.9) экрана по всей его высоте, однако более интенсивно перемещения увеличиваются вблизи основания и гребня. Самое большое увеличение всех компонент перемещений происходит вблизи основания. При «мягком» основании максимум смещений экрана наблюдается вблизи подошвы плотины.

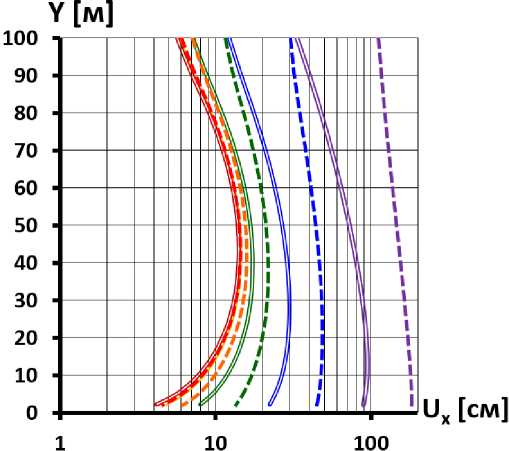
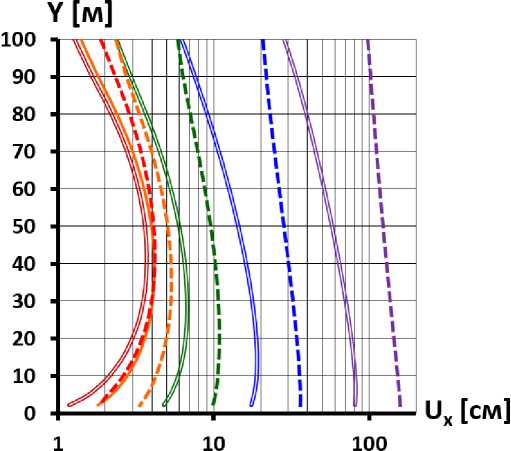
• a) при E к =120 МПа

  b) при E к =480 МПа b) at E k = 480 MPa

  
  

• a)    at E k = 120 MPa

  значения модуля деформации грунта основания E о [MPa]: values of the deformation modulus of the base soil E о [MPa]: — 40   —200   —1000  — 5000  —20000

Рис.7 - Распределение по высоте горизонтальных смещений экрана

Fig.7 - Distribution of horizontal face displacements by height

Пунктирными линиями обозначены перемещения, соответствующие случаю наличия стены в основании, а сплошные линии соответствуют случаю отсутствия стены.

Dashed lines indicate displacements corresponding to the case of the presence of a seepagecontrol wall at the base, and solid lines indicate the case of the absence of a seepage-control wall.

Устройство ПФС влияет на форму эпюры перемещений более сложным образом, по-разному для смещений, осадок и прогибов.

Во всех вариантах устройство ПФС вызывает рост смещений (рис.7). Рост смещений происходит по всей высоте экрана, однако в зоне максимальных прогибов увеличение смещений происходит не так интенсивно, как на гребне и у подошвы.

На форму эпюры осадок устройство ПФС оказывает иное влияние. При устройстве ПФС осадки экрана не увеличиваются, а уменьшаются (рис.8). При этом более интенсивно осадки экрана уменьшаются на гребне плотины (рис.8). Это объясняется тем, что дополнительные горизонтальные смещения вызывают некоторый подъём основания.

Таким образом, устройство ПФС увеличивает смещения экрана, но уменьшает его осадки. Влияние устройства стены на прогибы экрана выражается в некотором росте величин прогибов и в выравнивании их распределения по высоте (рис.9).

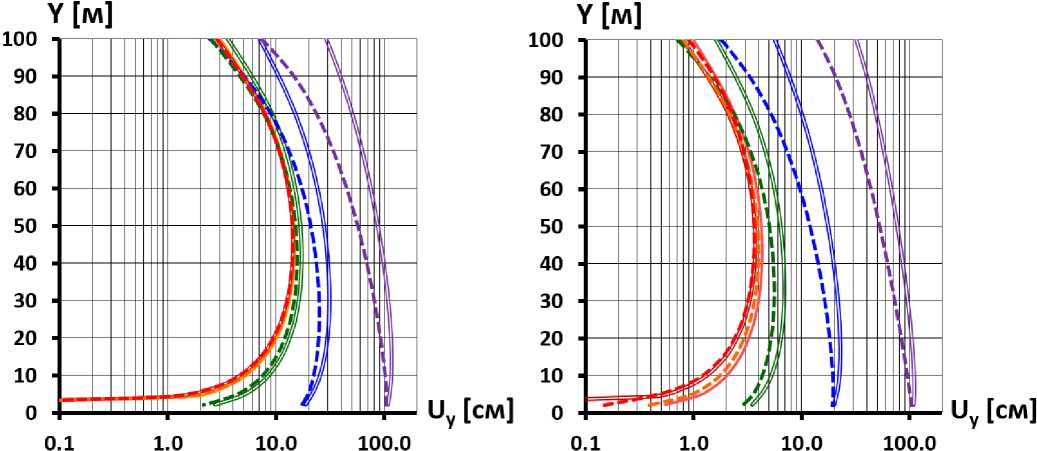
а) при E к =120 МПа

• a)    at E k = 120 MPa

• b)    при E к =480 МПа b) at E k = 480 MPa

значения модуля деформации грунта основания E о [MPa]: values of the deformation modulus of the base soil E о [MPa]: — 40   —200   —1000  —5000  —20000

Рис.8 - Распределение по высоте осадок экрана

Fig.8 - Height distribution of face sediment

Пунктирными линиями обозначены перемещения, соответствующие случаю наличия стены в основании, а сплошные линии соответствуют случаю отсутствия стены.

Dashed lines indicate displacements corresponding to the case of the presence of a seepagecontrol wall at the base, and solid lines indicate the case of the absence of a seepage-control wall.

Оценка количественного влияния рассматриваемых факторов на максимальные величины прогибов U n,max экрана (табл.2) позволила сделать следующие выводы:

• •    При скальном и полускальном основании (E o >1000 МПа) значение U n,max мало зависит от модуля деформации основания E o и в основном определяется модулем деформации каменной наброски E п ;

• •    При нескальном основании (E o <200 МПа) значение U n,max практически не зависит от деформируемости каменной наброски плотины, в основном зависит от модуля деформации основания E o . Эта зависимость – нелинейная. Например, в вариантах серии A (E к =120 МПа) при E o =200 МПа U n,max лишь в 2÷2,5 раза больше, чем при абсолютно жёстком, а при E o =40 МПа – в 7÷10 раз;

• •    При самом «мягком» основании прогибы БЭ (варианты серии «a») составляют более 1% от высоты плотины. По данным натурных измерений на ряде построенных плотин прогибы обычно не превышают 1% от высоты плотины [10];

• •    Влияние устройства ПФС в основании на прогибы экрана существенно слабее, чем влияние деформируемости основания. Чем ниже жёсткость основания, тем влияние ПФС проявляется сильнее. При самом «мягком» основании устройство стены увеличивает прогиб U n,max экрана примерно на четверть.

  
  
  

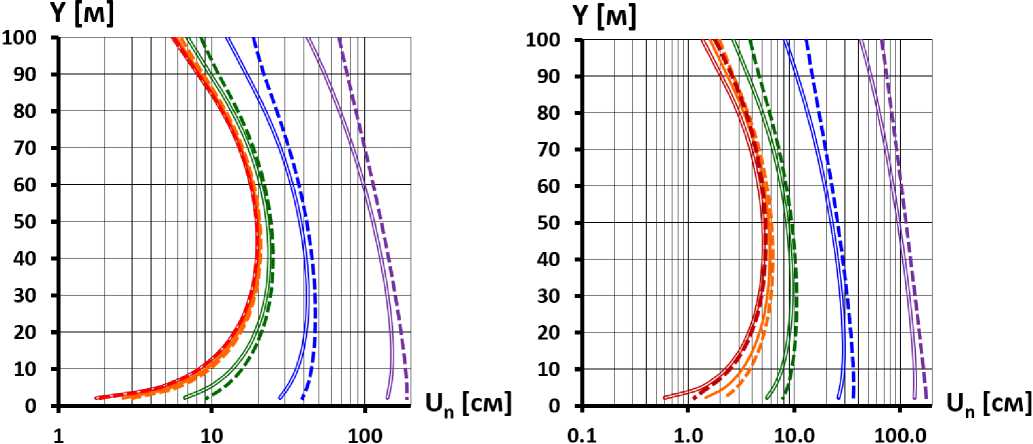
  а) при E к =120 МПа

  • a)    at E k = 120 MPa

  
  

  • б)    при E к =480 МПа b) at E k = 480 MPa

    значения модуля деформации грунта основания E о [MPa]: values of the deformation modulus of the base soil E о [MPa]: — 40    —200   —1000  - 5000  —20000

  
  

Рис.9 - Распределение по высоте прогибов экрана

Fig.9 - Height distribution of face deflections

Пунктирными линиями обозначены перемещения, соответствующие случаю наличия стены в основании, а сплошные линии соответствуют случаю отсутствия стены.

Dashed lines indicate displacements corresponding to the case of the presence of a seepagecontrol wall at the base, and solid lines indicate the case of the absence of a seepage-control wall.

Анализ напряжений в бетонном экране.

Анализ напряжённого состояния бетонного экрана целесообразно проводить по продольным напряжениям σ п , т.е. тем напряжениям, которые действуют в направлении вдоль верхового откоса. Напряжения в направлении поперёк откоса соответствуют гидростатическому давлению и не представляют интереса. Продольные напряжения σ п могут быть растягивающими и сжимающими, поэтому они определяют возможность образования в экране трещин. Распределение продольных напряжений по высоте показано на рис.10-12.

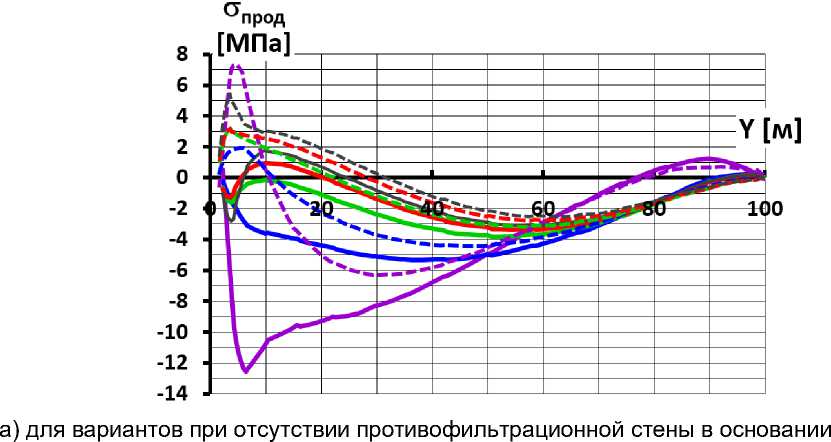
Величины и характер распределения продольных напряжений σ п в экране формируется деформациями поперечного и продольного изгиба, а также деформациями продольного удлинения и укорачивания.

Рис.10 позволяет проанализировать роль в форировании НДС экрана каждого из перечисленнных видов деформаций. На нём показаны напряжения σ п на гранях экрана для вариантов серии A (при E к =120 МПа). Из рис.10 видно, что за счёт изгиба уровень сжатия на низовой грани больше, чем на верховой. Однако изгиб экрана во всех вариантах выражен довольно слабо – разница между значениями напряжений на верховой и низовой гранях, как правило, не превышает 2 МПа. Только в самой нижней части экрана (ниже ∇ 10 м) разница напряжений между гранями (изгибающий момент) резко увеличивается. Она вызвана поперечными и подольный изгибом экрана. Максимальная разница наблюдается в зоне ∇ 3÷4м.

Большую роль изграют продольные деформации экрана (продольное удлинение и укорачивание). Они вызваны трением на контакте экрана с телом плотины и приводят к возникновению в экране продольных сжимающих или растягивающих сил.

a) for variants in the absence of an seepage-control wall in the base

• b)    для вариантов с устройством противофильтрационной стены в основании

• b)    for variants with an seepage-control wall at the base

значения модуля деформации грунта основания E о [MPa]:

values of the deformation modulus of the base soil E о [MPa]: — 40   — 200   — 1000   — 5000   — ОО

Рис.10 - Распределение по высоте продольных напряжений в экране при E к =120 МПа

Fig.10 - Distribution of longitudinal stresses along the height in the face at E k = 120 MPa

Сплошными линиями показаны напряжения на верховой грани, пунктирными линиями – напряжения на низовой грани.

Линии серого цвета соответствуют абсолютно жёсткому основанию.

Все перечисленные эффекты проявляются во всех вариантах, но степень их развития этих деформаций определяется деформируемостью каменной наброски и грунтов основания.

При абсолютно жёстком основании (вариант 1) нижняя часть экрана (ниже ∇ 30 м) испытывает растягивающие продольные силы, а верхняя часть – сжимающие. Изгиб увеличивает растягивающие напряжения на низовой грани нижней части экрана. Самое опасное сечение экрана располагается в самой нижней части экрана (в зоне ∇ 3÷4м). При E к =120 МПа растягивающие напряжения (>5 МПа) намного превышают прочность бетона на растяжение (1,8 МПа) (рис.10а), а при E к =480 МПа прочность обеспечивается.

Рассмотрение вариантов со скальным и полускальным основанием (E о ≥ 1000 МПа) показывает, что уменьшение жёсткости основания (E о ) приводит к уменьшению растягивающих напряжений в экране по сравнению с вариантом абсолютно жёсткого основания (рис.10,а). Чем меньше E о , тем меньше проявляются деформации продольного изгиба и линейные деформации экрана. Длина зоны растягивающих продольных сил с уменьшением E о также уменьшается. Тем не менее, качественная картина напряжённого состояния бетонного экрана не изменяется.

В вариантах с нескальным, «мягким» основанием (E о =40 МПа, 200 МПа) напряжённое состояние бетонного экрана принципиально отличается от напряжённого состояния при жёстком основании. Оно характеризуется наличием в нижней части экрана не растягивающих, а высоких сжимающих сил и напряжений. Например, в варианте 2.A.a (E о =40 МПа, E к =120 МПа) сжимающие напряжения в экране превышают 12 МПа (рис.10,а).

Кроме того, Для нескального основания характерно резкое увеличение изгибающих моментов в нижней части экрана (рис.10), которое во многом нивелирует положительное влияния сжимающих продольных сил. снижение E о приводит к увеличению деформаций продольного изгиба. В варианте 2.A.a (E о =40 МПа, E к =120 МПа) они превышают 7 МПа (рис.10а), а в варианте 2.B.а (E о =40 МПа, E к =480 МПа) – 9 МПа. Такие напряжения много выше прочности бетона на растяжение. Эти напряжения намного превышают растягивающие напряжения при абсолютно жёстком основании.

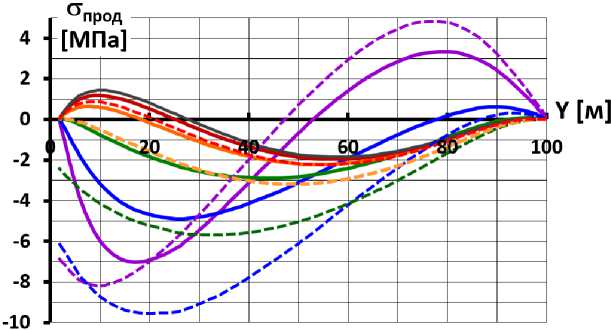
Отдельно следует рассмотреть влияние жёсткости основания на продольные силы. Для этого были построены графики на рис.11, на которых показано распределение средних значений продольных напряжений в экране. На рис.11 хорошо видно, что чем ниже E о , тем выше уровень сжимающих сил в нижней части экрана. Однако при высокой деформируемости основания (E о =40 МПа) в верхней части экрана возникают растягивающие продольные силы. Это связано с тем, что под действием гидростатического давления основание интенсивно расширяется в стороны. В вариантах серии B (E к =480 МПа) этот эффект проявляется ещё сильнее. Можно заключить, что образование растягивающих сил в верхней части экрана характерно для вариантов, в котором основание более деформируемо, чем тело плотины (E о к ).

Таким образом, можно сделать следующие выводы:

• •    Cоотношение деформируемости плотины и основания E к /E о определяет качественную и количественную картину напряжённого состояния экрана. Соотношение E к /E о влияет на характер и величину продольных сил, на величину изгибающих моментов.

• •    Расположение каменно-набросной плотины с бетонным экраном на очень «мягком» основании, создаёт опасность нарушения целостности экрана вследствие потери прочности на растяжение и сжатие.

• •    Для обеспечения надёжной работы экрана соотношение E к /E о не должно превышать 3.

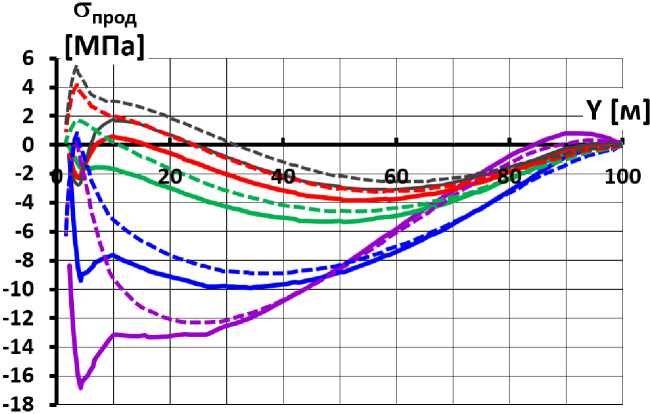
Отдельно рассмотрим влияние на напряжённое состояние бетонного экрана устройства в основании противофильтрационной стены (схема 3). Было выявлено, что вызванные гидростатическим давлением на стену дополнительные смещения усиливают влияние действия жёсткости основания.

Во-первых, в схеме 3 сжимающие продольные силы, которые характерны для нижней части экрана, выше, чем в варианте 2 (рис.11). Приращение сжимающих напряжений тем выше, чем выше деформируемость основания. Увеличение сжимающих напряжений в экране может быть довольно значительным – в некоторых вариантах они увеличиваются на 6 МПа. В варианте 3.A.a (E о =40 МПа, E к =120 МПа) сжимающие напряжения на верховой экране достигают 17 МПа (рис.10,b), что сопоставимо с прочностью бетона на сжатие. Однако увеличение сжимающих продольных сил имеет и положительный эффект – оно «гасит» растягивающие напряжения в экране.

Во-вторых, в схеме 3 увеличиваются растягивающие продольные силы, которые характерны для верхней части экрана при «мягком» основании в варианте 3.В.a (рис.11,b).

Тем не менее, несмотря на большое влияние, изменение схемы действующих нагрузок не меняет качественную картину напряжённого состояния экрана. С этой точки зрения роль жёсткости основания является более значительной, и количественной, и качественной.

a) at the modulus of deformation of the soil of the dam E k = 120 MPa

• a)    при модуле деформации грунта плотины E к =480 МПа

• b)    at the modulus of deformation of the soil of the dam E k = 480 MPa

  значения модуля деформации грунта основания E о [MPa]: values of the deformation modulus of the base soil E о [MPa]: — 40   — 200   — 1000   — 5000   — ОО

Сплошными линиями обозначены варианты, соответствующие отсутствию стены в основании, Пунктирными линиями обозначены варианты, соответствующие наличию стены в основании.

Рис.11 - Распределение по высоте экрана средних значений продольных напряжений для расчётных вариантов деформируемости основания и каменной наброски

• Fig.11 - The distribution of the average values of longitudinal stresses along the face height for the calculated variants of the deformability of the base and rockfill

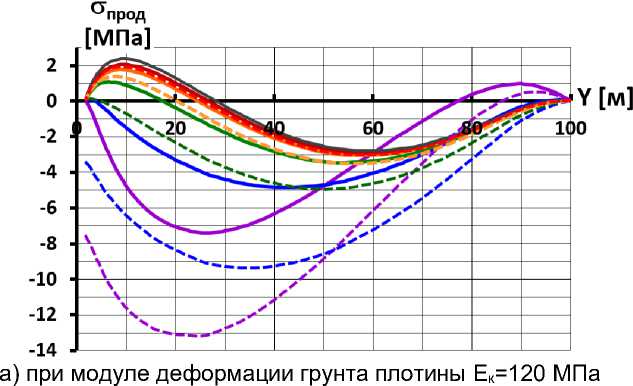
  Даже при самой высокой жёсткости основания напряжённое состояние экрана не соответствует случаю основания бесконечной жёсткости. Рис.12 позволяет сравнить напряжённое состояние экрана для случаев абсолютно жёсткого основания и реального скального основания (с E о =5000 МПа). Хорошо видно, что учёт реальной жёсткости основания учёт показывает более благоприятную картину НДС бетонного экрана. Оно выражается в уменьшении величин и области растягивающих напряжений в экране. Уменьшение расчётных значений максимальных растягивающих напряжений относительно небольшое – от 0,5 до 2 МПа (рис.12 в зависимости от соотношения E о /E к ), но весьма существенно. Можно сделать вывод, что при численном моделировании НДС каменно-набросных плотин с бетонным экраном нельзя принимать основание абсолютно жёстким. Это особенно важно, если тело плотины имеет пониженную деформируемость.

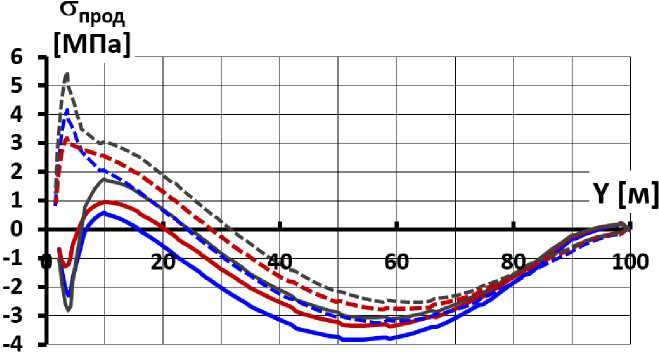
a) при модуле деформации грунта плотины E к =120 МПа

a) at the modulus of deformation of the soil of the dam E k = 120 MPa

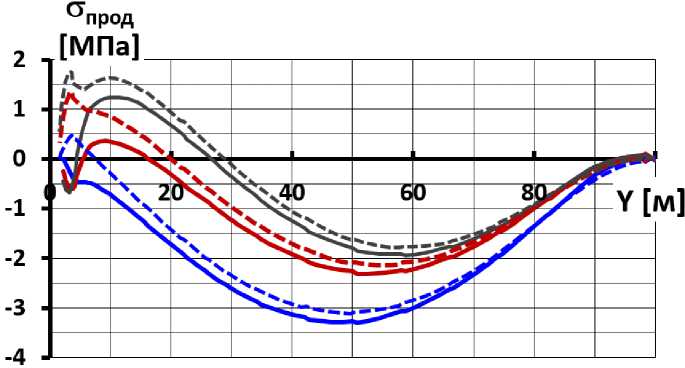
b) при модуле деформации грунта плотины E к =480 МПа

b) at the modulus of deformation of the soil of the dam E k = 480 MPa

Рис.12 - Распределение по высоте продольных напряжений на гранях экрана для различных вариантов устройства основания

Fig.12 - Distribution of longitudinal stresses along the height on the edges of the face for different variants of the foundation device

Серым показан вариант 1 (абсолютно жёсткое основание);

Красным показан вариант 2 (основание конечной жёсткости E о =5000 МПа при отсутствии противофильтрационной стены);

Синим показан вариант 3 (основание конечной жёсткости E о =5000 МПа при наличии противофильтрационной стены);

Сплошные линии соответствуют верховой грани, пунктирные линии соответствуют низовой грани.

Variant 1 is shown in gray (absolutely rigid base);

Variant 2 is shown in red (base of final stiffness E о = 5000 MPa in the absence of an seepagecontrol wall);

Variant 3 is shown in blue (base of final stiffness E о = 5000 MPa in the presence of an seepagecontrol wall);

Solid lines correspond to the top edge, dashed lines correspond to the bottom edge.

4 Conclusions

Полученные результаты позволяют сделать следующие выводы:

• 1.    Жёсткость основания играет очень важную роль в формировании НДС бетонного экрана каменно-набросной плотины. От жёсткости основания зависит характер деформаций тела плотины и, соответственно, внутренние усилия в бетонном экране. При численном Sainov, M.P.; Soroka V.В.

• 2.    Основное влияние жёсткость основания оказывает не на деформации поперечного изгиба, а на продольные силы в экране, вызванные силами контактного трения между экраном и телом плотины. Поэтому количественные оценки этого влияния верны только для рассмотренного значения касательной жёсткости указанного контакта.

• 3.    Даже на очень жёстком, прочном скальном основании напряжённое состояние бетонного экрана заметно благоприятнее, чем при абсолютно жёстком основании. При снижении жёсткости скального основания НДС бетонного экрана качественно не изменяется, но приводит к уменьшению значений растягивающих продольных сил и растягивающий продольных напряжений.

• 4.    Наиболее благоприятное НДС бетонного экрана плотины складывается тогда, когда деформируемость тела плотины примерно соответствует деформируемости основания. В этом случае экран испытывает сжимающие, а не растягивающие продольные силы.

• 5.    НДС бетонного экрана и самой плотины на слабом нескальном основании является неблагоприятным. Это связано с тем, что деформации бокового расширения основания могут вызвать значительные сжимающие и растягивающие продольные силы напряжения. Кроме того, возрастает изгиб нижней части экрана. В этом случае сжимающие и растягивающие продольные напряжения в экране могут быть сопоставимы по величине или превышать прочность бетона. Можно рекомендовать, что соотношение модулей деформации плотины и основания не должно превышать 3. При строительстве плотин на «мягком» основании необходимо снижать деформируемость основания.

• 6.    При «мягком» основании на НДС бетонного экрана оказывает устройство противофильтрационной стены в основании. Гидростатическое давление верхнего бьефа вызывает дополнительные смещения основания, которые увеличивают сжимающие продольные силы в экране.

Impact of foundation stiffness on the stress-strain state of the concrete face of a rockfill dam;

моделировании НДС каменно-набросных плотин с бетонным экраном необходим учёт реальной деформируемости грунтов основания даже тогда, когда основание является скальным. Это связано с высокой степенью уплотнения каменной наброски, благодаря чему её модуль деформации отличается от модуля деформации скалы примерно на один, а не на два порядка. Можно считать, что никакое реальное основание не может считаться абсолютно жёстким.