Влияние жесткости узлового соединения на механические характеристики стеллажа

Разработка и внедрение новых технологий, используемых при возведении зданий и сооружений из металлических конструкций, делает их производство эффективным.

Новое, быстро развивающееся направление в строительстве - применение конструкций, выполненных из легких стальных холодногнутых профилей (ЛСТК). Низкая металлоемкость, рациональные параметры сечения, легкость транспортировки и монтажа конструкций являются основными преимуществами ЛСТК.

Оценка прочностных и эксплуатационных характеристик новых видов сечений, узловых соединений производится в несколько этапов. Первый этап - испытание реальных образцов, второй - расчёт конструкции с применением специализированных программных комплексов. Результаты оцениваются с помощью параметров регламентированных нормативными документами. Эксперименты позволяют определить другие важные факторы, влияющие на эксплуатационные характеристики конструкций, которые изготавливаются по ЛСТК технологии. В частности, определяется долговечность узловых соединений, которые значительно влияют на общий срок службы конструкции.

Актуальными нормативными документами, которые используются при расчете тонкостенных конструкций, являются Еврокод-3 и AJSJ.

Основоположником исследования стержневых тонкостенных конструкций при их деформировании является С.П. Тимошенко [1, 2]. Он разработал методику определения экспериментальным путем жесткости на кручение стержня открытого вида, изучал различные аспекты деформирования тонкостенных стержней различных сечений.

В публикациях В.З. Власова [3–5] представлены принципы расчета тонкостенных конструкций, изготовленных из профилей открытого типа, на прочность и потерю устойчивости при воздействии силы вне "круга устойчивости", на кручение и изгиб. А.А. Уманским [6] было предложено иное решение для задачи на изгиб в условиях стесненного кручения.

Вклад в совершенствование теории расчета ЛСТК внесли Бычков Д.В. в соавторстве с А.К. Мрощинским [7–9]. Они разработали алгоритмы для расчета кручения балок, при учёте количества пролетов и условий закрепления концов. Используя метод сил и перемещений, данный метод расчета позволяет учитывать стесненное кручение тонкостенных конструкций, в частности, рам.

Диссертационное исследование А.Р. Туснина [10] посвящено использованию МКЭ при решении задач деформирования тонкостенных конструкций с учетом влияния изгиба и кручения. Расчет позволяет учитывать влияние разных узловых соединений, а также расположение центра тяжести балки, её прогиба и эксцентриситета.

Работы [11, 12] посвящены усовершенствованию методов расчета тонкостенных конструкций, а также рассмотрены вопросы надежности, долговечности и способы их повышения, отмечена недостаточность нормативной базы, используемой в России, и предложены возможные варианты исправления ситуации.

Примеры реального использования легких стальных тонкостенных конструкций, описание технологий и особенностей монтажа, эксплуатации рассмотрены в [13].

В работе [14] представлен метод расчета тонкостенных конструкций, образованных из элементов составного профиля, который позволяет учитывать влияние формы сечения профиля в условиях общей потери устойчивости по ПНС (предельно-напряженное состояние).

Руководства [15, 16] рассматривают технологии усиления железобетонных конструкций с применением композита (композиционный материал). Исследованы вопросы оценки качества работ, технических требований к применяемым материалам, условий монтажа и эксплуатаций, также представлены примеры усиления конструкций.

Статьи [17–19] посвящены методикам расчета тонкостенных конструкций, которые учитывают деформации и накопления повреждений.

Правила проектирования, формулировки, типовые виды и технические характеристики тонкостенных элементов, основные модели, расчетные схемы и вариации расчета представлены в [20-22].

Авторами [23, 24] сравниваются результаты натурных испытаний типовых профилей с результатами, полученными в ходе моделирования в специализированных программных комплексах.

Вопросы влияния температуры (от низких до высоких, возникающих вследствие пожара) на прочностные и эксплуатационные характеристики тонкостенных конструкций разобраны в [25, 26].

Поведение элементов конструкций из полуоткрытых профилей рассмотрено в [27, 28]. Влияние приложения эксцентриситета нагрузки к элементам из тонкостенных профилей и получение зависимости деформации и прогибов в связи с этим, получены в материалах работ [29,30].

Примеры оценки прочностных характеристик конструкций из материалов разного рода с применением испытаний неразрушающего типа, моделирование конструкций с использованием различных КЭ и сравнение результатов приведены в исследованиях [31–34].

В [35–38] выполнен обзор российских и иностранных источников, в которых уделяется внимание устойчивости тонкостенного элемента холодногнутого изготовления при изгибе. Экспериментальные данные сравниваются с теоретическими показателями, полученными в ходе моделирования с помощью стержневых и оболочечных элементов. Проанализированы результаты, сформулированы проблемы, предложены варианты решения.

Работы [39, 40] посвящены изучению и моделированию расчетной схемы подземного перехода, влиянию расчетной схемы на виды тонкостенных профилей холодногнутого изготовления, которые можно использовать в данном сооружении. Полученная модель позволяет осуществить дальнейшее внедрение тонкостенных холодногнутых профилей при проектировании и строительстве подземных переходов.

Авторы [41–43] представили новую программно-вычислительную систему "Сталькон", разработанную сотрудниками кафедры металлических конструкций МГСУ, которая позволяет производить статический расчет и определять несущую способность тонкостенных стержневых конструкций, в том числе и пространственных систем, учитывая требования нормативной документации. В качестве примера произведен расчет стойки с шарнирно-неподвижным нижним и шарнирно-подвижным верхним концами. Также, проанализирована возможность использования для расчетов ПК NASTRAN и ANSYS, с помощью которых можно рассчитывать тонкостенные конструкции с учетом стесненного кручения.

В работах [44–46] представлена разработка метода численного расчета стержневых тонкостенных конструкций и пространственных систем по полусдвиговой и бессдвиговой теориям. Результаты изучения деформирования открытого тонкостенного стрежня, который работал на кручение с появлением деформации сдвига, опубликованы с учетом применения разных КЭ.

Авторами исследований [47–49] выдвинуты методические обоснования редуцирования, основанные на изменении несущей способности профиля. Проанализированные данные были сопоставлены между собой, и выдвинуто заключение о редуцировании поперечного сечения. В ходе исследований для тонкостенного профиля вычислена эффективная площадь поперечного сечения с учетом возможной местной потери устойчивости. Также проанализированы результаты линейного и нелинейного расчета сжато-изгибаемого стального элемента, выполненного с двойным гофрированием. Полученные результаты сравниваются с результатами натурных экспериментов. Определены особенности работы тонкостенного металлического элемента с двойным гофрированием. Рассмотрены результаты реальных испытаний фермы из тонкостенных профилей холодногнутого изготовления пролетом 18 м.

В работах [50–53] рассмотрены проблемы усталости ЛСТК, предложены возможные методы решения данных проблем, разобраны нелинейные процессы накопления повреждений тонкостенных конструкций и описаны способы прогнозирования усталостной долговечности. Применение энергетической модели оценки прочности элементов при малоцикловой усталости представлено в работах [54–56]. Описан алгоритм кинетического анализа поврежденности и опытным путем доказана адекватность данного метода.

Статьи [57, 58] посвящены оценке влияния механохимического растворения профиля длинных металлических цилиндров на их долговечность под действием собственного или дополнительного веса.

Целью данной работы является оценка жесткости узлового соединения балка-стойка, которое входит в состав тонкостенной пространственной конструкции стеллажа. Для достижения данной цели поставлены следующие задачи:

• •    Создание установки для проведения натурных испытаний с тонкостенными конструкциями;

• •    Построение аналитической конечно-элементной модели конструкций в программном комплексе ANSYS, сравнение полученных результатов с результатами натурных испытаний;

• •    Определение жесткостных характеристик соединения, сравнение натурных и численных результатов.

• 2.    Методы

  • 2.1.    Энергетическая модель оценки прочности

Поврежденностьматериалаконструкцииможетбытьвычисленаспомощьюэнергетической модели накопления повреждений. Энергетический метод определения разрушений заключается в вычислении необратимой работы деформирования A p , которая представлена интегралом истинных напряжений по необратимым деформациям, вызванным этими напряжениями.

A p

■J

Ep

a • ds = C

где е р - деформация разрушения;

• е - истинная необратимая деформация, включающая мгновеннопластические и вязкопластические деформации;

• т - истинное напряжение;

• С - постоянная, зависящая от температуры.

Исходя из предположения, о пропорциональности текущей поврежденности элемента материала по отношению к совершенной на данный момент времени работе, допустимо записать кинетическое уравнение, описывающее меру повреждений П, в виде кинетического уравнения

„ 1 f ,

П = С J т • de.                                                       (2)

Из условия баланса, внутренней энергии элемента материала тела и представленного кинетического уравнения накопления повреждений, поврежденность можно представить в следующем виде:

n = C(A + Q),

где А – текущее значение работы;

Q – текущее значение тепла, приобретаемое в процессе теплообмена.

Значение величины Q является переменным на протяжении различных стадий деформирования, а предельная величина внутренней энергии тела является константой, таким образом получаем, что работа необратимого деформирования также является переменной величиной. Необратимая работа одного цикла нагружения определяется площадью петли гистерезиса (см. рис. 1).

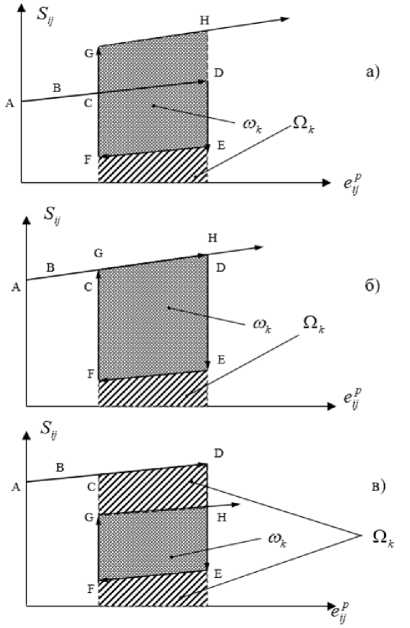
Рис.1. Три характерных типа петель гистерезиса. Показана работа деформирования а) линия циклического нагружения идёт выше линии первоначального нагружения;

б) линии первичного и циклических нагружений совпадают;

в)линия циклического нагружения идёт ниже линии первоначального нагружения. ст и е ^р - напряжение и пластическая деформация.

Полная работа пластической деформации может быть представлена как сумма работ циклической деформации, и одностороннего пластического деформирования.

При нагружении конструкции могут быть реализованы один, два или все три варианта петель гистерезиса.

Для оценки малоцикловой усталости используется соотношение, в котором работа одностороннего и циклического деформирования связаны функциональными зависимостями с поврежденностью элемента.

w w

(N) , V          aW

n(N) =

”+2/U+2/U где amax(N^ - приведенное максимальное напряжение цикла;

а_т - предельное сопротивление материала на разрыв;

^_к - необратимая работа одностороннего пластического деформирования цикла нагружения, представленная площадью под линией EF (рис. 1 а, б) или как разность полной работы и работы циклического деформирования площади петли w_kij (рис. 1 в);

ш_к - необратимая работа циклического деформирования, равная площади петли гистерезиса в к-ом цикле;

• <м _р - предельная работа статического деформирования в опыте на разрыв образца материала.

• 2.2.    Оценка жесткости узлов крепления горизонтальных балок и стяжек к несущим стойкам

В общем случае функции f иф - являются зависимостям, в которых учитываются максимальные напряжения каждого цикла, предельные напряжения и количество циклов до разрушения материала.

Соотношения (1)-(4) модифицированы к такому виду, что могут быть использованы для оценки накопленной поврежденности. Модель накопления повреждений позволяет учесть их накопление при пассивном нагружении.

При оценке критической нагрузки на балочный стеллаж по критерию устойчивости следует учесть крутильную жесткость соединений балка-стойка и стяжка-стойка. Крутильная жесткость соответствует повороту вокруг оси стержня (рис. 4).Предполагалось расчетно-экспериментальное определение только жесткости соединения балка-стойка. Однако, в процессе работы была установлена необходимость учета соединения стяжка-стойка, так как в отличии от паллетных стеллажей, где имеется система косых связей гарантированно удерживающих стеллаж от потери устойчивости с выходом из фронтальной плоскости, в конструкции рассматриваемых вариантов балочных стеллажей предусмотрены лишь горизонтально расположенные стяжки. Поэтому, в таких вариантах стеллажей, возможно проявление формы потери устойчивости с выходом из фронтальной плоскости. Критическая нагрузка, соответствующая этой форме потери устойчивости, в основном определяется жесткостью на кручение узла стяжка-стойка. В работе используется косвенное определение величины жесткости данного соединения не связанное с прямыми измерениями. Для более точной оценки рекомендуется проведение дополнительных исследований.

С целью определения крутильной жесткости узла балка-стойка проведено расчетноэкспериментальное исследование, включающее натурные испытания на упрощенной модели стеллажа, а также расчеты с применением конечно-элементной модели.

Рис. 2 Соединение гребенчатый зацеп (узел балка-стойка, стяжка-стойка)

Испытана и исследована методом конечных элементов модель, пары стяжек длиной 300 мм и пары балок длиной 1500 мм, закрепленных на расстоянии 135 мм от верхнего края стойки. Подпятники не фиксировались специально от перемещения по вертикали и в горизонтальной плоскости, тем не менее в ходе эксперимента не было отмечено никаких перемещений точек опоры стоек. Расстояние между стойками по фронту 1500мм, в перпендикулярном направлении 300 мм.

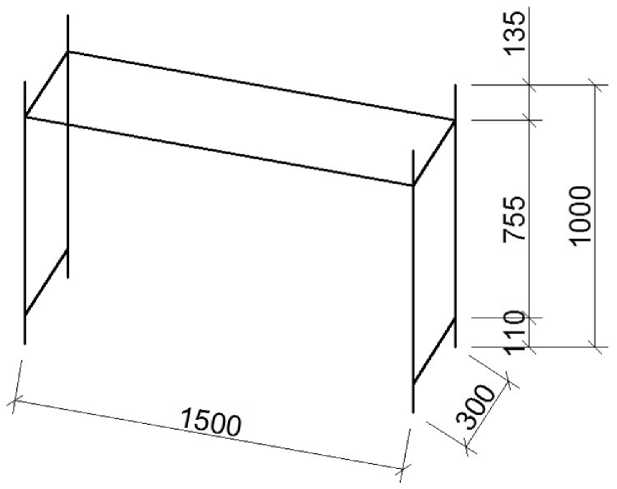
Рис. 3. Геометрические размеры испытываемой модели

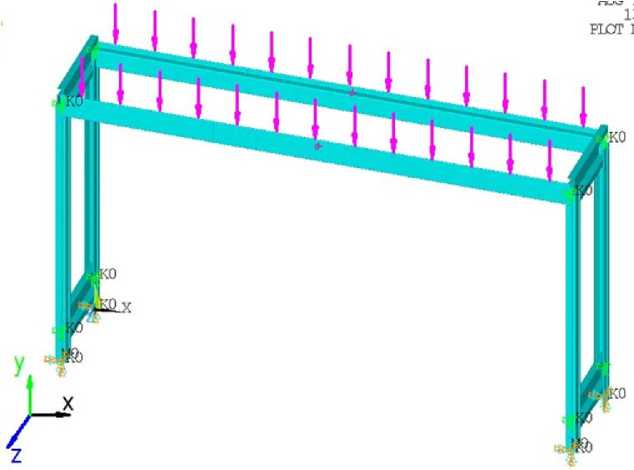
Рис. 4. Расчетная модель для определения жесткости соединения балка-стойка на поворот вокруг оси Z и жесткости соединения стяжка-стойка на поворот вокруг оси X

Балки и стойки конструкции изготовлены из стальной ленты БТ-ПН-1,5, которая соответствует ГОСТ 19904-90. Толщина проката составляет 1,5 мм. Предел текучести применяемой стали равен σ _T = 230 МПа. Сечение несущих горизонтальных балок - закрытого, коробчатого типа. Геометрические характеристики профиля 70х30 мм. Несущие вертикальные балки имеют профиль открытого типа. Размеры - 90х30 мм.

Нагрузка на модель производилась с помощью силовой машины "Armsler" через дополнительную конструкцию, позволяющую имитировать равномерно-распределенную нагрузку. Нагрузка регулировалась с помощью динамометра, закрепленного на подвижной части пресса.

Измерение перемещений исследуемой тонкостенной конструкции производились с помощью нескольких часовых индикаторов. Часовые индикаторы имеют рабочий диапазон от 0 до 80 мм, точность измерения составляет 0,01 мм. Индикаторы определяли перемещения одной из стоек по осям X и Z в её верхней части.

Создан конечно-элементный аналог реальной модели в программном комплексе ANSYS. Моделирование конструкции производилось с помощью балочных конечных элементов, которые позволяют наиболее корректно учитывать форму профиля поперечного сечения балок. Общий вид расчетной модели приведен на рис. 4. Данная модель позволяет определить жесткость узла балка-стойка на поворот вокруг оси Z (деформирование стеллажа в плоскости).

Точки опор стоек связаны с жестким основанием: жестко по перемещениям Ux, Uy, Uz и по повороту Ry; упруго по поворотам Rx, Rz с величинами жесткостей.

Жесткости точки опоры вертикальной стойки (жесткости узла подпятник-стойка) на поворот вокруг осей Xи Z были определены ранее расчетно-экспериментальным путем. В ходе эксперимента подпятники не фиксировались от перемещения по вертикали и горизонтальной плоскости. Точки опор стоек были связаны с жестким основанием: жестко по перемещениям Ux, Uy, Uz и повороту Ry; упруго по поворотам Rx, Rz. Вертикальная стойка крепится к подпятнику 2 винтами-саморезами. Подпятник крепится к полу анкерным болтом. Размер подпятника: высота - 24 мм., ширина - 60 мм., длина - 50 мм.

Рис. 5. Узловое соединение подпятник-стойка

На основе данных экспериментов расчетным путем методом итераций были подобраны значения интересующих крутильных жесткостей, так чтобы первая форма потери устойчивости расчетной модели и отвечающая ей критическая нагрузка совпали с экспериментальными.

Крутильная жесткость узла подпятник-стойка вокруг оси X равна 66 Н^м/рад . Крутильная жесткость узла подпятник-стойка вокруг оси Z равна 134,2 Н^м/рад .

Моделирование передачи нагрузки от балок к стойкам осуществлялось с помощью упругих элементов, работающих на поворот вокруг оси Z.

В эксперименте, в целях безопасности, балки были связаны проволокой так, чтобы не допустить горизонтальный прогиб балок. В расчетной модели это было учтено путем наложения жесткой связи по перемещениям Uz на центральные узлы балок.

Узлы в модели стоек расположены таким образом, что обеспечивается корректный учет эксцентриситета передачи нагрузки от балок к стойкам через гребенчатые зацепы (балки загружают стойку по жесткой стенке).

• 3.    Результаты и обсуждение

• 4.    Заключение

  В ходе работы было исследовано соединение гребенчатый зацеп (балка-стойка), который входит в состав тонкостенной конструкции стеллажа. Результаты, полученные в ходе натурных испытаний с упрощенным вариантом конструкции, сравнивались с данными компьютерного моделирования с применением метода конечных элементов. В результате анализа было установлено, что соединение балка-стойка обладает крутильной жесткостью 2820 Н^м/рад на поворот вокруг оси Z. Входе расчетноэкспериментальных исследований было определено значение критической нагрузки на ярус, при которой в конструкции наблюдается потеря устойчивости. Величина нагрузки составила 11,2 кН.

Результаты эксперимента выглядят следующим образом. Модель при нагрузке 11,2 кН переходит в смежную устойчивую форму равновесия, оставаясь в плоскости без образования заметных пластических деформаций. Это значение нагрузки может быть принято за критическую нагрузку по первой форме потери устойчивости модели.

В соответствии с данными эксперимента расчетным путем методом простых итераций было подобрано значение интересующей крутильной жесткости соединения балка-стойка, так чтобы первая форма потери устойчивости расчетной модели и отвечающая ей критическая нагрузка совпала с экспериментально полученными значениями.

Из результатов расчета следует, что крутильная жесткость соединения балка-стойка для простой модели балочного однопролетного стеллажа вокруг осиZ равна 2820 Н^м/рад . Соответствующая форма потери устойчивости показана на рис. 6. Рекомендуется проведение испытаний для определения зависимости количества ярусов на крутильную жесткость соединения балка-стойка и предельной нагрузки на ярус.

Рис. 6. Первая форма потери устойчивости (деформирование модели во фронтальной плоскости). Критическая нагрузка равна 11,2 кН (эксперимент). Крутильная жесткость соединения балка-стойка вокруг оси Z равна 2820 Н^м/рад

• С целью уточнения полученных данных следует провести:

• •    Расчетно-экспериментальное определение жесткости узлового соединения стяжка-стойка.

• •    Дополнительное исследование жесткости узла балка-стойка при испытании многоуровневой конструкции.

• •    Определение предельных величин нагрузок на ярус многоуровневых стеллажей балочного и комбинированного типа.

• •    Оценку влияния высоты первого нагруженного яруса на величины предельных нагрузок по условию устойчивости на балочные и комбинированные стеллажей различных типоразмеров.

• •    Установление причин неравномерного распределения жесткостей узлов балка-стойка, уровня снижения крутильной жесткости, а также способа учета данного эффекта в расчетах предельных нагрузок на стеллаж балочного типа по условию устойчивости.

• •    Расчетно-экспериментальное исследование поврежденности и живучести конструкции.

• 5.    Благодарности

  Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-08-00845А