Влияния пашенного земледелия на сток взвешенных веществ

В предлагаемой работе используется метод системно-аналитического моделирования (САМ) [1, 2], который был успешно применен для разработки имитационной математической модели водного стока горных рек [3] и стока ВВ [4]. Метод позволяет избежать затратных специализированных исследований, заменяя их архивными данными многолетних наблюдений за динамикой изучаемой характеристики – в нашем случае это концентрация ВВ в водном стоке.

Исходные материалы. С целью выполнения САМ стока ВВ были выбраны 33 речных бассейна Алтае-Саянской горной страны (рис. 1), для которых ранее была разработана модель водного стока [3]. Ограниченное количество ежегодных наблюдений за гидрохимическим стоком Гидрометеорологической службой России определило выбор четырех характерных гидрологических периодов/сезонов: первый (зимняя межень, XII-III месяцы), второй (весенне-летнее половодье, IV-VI), третий (летняя межень, VII-VIII), четвертый (осенняя межень с возможными паводками при сильных дождях, IX-XI). Учитывалось, что в каждом сезоне должно иметься одно или более измерений концентрации ВВ. После их усреднения были получены по четыре среднесезонных концентрации для каждого года наблюдений. В среднем по всем 33 бассейнам концентрации составили 6,48, 13,9 мг/л для 1, 2, 3, 4-го сезонов соответственно, и эти значения были использованы для нормировки всех имеющихся измерений ВВ.

Температуры воздуха и осадки характеризовались нами через доли/проценты от их среднемноголетних месячных значений. Для таких нормированных температур и осадков с помощью разработанного метода обобщения получена единая для всей Алтае-Саянской горной страны их помесячная и межгодовая динамика [5]. Показано, что эта динамика может использоваться в качестве адекватной площадной характеристики изменения метеорологических условий при описании водного стока горных рек [3].

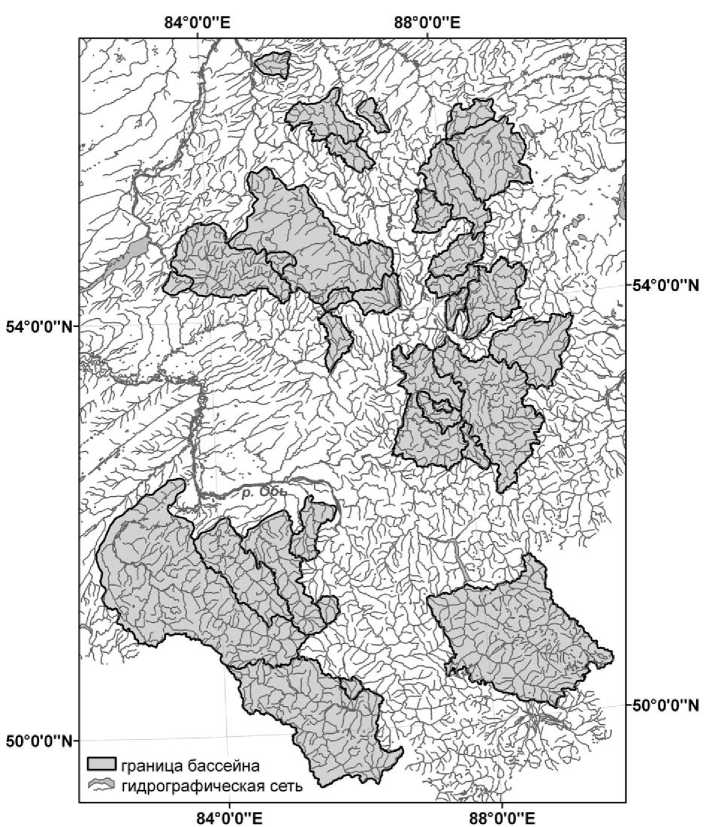
Рис. 1. Карта-схема расположения модельных речных бассейнов Алтае-Саянской горной страны

Для учета ландшафтной структуры речных бассейнов Алтае-Саянской горной страны выделено 12 типологических групп геосистем и отдельно 13-я для аквальных ландшафтов, имеющих незначительную площадь (табл. 1) [6]. Для всех групп в каждом речном бассейне по имитационной модели водного стока горных рек рассчитаны формируемые ими вклады в водный сток [3].

В целом, база данных для разработки модели стока ВВ включала:

• -    1390 среднесезонных нормированных концентраций ВВ в разные годы по 33 речным бассейнам, то есть 1390/4—350 величин для каждого сезона;

• -    расчетный вклад в водный сток от каждой группы геосистем в каждом речном бассейне по каждому году гидрохимических наблюдений (3120, 3480, 3180, 3350 значений водных стоков, нормированных на среднемноголетнее среднесезонное значение стока бассейна, для 1, 2, 3, 4-го гидрологических сезона соответственно);

• -    обобщенные по территории Алтае-Саянской горной страны нормированные месячные осадки и среднемесячные температуры воздуха за период 1951-2003 гг. (по 636 значений);

• -    площадь и средняя высота каждого из 33 речных бассейнов, высота его замыкающего створа, длина речного русла (от истока до створа);

• -    доля площади пашни (при ее наличии) в каждом речном бассейне.

  Таблица 1. Среднесезонные концентрации взвешенных веществ (ВВ) в компонентах водного стока, формируемых ландшафтами Алтае-Саянской горной страны

  Группы геосистем (ландшафтов)	Концентрации ВВ ( a k , b , d в (2)) по 4-м гидрологическим сезонам года (XII-III, IV-VI, VII-VIII, IX-XI мес.), мг/л
  	1	2	3	4
  гляциально-нивальные высокогорья (характеризуются параметром a1 в (2))	1	6	0	0
  гольцово-альпинотипные высокогорья и среднегорья, псевдогольцовые низкогорья ( a 2 )	0	0	0	0
  тундрово-степные и криофитно -степные высокогорья ( a 3 )	20	205	0	0
  лесные высокогорья, среднегорья и низкогорья ( a4 )	4	140	11	7
  экспозиционно-лесостепные и степные высокогорья и среднегорья ( a5 )	24	226	20	0
  лесостепные, степные низкогорья и предгорья ( a 6 )	4	138	22	10
  межгорные котловины с различными вариантами степей и лесостепей ( a7 )	5	0	7	2
  степные и лесостепные подгорные и возвышенные аккумулятивные равнины ( a 8 )	24	50	15	0
  недренируемые слабопроточные интра-зональные и интрапоясные ландшафты ( a 9 )	0	0	0	0
  долины горных рек ( a 10 )	16	114	37	20
  долины равнинных рек ( a 11 )	30	3	29	12
  лесные возвышенные и подгорные равнины ( a12 )	3	0	1	1
  аквальные ландшафты ( a 13 )	16	61	0	0
  подземный сток ( b )	4	–18	4	5
  пашня ( d )	0,06	13,6	1,7	0,9

  
  

САМ стока взвешенных веществ. Основу САМ составляет определение структуры и параметров имитационной модели через решение обратной задачи оптимизационными методами (подробнее см. [1-3]). Путем последовательной проверки различных физически и гидрохимически непротиворечивых зависимостей, описывающих формирование стока ВВ под воздействием факторов среды, определяется система уравнений, дающая наименьшую квадратичную невязку между рассчитанными по модели и наблюдаемыми концентрациями ВВ. Для описания нетривиальных зависимостей процессов от факторов среды в САМ применяется универсальная функция H , задаваемая выражением:

H ( X 1, X 2, Y1, Y 2, Z 1, Z1, X ) =

Y 1 + Z 1 - ( X	- X 1) ,	если	X <  X 1
2 2- Г 1 (X _ X 2 - X 1	X 1 ) + Y 1 ,	если	X 1 <  X <. X 1 ф X 2
Y 2 + Z 2 - ( X	- X 2),	если	X >  X 2
			(1)

X 2, где X1, X2, Y1, Y2, Z1, Z2 – подбираемые параметры; X – какая-либо переменная модели. Функция H является непрерывной кусочно- линейной функцией из трех произвольных линейных фрагментов и позволяет аппроксимировать широкий спектр различных зависимостей между переменными и факторами среды путем изменения значений своих параметров.

Ранее в ходе системного анализа и САМ была разработана имитационная модель стока ВВ для 33 анализируемых речных бассейнов [4]. Уравнения модели учитывали сезонные осадки, средний поперечный уклон и ландшафтную структуру бассейнов. В настоящей работе продолжен системный анализ и САМ воздействующих на сток ВВ факторов среды, включая ранее отсутствующую пашню. Для разработки модели использовались 1390 среднесезонных концентраций ВВ, наблюдаемых в разные годы на замыкающих створах речных бассейнов, а также необходимая картографическая и метеорологическая информация. В рамках САМ было проанализировано воздействие на сток в разные гидрологические сезоны непосредственно пашенного земледелия. В результате получены следующие уравнения среднесезонного стока ВВ:

для первого гидрологического сезона:

Q - C = \ a k - Q k - H ( c i ,c i ,1,1, c 2 , c 3 , P ) - H ( c 4 , c 4 ,1,1, c 5 , c ₆, K) + k

+ b -ql+ d - Si - Q

(2а)

для второго, третьего и четвертого гидрологических сезонов:

Q • C = ^ a k • Q k • H ( c 1 ,c _p1,1, c 2 , c 3 , P ) • H ( c 4 , c 4 ,1,1, c ₅, c ₆, K ) + k

+ b • q1+d • VSi • Q‘

(2б)

где Q • C - среднесезонный сток ВВ; Q‘ -расчетный среднесезонный водный сток для замыкающего створа бассейна с номером i =1-33 в текущем году [3]; C i - наблюдаемые концентрации ВВ в речном стоке; P - обобщенные по территории Алтае-Саянской горной страны нормированные осадки [5] за IX-XI месяцы предшествующего года для 1-го сезона или за IV-VI, VII-VIII, IX-XI месяцы для 2, 3, 4-го сезонов соответственно; a k - параметры, отвечающие постоянной среднесезонной концентрации ВВ в расчетном среднесезонном водном стоке Q_k ⁱ , формируемом k-о й группой геосистем за счет осадков P , к 1-13; b - параметр, сопоставляемый с постоянной среднесезонной концентрацией ВВ в расчетном приходящем (или уходящем) среднесезонном подземном водном стоке q * , который формируется в бассейне i почвенногрунтовыми водами и водами зон трещиноватых пород; K - средний поперечный уклон бассейна i , рассчитываемый по картографическим данным [4]; H - кусочно-линейная функция (1); c 1^6 - параметры, отражающие влияние на сток ВВ осадков P и уклона K i ; d - параметр, характеризующий увеличение концентрации ВВ в Q ⁱ от каждого процента площади S i ; S‘ - относительная площадь пахотных земель (в процентах от площади бассейна i ). Вместе с подмоделью пространственного обобщения и нормировки среднемесячных температур и месячных осадков [5], подмоделью водного стока [3] уравнения (2а), (2б) составляют полную имитационную модель стока ВВ.

В правой части уравнений (2) суммируются вклады в сезонный сток ВВ от каждой группы геосистем, обеспечиваемые поверхностным, внутрипочвенным и подземным водными стоками. Также отражена роль пашни. На вклад к-ой группы геосистем влияют осадки P за рассматриваемый гидрологический сезон и поперечный уклон Ki речного бассейна. Вклад b • q1 в (2) через отрицательное или положительное значение концентрации ВВ в подземных водах (табл. 1) может учитывать эффект осаждения или, наоборот, повторного взвешивания ВВ из донных отложений. Рассчитываемое по модели водного стока [3] значение q* включает вклад осадков предыдущего сезона и обмен влагой с почвенно-грунтовыми водами и водами зон трещиноватых пород.

В ходе САМ путем решения обратной задачи для каждого из четырех рассматривемых гидрологических сезонов были найдены все параметры a , b , c , d в уравнениях (2) (табл. 1). При этом значения параметров а_к , где к =1-13, характеризуют постоянные среднесезонные концентрации ВВ в водных стоках от каждой из 13 групп геосистем Алтае-Саянской горной страны.

На рис. 2 приведены полученные зависимости среднесезонного стока ВВ от двух входных факторов модели: среднего уклона поверхности K и обобщенных нормированных осадков. В качестве образца ландшафтной структуры использован бассейн верховья р. Катунь с замыкающим створом около с. Тюнгур. На рисунке демонстрируется как изменялся бы сток ВВ при разных уклонах и осадках, если ландшафтная структура бассейна остается неизменной. Обсуждение характера зависимостей можно найти в [4].

Обсуждение результатов моделирования. Согласно уравнениям (2) влияние распашки почв на сток ВВ зависит от времени года. Для первого гидрологического сезона (зимняя межень, XII-III месяцы) в (2а) получена прямо пропорциональная зависимость соответствующей части стока от площади пахотных земель. Очевидно, это обусловлено проникновением почвенных частиц в почвенно-грунтовые воды по всей площади пашни и формированием этими водами стока ВВ в зимнюю межень, когда отсутствуют поверхностный и внутрипочвен-ный водные стоки. Для остальных сезонов в (2б) формируемая пашней часть стока ВВ оказалась пропорциональной квадратному корню от площади пахотных земель, то есть их линейному масштабу. Такая зависимость объясняется наличием в эти сезоны поверхностного и внут-рипочвенного склоновых стоков воды, смывающих почвенные частицы в речной водоток по сути лишь с нижней границы пашни.

Для оценки степени адекватности (2) воспользуемся предложенным ранее универсальным критерием [3-5]:

A = S  /V2 S разн         набл

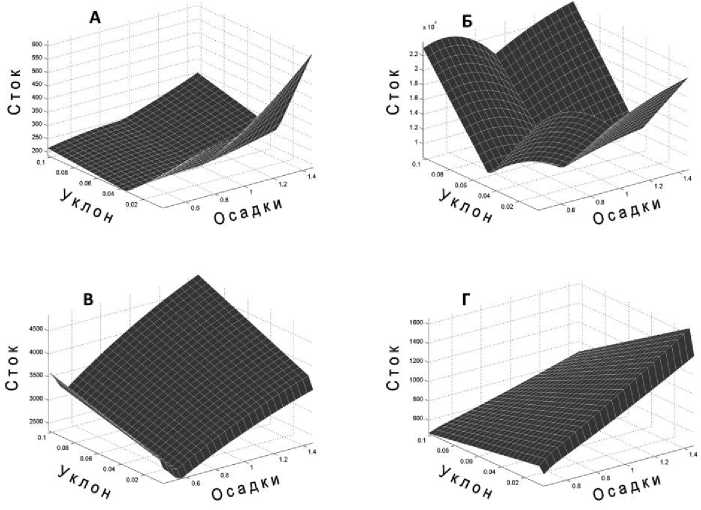
Рис. 2. Зависимость стока ВВ (гр/сек) от среднего уклона речных бассейнов и нормированных осадков для Алтае-Саянской горной страны:

А - 1 гидрологический период/сезон (зимняя межень, XII-III месяцы), осадки за IX-XI месяцы предшествующего года; Б - 2 сезон (весенне-летнее половодье, IV-VI), осадки за IV-VI месяцы текущего года; В - 3 сезон (летняя межень, VII-VIII), осадки за VII-VIII; Г - 4 сезон (осенняя межень, IX-XI), осадки за IX-XI.

где A - критерий адекватности; S разн - стандартное (среднеквадратичное) отклонение для разности сравниваемых расчетного и наблюдаемого рядов моделируемой характеристики, S_Ha6 , - стандартное отклонение для наблюдаемого ряда, 1/V2 =0,71- множитель.

Критерий A в (3) отличается от часто используемого показателя RSR [7, 8] множителем 0,71. Согласно правилам сложения дисперсий расчетного и наблюдаемого рядов мы имеем следующие характерные значения A :

• -    от 0 до 0,71 - различная степень идентичности рядов и адекватности модели с наилучшей при 0;

• -    от 0,71 до 1 - модель имеет низкую адекватность и плохо отражает закономерности, присущие наблюдаемому ряду. Для прогностических оценок вместо нее лучше использовать среднее значение характеристики;

• -    более 1 - дисперсия расчетного ряда больше, чем у наблюдаемого. Иногда необходимо сохранение какой-либо моделью/подмоделью дисперсии наблюдаемого ряда при ее использовании в расчетах в других моделях/подмоделях. В таких случаях модель лучше заменить на случайные вариации характеристики около среднего значения с дисперсией, отвечающей наблюдаемому ряду. В этом случае критерий A будет равен 1. Вернемся к имитационной модели стока ВВ, включающей пространственное обобщение и нормировку среднемесячных температур и

• месячных осадков [5], расчет водного стока [3] и уравнения (2) как три связанные подмодели.

Критерий адекватности A для обобщенных нормированных температур и осадков составляет 0,39 и 0,62 соответственно, а для расчета водного стока в среднем по четырем выделенным гидрологическим сезонам - порядка 0,6. Для оцени адекватности уравнений (2) воспользуемся расчетным и наблюдаемым рядами концентрации ВВ в речном стоке. Критерий A по отдельным гидрологическим сезонам оказался равным: 1 сезон - А=0,61; 2 сезон - А=0,59; 3 сезон - А=0,64; 4 сезон - А=0,67. По правилу сложения дисперсий погрешность расчета стока ВВ должна быть заметно больше каждой из погрешностей расчета осадков и водного стока. Мы же видим, что критерий A мало изменился по сравнению с его значениями для этих переменных модели. Отсюда можно сделать вывод, что уравнения (2) с высокой степенью адекватности описывают интегральные гидрохимические процессы в речных бассейнах и дают малый собственный вклад в общую погрешность расчетов стока ВВ.

По разработанной модели стока ВВ можно рассчитать среднемноголетние концентрации ВВ по гидрологическим сезонам, а также их сезонную и межгодовую динамику для любой точки любой реки Алтае-Саянской горной страны, причем при отсутствии каких-либо гидрохимических наблюдений. Для этого используется единая для всей Алтае-Саянской горной страны по-месячная многолетняя динамика нормированных месячных температур и осадков [5]. Такая дина-мика и соответствующая картографическая информация о водосборной территории, отвечающей выбранной точке реки, позволяют найти по модели водного стока [3] все входящие в (2) доли стока от каждой группы геосистем ( Qi / Qi) и подземного стока ( qi / Qi ). Путем их подстановки вместе с параметрами модели (табл. 1) в уравнения (2) находятся все искомые концентрации ВВ. При наличии наблюдений по водному стоку за 1-2 года, позволяющих восстановить динамику его ненормированных значений [3], с помощью разработанной модели аналогичным образом рассчитывается межсезонная и межгодовая динамика непосредственно стока ВВ.

Выводы:

• 1.    С помощью САМ разработана универсальная модель стока ВВ для расчета его сезонной и многолетней динамики в речных бассейнах Ал-тае-Саянской горной страны. Модель характеризует основные особенности гидрологических и гидрохимических процессов в разные гидрологические периоды года и применима для произвольных бассейнов исследованной территории даже в отсутствие соответствующих гидрохимических наблюдений.

• 2.    Показано, что сток ВВ в реках Алтая зависит как от ландшафтной и орографической структур водосборной территории, метеорологических факторов, так и наличия в речных бассейнах пашни. Установлены зависимости стока ВВ от площади пашни в разные периоды года: если в зимнюю межень добавка к стоку ВВ пропорциональна этой площади, то в остальное время года она пропорциональна квадратному корню из нее, то есть линейному масштабу пахотных угодий.

Работа выполнена в рамках Государственного задания по проекту VIII.76.1.4.