VLSI Circuit Configuration Using Satisfiability Logic in Hopfield Network

Published Online September 2016 in MECS

• I.    Introduction

  Very Large Scale Integration (VLSI) is a process of creating a circuit with thousands of transistors in a single chip. VLSI had been implemented in numerous application in electronic circuit (EC) such as CPU, RAM and ROM. The concept of VLSI helps the integrated circuit designer to combine thousands of transistors in a single chip. Structured VLSI design were coined by Carver Mead and Lynn Conway in 1980. VLSI structure consists of repetitive arrangement of rectangular macro blocks which are connected by background wire [30]. This blocks consist of discrete bits and each bit will contribute to VLSI function. According to Moore’s law, the number of transistor per chip will be double in each

technology generation [31]. The complexity of the VLSI design will increase as the number of electronic components increase. This design lead to rapid development of optimal VLSI design. Moreover, the discrete nature of VLSI design makes it became popular in the combinatorial field.

Traditionally, late error detection in the VLSI design phase is a major cause of unexpected delays in the real circuit hardware [6, 12]. This problem inspires researchers to create model verification techniques which help in earlier error detections. For many practical reasons, it is becoming increasing difficult to manually build a functional VLSI circuit. Modern VLSI usually integrated with static complementary logic gate structures [13, 16]. Logic gate design in VLSI structure is a methodology that drives an output to either high or low. Neural network hold considerable promise in rapid model creation of VLSI design [4, 11]. By assuming binary input as signals, Boolean logic can be used to represent logic construct in VLSI design. Asynchronous circuits are fundamental in many high performance digital computer systems [6, 12]. Due to its importance in vast applications, the features of asynchronous circuits cannot be ignored. Asynchronous design is proven to be extremely complex and most cases can be formulated as satisfiability problem [10, 14]. Method to solve satisfiability problem play an important role in computing theory and system.

Recurrent neural network are essentially dynamical systems that feedback signals to themselves. Popularized by John Hopfield, these models possess a dynamical system with stable states with each own basin and attraction [17]. Hopfield neural network minimizes Lyapunov energy due to physical spin of the neuron states. Content addressable memory feature in Hopfield network is proven to be very useful to solve combinatorial optimization problem [3, 24]. The network produced optimal output by minimizing the network energy. Gadi Pinkas and Wan Abdullah [2, 5] defined a bi-directional mapping between logic and energy function of symmetric neural network. To frame their novelty, both method are applicable to validate the solution obtained are models for a corresponding logic program. The work of Sathasivam [2] showed that the optimized recurrent Hopfield network could be possibly used to do logic programming. Intelligent way of defining connection strength of the logic helps the network to suppress spurious state [1, 5]. In this paper, we proposed Hopfield network to model circuitSAT. The main idea of these simulations is to demonstrate the computational power of collective HNN-kSAT in modelling optimized VLSI circuit.

This paper has been organized as follows. In section II, the fundamental theory of satisfiability problems, namely 2-Satisfiability (2-SAT) and 3-Satisfiability are discussed. Section III emphasizes the concept of VLSI circuit satisfiability, including the fundamental concept of Boolean circuit and the VLSI reconstruction. Furthermore, section IV revolves around the Hopfield neural network and logic programming. Meanwhile, in section V, theory implementation of the networks are been discussed. Finally, section VI and VII enclose the experimental results and conclusion.

• II.    Satisfiability (SAT) Problem

Satisfiability (SAT) is an elementary problem in computer science and mathematics [22]. In VLSI circuits, the transistor problem works similar way as the satisfiability problem. Hence, in order to check the functionality of the VLSI circuit, we opted to integrate the satisfiability problem.

Strictly speaking, a Boolean formula is satisfiable if there exists an assignment of values true and false that renders the entire expression true [27, 29]. The most popular method is exhaustive search, where SAT will try out every possible truth assignment. For instance, given a problem size n , there will be 2 ⁿ such assignments and l literals to set for each assignment [1, 20]. Hence, this method involves O ( l .2 n ) operations [24]. Hence in general, SAT is an NP-complete problem.

The satisfiability problem concerns Boolean variables or expressions in conjunctive normal form (CNF). CNF comprises of conjunction of clauses, where a clauses are disjunction of literal [3]. Literal is a variable or its negation. For instance:

( x 1 v x ₂ ) л ( — x ₂ v x 3 v— x ₅ ) л ( — x 1 v x ₄ ) (1)

Here x ₁, x ₂, x ₃, x ₄are Boolean variables to be assigned, — means negations (logical NOT), v means negations (logical OR), л means negations (logical AND). According to formula in 1, it will be satisfied when x 1 = true , x ₂ = false , x 3 = false , x 4 = true it takes on the value of true. However, if a formula is not satisfiable, it is termed unsatisfiable, that means that it takes on the value false on any value of its variable.

In VLSI problem, we integrate the core concept of satisfiability in order to obtain correct circuit. The literals in every clauses will be represented by using the transistor. Hence, the ability for the transistor to generate 5V is vital in the circuit functionality.

• A.    2-SAT

2-SAT can be defined as a conundrum of determining satisfiability of sets of clauses with at most two literals per clause (2-CNF formulas) [29]. Besides, it is an exceptional case of general Boolean satisfiability which can involve constraints on two variables [19, 22]. In addition, the variables can allow two possibilities for the value of each variable. 2-SAT problem can be expressed as 2-CNF (2-Conjunctive Normal Form). Randomized 2-SAT problem is considered as NP problem or non-deterministic problem [28]. The three fundamental components of 2-SAT are summarized as follows:

• 1.    A set of m variables, x ₁, x ₂,......, x_m

• 2.    A set of literals. A literal is a variable or a negation of a variable.

• 3.    A set of n distinct clauses: C ₁, C ₂........ C_n . Each

clause consists of only literals combined by just logical OR ( ^v ). Each clause must consist of 2 variables.

The Boolean values are { 1, - 1 } . Researchers have replaced F and T in the neural networks by 1 and -1, respectively to emphasized false and true [13, 29]. Since each variable can take only two values, a statement with n variables requires a table with 2 ⁿ rows. The goal of the 2-SAT problem is to determine whether there exits an assignment of truth values to variables that makes the following Boolean formula P satisfiable.

n

P =л C i                  (2)

i = 1

Where л is a logical AND connector. C i is a clausal form of DNF with 2 variables. Each clause in 2SAT has the following form

n

C i = v ( x , y i )                   (3)

x i e { k i , — k i } and y i e { r i , — r i } — k i and — r i are negations of the literals.

• B.    3-SAT

In this paper, we emphasize a paradigmatic NP-complete problem namely 3-Satsifiability (3-SAT). Generally speaking, 3-SAT can be defined as a formula in conjunctive normal form where each clause is limited to at most or strictly three literals [22, 26]. The problem is an example of non-deterministic problem [28]. In our analysis, the following 3-SAT logic program which consists of 3 clauses and 3 literals will be used. For instance:

P = ( A v B v C ) a ( A v B v C ) a ( A v B v D ) (4)

We represent the above 3 CNF formula with P. Thus, the formula can be in any combination as the number of atoms can be varied except for the literals that are strictly equal to 3. Hence, it is vital for combinatorial optimization problem. The higher number of literal in each clause will increase the possibilities or chances for a clause to be satisfied [29].

The general formula of 3-SAT for conjunctive normal form (CNF):

n

A i = 1 Zi

So, the value of k denotes the number of satisfiability [19]. In our case, k-SAT is 3-SAT.

k

Zi = A j = 1⁽ x j , У ч , z ч ), k >  ^{3              (6)}

• III.    VLSI Circuit Satisfiability

  VLSI circuit satisfiability is a brand new research area, producing a prolific amount of research. The VLSI circuit design is inspired by the Boolean circuit concept and the other optimization algorithms. Sethuram & Parashar (2008) has developed the Ant Colony Optimization approach to represent the digital VLSI circuits [32]. On the other hand, some researchers had ventured to model the VLSI circuit by using conventional approach, which is by converting the circuit information into Conjunctive Normal Form (CNF) instances. However, the method results in the loss of the circuit structural configuration especially if the number of the circuit components is getting higher. As a result, we proposed a VLSI circuit based on Boolean circuit by taking into consideration the 3-SAT instances. The integration of 3-SAT instances are able to solve large SAT problems with more of clauses and variables (transistors) by utilizing any advanced intelligence network. Hence, we developed a hybrid model by using Hopfield neural network, logic programming and 3-SAT to configure the input transistor in the VLSI circuit.

• A.    Boolean Circuit

A Boolean circuit is a mathematical model for actual logic circuit. Boolean circuit are defined in terms of logic gates which define them. The establishment of the Boolean circuit can be represent in binary input which contain operator such as AND, OR and NOT gates [10, 12]. Each gate corresponds to Boolean function that takes an input bit string and translates it into output bit string [7, 11].

Given a finite set V of Boolean variables, S over V is a set of equation of the form V = f ( v 1 , v 2 V k ) where v 1 , v ₂, v k e V and f is an arbitrary Boolean function.

The variables of S corresponds to the gates of the circuit. A variable can be in the form of “True” or “False”.

A truth valuation of S is a function Г : V ^ { True , False } .Valuation is consistent if Г ( V ) = f ( Г ( v 1 ) , Г ( v ₂ ) Г ( v k ) ) hold for each equation V = f ( v 1 , v 2 , v_k ) in S .A system S is functional if there exist a consistent valuation for it. The question of whether a system is satisfiable or not, can be considered as NP-complete problem [14]. Note that Boolean Circuit has exactly 2 ⁿ consistent truth assignments, where n is the number of input gates in the circuit [9, 13].

Therefore in case of modelling Boolean circuit, we are interested in the constrained satisfaction problem [11]. Given that the variable in C ⁺ с V must be true and those C - с V false which is the constraint of the circuit. Figure 1 shows how logic gate in Boolean circuit can be visualize in Quad 2 component.

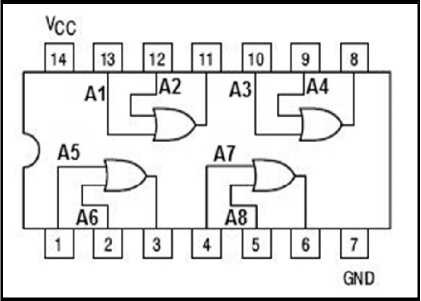
Fig.1. Schematic Diagram of SN74LS32N Quad 2-Input OR Gate

Finding a correct design model circuit is NP problem. The output of the circuit can be physically determined by using any electronics device such as light bulb or ammeter. If the output of the circuit is 1 the bulb will light up or ammeter will show deflection.

• B.    VLSI Reconstruction

In essence, Very Large Scale Integration (VLSI) is a process of combining thousands of transistors into a single chip [33]. Transistor is a semiconductor device used to amplify or act as an automatic switch in integrated circuits [6, 9]. It is composed of semiconductor material with at least three terminals for connection to an external circuit [17, 35]. Transistor consists of base, collector and emitter. In this case, we only consider npn transistor since npn transistor always give us forward bias current. Figure 3 shows a simple diagram of npn transistor.

Modelling a correct VLSI circuit can be treated as combinatorial problem [16]. We are required to find a functional VLSI design model. Figure 2 shows an example of a single unit of a transistor in integrated circuit.

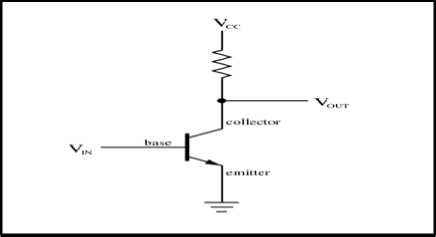
Fig.2. npn-Transistor

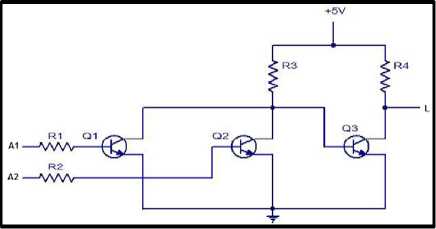
Fig.3. The Input Transistor OR gate

Based on the figure 3, when the inputs A1=0V and A2 = 0V both the transistors Q1 and Q2 are at OFF state (-1). At the same time, transistor Q3 received enough base drive from the supply +5V through resistor R3. Transistor Q3 will be turned ON. The output of the system is given L = V_ee corresponds to 0V (-1). When either the inputs A1 and A2 or both the inputs are equal to +5V (1), then the corresponding transistors either Q1 or Q2 will be ON (1) or both the transistors Q1 and Q2 will be ON (1). The voltage at the collector of transistor Q1 is L = V _ce which corresponds to 0V (-1). During this phase, transistor Q3 doesn’t forward bias and the base-emitter junction and turns OFF (-1) (No voltage drop across it). Hence the final output voltage corresponds to +5V (logic state 1).

• IV.Neuro-LogicinHopfieldNeuralNetwork

Neuro-logic is the combination of neural network and logic programming as a single hybrid network. Basically, the neuro-logic approaches can be applied in a vast fields such as combinatorial optimization, pattern recognition and circuit reconstruction. In this paper, we implement the Hopfield neural network and logic programming to configure the information needed for a VLSI circuit based on 3-SAT instances. The core impetus of this neuro-logic paradigm is to configure the VLSI circuit in a better way. It can be a robust technique in detecting the early fault in the VLSI circuit. Thus, it will assist us in designing a VLSI circuit with higher complexity. Thus, we can implement the proposed technique in the construction of VLSI circuits for sophisticated electrical device. The effectiveness of neuro-logic paradigm in configuring the VLSI circuit will be discussed in Section VI.

• A.    Hopfield Model

In VLSI reconfiguration, we choose the Hopfield neural network because it is distributed and easy to implement. The ability for the transistor in VLSI model to function properly is vital in getting the correct circuit. In our study, we integrate the 2-SAT and 3-SAT problem with Hopfield network in order to relate it with our VLSI reconfiguration conundrum. The correct circuit will be based on the functionality of the transistor. Generally speaking, the Hopfield neural network is an ordinary model for content addressable memory (CAM) [24]. This features imitates our biological brain whereby learning and retrieving data are the building block of content addressable memory (CAM) [2, 3]. In our case, the VLSI model will be having the possible satisfied transistor combination in order to get the correct circuit.

Strictly speaking, Hopfield neural network is a class of recurrent auto-associative network [17, 34]. The units in Hopfield models are principally binary threshold unit [27]. Hence, the Hopfield nets will take a binary value such as 1 and -1. The definition for unit I’s activation, a _i are given as follows:

[ 1 if £ W j S j > ^ « , =] j (7)

[- 1 Otherwise

Where W_ij is the connection strength from unit j to i . S j is the state of unit j and ^ i is the threshold of unit i . The connection in Hopfield net typically has no connection with itself W ii = 0 and connections are symmetric or bidirectional [4, 24].

Hopfield network work asynchronously with each neuron updating their state deterministically. The system consists of N formal neurons, each is described by an Ising variable. Neurons are bipolar Si e {1,-1} obeying the dynamics Si ^ sgn( hi) where the local field hi .The connection model can be generalized to include higher order connection. This modifies the field to hi=zLW/2) Sj+ J^ (8)

The weight in Hopfield network is constantly symmetrical. The weight in Hopfield network refers to the connection strength between the neurons. The updating rule maintains as follows:

S i ( t + 1 ) = sgn [ h ( t ) ] (9)

This properties guarantee the energy will decrease monotonically even though following the activation system [23]. Hence, it will drive the network to hunt for the minimum energy. The following equation represents energy for Hopfield network.

E = .... - 2 XX W²⁾SS j - X W-¹¹ S j      (10)

iji

• B.    Logic Programming in Hopfield Network

Fundamentally, logic programming can be treated as a problem in combinatorial optimization standpoint [22]. Therefore, it can be carried out in a neural network to obtain desired solutions. Logic programming is user writable and readable [29].

Implementation of HNN-2SAT and HNN-3SAT in Logic Programming.

• i.    The 2-SAT and 3-SAT clauses are translated and transformed into Boolean algebra. Basically, the clauses will form a formula that will determine the overall satisfiability. In VLSI circuits, the clauses are referring to the transistor combination in order to generate 5V output.

• ii.    Identify a neuron to each ground neuron.

• iii.    Initialize all connection strengths or weights to zero.

• iv.    Derive a cost function that is related with negation of all 2-SAT and 3-SAT clauses. For instance, X = 2 ( 1 + S x ) and X = 2 ( 1 - S x ) . S x = 1 (True)

and S x = — 1 (False). Multiplication represents conjunction and addition represents disjunction.

• v.    Comparing the cost function with energy, E by obtaining the values of the connection strengths. (Sathasivam’s Method) [2, 24]

• vi.    Check clauses satisfaction by using exhaustive search. Hence, the satisfied clauses will be stored. In VLSI circuits, the satisfied assignments for transistors will be stored as content addressable memory (CAM).

• vii.    The states of the neurons are randomized. The network undergo sequences of network relaxation [24]. Compute the corresponding local field h i ( t ) of the state. If the final state is stable for 5 runs, we ponder it as final state.

viii. Find the corresponding final energy E of the final state by using Lypunov equation. Validate whether the final energy obtained is a global minimum energy or local minima. In VLSI circuit, the final energy depicts the correct configuration of the circuit. Next, the circuit accuracy and runtime are computed for every VLSI models.

• V.    Implementation

For implementation, firstly, we generate random program k-SAT clauses. From there, we initialized initial states for the neurons in the clauses. The network will evolve until final state reached. Once the program has reached the final state, the neuron state is updated via equation (9). As soon as the network relaxed to an equilibrium state, test the final state obtained for the relaxed neuron whether it is a stable state. Stable state will be considered provided the state remains unchanged for five runs. According to Pinkas [18], letting an ANN to evolve eventually shall lead to stable state where the energy function obtained does not change further. In this case, the corresponding final energy for the stable state will be calculated. If the difference between the final energy and the global minimum energy is within the given tolerance value, then consider the solution as global solution.

• VI.    Results and Discussion

The performances of our proposed paradigm have been evaluated based on global VLSI configuration, circuit accuracy and the runtime.

• A.    Global VLSI configuration

Table 1. Global VLSI configuration for HNN-2SAT circuit

Number of Transistors	The Correct VLSI Models
20	9976
40	9825
60	9756
80	9787
100	9524
120	9132

Table 2. Global VLSI configuration for HNN-3SAT circuit

Number of Transistors	The Correct VLSI Models
20	9980
40	9901
60	9826
80	9698
100	9586
120	9233

Table 1 and 2 elucidate the global VLSI configuration for different number of transistors. The result of the transistor HNN-2SAT and HNN-3SAT problem are summarised in table 1 and table 2 respectively. In this study, we are successfully reconstruct the VLSI models via computer simulations. The ability for the proposed algorithm can be analysed by looking at the number of correct VLSI models for higher number of transistors. The proposed algorithm had retrieved the correct transistor model for the circuit. It can be deduced that, almost 90% of the HNN-2SAT and HNN-3SAT model having 5V output. As the number of transistor increased, the retrieval power of HNN-2SAT and HNN-3SAT decreased. This is due to spurious effect of the network that cause the network to stuck at sub-optimal minima. As an outcome, HNN-2SAT and HNN-3SAT recalled a wrong model for the transistor state. The concept are similar to the global minima solutions in the neural network done by Sathasivam [3, 24]. As the number of neurons increased, the global minima ratio will decreased. Same goes to our proposed algorithm. When the VLSI models get more complex (higher number of transistors), the number of correct or functional circuit will decreased. It is obvious that the number of correct VLSI models are reduced significantly when the number of transistor increased.

• B.    Circuit Accuracy

In this study, circuit accuracy is computed based on the percentage of correctness for the recalled VLSI models from the Hopfield’s Content Addressable Memory (CAM).

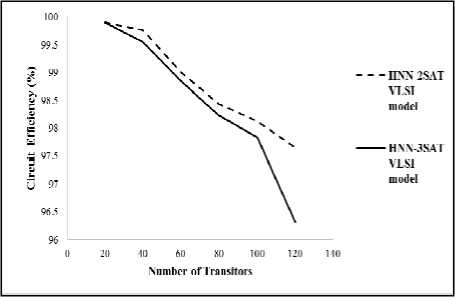
Fig.4. Circuit Efficiency for HNN-2SAT and HNN-3SAT VLSI model

Figure 4 depicts that HNN-2SAT and HNN-3SAT are able to retrieve greater than 95% correct model. Hence, the proposed algorithms can be used in reconstructing more complex VLSI models. This is because the retrieval power for both models are slightly consistent even though the number of transistors increased. The correctness of the output will be almost 100%. Relatively high circuit efficiency shows that, HNN-2SAT and HNN-3SAT has a greater stability when more transistors are introduced. In addition, better efficiency will improve the functionality of normal VLSI circuit as the complexity increases. The efficient learning algorithm will help to reduce the complexity of the algorithm. In our study, it can be clearly seen that HNN-2SAT and HNN-3SAT can be implemented as complex VLSI models. Thus, the circuit miss rate can be minimized.

• C.    Circuit Runtime

Circuit runtime is another indicator to check the effectiveness of VLSI models. The performance of VLSI models can be determined via the time taken for the circuit to fully functional. Theoretically, as the number of transistors in VLSI model increases, the circuit runtime will increases.

Table 3. Circuit Runtime for HNN-2SAT and HNN-3SAT VLSI models

Number of Transistors	HNN-2SAT VLSI Models (seconds)	HNN-3SAT VLSI Models (seconds)
20	10	8
40	33	24
60	85	69
80	205	188
100	2345	2002
120	9880	7655

Table 3 depicts the runtime of the circuit with different number of transistors for HNN-2SAT AND HNN-3SAT VLSI model. It can be seen clearly that, if the number of transistor or switch is lesser, the circuit runtime is basically faster. This is due to the less burden to generate the output correspond to 5V for each of clauses or transistors. In other words, the complexity of the circuit affects the runtime for the VLSI models. The concept is related to the neurons in Hopfield logic programming. The complexity of the network increased as the network gets enormous. Hence, this is because of a condition when the network getting larger and complex, the network is likely to get stuck in local minima and consume more computation time. As a result, more runtime is needed to relax to global solution as the number of neurons increased. The neurons need to jump massive energy barrier to reach the global solutions.

According to our HNN-2SAT and HNN-3SAT VLSI circuit, we observed that the runtime for the circuit is directly proportional to the number of transistor. This key active electronic component is vital to ensure the circuit to be operated properly. Most of the runtime spent during the process of producing 5V output in each clauses for every VLSI models. If the transistor combination doesn’t satisfied, the final output will be 0V and the overall VLSI model will function improperly. In our study, if the number of these active electronic components are exceeding 120, the circuit need more runtime before it can be declared functional. All in all, complex circuit will consume time in order to complete the operation or in our cases to be satisfied. Better optimization technique can be applied to improve the circuit runtime for highly complex VLSI models.

• VII.    Conclusion

We have presented our proposed algorithms, namely HNN-2SAT and HNN-3SAT VLSI models to check the VLSI circuit correctness if the number of transistors gets higher. It had been shown by the computer simulations our proposed models that incorporated with Hopfield neural networks were able to retrieve the desired output as the traditional VLSI models did. Hence, the proposed models are supported by the very good agreement of global VLSI configuration, circuit accuracy and circuit runtime obtained. Thus, our models can be integrated to solve more complicated electronics problem.