Внешние барицентрические координаты для произвольных многоугольников и приближенный метод их вычисления

Теоретическое изучение колебательно-волновых процессов неизбежно связано с исследованием соответствующих краевых и начально краевых задач математической физики [1–4]. Одним из вычислительно эффективных методов их численного решения является барицентрический метод (БМ) [3]. С учетом выделенных в работах [4–9] алгоритмических особенностей реализаций вычислительная эффективность БМ основывается на формировании глобальной системы базисных функций для заданной области анализа Q , граница ∂Ω которой параметризуется в кусочно-линейном представлении. Глобальные для Ω базисные функции составляются [6] с применением классических интерполяционных методов [5] в вводимой для Ω барицентрической системы координат [10–13]. Относительно простое аналитическое соотношение, позволяющее с заданной точностью составлять для Qc К ² барицентрическую систему координат, получено в [13].

В целом текущие математические представления БМ [3–13] определяют его вычислительно

эффективную применимость относительно численного решения внутренних краевых и начально краевых задач математической физики. Одно из направлений развития БМ состоит в формировании теоретических решений, унифицирующих его относительно исследования внешних краевых и начально краевых задач математической физики. Первичный этап в получении подобных решения состоит в введении понятия внешних барицентрических координат для Q , задаваемой произвольной многоугольной областью, и формировании простого аналитического соотношения, позволяющего с заданной точностью составлять для К ² \ Q ( Q = QudQ ) барицентрическую систему координат.

Получение указанных теоретических решений составляет цель настоящей статьи. В основу их формирования положим результаты [13–15].

• 1.    Постановка задачи

Пусть Q c К ² : 0 eQ - односвязная область, ограниченная замкнутой ломаной линией без самопересечений при

N - d’ Ur i, i=0

где

• ^г i = { ^x i ( t ) = e i t + P i , t ^e[ 0, 1 ] } ;

• e i = P i + 1mod N - P i ,

{ P o , P i ,..., P n - 1 } - множество неповторяющихся вершин Q , нумерация которых определена в порядке положительного обхода Q [16].

Определение 1. Внешними барицентрическими координатами Z i для Q назовем набор Z = ( Z i ) n функций Z i ( x ) e [ 0,1 ] ( x e К 2 \ ’ ) , которые удов-

• ^u i ( t ) = ^{2 U} i ( ^x j ( t ) ) ;

Kjk (t, s) - ядро интегрального уравнения (4), которое с учетом [13; 14] при t, s e [0,1] определяется соотношением

2| ek\ -п^{- 1} x

K jk ⁽ t , s н ^x Im L e k / ( e k s + P k ^- e j t ^- P j )

j * k ;

• ² e k i, j = k .

Решение интегрального уравнения (4) относительно ф j ( t ) позволяет задать Z i ( x ) при вычислении интеграла:

летворяют условиям :

• AZ i ( x ) , x e К ² \ Q ;

• ^Z i ( x ) = t , x ^er i - i ;

• ^Z i ( x ) = ^{1 -} t , x ^er i ;

^Z i ( x ) = 0, x cd’ \ { r i — I , г i } .

N - 1¹

^Z i ( ^x ) = Е j ^ф j ( t ) H j ( t ’ ^x ) ^dt ’                         ⁽⁶⁾

j = 0 0

где

H j ( t ’ x ) =| e j |^{- Im} L e j /( e j t ⁺ P j ^- x ) ] /^{2 п} .             (7)

Решение внешней задачи Дирихле (1) по аналогии с [13] выполним известным методом Фредгольма при представлении функции Z i ( x ) в виде логарифмического потенциала двойного слоя [15, с. 93]:

2. Приближенно аналитическое определение внешних барицентрических координат

^Z i ( ^x ) = J ^ф i ( У ) dQ

1 d In | x - y| 2 n   dv y

dl y ,

где x e К ² \ Q ; d^v _y - частная производная по внутренней нормали v у к 5Q в точке y e dQ ; dl y - дифференциал кривой 5Q ; Ф i ( у ) - неиз

Решение интегрального уравнения (4) по аналогии с [13; 14] предполагается выполнить с применением формулы Гейне [17, с. 169] при разложении ядра K jk ( t , s ) в виде

ГС

K jk ( t , s ) =¹ 0 ^k ( t ) + Е ( ² n + 1 ) ¹ n ^k ( t ) L n ( ² s - 1 ) ;      (8)

n = 1

вестная плотность на границе 5Q области Q ,

однозначно определяемая из интегрального уравнения Фредгольма II рода [13, с. 93]:

I e k l^{+п 1 x}

/ \            t \       1 ⁵ ln| x - у|

^Ф i ( x ^{)+ 2} ( ^Ф i ( ^y ) ^{1 -} — 5Q L               ^y .

¹ 0 k ⁽ t ) = ² <^x Im ^[ Q 0 ( ² ( e j t + R jk ) /ek ^- 1 ) ] , ^j * k ,

x edQ , i = 0, N - 1.

dl y = 2U i ( x )

| e k |, ^j = ^{k ;}

1 n ^k ( t ) =

В выражении (3) через U i ( x ) обозначены заданные в (1) значения Z i ( x ) на 5Q .

Следуя результатам [13; 14], для удобства представления решения задачи (2), (3) построим Q с С : 0 eQ на комплексной плоскости С . При этом, с учетом параметризации 5Q и граничных условий из (1), интегральное уравнение (3) запи-

² *^{- 1} Im [ Q n ( 2 ( e j t + R jk ) /e k - 1 ) ] , j * ^k , 0, ^j = k ;

шем в виде

N - 1 ¹

Ф ij ( t ) ⁺ Е J Ф k ( s ) K jk ( t , s ) ^ds = u i ( t ) ,                 ⁽⁴⁾

k = 0 0

где

j = 0, N - 1; ф ij ( t ) = Ф i ( x j ( t ) ) ;

n > 0, где Rjk = Pj - Pk; Ln (т) и Qn (z) - многочлены Лежандра первого и второго рода соответственно, задаваемые с учетом известных [14; 17; 18] рекуррентных соотношений.

Разложение (8) ядра (5) интегрального уравнения (4) на две системы линейно независимых интегрируемых с квадратом функций { 1 nk ( t )}, { L n (2 s - 1)} ( n = 0,1,...) и результаты лемм [13] позволяют задать приближенно аналитическое решение внешней задачи Дирихле (1) при введении следующих представлений.

Неизвестную функцию плотности ф j ( t ) в интегральном уравнении (4) формализуем выражением

N-1 ® ф i (t)=uj (t)- EE Sin ^^+1x nk (t),           (9)

k = 0 n = 0

где

S kn = V2 n + i / ф k ( s ) L n ( 2 s - 1 ) ds •                  (10)

Определение S_kⁱ_n выполним, применив метод PG-ядер [19], в котором при подстановке (9) в (4) задачу нахождения коэффициентов S_kⁱ_n сведем к решению системы линейных алгебраических уравнений (СЛАУ):

S i ( E + T ) = U i ,                                       (11)

где E – единичная матрица размера

[ N ( M + 1 ) ]x[ N ( M + 1 ) ] ;

T – блочная матрица, составленная из элементов

T nm = ^ n + 1 +2++\ J x m ( t ) L n ( 2 1 - 1 ) dt

( n, m = 0,1,...);

S ⁱ – блочный вектор искомых коэффициентов разложения S ^n ; U i - блочный вектор, сформированный элементами [13]:

U n = ^' n - 1 J u k ( t ) L n ( 2 1 - 1 ) dt =                   (12)

1, ( i = k v i = k - 1 ) a n = 0,

• - 143 , i = k a n = 1,

• 143 , i = k - 1 a n = 1,

• 0, иначе.

Вычисление

Tnm=^n+i 424+1 jx mk (t) Ln (21 -1) dt может быть выполнено аналитически с применением результатов лемм [14] или численно по квадратурному методу Гаусса – Лежандра [3].

Перепишем уравнение (4) в операторной форме:

ф i + £ ф i = u i ,                                      (13)

где ф i = ( ф ij ) _N ; u i = ( u j ) _N ; £ = ( £ _jk ) _{N x N} - матричный оператор;

X N - 1          N - 1

£ ф i = E £ k ф k ;...; E £ n - 1 k ф ⁱ _: ;

₄ k = 0              k = 0

( £ jk ф k ) ( t ) ^E j K jk ( t , ^s ) ф k ( ^s d^s

– линейный ограниченный оператор на пространстве функций из C ([0,1]) [13; 14].

Следуя [13; 14], введем в рассмотрение линейный ограниченный оператор:

(£M ф k)(t>

E (2 n + 1)X nk (t )J ф k ( s ) Ln (2 s - 1)ds, n=00

и определим уравнение:

ф M + £M ф M = u i,(15)

где ф M = ( ф jM ) n обозначает приближение функции плотности ф j выражением (9) при замене бесконечной суммы по индексу n конечной с ограничением числа слагаемых до M .

C применением формулы Гейне [17, с. 169] запишем разложение (7) в виде

H j ⁽ t , x ) =Ы^- ₂ П ^Im e j ⁽ e j t ⁺ P j ^- x )

- 1

E ( ² n + 1 ) ^x n ( x ) L n ( ² 1 - 1 ) ;

n = 0

xj (^ Jej | + ^ Im [Qn (2 (x - Pj )/ej - 1)], n = 0; V1 Im [Qn (2 (x - Pj )/ej - 1)] , n > 0, для которого введем в рассмотрение операторы [14]:

N - 1 ¹

(^фi)(x)"Ej Hj (t,x)фj (t)dt;(17)

j = 0 0

( H ^M ф i ) ( x ) =

N-1 L ®

E ^ - E ( ² n + 1 ) ^X n ( x ) J L n ( ² 1 - 1 ) ф ij ( t dt :

j=0 p n=0

Обозначим единичный оператор символом I .

Уточним определение норм некоторой векторной функции ф = ( ф j ) n в пространствах C ([0,1]) и L ₂ ([0,1]) [19]:

II ^ф1 И с = max i] 1^ф j ⁽ t )^; W L 2 j e{0, N -1}

¹ n - 11          2

4 Ej ^[ф j ⁽ t ^{)] dt} . ⁽¹⁸⁾ \ j = 0 0

Для введенных представлений сформулируем основной результат настоящей статьи следующим утверждением.

Теорема 1. 3 M e N : V M >  M решение

N - 1 M ____

Z M ( x ) = EE^ 1 n ( x ) S kn

j = 0 n = 0

внешней задачи Дирихле (1) существует и единственно, при этом справедливы оценки :

Учитывая представления (8), (9), (19), результаты [13; 14] для заданной параметризации 5Q и Z j ( x ) <  1 при x e R ² \ Q , установим справедливость следующих неравенств:

I^Z M -^Z < 1

< const max 2 га- ¹ + e

I C           j e { 0 N - 1 } { j ¹ j }

X

I p«I I c

X

( M + 0,5 ) ¹ + ( M + 1,5 ) ¹

I^Z M -^Z < L

= const M 2 ^M x

x(2M +1) 1 (2M + 3) 1/2 , где const – положительна и не зависит от M.

В выражениях (19)–(21) приняты обозначения [13; 14]:

= max tем N b xeR2\Q < max je{0, N-1 < max ej

■ } je{0, N-1}

Г.

^{2 p(} t ) ej|

\

+ —

e j

-

± Im 2 n

max

ⁿ x e R ² \ Q

+ min j e { 0, N - 1

’ ■ = min

.    I |sin a j j ,

a j e ( 0, П 2 ) с ( 3 л/ 2,2 п ) ,

a j e

a j - внутренний угол Q при вершине P j .

Доказательство. Подставив разложение (16) в (6), получим

да

N - 1       ¹

z i ( x ) = E ( ² n + RE ¹ n ( x ) b j ( t ) L n ( ² 1 - 1 ) dt • (22)

n = 0

j = 0

Принимая во внимание (10), перепишем (22) в виде

N - 1 да

Z j ( x ) = EE V2 n 7i1 n ( x ) S kn .

ej

"IA

e j t + P j - x J^

N - 1 ¹

E j = 0 0

ej^t -12 ejt + Pj - x dt <

ai

— +1;

¹R 2 ⁿ

II⁵ M I C    ^{p 1+ к M} u i

< 2

i + к ^M R¹

p ( н M - н )

<

C

N - 11

< max_ E x e ^R 2 \^Q j = 0 0

^X L n ^{( 2} t ^{- 1 )-}

< const 2 n

<

<

C

= const

C

max 2wd + e ; j e { 0, N - 1 } { j ¹ j }

^p( t ) 2 n

^ да

E ( ² n + 1 ) Q n

₄ n = 0

ej

x - e-t + P- j j 2

<

( M + 0,5 ) ¹ + ( M + 1,5 ) ¹

x - P 2 ^j

e

-

1 X

•

j = 0 n = 0

Из [21, с. 76] го оператора К ( I + К ) ^-1 ввиду

X

его ядра. Указанное обеспечивает разрешимость

уравнения (13) в виде ф i = ( I + К )

¹ u ⁱ и с учетом

1 5 M - 4 i ^{s const} max-,12 ’-¹ +| e j |i

^C           j e { 0, N - 1 }

X известно, что для интегрально-существует обратный оператор справедливости разложения (8)

	p ( К - К M )		C	p ( I + К ) 1		2 C
1 -		p ( I + К ) 1		C	p ( К - К M )		C

•

справедливости (23) определяет существование и единственность решения (19) внешней задачи Дирихле (1) для M ^ да . Принимая во внимание результаты доказательства теоремы 2 в [14], определим следующую оценку в C ([0,1]):

Принимая во внимание результаты [13; 14]

для

I^z M -^Z i l <иidd m — ? i n.

I C ⁺

+

II ⁵ m H ^p( ^{н M} - ^н H I •

(24)–(28), окончательно определим справедливость оценки (20), что и требовалось доказать относительно полиномиальной сходимости в C ([0,1]) решения (19) внешней задачи Дирихле (1).

С учетом результатов [13; 14] и полученных соотношений (25)–(28) зададим следующие оценки в L ₂ ([0,1]):

где ф i = ^d i p , ф M = ^d M p , p = p ( t ) = 27 t - t ^{2 -}вая функция [13].

весо-

II^z M -M L <и l h m - ⁵ i ll

I L ₂ ⁺

+

II ⁵ M l, И ^{н M} - ^н )

;

L ₂

I pH. 1⁵ M l

- const;

L ₂

- const;

C

p ( H M - h )

- 1 const M 2 ^{- M}

C ( 2 M + 1 ) 4 2 M + 3

;

p ( К - £ ^M

- const-----------

1 - p ( I + £ )

)   p(1+£)

L ₂

- 1

L ₂

- 1

L ₂

p ( £ - £ ^M )

L ₂

- 1 const M 2 ^{- M}

--------------------------------1                            •

( 2 M + 1 ) V2 M + 3

Принимая во внимание результаты [13; 14] для (29)–(33), окончательно определим справедливость оценки (21), что и требовалось доказать относительно экспоненциальной сходимости в L 2 ([0,1]) решения (19) внешней задачи Дирихле (1). Теорема доказана.

P8 := r V 11.5 ^ 9.5 7 P9 := ( V 6.5 10.5 7 , P10 := 6.5 12 7 , P11 := ( 8 л 13 V 7 ’ P12 := ( 9.5' 15.5 , P13 : ( 9 " 16 , P14 : = (8.5 ^ 17 , P15 := ( 8 л 18 , P16 := V (6.5' 18.5 7 , P17 : V 7 (51 18 , P18 : = 7 4.5 ^ 17 , P19 := V 7 (4' 16 , P20 := P23 := P26 := P29 := – дл V (3.5' 15.5 V ( 5.5' 10.5 V <5 5^1 9.5 V 7 (4.5 ^ 1 V 7 я вы ^ , P21 := ^ , P24 := P27 := P30 := полнен Г V r V и ( 4 1 J V 3.. 4. 6' 4 ? я .57 3 .5 .5 5" 5 J , у ’ P22 , P25 7 , P28 : P31 := словия = \ 17 V 7 ( 5.5" 12 V (1.5 6 V 3.5 ^ 1 7 ^ ; 7 □ c' • ^ 7, , R2 : 0 ef V ос у- ществляется центрирование точек:

^*

P

3. Алгоритмическая реализация вычисления внешних барицентрических координат и тестовые примеры

1 N - ¹     ( 6.515625 ^

_N ^ ^Pi = 9.546875 i = 0       V           7

P j ^: = P j ^- P ;

Для наглядной демонстрации предпочтительности, работоспособности предложенного решения, а также с целью выделения общих алгоритмических особенностей практической реализации

приведем структурированные псевдокоды программы вычисления внешних барицентрических координат, сформированные с синтаксисом преимущественно для САПР MathCad. Также для наглядности представим результаты работы программы в САПР MathCad на произвольном

- построение Q на С и определение элементов, применяемых для параметризации 5Q :

^{Z : =} ( P j ) 0 + i ( P ) 1 , e j ^:= z mod ( j + 1, N ) - z j ,

R ij ^: = z i ^- z j .

2. Формирование вспомогательных вычислительных функций:

– рекуррентное вычисление многочленов Лежандра первого и второго рода:

L ( x , n ) : = if n = - 1

then return 0

многоугольнике.

Псевдокоды программы отразим поэтапным решением, взаимосвязанным с материалом пп. 1 и 2.

• 1.    Задание Q многоугольной областью:

• - число вершин и индексы: N : = 32, i : = 0.. N - 1, j : = 0.. N - 1;

  – положение вершин с нумерацией в порядке положительного обхода Ω:

else if n = 0

then return 1

else if n = 1

then return x else

P o : =

( 10 'I

, P 1 : =

( 10 ^

2.5 ’

P 2 : =

( 8 'I

V 7

, P 3 : =

( 8 ^

5 ’

P 4 : =

( 6.5 ^

8.5

V 7

, P 5 : =

( 10.5 ^

, P 6 : =

( 8 'I

, P 7 : =

5 ’

p 0 ^ 1

p 1 ^ x for i ^ 1 to n -1 do

( 2 i + 1 ) - x ■ p 1 - i ■ p 0

p ^------------- i + 1

p 0 ^ p 1

p1 ^ p return p

Q ( x , n ) : = if n = - 1 then return 1 - 0.5 In ( 1 - x ² ) else if n = 0

then return arccoth ( x )

else if n = 1

then return x arccoth ( x ) - 1

else p0 ^ arccoth (x)

p 1 ^ x arccoth ( x ) - 1

for i ^ 1 to n - 1 do

( 2 i + 1 ) - x ■ p 1 - i ■ p 0

p ^<           i + 1

p 0 ^ p 1

p1 ^ p return p

– ядро (5) интегрального уравнения (4):

² e k l^- 7 Im

K ( t , s , j , k ) : =|         ⁿ

2|ek\, ek eks + Zk - ejt- Zj

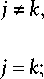
– разложение (8) ядра (5) для заданного M (для примера положим M : = 4):

X(t, j, k, n) := if j = k then if n = 0

then return 2 ek else return 0

else if n = 0

then r ^ r + ej return r

M

H (j, t, x) := УД 2 n +1)1( j, n, x) L (21 -1, n)], n=0

H ( 1,0.2,0.1 + 0.2 i ) = 2.1025188715423075,

H ( 1,0.2,0.1 + 0.2 i ) = 2.102518880606145;

– элементы T_n^j_m^k блочной матрицы T в составляемой СЛАУ:

T (j, k, n, m) = 4 2 n +1V 2 m +1 x x |x(t, j,k,m)L(21-1,n)dt;

– вспомогательная функция определения индекса в диапазоне от [ 0; N - 1 \ и элементы U k _n блочного вектора U ⁱ , вычисляемые по правилу (12):

U (k, i, n) := if k = i then if n = 0

then return 1

else if n = 1 then return - 1/^3

else return 0

else if k = sp ( i - 1, N )

then if n = 0

then return 1

else if n = 1 then return 1/V3

else return 0

else return 0

r ^ Im n

e -t + R^ q 2 ^---- j ^k - 1, n

[       ^e k

if n = 0

then r ^ r + ek| return 2r

M

K ( t , s , j , k ) : = ^ [ ( 2 n + 1 ) x ( t , i , j , n ) L ( 2 s - 1, n n = 0

K ( 0.2,0.8,1,3 ) = 7.630364353568128,

K ( 0.2,0.8,1,3 ) = 7.630398154688569;

- функция H j ( t , x ) в (7):

H ⁽ j , t , ^x ) ^:= | ^ej|

-

1 _Im

2 n

j e j t + Z j

;

-

- разложение (16) функции H j ( t , x ) :

n

Г x - Z;

Q 2---- j

e

-

Yl

1, n

sp ( i , n )

mod ( i , n ) , mod ( n + i , n ) ,

i > 0, i < 0.

3. Составление СЛАУ (11) и ее решение при S_kⁱ_n :

– число элементов в блочных векторах и матрицах составляемой СЛАУ:

NM : = N ( M + 1 ) = 160;

– вычисление T и U ⁱ :

T : = for q ^ 0 to NM - 1 do

j ^ ceil

q + 1

M + 1

- 1

n ^ mod ( q , M + 1 )

for g ^ 0 to NM -1 do k ^ ceil g + 1 |-1

^ M + 1 J

m ^ mod ( g , M + 1 ) T qg = T ( ^{j ,} k ^, n ^, m )

return T

M = 1

M = 3

M = 5

Рис. 1. Результаты расчета Z 1 ( x ) для ^

Fig. 1. Calculation results of Z i ( x ) for ^

M = 7

U i : = for q e 0 to NM - 1 do

j e ceil

q + 1

M + 1

- 1

4. Вычисленная функция плотности ф j ( t ) по правилу (9):

2 ( 1 - 1 ) , i = j ,

n e mod ( q , M + 1 ) f_q = U ( k, i , n )

return f

u ( i , j , t ) : = <  2 1 ,

0,

sP ( i ^- 1, N ) = j , otherwise;

– формирование единичной матрицы E и решение СЛАУ (11) при определении S_kⁱ_n :

E : = diag ( 1 ) ; S i : = ( E + T ) - 1 U i ;

S i : = for q e 0 to NM - 1 do

N - 1 M _____ .

ф ( i , j , t ) : = u ( i , j , t ) - ^£ ^V 2 n + 1 Ц t , j , k , n ) S^l_kn j ;

k = 0 n = 0

j ^ ceil

q + 1

M + 1

- 1

n e mod ( q , M + 1 )

q - S i Sjn = Sq return S

5. Определение внешних барицентрических координат по правилу (19):

N - 1 M

^Z ( i ^, x ) : = EE [^ n ⁷¹4 j ^, n ^, x ) S jn ] .

j = 0 n = 0

На рис. 1 приведены результаты расчета линий уровня внешней барицентрической координаты (БК) Z 1 ( x ) для рассматриваемого в приведенном листинге Q при различных M .

^Z 3 ( x )

Z5 ( x )

« 7 ( x )

Рис. 2. Результаты расчета Z i ( x ) для Q при M = 7

Fig. 2. Calculation results of Z i ( x ) for Q at M = 7

^Z 16 ⁽ x )

На рис. 2 показаны результаты расчета линий уровня различных внешних БК для рассматриваемого в приведенном листинге Q .

Заключение

Сформированное решение позволяет с экспоненциальной скоростью сходимости и высокой вычислительной устойчивостью определять внешние барицентрические координаты для произвольных многоугольников. Высокая точность полученного приближенно аналитического решения обеспечивает нахождение внешних барицентрических координат для M е[ 5;8 ] . Прочие достоинства заданного решения соответствуют выводам [13].

Главный результат настоящей статьи состоит в формировании теоретического решения, составляющего исходную основу для задания глобальных базисных функций в К ² \ Q при численном решении внешних краевых и начально краевых задач математической физики в приближении барицентрического метода. Автор статьи считает, что приведенные подробные результаты алгоритмической реализации вычисления внешних барицентрических координат вызовут интерес и сделают материал публикации доступнее широкому кругу читателей, позволят просто интерпретировать текущий результат в практическую реализацию решений [13; 14] и приведут к развитию барицентрического метода в направлениях, указанных в настоящей публикации, а также в работах [3; 22].