Внешние и внутренние гидродинамические поля, создаваемые взаимодействующими неоднородными пористыми частицами

Для расчета сил взаимодействия случайной совокупности из непроницаемых сферических частиц с однородным потоком жидкости в стоксовом приближении (Re <С 1) Тэм в работе [1] предложил метод «точечных» сил. Обобщая этот метод, в работе [2] были получены выражения гидродинамических полей в случае обтекания неподвижных однородных изотропных тел пористости е и постоянной проницаемости к. В настоящем исследовании проведено дальнейшее обобщение этой же постановки и считается, что пористая структура частиц радиально-неоднородна (е, к — функции от радиуса частиц). Далее мы полагаем, что частицы неподвижны и расположены случайным образом, а их объемная концентрация не велика (/ < 0,1).

Уравнения в приводимой ниже постановке обезразмерены, в качестве характерных масштабов длины, скорости и давления выбраны соответственно величины: а — характерный радиус частиц, U_o — среднерасходная скорость набегающего потока, ро = pU^/a, где р — динамическая вязкость жидкости.

Внешнее стесненное движение несжимаемой жидкости описывается уравнениями:

• ■               AV-a²V = VP, V-V = 0,                  (1)

где V и Р — усредненные по ансамблю частиц скорость и давление жидкости, а —- параметр, учитывающий стесненность течения. Пусть на отдельную пробную частицу, выделенную из совокупности, в направлении потока со стороны жидкости действует сила:

F = P(a,/c)i,                                   (2)

тогда параметр cv в уравнении (1) определяется условием самосогласованное.™ задачи: а² = j n(a)D(a, k)da,                          (3)

где п(а) — счетная концентрация частиц. Счетная концентрация, коэффициент проницаемости и параметр а в задаче обезразмерены следующим образом: п* = па^, к* = ко², а* = аа"¹. Сила в формуле (2) обезразмерена на 6ivpaU₀.

Фильтрационное течение жидкости внутри частицы описывается системой уравнений Дарси:

v = — k(r)Vp, V ■ v = О,

где v и р — фильтрационная (расходная) скорость и давление.

Граничные условия для нормальной и касательной компонент скорости и давления на поверхности пористой частицы, в сферической системе координат, помещенной в центр пробной частицы, имеют вид [4]:

V_r = v_r, V₉-y_e = xVk^, Р-2^=р,           (5)

где А — безразмерный параметр, зависящий от физической природы пористого материала частицы и от геометрии ее поверхности. Вторая формула в (5) справедлива только для очень малых значений коэффициента проницаемости на границе.

Согласно [1], решение внешней задачи имеет вид

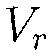
(г³ — 2В — 2А(1 + ar)exp(—ar)) cos#,

P=—a²(l + Br ³)rcos#,

Vg = —- (г³ + В + А(1 + ат + а²г²)ехр(—аг)) sin 9.           (6)

Для внутренней задачи в случае стационарного обтекания неоднородной пористой сферической частицы поступательным потоком, согласно работе [3], решение системы (4) можно представить в виде:

р = СЦт) cos 9, v_r = —Ck^h' (г) cos 9,

Ug = cipW)stne, (7) r

где h(r) — ограниченное при г = 0 решение уравнения: — [кг²д'У + 2кд = 0.

Явные формулы решений для гидродинамических полей получаются после нахождения коэффициентов А, В и С из граничных условий (5).

Рассмотрим эти решения на примере распределения пористости, приближенного степенной функцией. В этом случае коэффициент проницаемости имеет вид

&(г) = (к_у - к_оу^ь + к₀, (0 к₀, ^ ^ 1, Ь> 0).

Эта формула задает радиально неоднородное распределение пористости со значением коэффициента проницаемости ко в центре частицы (г = 0) и ку на ее границе (г = а). Если к₀ = к_г, то частица имеет постоянную пористость к^ = к^, если к₀ > ку, то пористость убывает от центра к периферии, если, напротив, к₀< ку, то пористость растет при удалении от центра частицы. В частном случае, когда к₀ = 0, к^ — кхт^ь, частица имеет непроницаемое ядро.

В этом случае дифференциальное уравнение для функции у(г) принимает вид:

т²((ку - к₀)т^ь + koV + ((b + 2)(/ci - ко)?*¹ + 2/сог)д' - 2((fci - к_оу^ь + к₀)д = 0.

Ограниченные решения этого уравнения можно выписать через гипергеометрическую функцию F(a, 0, 7; ж) [5]:

Цт) = г F

С*2 + 51 С2 + ^2

где By, В₂ — корни квадратного уравнения -у² — (6 + 1)у — 2 = 0, d = (к₀ — к^,к₀ . Используя данное решение, получим:

Для нахождения коэффициентов А, В, С в выражениях для скоростей и давления из краевых условий (5) имеем систему линейных уравнений:

-2(1 + с0е~^аА -2В + mh^kyC +1=0,

4(3 + За + а²)е'“А + (12 + а²)В + Ц^С + а² = 0, 2(1 + а + а² + кУ²Х(3 + За + 2а² + a-³)K“^A +

+ (1 + ЗХк^ )В + h^kyC + 1 — 0, где ку = А:(1), т = к'(1)/Ц1У Откуда

— тД-еД! + АА;^² — ку (4 — 4т + а²) — АА^а²),

В = — (2 + 2а + а² + А^^/2(3 + За + 2а³ + а³) -

— ку (6 + 6а + За² + а³ — т(6 + 6а + а² — а³ — а⁴)) +

+ Хку т^Зо? + За³ + 2а* + а")),

С = —т-Д—(2 + 2а + За2 + Хк\^03 + 6а + 8а2 + 6а3 + 2а4 + а5)), /Ц1)сго где сто = 1 + ® + 2а2 + A/ty/2(3 + За + 4а2 + 2а3) + ку(т(6 + 6а + 11а2 + а3 + а4) —

• -За²) + Amfc^3/2(18 + 18а + 21а² + 15а³ + 2а⁴ + а⁵).

Выражения (6) и (7) совместно с формулами (9), (10) и найденными коэффициентами А, В, С определяют замкнутое решение для полей скорости и давления около отдельной частицы при обтекании системы неоднородных пористых частиц однородным потоком.

Вычислим проекцию на направление набегающего потока силы сопротивления, действующей на отдельную частицу F = 2тг /Д—т_т6 sin 6 — Р cos 6) sin Odd, где т_те — усредненное по ансамблю частиц касательное напряжение на поверхности сферы

8т т 86

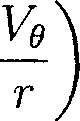
Тг0

Выражение для безразмерной силы сопротивления выглядит следующим образом:

1 6

D(a, к} = q(a, ку, Ш-Y h\XY A) = — V M^2, i=0

где <7 = /г(1)((1 + a + 2a²) + АА;У²(3 + a + 4a² 4- 2a³) + ky^o? — 3a²)) + ХкуН-'^х x (А?У²(18 + 18a + 21a² + 15a³ + 2a⁴ + a⁵) + (6 + 6a + Ila² + a³ + a⁴)).

Коэффициенты Mq-Mq тоже являются функциями от величин а, А, Л(1), h/(V), h"(l\ В силу громоздкости, явные выражения для этих коэффициентов опущены.

В случае монодисперсной суспензии (все сферы одного размера) уравнение (3) для неизвестного параметра а принимает вид a2 — nq(a, ку, ЦР), 7/(1), Ь"(ДУ А) = 0.

(П)

При 0 < А < 10, / = 4тга3п/3 < 0,1 уравнение (11), как и в случае однородных пористых частиц, имеет единственный положительный корень, а значит, и единственное значение параметра а для определения вязкого фильтрационного сопротивления.

Используя полученные формулы, были проведены расчеты для некоторых вари антов пористых частиц со степенным распределением пористости при их стесненном обтекании для различных наборов параметров ко, ку, п. При увеличении пористости

Я ПАОТПА НОГТМТТКТ Ъ^

поверхности ку, сила сопротивления незначительно растет. Этот результат одинаков при различных концентрациях частиц, а при увеличении концентрации частиц, как и ожидалось, величина силы сопротивления возрастает. Анализируя результаты, можно сказать, что наиболее значимо влияние параметра ку. Величина силы сопротивления резко уменьшается с увеличением пористости частиц на границе (увеличение ку), при этом фильтрация жидкости через частицы усиливается.

Для проведения громоздких аналитических выкладок, при вычислении коэффициентов А, В, С, М₀-М₆ и интегралов для величины F, при проверке соответствия полученных решений исходным уравнениям и граничным условиям и при решении алгебраического уравнения (И) использовалась компьютерная система символьных вычислений Maple 8.