Внутризонное магнитопоглощение сильной электромагнитной волны квантовым цилиндром

Исследовано внутризонное поглощение электромагнитного излучения большой интенсивности электронами квантового цилиндра. Найдено аналитическое выражение для коэффициента поглощения. По результатам численного анализа полученных выражений построены графики зависимости а от циклотронной частоты и частоты электромагнитной волны.

В настоящее время развитие нанотехнологий сделало возможным изготовление из слоев напряженного GaAs/GaAlAs поверхностей различной кривизны, в том числе цилиндрических поверхностей, обладающих необычными физическими свойствами [1], [2]. Особое внимание исследователей уделяется квантовым наноструктурам, конфайнмент которых можно моделировать параболическим потенциалом. Наиболее интересны оптические свойства таких структур.

Оптические электронные переходы в различных квантовых наноструктурах широко изучаются в настоящее время. В частности, межзонные переходы в квантовых ямах рассмотрены в [3], внутризонное поглощение квантовым цилиндром и квантовой проволокой исследовано в [4]. Гибридно-фононный резонанс в квазидвумерной структуре исследован в [5], многофотонный резонанс изучен в [6].

Целью данной работы является исследование внутризонного поглощения сильной электромагнитной волны квантовым цилиндром в условиях влияния магнитного поля.

Поскольку в настоящей работе рассматриваются только модели систем, описываемых параболическим потенциалом конфаймента, электрон-электронное взаимодействие не учитывается [4].

Для моделирования квантового цилиндра с тонкими стенками используем подход, предложенный в [4]. Рассмотрим 2D-электронный газ в квантовом канале с параболическим потенциалом конфаймента. Если наложить на волновую функцию электрона периодические граничные условия в одном из направлений

T(x,y)=vP(x + Z,j), где          L — длина канала, то получим модель квантового кольца конечной ширины. Модель квантового цилиндра конечной толщины получится, если добавить в электронный гамильтониан член, описывающий свободное движение вдоль оси z.

В случае цилиндра невозмущенный гамильтониан Яо одноэлектронных бесспиновых состояний будет иметь вид

Н_й = —г р--Л +--

⁰ 2т V с )      2

где

“о

т -

Р -

частота потенциала конфаймента;

эффективная масса электрона; увазиимпульс электрона.

Выберем калибровку векторного потенциала в виде Й = (- ^ДО), где В — индукция магнитного поля. Тогда, наложив периодические граничные условия по оси х, получим энергетический спектр квантового цилиндра

птр 12) 2m где Q = ^<у2 + ®2, юс = \<^В[тп с

X = г^соЦт'^а1

L = 2nR

Р

— циклотронная частота;

— энергия размерного конфаймента;

— длина канала;

— проекция квазиимпульса электрона на направление поля; m = О, ±1, ±2,...; л = 0, 1, 2, ...

Волновая функция электрона, соответствующая спектру (1), может быть записана в следующем виде

Здесь

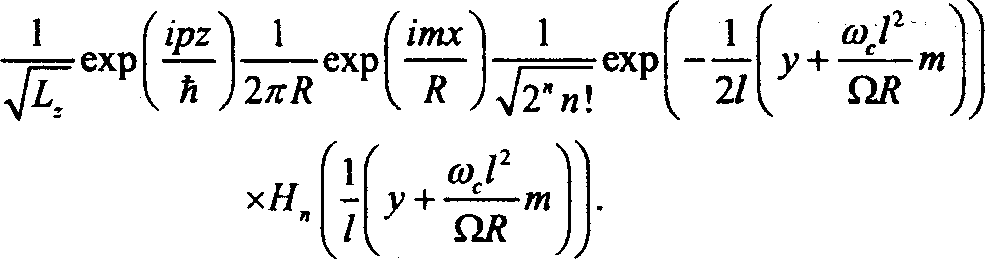
/ = Nh7m*Q, Н^ — полином Эрмита;

L_t — длина цилиндра по оси г.

Коэффициент поглощения определяется выражением тт’ пп* рр* q к

Функция распределения /у^) подчиняется следующему условию нормировки: yJv^npVp-N.

Н _т__ге „-Л

Здесь N — полное число электронов;

<о — частота фотонов.

Таким образом, с учетом (4), имеем

4л N sinh^Q/j      f i Г / j\n

/о = г ----г Z / , z\1exPl1--n + — + Ят2 + -2-г >/г\ й^пДехр^^      \  2) 2m JJ’< где ©3(х) — тета-функция Якоби;

Т — температура в энергетических единицах.

Оператор электрон-фононного взаимодействия имеет следующий вид

Здесь        H^=C^h/2a)^pV, С^ Р ЮЧ

H™x=H-exp^q?\ — константа электрон-фононного взаимодействия; — плотность кристалла; — частота фононов;

V — нормировочный объем;

q — волновой вектор фононов. ¹

Квадрат модуля матричного элемента |м|2 оператора exp(z^r) на волновых функциях (3) задается выражением

и=

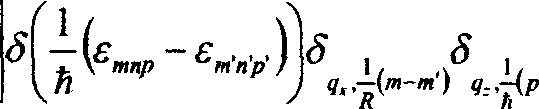
Х|^ехр2("Ф            ’Ч’ И" ” [£"7"' (2Фк ’ Чу ))J •

Здесь

ф(^3=^7- + ^-, 1 = ^Мт*^-

В случае низких температур можно считать, что электроны сосредоточены на нижнем энергетическом уровне, следовательно, в суммах по п и т можно оставить только слагаемые с п = т = 0, в сумме по к ограничимся рассмотрением членов с к = 0, ± 1.

После несложных, но довольно громоздких преобразований получим а = а0

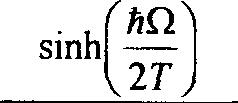
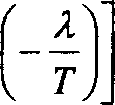
Л$2 п + — + Ат ехр ---------

V 2 J           I 2Г

Юп+Лт² +Тио Тио ----г----- ехр--^ гко 2Г

>zf>z+Am² +Тио 2Г

ЙГ>1+Ят² -Тио Тио

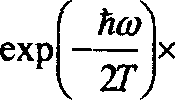
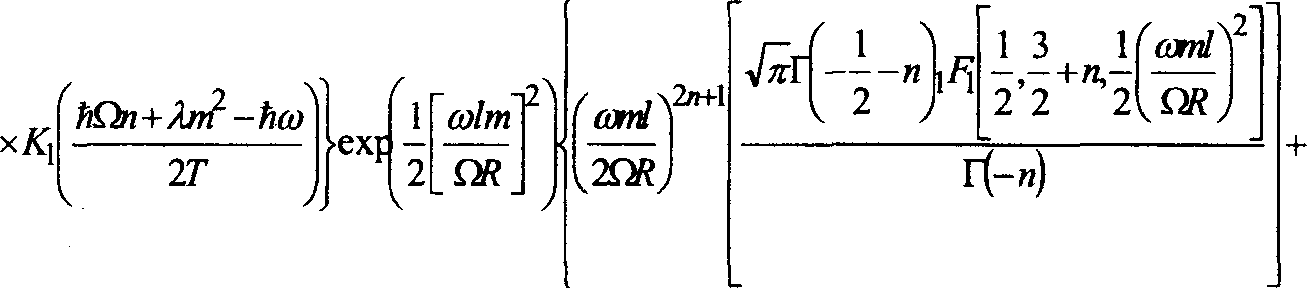
(А „     1     \(<от!У

+---;——    Г -+л LF, -п, и,— ---

( 2Q Я J V2 /      2    2 V ПК )

где

^о^^У   / Е срсо -к^гоКтг2^ \2ит Т

/,м -

Г(х) -

Kxto -

вырожденная гипергеометрическая функция; гамма-функция;

функция Макдональда.

По результатам численного анализа а по формуле (7) построены графики зависимости а/а₀ от циклотронной частоты (фактически от напряженности магнитного поля) и от частоты электромагнитного излучения, представленные на рисунках 1 и 2 соответственно.

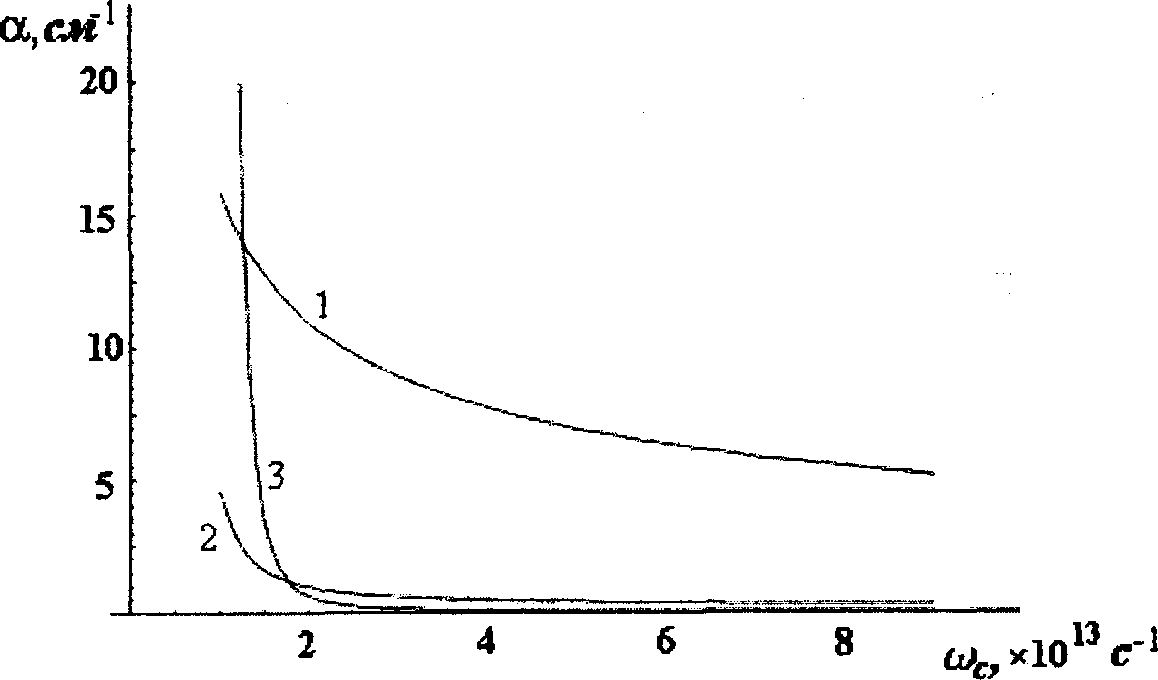
Рис. 1. График зависимости а/а0 от циклотронной частоты. Кривая 1 соответствует значению со = 0,1 • 1013с~‘, кривая 2 — со = 3 • 10'3 с !, кривая 3 — со = 6 • lO'V’1

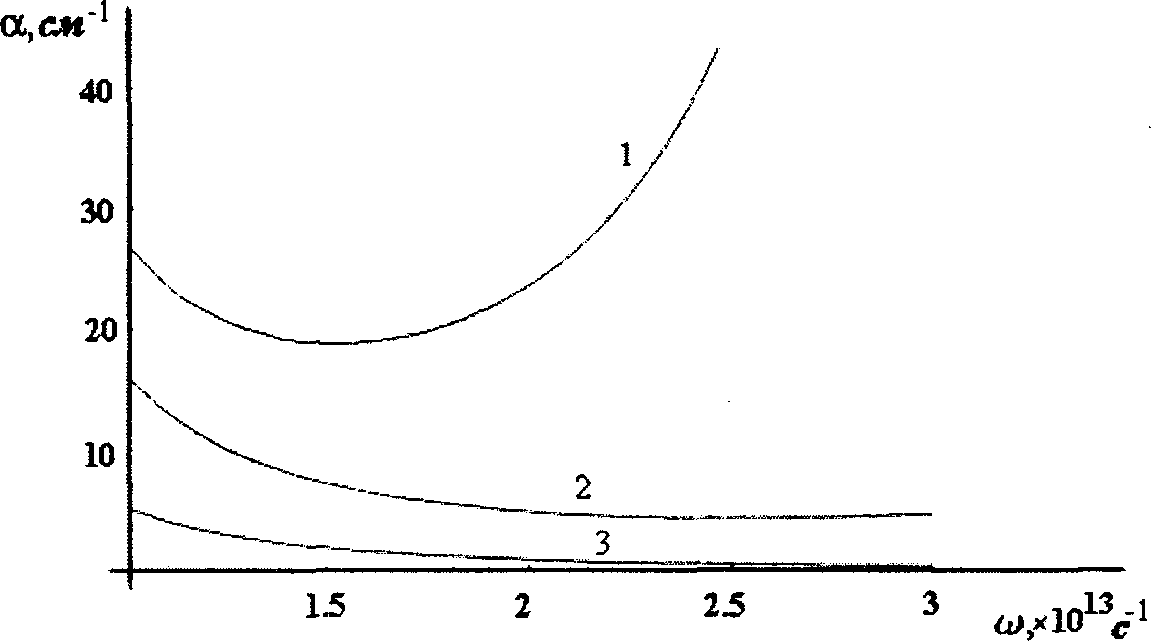
Рис. 2. Зависимость коэффициента поглощения квантового цилиндра от частоты электромагнитного излучения для ю_с= 0,1 • 10¹³с^-1 (кривая 1), 10¹³с ¹ (кривая 2), 9 • 10¹³с^-1 (кривая 3)

Для количественной оценки коэффициента поглощения используем типичные параметры сверхрешетки и квантового цилиндра: N_o= 10¹⁴ см^-3, т* = 10^-29 г, й>- = 1,6 • 10¹² с""¹, С- = 5 • 10⁸ эВ/см, Т= 1,38 • 10⁴⁵ эрг, со_о=1,6 • 10¹³с^-1, радиус цилиндра R = 10^-6 см, плотность кристалла р = 5 г/см³.