Волновое уравнение с кубической нелинейностью и возбуждение колебаний в системе "среда-источник"

Введение. Волновые уравнения с линейными и нелинейными источниками (уравнения Клейна-Гордона) являются фундаментальными уравнениями математической физики и позволяют изучать динамические свойства неравновесных состояний теплофизических, физикохимических и биологических систем [1-3]. Область практического применения уравнений Клейна–Гордона в значительной степени расширяется при учете явной зависимости функции источника от времени. Такой нелинейный реономный источник позволяет моделировать влияние внешней силы и рассматривать физически содержательные режимы воздействия на скорость и направление движения волны. Современное состояние названной проблемы и подробная библиография представлены в работах [4-8]. Отметим, что в этих исследованиях основное внимание было обращено на уравнение синус-Гордона с модификациями, относящимися к различным способам внешнего нестационарного воздействия на среду.

Цель данной статьи - построить и проанализировать точное решение волнового уравнения, для которого функция источника содержит кубическую нелинейность и явную синусную зависи- мость от времени.

Построение решения. Одномерное волновое уравнение с источником имеет вид д ² т     д ² т

"^ д(х')2 ~  ’ где т - функция, описывающая некоторое физическое свойство среды; t - время; х' = х^; x - де картова координата; w - скорость распространения малых возмущений; kи = ки (т, t) - функция источника. Для размерных и безразмерных уравнений пользуемся одинаковой формой записи, применяя масштабы тb и tb:

( ^тК ) ^ ^т , ( Фь ) ^ t , [ ^х / ( ^wtb ) ]^ ^х ', ( ^k , / h ^ть ) ^ k u •

Изолиния т(х',t) = Ti = const перемещается со скоростью N = dx/dt, которая является дозвуковой/сверхзвуковой, если число Маха M = dxУdt = N/ w меньше/больше единицы. Обозначим u = дт/дх', v = дт/дt, dт = udx' + vdt и вместо (1) запишем систему уравнений

( д v /д t ) - ( д u /д х ') = k _o , д u/д t = д ф дх’ .

После преобразования независимых переменных ( х ', t ) ^ ( т , t ) получаем [9]: д v    д v    д u ,

--+ v--u— = k,,, д t   дт   дт д u   д u    дv

--+ v— = u— • д t     дт    дт

Здесь D(т,t)]D(х',t) = дт/дх' ^ 0. Изолиния т = Ti движется со скоростью M = -v(тi,t)/u (тi,t) • Решение представим в виде u = т [ a0 + т (a1 sin kt + a2 cos kt)], v = т [bo + т(b1 sin kt + b2 cos kt)], к = const > 0 •

Шесть постоянных коэффициентов a _а, b _а, а = 0,1,2 связаны, согласно (3), следующими двумя соотношениями:

a0b1 = b0a1 - ka2, a0b2 = b0a2 + ka1 •(6)

Остальные формулы, необходимые для замыкания задачи, получаем на основе (2) при построении функции источника, вид которой определяется выражением ky = Q1т ± Q2т2 sin (kt + в) + Q3т3 (1 + a3sin2 kt).(7)

В этом случае b0 = a0 + Q1 , b2 -a12 = b22 -a2 = S3/2 ,

Q 3 a 3 = 2 ( b i b 2 - a i a 2 ) , tg в = C 2/ Q , Q 22 = C 2 + C 2 ,

C 1 = 3 ( b ₀ b 1 - a₀ a 1 ) - kb₂ , C ₂ = 3 ( b ₀ b ₂ - a ₀ a ₂ ) + kb 1 •

Физическое содержание данного решения зависит от выбора коэффициентов Q 1 , Q ₂, Q ₃. Подробные формулы для Q 2 , a 2 будут указаны в ходе дальнейших вычислений. Величина в , а также выбор знаков «+» и «-» перед Q ₂ в (7) относятся к допустимым вариантам начального ( t = 0) состояния источника. После подстановки b 1 , b ₂ из (6) в (8) получаем

⁽ a 2 ) 1,2

1 k

^b0 ^a1 ±

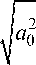
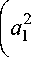
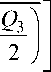
причем знак перед корнем такой же, как знак произведения b0a1. Здесь и в дальнейшем нижние индексы 1, 2 соответствуют знакам «+»/«–» перед корнем. При проведении расчетов учитываем, что a2 - a1 = 4b0ka1a2/(k2 - Q1) , a1 + a2 = a0 6з/(k2 + Q1) ,

В результате находим

2 a 23 ₌ ^{a 2} Q ³    1+       ^{4 k} 2 b ² 2Z _>0

⁽ 1       2 ( k ² + Q i ) [" ^4 a 2 k 2 + ( k 2 + Q i ) 2

Обращаем внимание на то, что здесь подкоренное выражение положительное и меньше единицы. Выбор знака перед корнем в (11) выполняется при физическом истолковании решения. Из последующих аналитических преобразований будет ясно, что выражения (10) не содержат особенность типа «деление на ноль». Связь a 2 ^ Q 2 имеет вид:

16 k ² a 2 Q 3 = ( k ² + Q i ) Q ₂ ² - Q 3 ( k ⁴ + 10 k ² Q i + 9Q 2 ) . (12)

Таким образом, аналитическая структура решения (4), (5) основана на формулах (12), (11), (9), (8) и (6). Следует отметить, что полученное решение не содержит в себе как частный случай варианты, когда Q 2 = 0 и/или a 3 = 0.

Свойства решения. Возьмем для определенности конечный интервал т е(0,тm ], τm ≡ const > 0, для которого и>0, x'е(-да,xm]. Для т < 0 рассуждения аналогичные. Принимаем естественное ограничение a2 >(a2 + a2 )Tm,                                        (13)

которое говорит о том, что sgn u = sgn( τa 0 ).

ZX/-                9      9     9        /1 AX 7 9    7 9 .7 9 TT /АХ                     7 9      9          "I—Г

Обозначим a12 = a1 + a2 , см.(10); b12 = b1 + b2 . Из (8) следует, что b12 = a12 + Q3. Представим скорость изолинии т = тi и ее закон движения следующими выражениями:

dx /dt = -[ b ₀ + b ₁₂ r _Z sin ( kt + p ₂ ) ]/[ a ₀ + a₁₀ r _Z sin ( kt + p ₁ ) ] , a ₀ >  0, b ₀ <  0, a ₁₂ >  0, b ₁₂ >  0,

x ; ( t ) . x ‘ ( r = r i , t ) = - b i t. - lln ^a 0 ^{+ a} 12 ^r z s^{in (} kt ⁺ P 1 ) + const. a ₀    a ₀       a ₀ + a ₁₂ т _Z ■ sin P ₁

Здесь tg в1 = a 2 !a\ , tg в2 = b2 P\ , cos (в1 - в2 ) = b0 a12/(a0 ^2), в1 ^ в2 • Итоговая запись функции (15) не содержит b12. Пусть x’(т = Ti,t = 0) = 0; тогда изолиния (ri + Ar)< Tm, расположенная выше (Ат>0), имеет начальную координату x’(ri + Ат,t = 0) = c0 > 0, где exp (-a0 С0 ) = T,-[a0 +(TZ- +Ат ) a12 sin Р1 ]/[(т,- +Ат)( a0 + T,-a12 sin P1 )]<1.

Анализ показал, что при всех t >0 выполнено неравенство x '( r i + А т , t ) > x ’ ( r i , t ) , которое означает, что в каждый момент времени верхняя изолиния расположена справа от нижней вдоль оси x ‘ . Следовательно, данное решение не разрушается во все время движения профиля u = u ( x ', t ) .

Если a 2 = r m a ^ , т. е. ^ r m Q 3J ( k ² + Q ₁ ) ^ = 1, то, согласно (14), в те моменты времени t = t p , когда sin ( kt + в ₁ ) = - 1, т_т - изолиния удаляется на бесконечность ( x'_m ^да ) с неограниченно большой скоростью, и исходный профиль принимает вид кинк-перехода между состояниями равновесия ( τ = 0, t ≥ 0) и ( τ = τ_m , t = t_p ). Такой режим движения можно назвать кинк-пульсациями монотонного профиля u = u ( x ', t ) >  0, рис. 1.

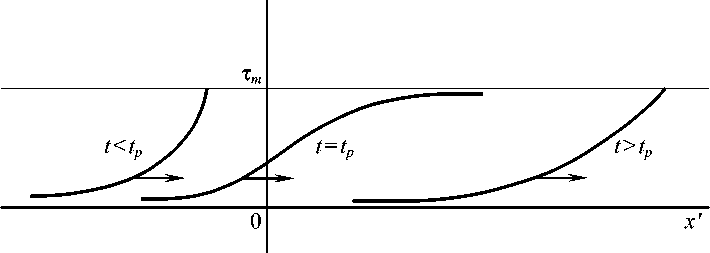
Рис. 1. Кинк-пульсации монотонного профиля. Стрелка указывает направление движения

Обсудим поведение решения в малой окрестности т = 0. При т = + 0 получаем из (4), (5) с точностью до членов первого порядка по т: т = т ₀ exp £ , Ь = a 0 x ' + b ₀ 1 <  0, a ₀ >  0, b ₀ <  0, x ' <  0, t >  0, т ₀ = const. Ясно, что эта экспонента (ангармоническое автомодельное решение) удовлетворяет уравнению d ² т/ d с ² = т, которое есть результат линеаризации (1), (7) в окрестности решения т=0. Данный вывод относится к положительным и отрицательным значениям Q₁ = b 0 - a 2 , где Q 1 - наклон функции источника к _и = Q₁ T (см. (7)). Рассмотрим изолинию т = T i = £ = + 0, где г - малое положительное число; далее для краткости называем ее е -изолинией. Для нее квадрат числа Маха равен м £ = 1 + ( Q ₁ / a 2 ) > 0, поэтому Q 1 характеризует отклонение скорости г-изолинии от скорости звука. При Q 1 < 0 эта скорость дозвуковая, при Q 1 > 0 - сверхзвуковая. Проанализируем поведение решения (4), (5), (7) при различных вариантах выбора знаков коэффициентов Q 1 и Q ₃.

Колебания высокой частоты. Допустим, что Q 1 < 0, Q ₃ > 0, k ² + Q 1 > 0. Условие (13) приводит к неравенству

0 <[ Q 3 T 2! ( к ² + Q i ) ]< 1. (16) Для удобства аналитических преобразований введем в рассмотрение вместо Q ² вспомогательный параметр m 1 :

Q2 =-16Q1Q3/(1 - m 12), 0 < m1 < 1. (17) Требование выполнения неравенства b0 = a0 + Q1 > 0 дает оценку интервала, в котором меняется частота колебаний источника (7). Обозначаем р2 = к2/(-Q1) и получаем интервал высоких час- тот

¹ <  ^Ц 2 <  ^Ц< ^Ц 1 ,

Ц 2 = ( 3 т_х + 5 )/( 1 - т_х ) , Ц 2 = ( 5 - 3 т_х )/( 1 + т_х ) .

В этом случае имеем a 2 = - Q₁ a 2 ₁,

a

2 ti

⁰¹     16 ц ²

1 - т 2

- Ц + 9

> 1,

и поэтому a 2 + a 2 в (10) не содержит к ² + Q ₁ = - Q ₁ ( Ц - 1 ) .

Порядок расчетов состоит в следующем. Указываем интервал (0, тт ], внутри которого расположена область изменения функции т (x', t). Задаем произвольно параметр источника Q1 < 0 ; выбираем значение тх е(0,1) и подсчитываем Ц, Ц2 в (19); частоту колебаний источника можем варьировать в интервале (18). Для выбранного значения р2 подсчитываем к2 + Q1 > 0, а на основе оценки (16) задаем параметр источника Q3: 0 < Q3 <[(-Q1)(4 -1)^Tm j . Определяем Q2

из (17). Коэффициент а ₃ в (7) характеризует амплитуду внешнего периодического воздействия на среду и коррелирует с частотой колебаний следующим образом:

^a 3²

= 1 +

A/u l - 4 2 4 ( — 1 ) '

При фиксированном m 1 , (см. (19)), зависимость a 3 от р ² - монотонно убывающая. Вместе с тем верхняя граница значений Q ₃ монотонно растет по мере роста р² > 1. Далее вычисляем последовательно a 2 , a 1² и ( a ₂ )₁₂ по формулам (12), (11) и (9), а также находим b 2 ; здесь в (11) был взят «-» перед корнем. Для подсчета b 1 , b ₂ и tg в применяем (6) и (8). Выбор знаков коэффициентов a ₀, a 1 , ( a ₂ ^ ₂, b о выполняем при физическом истолковании данного решения.

Итак, константа m 1 влияет опосредованным образом на ширину интервала частоты колебаний (см. (18), (19)) и на параметры Q ₂, Q ₃, а ₃ источника (см. (16), (17), (21)). Случай m 1 =1-0 оставляем в стороне, потому что он приводит к неограниченно большим значениям Q 2 и a 3 .

Пример расчета. Задаем т_т = 1, Q 1 = -1, m 1 = 1/2. Тогда 4 = 13, р 2 = 7/3 ; берем р = 2. Значит, Q 3 е ( 0,3 ) . Берем Q ₃= 1 и получаем Q 2 = 8043 , a 2 = 115/36. Далее находим a 2 = 79/64, b 2 = 1564. Числовые значения остальных констант, входящих в решение, здесь не приводятся:

эти вычисления нетрудно воспроизвести.

Обсудим возможность перемены знака скорости изолинии. Основное неравенство (16) запишем в виде 4 = 50 (-Q1)(4 -1)Jq3 , 50 «=(0,1), и тогда т2 = 50 т0, 50 е(0,1]. Скоростьт изолинии сохраняет постоянный знак, если b2 > т2b22. Это условие выполняется для изолиний с номерами Si, удовлетворяющими неравенству

50 <(a021 -1)/[50 (a21 -1 + 4 )].(22)

Здесь знак равенства относится к изолинии, скорость которой обращается в ноль в отдельные моменты времени. Скорость т i - изолинии знакопеременная, если

(a01 -1)/[50 (a01 -1 + 4 )] <52 < 1.(23)

Такие 5 ² существуют, если 5 0 не является слишком малым:

( a 0²1 ^- 1 )/( a 21 ^{- 1} + ⁴ ) < ⁵ 0 < ¹.

Поведение кривизны линии т = т (x', t) ясно из рассмотрения формулы д2т,д(x')2 = u[a0 + laaX2 sin(kt + 01)].(24)

Это выражение имеет постоянный знак, если a2 > 4/a122, т.е. (4 - 1)>^4т0Q3/(-Q1 )j. Кривизна обращается в ноль в отдельные моменты времени на изолиниях τ=τif, для которых a2 < 4T0ja02. Знак неравенства соответствует точкам перегиба, знак равенства - точка спрямле- ния, поэтому с учетом оценки (16) получаем

1 / 0 Q 3 /( - Q 1 ) ] <  ( ^{4 -} 1 ) < [ ⁴4 Q 3 / ( ^- Q 1 ) ] .

Эти неравенства совместны, если (/ 2 /4 ) <  Т 2 < / .

Колебания низкой частоты. Рассмотрим случай Q 1 < 0, Q ₃< 0, когда k ²+ Q 1 < 0. Должны быть выполнены условия b 2 = a 2 + Q 1 > 0 и ^ a 1² + ( Q ₃/ 2 ) j> 0, (см. (9)). В формуле (11) для a 1²

нужно взять  «+» перед корнем.  Итоговые оценки выглядят так:   ( к ² + Q 1 ) < Q 3 T m <  0.

Q 2 = m 2 Q 1 Q 3 . ⁹ <  m 2 <  ²⁴. a o = ^{— Q}1 ^ao i . ^ao i = ( 1 ^— Д )( m 2 ^{— 9 +} Д )/( ¹⁶ Д ) •

Низкие частоты располагаются в интервале

■² < Д 2 < ( V2 ) . ^Д = ( ^— m 2

—

m 4 + 16 m ² I /2.

В отличие от колебаний высокой частоты здесь a 2 - возрастающая функция аргумента ц²: a = 1 + ^{9 д} .

4 ('—д)

Верхняя граница значений | Q ₃| равна ( — Q 1 ) ( 1 — д ²) ^T m и убывает по мере роста частоты колебаний. Порядок расчетов аналогичен предыдущему.

Пример расчета:   т_т = 1. Q 1 = -1.   m 2 = 10.   д 3 =— 8 + V65.   ( — 19/20 ) < Q 3 < 0; берем

• ц ² = 1/20. Q ₃ = -1/10 и получаем Q 2 = 1. a 2 = 97/76 .

Условия, при которых скорость изолинии имеет постоянный либо переменный знак, записываются, соответственно, в виде (22) либо (23). Содержание этих соотношений такое: T m = 5 m Q 1 ( 1 — Д ) ]q₃ . Т = 5^ . S ² e ( 0,1 ] . 5 mm e ( 0,1 ) . Точки перегиба и точки спрямления изолиний т if появляются в отдельные моменты времени (см. обсуждение формулы (25)), если

( T m ^Q 3 / ^Q 1 ) <  ( ^{1 —} Д 2 ) ^ ( ^{4 T} f^Q3 /^Q 1 ) . ( T m /⁴ ) <  Т 2 <  ^T m .

Знак кривизны изолинии сохраняется при условии, что ( 1 — Д ) >  ( 4^Q₃ /Q 1 ) .

При очень малой частоте ц2 = + 0 наблюдается неустойчивость данного решения: a2 ~ (VД2) ^1. Ситуация меняется, если принять следующую зависимость коэффициента Q2 от частоты колебаний: m2 — 9 = m21o2. 0 < m21 Д < 15. Тогда имеем устойчивое решение:

Q ² = (9 + m ² д 2) qq . a 2, = (1 — д ²)(1 + m 2AI 16 . a ₃ ² = 1 + ° ,⁽ 1 + m 21 ) .           (27)

• ²          21Л¹ у ^1^3’  ⁰¹   \        д ²¹Л       ³           к _ д )               ^{v 7}

Здесь, как и в случае (26), a2 - возрастающая функция аргумента ц2. Далее нам понадобится интересный вариант b 1 = 0, для которого m2 — 9 = О (21д4 + 92д2 + 15)Д(5д2 +1)(1 — д2 )].

m 2 е ( 9,24 ) . Q 2² = m 2 Q 1 Q 3 . д 2 е ( 0,14 ] . 6 2 = 6 0a^ К « 0 a 2 ) .

a 21 = ( Д 4 + 6 д 2 + 1 )/( 5 д ² + 1 ) . a ^ = a 0 Q 3/ ( к ² + Q ) .                    (28)

4 ( д ⁴ + 6 д ² + 1 ) a g = 1 +-- т .

( 5 Д ² + 1 )( 1 — О ² ) 2

Отметим еще, что для рассмотренных режимов колебаний высокой и низкой частоты ( b ₀ + 0) отсутствует трансзвуковой переход вида ( М ^ 2 <  1 ) ^ ( M ² >  1 ) .

Широкий интервал частот. Перейдем к изучению варианта Q 1 > 0. Q ₃ > 0, который отличается от двух предшествующих положительностью параметра Q 1 источника: е -изолиния движется со сверхзвуковой скоростью. В этом случае Q 2 = m 2 Q 1 Q 3 . к ² = О Q 1 . ^ m Q ₃ <  ( к ² + Q 1 ) .

a

m 2 — 9 — о²

4 ( Д ² + 1 )

. m 2 >  9.

и процесс возбуждения колебаний происходит на конечном интервале частот

0 < д2 < (m2 — 9) < да . Здесь а2 - монотонно убывающая функция аргумента ц2 при фиксирован- ном m3 . Далее имеем: а0 = Q1a01, а01 = ( д +111 m3

—

9 — д ²)/(16 д ²) >  0; в формуле (11) для а 2

нужно взять «+» перед корнем; а₂ определяется выражением (9). В частности, при д ²= 1 получаем а 2 = ( m 3² — 10 )/8 > 0, а 2 = а^О зД ,

( а 2 ) 1,2 = ( 1 ± 1 ) а 01 [ О з ( 1 + а 2 ) /2 ] 1 / 2 / д .

На основе соотношений Tm = 5mQi (д2 +1)/Оз, T = SiTm, 52 е( 0,1), 52 е(0,1] находим, что скорость тi - изолинии сохраняет постоянный знак при 5^ < (1 + а^

1 + а 01 + д ² ) j . Перемена

знака происходит при ( 1 + а 2

1 + а 21 + д ² ) |< 5 ²<  1. Такое  5 ²    существует, если

[ ( 1 + а 21 )Д 1 + а 21 + д ² ) j <  5 m <  1. Трансзвуковой переход отсутствует. Условие появления точек перегиба и точек спрямления имеет вид

(д Q 3 / Q 1 ) <  ( д ² + 1 ) <  ( 4 ^т 2 ° з Q >\ ) .

Комментарий к этим оценкам такой же, как при обсуждении формул (24), (25). В случае малой частоты [ д ²=+0] данное решение неустойчивое: а 2 ~ (V д ² )»1.

Физические свойства источника (7) меняются, если считать, что коэффициент Q ₂ зависит от частоты возбуждающих колебаний. Возьмем m 2 — 9 = m 32 ₁^^L , где m 21 >  1 - фиксированный конечный параметр; тогда Q 2 = ( 9 + m 32 ₁^^L ) Q 1 Q 3 , а 2 = ( д ² + 1 )( m 2 — 1 ) /16,

a

= 1 +

д ² ( m 21 ^— 1 ) 4 ( д ² + 1 ) ’

и решение устойчивое для любого конечного д ². Теперь, в отличие от (29), а 2 - монотонно возрастающая функция д ².

При Q3 > 0 допускается случай Q 1 = 0, когда г-изолиния имеет звуковую скорость: качествен- но новых результатов здесь нет.

Задача с подвижной границей. В качестве физической модели решения (4), (5) рассмотрим процесс в полубесконечной области с неизвестной подвижной границей x ' = x W ( t ) : ( д т /d x ') >  0, ^x 'H ^{—да x}W ] , ^т Д °t _w ] c ( ° т _т ] ;

x '^—да , dTd x '^ 0, т ^ 0; x ' = x W ( t ) , ( д т/ d x ') w = g T ) ,               (31)

где Tw = t(xw,t). Функция g(tw) = g1Tw + gT характеризует зависимость градиента искомой функции от самой этой неизвестной функции; здесь g 1, g2 - положительные постоянные. Такая физическая интерпретация пригодна для всех трех рассмотренных выше вариантов: колебания высокой и низкой частоты, широкий интервал частот. Скорость движения границы равна dxw dtt = [(TwdTw/dt) — Vw]К ,

Uw = а0 + тwal 2 sin (kt + в), Vw = b0 + TAi sin (kt + A), а0 > 0, b0 < 0, а12 > 0 , b12 > 0 .

Функцию tw (t) находим из граничного условия (31) с учетом структуры решения (4): Tw =(а0 — g1)/[g2 — a12sin (kt + в1)]. Здесь следует принять 0 < g 1 < a0, g2 > a 12, и тогда Tw (t) < Tm, где Tm = (а0 — g1)/(g2 — а12) есть верхняя граница значений функции тw (t). Исходное допущение тm < тm будет выполнено, если (a0 + тma12) < (g1 + тmg2). Этому неравенству всегда можно удовлетворить подходящим выбором g2 > 0.

Колебания двух монотонных ветвей. Изучим отдельный вариант b0 = 0 (см. (8)). Формулы расчета такие:  a0 =— Q1 > 0,  a2 = a2,  a122 =— Q1Q3J(k2 + Q1),  b1 = — b2 =(—ka2 /a0), tg в = 1, a2 =(Д2 +1)2/(Д2 —1)2 . Здесь k2 =— Q^, < = ^2Q(1 - Д2)/03, ^2 <0,1) •

Колебания высокой частоты: Q 3 > 0, Q i < 0, k ²+ Q i >0, ц ² > 1, Q 2 = — m ² QQ ₃. Этот случай наблюдается при т ² > 16 для двух частот

μ ²

m ² — 6 ±

Колебания низкой частоты: Q ₃< 0, Q ₁< 0, k ² + Q ₁< 0, Q 2 = m ² QQ 3 , т ² > 9, ц ²<1,

Д ²

— 6 — т ² +

На интервале т е ( 0, т _m ] проанализируем режим колебаний двух монотонных ветвей, имеющих разные знаки наклона.

Левая ветвь: д т/ д x '> 0, a ₀ >  0, a 1 >  0, a ₂ >  0, a ₁₂ >  0 ; x ’ е ( —ж , x / ] ; x ' ^—ж , т ^ ( + 0 ) . Правая ветвь: дт/ д x '< 0, a ₀ < 0, a 1 < 0, a ₂ <  0, a ₁₂ <  0; x 'e[ x_r , ж ) ; x ^+ж , т ^ ( + 0 ) . Для обеих ветвей b 1 <  0, b₂ >  0, b 1 ₂ <  0 . Модули одноименных коэффициентов слева и справа одинаковые; tg в ₂ = — ctg в 1 ; например, далее в ₂ = в 1 + ( п/2 ) . Скорости т_т - изолиний на левой ( l ) и правой ( r ) ветвях такие:

dx ‘      dx ‘    dx;     ,  _         /Г ,    _   • л              о

—- = ^— — = — = ^{— b}12 ^т m cos ф / [ a 0 ^{+ a}12 ^т m sin ф ] , Ф = ^{kt +} P 1 .

dt      dt dt                                     ^l

Тогда закон движения тт - изолинии дается формулой xm(^ )= "^ln L a12 k

a 0 ^{+ a}12 ^т m a 0 ^{+ a}12 ^т m sin ф

, J I

Мф ) = - x ‘M = x m ( ф ) .

Качественная схема расположения монотонных профилей на плоскости ( x ', т ) представлена на рис. 2. Проанализируем поведение точек ( x ', т_т ); далее для краткости называем их т_т - точками. В моменты времени, когда ф = 2п n ₀ ( n ₀ - целое положительное число) т_т - точки на ветвях смещены влево и вправо на одинаковые расстояния от x' = 0, и их скорости направлены навстречу друг другу. При Ф = ( п /2) + 2 nn ₀, x' = 0 ветви смыкаются с нулевой скоростью и образуют слабый разрыв: при т = т_т терпит разрыв первого рода первая производная по координате. При ф = п + 2п n ₀ ветви расходятся и в последующем т_т - точки достигают наибольшего удаления от x ' = 0: ф = (3 п /2) + 2 nn ₀, см. (34). Итак, нулевую скорость т_т - изолиний на левой и правой ветвях имеем дважды в течение одного периода колебаний: в момент смыкания ветвей и в момент наибольшего их удаления друг от друга.

Обсудим пример трансзвукового перехода на т _т - изолинии при ф = 2п n ₀. В этом случае ( dx'_m (dt ) 2 = д ² § m , ^ m ^е ( 0,1 ) . Для низких частот ( ц ²<1) трансзвуковой переход отсутствует, а при р²>1 он существует, если д ² > ( 1/ § m ) . Например, для § m = 1/2 это неравенство будет выполнено, если, согласно (32), т ²> 25 (знак «+» перед корнем) либо 16 <  т ²< 25 (знак «-» перед корнем).

Теперь рассмотрим колебания двух монотонных ветвей, имеющих одинаковый знак наклона. Левая ветвь: т е (0, тm ], дт/дx'> 0, a0 > 0, a1 > 0, a2 > 0, a12 > 0, b1 < 0, b2 > 0, b12 < 0 ; x'е(—ж,x/]; x'^—ж, т ^(+0). Правая ветвь: т е[—тm,0), дт]дx'> 0, a0 < 0, a1 > 0, a2 > 0, a12 > 0, b1 > 0, b2 < 0, b12 > 0; x' e [x',ro); x’ ^ да, т ^ (-0). Скорости (±Tm)-точек противопо- ложны друг другу и вычисляются по формуле f dx' ^  _    -(b12 ) 1,r (±Tm )C0SФ

I dt J 1 , r   ( ^a0 ) l , _r + ( ^a 12 ) 1 , r (±^T m ) sin Ф "

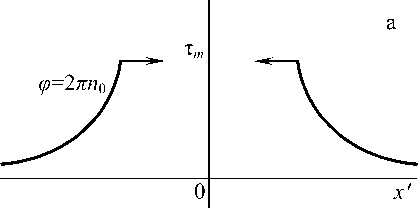
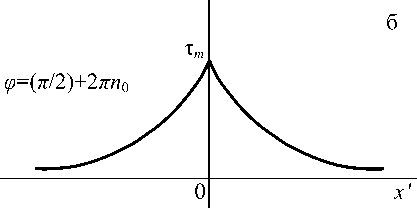
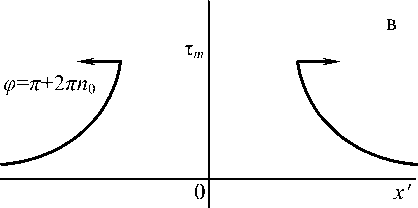
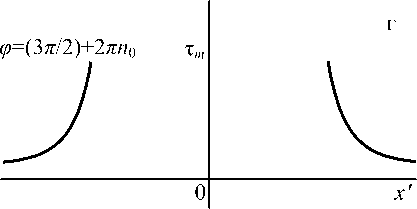
Рис. 2. Колебания двух монотонных ветвей, имеющих разные знаки наклона. Стрелка указывает направление движения

Закон движения (± T m )- изолиний дается выражением

( x') l, r

1 ^f b 12 "  k I ^a12 J l , _r

ln

^{( a} 0 ) i , r ^{+ ( a} 12 ) i , r ⁽±^T m )

( a 0 ) l , _r + ( a 12 ) l , r (±^T m ) sin Ф ’

Процесс колебаний ветвей аналогичен тому, что наблюдался для профилей с наклонами разных знаков, но теперь при ф = ( п /2) + 2 пп ₀ имеем в точке x ’ = 0 неподвижный сильный разрыв: функция т( x ’ , t ) меняется скачком от - T m до T m , рис. 3.

Для вариантов (33) и (35) корреляция «наклон ветви - скорость T m - изолинии» представляется в форме

M = ±[ ц ² F ( Z ) ] ¹² ,                                   (36)

M = dx' m /dt , Z = U m h m , F ( Z) =   [ a ², т 2m - ( Z - a 0 ) ² ]> 0•                 (37)

Две линии (36) образуют на плоскости (ζ, М ) эллипсовидную петлю динамического гистерезиса. Для левой и правой ветвей петли расположены симметрично по отношению к оси Z = 0. На рис. 4 показан качественный вид такой петли для левой ветви: Z e [ Z 1 ,Z₂ ] , Z i ₂ = a ₀ + т _m a ₁₂ •

Представляют интерес колебания на интервале (0, тj J с нестационарной границей тj = тj (t), для которой принято условие (д т/dx^. = g2 т^2, g2 = const. Возьмем ветви, имеющие наклоны разных знаков. Левая ветвь: d т/ dx1

;’j! J , т е ( 0,т j J , a ₀ >  0, a 1 >  0, a ₂ >  0 ,

a12 > 0 , b1 < 0, b2 >0, b12 < 0 , g2 > 0 . Правая ветвь: дт/dx'<0 , x'e^x’jr,да), т e(0,тj J , a0 <0, a1 < 0, a2 < 0, a12 < 0, b1 < 0, b2 > 0, b12 < 0 , g2 < 0. В данном случае

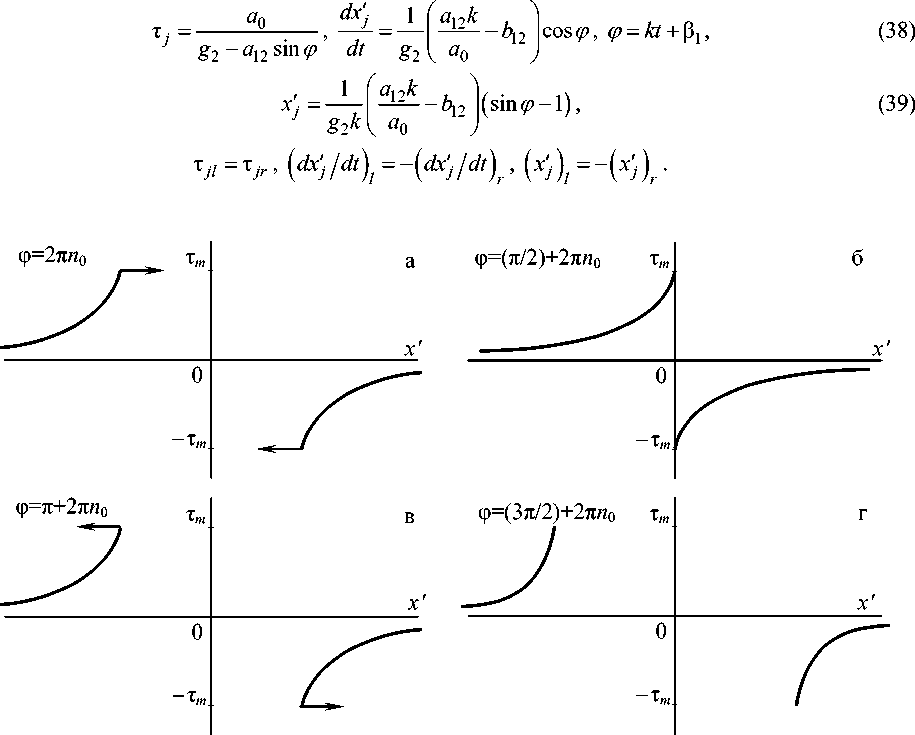
Рис. 3. Колебания двух монотонных ветвей, имеющих одинаковые знаки наклона. Стрелка указывает направление движения

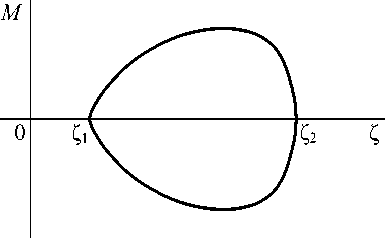
Рис. 4. Петля динамического гистерезиса на плоскости «наклон ветви – скорость τ m - изолинии»

Здесь следует принять g 2 = 2 a 12 A j , A j >1. Условие а 2 >  а 2 т 2 означает, что

( т 2 )     = S j ( - Q i ) ( д ² - 1)/ Q 3 , ф 1 =(п/2)+2п n о , S j e ( 0,1 )

и приводит к связи 5j2 = 1/ (2Ау -1) . В качественном отношении процесс колебаний этих ветвей похож на случай (33), (34) (рис. 2), но теперь на границах ветвей имеем периодическую зависимость τj от времени, см. (38). При φ = φ1 две смыкающиеся ветви образуют слабый разрыв. Для

Ф = 2 пп 0 трансзвуковой переход существует при высоких частотах, если р ² > A j >  1.

При рассмотрении ветвей, имеющих одинаковый знак наклона, поступаем следующим обра зом. Левая ветвь: дт/дx'> 0, т е(0,тjl^, x'е(—да,xj^,  a0 >0, a12 >0, b12 < 0, g2 > 0. Правая ветвь: дт/дx' > 0, т е _тjr ,0), x'е [xjr, да), a0 < 0, a12 > 0, b12 > 0, g2 > 0 . Здесь справедливы формулы (38), (39), в которых выбор знаков коэффициентов соответствует наименованию ветви:

—

^т j = ^т jl =

тjr, (dxj/dt) = (dxj/dt) = —(dxj/dt) , xj = xj = — xjr. При ф = (п/2) + 2nn0 эти ветви lr образуют неподвижный сильный разрыв. Рассуждения, относящиеся к выбору параметров g2, Aj, 52 и условию появления трансзвукового перехода, остаются такими же, как и в предыдущем случае для ветвей с наклонами разных знаков. Качественная картина колебаний аналогична той, что показана на рис. 3, но теперь граничная функция тj содержит синусную зависимость от времени, см. (38).

Колебания слабого и сильного разрывов. Вернемся к интервалу низких частот и обсудим физическую модель решения при Ь1 = 0: см. соотношения, сопутствующие формуле (28). На интервале т е(0,Tm ] две монотонные ветви смыкаются друг с другом при т = Tm=const и образуют слабый разрыв. Левая ветвь: дт/дx* > 0, x е(—да,x^], a0 > 0, a1 > 0, a2 >0, a12 >0, b0 < 0, b2 < 0 . Правая ветвь: дт/дx*< 0, x' е[x'm,да), a0 < 0, a1 < 0, a2 < 0, a12 < 0, b0 > 0, b2 > 0. Расположение ветвей похоже на то, что изображено на рис. 2, б. Обе ветви примыкают друг к другу при всех t> 0. Скорость слабого разрыва равна dxm/dt = —(b0 + b2тт cos kt)/[a0 + a12Tm sin(kt + P1)] • (40) В этой формуле выбор знаков коэффициентов соответствует наименованию ветви: ( dx’mldt)l =(dx'mldt)r •

Другой вариант построения ветвей выполняется следующим образом. Левая ветвь: т e (0, T _m ] , дт/ д x' >  0, x ' е ( —да , x’_m ] , a ₀ >  0, a 1 > 0, a ₂ > 0, b ₀ <  0, b ₂ <  0 . Правая ветвь: т е [ — т _m ,0 ) , д т/ дx' >  0, x е [ x_m , да ) , a ₀ <  0, a 1 >  0, a ₂ >  0, b ₀ >  0, b ₂ <  0 . Схема расположения ветвей аналогична той, что показана на рис. 3, б . Эти ветви примыкают слева и справа к линии x’ m = x m ( t ) , t > 0. Такая конфигурация ассоциируется с сильным разрывом, на котором функция

т(x', t) меняется скачком от -тт до тт. Скорость разрыва равна dx m =__( b0 )l,r + ( b2 ) 1,r (±Tm ) cos kt____________

^dt      ( a 0 ) _l , r ⁺ ( ^a 1 ) l , r ( ^{± T} m ) ^sin kt ⁺ ( a 2 ) l , r ( ^{± T} m ) ^cos kt ’

( dx'mldt ) l = ( dx'mldt ) r •

Для вариантов (40) и (41) линии динамического гистерезиса на плоскости (Z, Z) имеют вид, аналогичный (36):

Z = ± a\ F ( Z ) _ a 2

।   ; Z = 1 + a ⁰ M .

Функция F (Z) определяется формулой (37).

Заключение. Волновое уравнение (1) с источником (7) имеет точное частное решение (4), (5). Основные свойства решения детерминированы выбором знаков коэффициентов Q i , Q ₃ и характером зависимости коэффициента а ₃ от частоты возбуждающих колебаний источника (см. (21), (26)-(30)). Рассмотрены колебания высокой и низкой частоты. Изучены свойства т, -изолиний: кинк-пульсации; знакопеременность скорости изолиний; дозвуковой и сверхзвуковой режимы движения; трансзвуковой переход. Представлены три группы задач, связанных с физической интерпретацией решения: задача с неизвестной подвижной границей (31); колебания двух монотонных ветвей, периодически сближающихся и удаляющихся друг от друга; конфигурация волнового типа - слабый либо сильный разрыв, движущийся вдоль координатной оси.