Волновые структуры в комплексных сплошных средах, включая атмосферу, гидросферу и космическую плазму

Рассматривая классы нелинейных GKP- и DNLS-моделей, в качестве исходной будем и спользовать систему уравнений гидродинамики с граничными условиями [1]:

д t v + ( v v ) v + ( c ² / p ) Vp = 0, д t p +v ( p v ) = 0;

д₍Ф + ¹ (VФ) 2 + c ^{(p-p 0} ) + Lz = 0, АФ = 0;

t 2(     )         2 p p ,’ д^п + дуП дуФ +5vn д.,Ф-д„Ф = 0, t xx yy z дt ф + 1 (VФ)2 + (c2 / p) n = 0;

z = n( x, y, t), д2Ф z =-pQ

волны в замагниченной плазме. Первые два уравнения - уравнения движения и непрерывности для обобщенных скорости и плотности соответственно. Для волн на «мелкой» воде v – скорость частиц («массовая» скорость), для ионно-звуковых волн – скорость ионного «звука», для МЗ-волн v = h = H ~ / H _o - безразмерное магнитное поле ( H ~ - поле волны). Следующие два уравнения -уравнения для потенциала ( v = grad Ф ), последние четыре соотношения – граничные условия. Изучая обобщенные уравнения, мы осуществляем общий подход, отвлекаясь от конкретного вида среды. Используя разложение по степеням малых параметров, как это сделано в [1; 2], можно получить уравнение:

д tu + а и д xu + вд 3и = ^ , (2) в котором, например, для волн на поверхности жидкости

а = 3 c о /2 H ,    c о = ( gH ) 1/²;

^ = - ( c ₀ /2) V_i w ,    d xw = V_i u ;

p = c o I 3 2- H ²

6 Ipg если H ^ (3g / pg)1/2, в ^[и] появляется высшая дисперсионная поправка -Чд5и, где Y = (cо/6)х X [H2(5H2 - 2 / pg) - 12(3g / pg - H2)2].

Для БМЗ-волн в замагниченной плазме дисперсионный коэффициент имеет вид p = V a ( c ² / 2 to' 0 i ) (cot 9 - me / mi ), и когда угол между вектором k и полем B 9^ arctan( mi / me ) ¹^² , функционал ^ [ и ] в (2) должен быть дополнен дисперсионным членом -Y^ Xu , с коэффициентом дисперсии

Y = v_A ( c 4 /8 to 4 i ) х

х

3 ( me / mi - cot ² 9 ) - 4cot 4 9 ( 1 + cot ² 9 )

При учете диссипативных эффектов в среде в правой части (2) появляется член ^ [и] = vd2u, где, например, для ионно-звуковых волн в плазме v =

2    2    ”.

= (p0 / 2p)(c2 - c2) т   5ф(5)d5 имеет смысл коэф- фициента релаксационного затухания «звуковых» колебаний; функция ф(t, т) определяет релакса- ционный процесс. С учетом всех рассмотренных эффектов можно записать обобщенное уравнение (Belashov – Karpman (BK) equation):

д tu + A ( t , u ) u = f ,

x f = k|

-a

A_± udx ,

Ai =ay+a2, где при A(t, u) = audx - д2 (v - рдx - уд3) будем иметь обобщенные уравнения класса GKP, а при A(t, u) = = 3s | p |2 u2дx -д2(iX + v) - уравнения класса DNLS, где и = h = (By + iBz )/2 B 0|1 -p |1/2; h = Bi / B0; p = = (1 + ie):

d th + s d _x I I

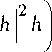
- iXd2h -vd2h = g [

-”

A i hdx .

Обе модели не являются в математическом смысле полностью интегрируемыми, аналитически мы можем только выполнить анализ устойчивости решений на основе метода исследования трансформационных свойств гамильтониана системы [2] и качественный и асимптотический анализ решений: построить классификацию решений в многомерном фазовом пространстве и по характеру асимптотик [4].

Для исследования устойчивости решений запишем уравнение GKP в гамильтоновском виде: д _tu = д _x ( 5 H / 5 и ) с гамильтонианом

H = J [- ( s /2)( д xu ) ² + ( X /2)( д 2 и ) ² +

+ (Viдxv)2/2 -u31 dr, имеющим смысл энергии системы. Рассмотрим

¹ J u ² d r .

вариационную задачу: 5 ( H + u Px ) = 0, Px =

Такая запись означает, что все финитные решения есть стационарные точки гамильтониана Н при фиксированной проекции импульса Px. Задача устойчивости состоит в том, что, в соответствии с теоремой Ляпунова, в динамической системе точ- ки, которые отвечают минимуму или максимуму Н, являются абсолютно устойчивыми. Рассмотрим деформации Н, сохраняющие проекцию импульса Px: и (x, т!) ^С1^2^11 d )/2 и (x / Z, ri / п). Гамильтониан уравнения GKP как функция деформационных переменных приобретает вид гг/. \     .-2 1 .2 -2    .-1/2 (l-d)/-2 .-4

H (Z, п) = a Z + b Zn - c Z    П( ) + eZ , где коэффициенты a = --| J (dxu )2 dr, b = 1J (Vid xV )2 d Г, c = J u 3 dr, e = ~J (d2u)2 dr.

Необходимое условие экстремума: ^ H = 0, d n H = 0.

Достаточное условие минимума гамильтониана:

d Z h ( Z , n ) d² n h ( Z , n ) s Jz H ( Z , n ) д П H ( Z , n )

> 0,

д² H ( Z , n ) >  0.

Совместное решение этих уравнений и неравенств позволяет доказать возможность существования в GKP-модели абсолютно и локально устойчивых решений, условия устойчивости 2D- и 3D-солитонных решений представлены в [2].

Для исследования устойчивости решений уравнения 3-DNLS оно также записывается в виде [3; 4]: д _th = д x ( 5 H / 5 h ) с гамильтонианом

H =

J ■1|h| +Xshh дxф +1 G(Viдxw)2 dr, д2 w = h, ф = arg( h).

Вариационная задача формулируется следующим образом: 5 ( H + u Px ) = 0, Px = ¹ J | h | ² d r . Решая задачу устойчивости, рассмотрим деформации H , сохраняющие проекцию импульса Px : и ( x , z i ) ^

а )                                                                                           б )

Рис. 1. Общий вид 2D-решений уравнения GKP: у = 1, р = - 0,8 ( t = 0,2) ( a ); у = 1, р = 3,16 ( t = 0,5) ( 6)

а )                                                                                           б )

Рис. 2. Формирование 2D-бисолитона при и 1 (0) = 1,35, и ₂ ( 0 ) = 1,3, kx (0) = 6: t = 0,2; t = 1,2

^Z 1/2П 1 h(x/Z, ri/n),   Z,neC Гамильтониан уравнения 3-DNLS приобретает вид

H (Z, H) = a z 1H 2 + b Z-1 - c Z2H 2, где a = 1 fl h |4 dr, b = X sf hh * dx ф dr, c = ^ f (Vid xw )2 dr.

Анализ ограниченности гамильтониана Н выполнялся аналогично случаю уравнения GKP. В итоге мы доказали возможность существования в модели 3-DNLS абсолютно и локально устойчивых 3D-решений и получили условия их устойчивости (т. е. области значений коэффициентов уравнения 3-DNLS) [4].

Асимптотики решений уравнений GKP-класса были подробно исследованы в работе [5] для функции w = u ( Z , H , t )/ V . При этом было получено

• - для случаев V >  0, у = - 1 и V <  0, у = - 1:

  w = A1 exp <  (2 у ) ^1/2

  
  

■           /-------------Л 1/2

C ² + C4 ⁴ ± 4 y x^ ,

• т. е. решения экспоненциально затухают на ±» ; - для V <  0, у = 1:

w = A2 exp{ (2C-1у-1/2)-1(2C-2у1/2 -1)1/2%} х хcos{ (2С-1у-1/2)-1(2С-2у1/2 + 1)x + ®}, где A1, A2 и @ - произвольные постоянные;

N =| ^V|

1/4

, x = [n±Z + (к-V)t], т. е. асимптотики являются затухающими осцилляторными.

Таким образом, было установлено, что в зависимости от знаков V и Р уравнение GKP может иметь 2D-солитонные решения с монотонными и осциллирующими асимптотиками (рис. 1).

При исследовании взаимодействия 2D-солито-нов уравнения GKP использовались специально развитые методы численного интегрирования, основанные на конечно-разностных и спектральных подходах [1; 2]. При этом, в частности, было установлено, что могут наблюдаться как тривиальные, аналогичные 2D-солитонам уравнения КП, случаи взаимодействия, так и совершенно нетривиальный (и невозможный в «классической» модели КП) случай формирования устойчивых солитонных пар (связанных состояний) – так называемых bi-солитонов [1; 2] (рис. 2). Диссипация в системе непосредственно влияет на структуру 2D-сол и тонов. При этом наблюдается эффект удлинения солитонного «хвоста», а также уменьшение частоты осцилляций и гашение колебаний позади главного максимума.

В работах [2–5] нами были исследованы многочисленные приложения модели уравнений класса GKP в физике реальных сред с дисперсией, в частности: динамика ионно-звуковых и быстрых магнитозвуковых волн в плазме (ионосфера и магнитосфера Земли, астрофизика); динамика солитонов на поверхности «мелкой» жидкости (гравитационные и гравитационно-капиллярные волны, цунами); возмущения в атмосфере и ионосфере, генерируемые импульсными источниками (сейсмические процессы, солнечное затмение и терминатор, мощные искусственные взрывы); эволюция в средах с переменной дисперсией (волны в жидкости, волны в плазме). Сравнение полученных при этом результатов с известными экспериментальными данными говорит об адекватности модели GKP для описания нелинейных волновых процессов в реальных физических средах с дисперсией.

Для исследования динамики вихревых структур в качестве исходных рассматриваются уравнения Эйлера, от которых для исследования вихревого

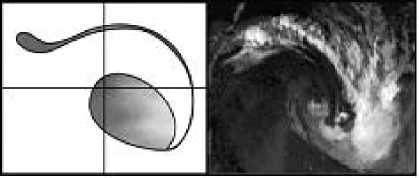
Рис. 3. Моделирование эволюции синоптических вихрей циклонического типа (слева – численный эксперимент, справа – спутниковая фотография)

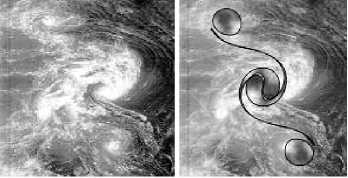
Рис. 4. Моделирование 4-вихревого взаимодействия в канале Naruto (Япония) (справа - численный эксперимент, слева - аэрофотосъемка)

движения мы переходим к уравнению переноса для плотности р и уравнению Пуассона для функции тока ψ [6]:

∂ _t ρ+ ( v ∇ ) ρ=ν∇ ² ρ , ∆ψ- f =-ρ , v = B ^{- 1} [ ∇ , ψ e _z ], e _z = e _x × e _y .

Здесь v - кинематическая вязкость. Эти уравнения описывают сплошную среду или квазичастицы (заряженные нити, вытянутые вдоль однородного поля B ) с кулоновским взаимодействием [6]. Смысл переменных зависит от типа среды. Для моделирования нами использовался модифицированный метод КД, развитый в [7; 8].

На рис. 3 и 4 показаны примеры моделирования таких систем, как синоптический вихрь (в сравнении с реальной циклонической системой) и вихревые образования в жидкости, когда результатом взаимодействия является образование ком- плексной структуры с межвихревыми пеленами, соединяющими вихри системы.

Таким образом, используя полученные в работах [6-8] результаты, мы можем эффективно моделировать (а следовательно, и прогнозировать) эволюцию реальных вихревых систем.

В работах [6; 8–10] представлены результаты для ряда других вихревых систем: эволюция торнадо с поперечными возмущениями его оси; взаимодействие потоков заряженных частиц в плазме магнитосферы и ионосферы, формирование завихренностей и вихревых цепочек при обтекании тел потоками газа и жидкости; образование и эволюция вихревых структур в астрофизике (спиральная структура галактик, солнечная вспышечная активность – магнитные петли и трубки в солнечной короне); проблема магнитного удержания и УТС; вихревые движения в плазме, относящиеся к плазменным технологиям.