Волновые уравнения электромагнитных волн в ограниченных областях с ферритовым заполнением с ортогональной формой поперечного сечения при продольном намагничивании

Многочисленные приборы, использующие ферриты, выполняют функции невзаимных (вентили, циркуляторы) или быстро управляемых (модуляторы, переключатели, фазовращатели) устройств [1].

Анализ распространения электромагнитных волн (ЭМВ) в регулярных гиротропных (ферритовых) ограниченных областях, на основе которых функционируют ферритовые приборы, достаточно хорошо проведен для случаев с круглой и прямоугольной формами поперечного сечения при продольном намагничивании [см. например 1, 2, 3, 4]. Однако в настоящее время недостаточно полно исследовано распространение ЭМВ в гиротропных эллиптических ограниченных областях.

Общая природа распространения ЭМВ в гиротропных ограниченных областях позволяет разработать единую теоретическую модель. Математической основой данного анализа является тензорное исчисление, описывающее инвариантность уравнений ЭМП для различных систем координат.

Задачей данной статьи является получение общих выражений, описывающих распространение ЭМВ в гиротропных произвольно намагниченных ограниченных областях с ортогональной формой поперечного сечения, и вывод на их основе волновых уравнений гибридных волн для эллиптических, круглых, прямоугольных областей при продольном намагничивании.

Волновые уравнения НЕ-волн

При рассмотрении процессов, гармонических во времени (зависимость от времени примем в виде e jwt ), уравнения Максвелла без наведенных токов и зарядов имеют вид [3]:

rotH = jw s E ; rotE = - jwB ;

divE = 0; divB = 0, где E, H - соответственно напряженности электрического и магнитного полей; s - абсолютная диэлектрическая проницаемость среды; sE = D - электрическая индукция; B - магнитная индукции; j – мнимая единица; w – циклическая частота.

При распространении волны в магнитогиротропной среде магнитная индукция B в системе (1) примет следующий вид:

B = || p| H ,                                               (2)

		p 11	jk	jl
где	II p ll=	- jk	p 22	jm
		_- j	- jm	p 33

тензор магнитной проницаемости феррита,

p ₁ 1 , p ₂₂ , p ₃₃;k , l , m - компоненты тензора; j - мнимая единица.

В случае же распространения волны в изотропной среде тензор магнитной проницаемости в выражении (2), как и диэлектрическая проницаемость, станет скалярной величиной. Разложив rotH , rotE системы (1) по координатным осям, получим:

V 2 H 3 + j y H 2 = jw ^{s E} , ,

1 5 h

1– h 1 d q 21

^V , ^H 3 + j y H , = ^- jw ^{s E} 2 ,

• 5 ,    H ₂ - 5 ₂ H ₁ = jw s E ₃ .

'v 2 E 3 + j y E 2 = - jw ( p„ H , + jkH 2 + jlH 3 ),

■ V , E 3 + j y E , = jw ( - jkH , + p 22 H 2 + jmH 3 ),

.5, E2 - 52 E, = - jw (- jlH , - jmH 2 + p 33 H 3 ), где v,

• ^{1    d 1} s? ^{1 f d} г 2 ^s — ^{1 f d} 1 г' 1      ²      1 d hi и г¹

I , 5 1 = I + Г 21 I , 5 2 = I + Г 12 I , Г 2, = ^и Г 12

h ^d qj       h 1 (5 q 1        J         h 2 ( ^d q 2        J h 2 ^d q 1

символы Кристоффеля; h – коэффициенты Ламэ; q ₁ , q ₂ – обобщенные поперечные координаты.

Распишем d vB :

divB = 5 B ₁ + 5 ₂ B ₂ - j y B ₃ = 5 _t ( p„ H ₁ + jkH ₂ + jlH ₃ ) +

+ 5 2 ⁽- jkH 1 + p 22 H 2 + jmH 3 ) - j y ⁽- jlH 1 - jmH 2 + p 33 H 3 ) = 0.

После компоновки, выражение (5) примет вид:

divB = jk ( 5 ₁ H ₂ - 5 ₂ H ₁ ) + 5 _X ( p_n H ₁ + jlH ₃ ) +

+ 5 2 ( p 22 ^H 2 + jmH 3 ) - j Y ( - jlH 1 - jmH 2 + P 33 H 3 ) = 0.

В выражение (6) подст а вим третье уравнение системы (3):

div B = 5 j ( p _xx H j + jlH ₃ ) + 5 ₂ ( p 22 H ₂ + jmH ₃ ) - w s kE ₃ -

• ^- j Y ^{( -} jl ^H 1 ^- jm ^H 2 ⁺ p 33 ^H 3 ) = ⁰

или

⁵ 1 ⁽ p u ^H 1 ^{+ jlH} 3 ^{)+ 5} 2 ⁽ p 22 ^H 2 ^{+ jmH} 3 ) = = w s kE ₃ + j y ( - jlH _t - jmH ₂ + p ₃₃ H ₃ )

Выразим составляющие E ₁ и E ₂ из формулы (3) и подставим в первые два уравнения си-

стемы (4):

V 2 E 3 + j y I . V 1 H 3        H 1 I      jw ( p 11 H 1 + jkH 2 + jlH 3 )>             zm ( jw s           w s J                                              (9) v 1 E 3 + j y | . v 2 H 3 + y H 2 |= jw ( jk H 1 + p 22 H 2 + jm H 3 )- ( jw s           w s J

На первое уравнение системы (9) воздействуем оператором 5 ₁ , а на второе уравнение (9) -оператором 5 2 :

A 12 E 3

—

^Y A 11 H ₃ — j ^— 8 1 H 1 +

w е          w е

+ jw 8 1 ( ц 11 H 1 + jkH 2 + jlH з ) = 0,

A 12 E 3 + --- A 22 H 3 + —--- 8 2 H 2 w е w е

—

— jw 8 2 ( — jkH 1 + ц 22 H 2 + jmH 3 ) = 0.

В (10) учитывалось, что дифференциальные операторы второго порядка имеют вид:

<

8 2 V 1

8 2 V 2

8 1 V 1

8 1 V 2

1 [	— + Г 2 1 . d q 1         21 J	f 1	d	I 1	d	d
h 1		( h 2	d q 2,	h 1 h	2 d q	1 d q 2
- 11	f d + Г 1 ' <5 q 2       12 у	I f 1	d '	1 - 1	d	d
h 2		1 ( h 1	d q 1 ,	h 1 h	2 d q	2 d q 1
-1 f	7^+ Г 221 ^1 d q 1          JI	f 1	d |	-1 f	d	+ Г 221
h 1 (		< h 1	a q 1 J	h 1 2 (	a q 1
1 = h f	f— + г 112 (a q 2	— Г	2 ) 21 =	A 22 .

—

^A 12 ,

^A 21 = ^A 12 ,

Г 112 I = ^A 11 ,

От первого уравнения системы (10) вычтем второе:

( a 11 H ₃ + A ₂₂ H ₃ ) + j — ( 8 1 H 1 + 8 ₂ H ₂ ) + wk ( 8 1 H ₂ — jw [ 8 1 ( ц„ H 1 + jlH 3 ) + 8 2 ( ц 22 H 2 + jmH 3 ) ] = 0.

^{— 8} 2 ^H 1 ^{) —}

Подставляем в (12) третье уравнение системы (3) и (8):

A 11 H ₃ + A ₂₂ H ₃ + j y ( 8 1 H 1 + 8 ₂ H ₂ ) — jw ² - IH 1 — jw ² е mH ₂ +

+ w ² ец ₃₃ H ₃ = 0.

Формула (13) позволяет получить волновое уравнение НЕ-волны в гиротропной области с ортогональной формой поперечного сечения при различных случаях намагничивания.

При продольном намагничивании тензор магнитной проницаемости феррита имеет вид [3]:

где

ww ц = ц 0 + ц 0 2 0 M 2;

w 0 — w

—

k = Ц о

—

ц	jk	0
jk	ц	0
0	0	ц || _

, wM ww M

2         2 ;

w ₀ — w

= ц0YM 0; Y = 1.76 ■ 1011 Кл кг

–

гиромагнитное

отношения для спина электрона; w ₀ = ц ₀ YH ₀ - частота ферромагнитного резонанса; ц ₀ - магнитная постоянная; М ₀ – намагниченность феррита; Н ₀ – намагничивающее внешнее магнитное поле.

Знаки перед недиагональными компонентами в (14) могут быть противоположными, если взять k =

—

ц 0

ww M

w

Уравнение

—

.

w ₀ ²

при

( k * 0, l = m = 0, ц 11 = ц ₂₂ = ц , ц 33

продольном

= ц ) ^:

намагничивании

примет

вид

A., H ₃ + A,H. + j y ( 8.H. + 8,H, ) + w ² ец,,H₃ = 0. 11     3          22     3                1     1         2     2                   ||     3

А divB при продольном намагничивании согласно (7) примет вид: divB = 8 1 ц H 1 + 8 ₂ ц H ₂ — w е kE ₃ — J y^ H ₃ = 0 .

Преобразуем (16):

w s kE, + /уц,, H,

8 1 H 1 + 8 ₂ H ₂ =------³—     ^{11 3}

.

Ц

Подставив (17) в (15), получим волновое уравнение гибридной НЕ-волны в гиротропной продольно-намагниченной регулярной ограниченной области с ортогональной формой поперечного сечения:

A.. H₇ + A₂₂ H₇ + 1 w ² ец.. - —у ² | H₇ + jywe —E₇ — 0.             ⁽¹⁸⁾

11 Z        22 Z                ||                      Z                      Z

( ц j ц

В (18) учитывалось, что волна движется вдоль оси Z (Н3 = HZ) и внешнее намагничивающее магнитное поле тоже направлено вдоль оси Z . В выражении (18) знак перед EZ может быть противоположным, если взять k_ — - ww M .

^ц 0      w ^{2 -} w 2

Используя (18), получим волновые уравнения для конкретных конфигураций ограниченных областей.

Определяя коэффициенты Ламэ согласно [5], а символы Кристоффеля – [6], получим из (11) дифференциальные операторы второго порядка для разных областей:

• а)    прямоугольная область ( x, y, z ) :

л - 5 2 л - 5 2 -

( 0)

( 1)

A —     , A —

• ¹¹ д x ^{2      22} д у ²

• б)    цилиндрическая область ( r, ф, z ) :

_Л 1 д ²      1 д .         1 д ² .

A 11               +        , A 22

r ² д r ² r д r          r ² д ф

• в)    эллиптическая область ( ^,ф,z ) :

л -   1    5 2 л -   1

A11 =   2 7 2 а е 2 ’ A 22 =   2 7 2 а 2 ’ e d д §         e d д ф где e - фокусное расстояние; d2 — ch§- - cos2 ф.

Подставив (19)-( 1) в (18), получим волновые уравнения гибридных НЕ-волн в гиротропных регулярных продольно-намагниченных ограниченных областях соответственно с прямоугольной, круглой, эллиптической формами поперечного сечения:

д ² H_z д ² H_z    ( ₂        Ц\\ Д _и ■ k ,

2Z +    2Z +|w ецY |HZ + JYws —EZ — °;

д x      ду    ( ц J ц д2hz   1 дhz    1 д2hz ( 2 ц\\ Л . k „

Z+-Z +        / +| w ец\\_ Y | HZ + jyw s —Ez — 0;

д r r д r r д ф     ( ц j ц д Н7 д Н7      2-12 ( 2        ц\\ 2 1тг - 2 7 2 k аГЭА^

---Z +Z + edI w^ец.-у |Н7 + jedvws —Е7 — 0.        (24) ||ZZ д §     д ф ( ц j ц

Уравнение (22) совпадает с уравнением, полученным в [3, 7], а (23) – с [7], что подтверждает правильность полученных результатов.

Волновые уравнения ЕН-волн

Для получения волновых уравнений гибридных ЕН-волн из первых двух уравнений системы

(4) путем взаимных подстановок выразим поперечные компоненты магнитного поля:

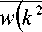
Н 1 —

Е 2  „-----V1Е 3 + w (k _ ц11 ц 22 )

J Y k

^{— ц} 11 ^ц 22

E 1

--j^ 22---- V Е. + — w ( — 2 - ц 11 ц 22 )          w l k Н 2 — --/—2--------- ^ 2 Е 3 +-- Р" w ( — - цн ц 22 )         w ( k	YЦ 22 Е +_ ( — - цц ц 22 )      к j Y k      Е + 2 - ц 11 ц 22 ) 2	jl ц 22 2           H 3 - ц 11 ц 22
+               1V 1 Е 3 w ( k - ц 11 ц 22 )         w (	YЦ 11     Е +_ к - ц 11 ц 22 )       к	Jm^xx Н - ц 11 ц 22

На формулу (25) воздействуем оператором d ₂ , а на формулу (26) - 5 1. Затем от первого

уравнения вычтем второе и в полученное выражение подставим третье уравнение системы (3): ц . A., Е , + ц ₂ A₂₂ Е , + j y ( ц_и8_ДЕ, + ц,5,Е-, ) + w ( ц, m 5, - ц₂ / д ₂) Н. +

11   11   3        22    22   3              11   1   1        22   2   2              11      1        22    2      3

+ Y —w ( - 1Н 1 - mH ₂ - j ц 33 Н ₃ ) - w ² s ( k ² - ц 11 ц ₂₂ ) е ₃ — 0.

Из уравнений Максвелла (1) при отсутствии зарядов выразим divE , учитывая, что D = ε E : divE = δ ₁ E ₁ + δ ₂ E ₂ - j γ E ₃ = 0,                             (28)

т.е. δ ₁ E ₁ + δ ₂ E ₂ = j γ E ₃ .                                           (29)

Из уравнения (27), учитывая (28) или (29), получим волновое уравнение гибридной ЕH-волны в гиротропной продольно-намагниченной регулярной ограниченной области ( k ≠ 0, l = m = 0, µ ₁₁ = µ ₂₂ = µ , µ ₃₃ = µ _|| ) с ортогональной формой поперечного сечения (волна движется вдоль оси Z):

Δ ₁₁ E_Z + Δ ₂₂ E_Z + ( w ² εµ _⊥ - γ ² ) E_Z - j γ kw µ ^|| H_Z = 0,             (30)

µ

• µ ² - k ²

где µ _⊥ =          .

µ

В выражении (30) знак перед HZ может быть противоположным, если взять k = -µ0

ww

M

^. w ² - w ₀ ²

Подставив (19)-(21) в (30) получим волновые уравнения гибридных ЕН-волн в гиротропных регулярных продольно-намагниченных ограниченных областях соответственно с прямоугольной, круглой, эллиптической формами поперечного сечения:

∂ E2Z + ∂ E2Z + (w2εµ⊥ -γ2)HZ - jγwk µ|| HZ = 0;

∂x2     ∂y2

∂2E    1 ∂E     1 ∂2E

Z + Z + Z + (w2εµ⊥ -γ2)EZ - jγwk || HZ = 0;

∂r2    r ∂r    r2 ∂ϕ2

Z + Z + e2d 2 (w 2εµ -γ 2 )E - je2d 2γwk µ|| H = 0.

∂ ξ ² ∂ ϕ ^{2                       Z} µ ^Z

Уравнение (31) совпадает с уравнением, полученным в [3, 7], а (32) – с [7], что подтверждает правильность полученных результатов, как и случае НЕ-волн, а выражение (33) является оригинальным результатом.

Заключение

Получены волновые уравнения гибридных НЕ- и ЕН-волн в гиротропной продольно-намагниченной регулярной ограниченной области с ортогональной формой поперечного сечения, инвариантные относительно преобразования координат. На основе данных выражений выведены конкретные волновые уравнения для различных форм ограниченных областей (эллиптической, цилиндрической, прямоугольной). Полученные результаты позволяют построить единую теоретическую модель распространения ЭМВ в гиротропной продольно-намагниченной регулярной ограниченной области с ортогональной формой поперечного сечения.