Волновые возмущения и гравитационные неустойчивости в нелокальной ньютоновской теории гравитации

Открытие тёмной материи и тёмной энергии стимулировали исследования, выходящие за. пределы Общей теории относительности и имеющие своей конечной целью построение "повой физики" и "повой геометрии". Одним из подходов к созданию новых теорий является попытка, сделать гравитацию нелокальной. Вариант такой нелокальной теории гравитации был предложен в работах [1-3]. Особенностью предложенного в указанных работах подхода, является то, что нело-калыюсть гравитационного поля проявляется как пространственная дисперсия части барионного вещества, позволяя отождествить последнее с "тёмной материей". Таким образом, в предлагаемом подходе свойства, тёмной материи обусловлены предполагаемой пелокальпостью гравитационного взаимодействия, то есть, в конечном итоге, геометрией пространства-времени. Указанная интерпретация тёмной материи позволяет по-новому взглянуть па. известные астрофизические и космологические задачи [1-3].

В данной работе, в рамках указанного выше подхода, в ньютоновском приближении анализируются особенности распространения плоских волновых возмущений и гравитационная неустойчивость в неподвижных однородных изотропных сплошных средах, состоящих из барионного вещества, темной материи и темной энергии.

1. Возмущения и неустойчивости в гравитирующих сплошных средах с пространственной дисперсией

Учёт предполагаемой пелокальпости гравитационного поля в перелятивистском приближении приводит к появлению в уравнении Пуассона, дополнительного интегрального слагаемого, которое можно интерпретировать как вклад, обусловленный наличием тёмной материи [1-3]. В результате, полная система, уравнений, описывающая движение иерелятивистской сплошной среды, принимает вид:

Г д] + V (рФ) = 0,

Г f + (yV)V = -] VP — Vр,                           (1.1)

I Ар = 4irG(p + pD — рл), где риг- плотность и скорость барионной материи, P = P(р) - давление, р - напряжённость гравитационного поля, а.

P d (r) = j К (г — r ‘' )p(r ^r )dr ‘

(1.2)

есть плотность тёмной материи, которая зависит от плотности барионной материи посредством интеграла по всему объёму, занимаемому этой материей. Благодаря ядру К(т — г ’ ) связь между P d и р является нелокальной, что означает наличие пространственной дисперсии в системе. По сравнению с работой [1] здесь дополнительно учтена, плотность, обусловленная космологической постоянной Л (плотность "тёмной энергии") р л = -plc |4Ф1-

Преобразуем систему (1.1), выделив невозмущенное решение (индекс 0) и соответствующее малое возмущение (индекс 1) в виде: р = р₀ + р 1 , р = р₀ + р 1 = р 1, P = P₀ + P 1, г = ф + Ф = Ф (ро = const^ P ) = const), а на ядро К наложим условие:

j K(r)dr =

Р л ^— Ро

Ро

> 0.

(1.3)

Условие (1.3) позволяет решить известную проблему ненулевой начальной плотности в задаче о гравитационной неустойчивости неподвижной однородной сплошной среды [4]. Отметим, что плотность рл больше чем на 3 порядка превышает среднюю плотность современной Вселенной [4]. С учетом (1.3) после линеаризации система. (1.1) может быть сведена, к одному интегро-дифференциальному уравнению описывающему возмущения плотности pi, распространяющиеся вдоль оси ж:

^р- = "2 "ly ^{+ 4?Г}Ро ^G [pi ⁺ /    ^К (ж - ж’) Р1 (ж‘^’'"'j ,

(1-4)

где u_s - скорость звука.

Вид ядра К уравнения (1.4) достаточно сложен, однако его можно аппроксимировать функцией, которая качественно сохраняет основные свойства ядра, но позволяет упростить уравнение. В общем случае ядро К (ж) обладает следующими свойствами: 1) в силу пространственной однородности среды зависит только от разности координат: К (ж — ж’); 2) в силу изотропии среды является чётной функцией К (—ж) = К (ж); 3) спадает на бесконечности К (±^) = 0; 4) нормировано на единицу f + ^ К(ж)с1ж = 1. Всем перечисленным выше условиям удовлетворяет функция [6]:

К (ж — ж’) = —аб (ж — ж’) + (1 + а)70 (ж — ж’),

(1-5)

где 70(ж) = 2 ежр(—q |ж|) - является собственной функцией оператора

(£ — «2}

q - волновое число,

определяющее характерный размер пространственной дисперсии, а - параметр, характеризующий

величину нелокальности.

Подставляя функцию К (ж — ж ) (1.5) в уравнение (1.4) и действуя на получившееся уравнение

оператором

(6 — q 2)

находим:

(Д) — q2А = ”214Р1 — q 2"2 У + 4qpo С(1 — а дгР1 — 8» Gq2 pi.    и дж2 у ot2 / ot2 S дж4       S дж2                  дж2

Выполнив в (1.6) преобразование Фурье, получим закон дисперсии, который удобно записать в

безразмерном виде:

Q2 = к2

-

(1 — а)к? + 2^² к? + ( ²

(1.7)

где П = ^ - безразмерная частота, к = ^ - безразмерное волновое число, ( = -^ - безразмер ный параметр, характеризующий относительный размер пространственной дисперсии, a kj и wj

- волновое число и частота Джинса: k_j =

45? и Wj = v_s kj = V4^Gv ^u s

S •

На Рис.1 приведен типичный график зависимости Q2(к2).

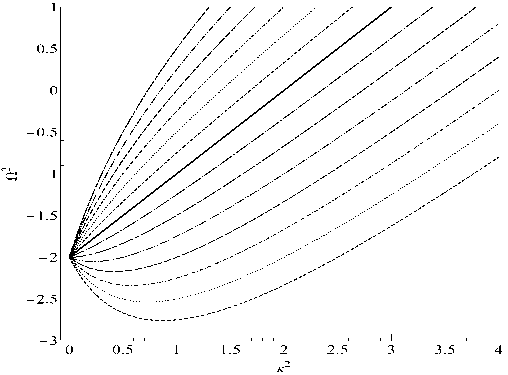
Рис. 1. Зависимость Q² (к? ) при ( ² = 1. Случай Джинса [4] - сплошная прямая линия на графике, соответствует значению о = — 1. Выше лежат кривые, отвечающие значениям о > — 1, а ниже - кривые, отвечающие значениям о < — 1. При о < — (1 + ^²) у изображенных на графике кривых появляются минимумы.

Функция (1.7) обращается в 0 в то^гках к0 = 2 [^(С2 + а — 1)2 + 8^2 — (С2 + а — 1)], которые существуют при любых значениях а и С- При к2 < к0 значения П2 отрицательны: П2 < 0, что соответ ствует гравитационной неустойчивости - возмущение плотности р1 при таких значениях волнового вектора нарастает. Наоборот, при к2 > к0 зиачеиия П2 положительиы: П2 > 0, что отвечает случаю распространения звуковых воли в системе. Кроме того, функция (1.7) имеет минимум в точке K„in = -С2 + -(а + 1)С, который, с учётом требования K„in > 0, реализуется при а < —(1 + С2). Значение функции П2 (к2) в минимуме равно П2 (к^^п) = — ^С + V—(а + 1)) - 2. Величина |П2 (к^„) | возрастает с увеличением С и уменьшением а. Максималыюе значение П2 (к^п) достигается при С = 0 и а = — 1 и совпадает со значением функции П2 (к2) в iгуле П2(0) = —2. Минимумам дисперсионных кривых отвечают характерные времена ттах = ,  1 ^=, которые

V K^iLJ1

определяют наиболее медленное нарастание плотности, обусловленное гравитационной неустойчи востью.

Заключение

Основные выводы данной работы состоят в следующем. 1. Одновременный учёт пространственной дисперсии, обусловленной предполагаемой пелокальпостью гравитационного поля (тёмной материи) и тёмной энергии, обусловленной учетом космологической постоянной, в нерелятивистском пределе позволяет при определённых условиях сделать корректной математическую постановку задачи о гравитациоппой неустойчивости неподвижной однородной сплошной среды. 2. Интегро-дифференциальное уравнение, описывающее плоские линейные возмущения плотности в рассматриваемой системе, может быть сведено к дифференциальному уравнению четвертого порядка. путём моделирования ядра, интегрального члена. Последнее позволяет получить закон дисперсии указанных возмущений в явном виде. 3. Исследование закона, дисперсии рассматриваемых возмущений показывает, что в рассматриваемых системах па. временах, отвечающих минимуму дисперсионных кривых, нарастание плотности в результате гравитациоппой неустойчивости развивается наиболее медленно.