Волны Лэмба в ферромагнитных металлах: лазерная генерация и электромагнитная регистрация

Неразрушающий контроль качества композитных материалов и листовых металлоизделий, широко используемых в авиа- и ракетостроении, основан, как правило, на применении акустических методов контроля. В силу высоких технологических требований указанные методы должны быть преимущественно бесконтактными. По этой причине внимание специалистов привлекают генерация ультразвука в изделии за счет оптико-акустического преобразования (термоупругий эффект) с использованием импульсного лазерного излучения и регистрации ультразвука на основе обратного электромагнитно-акустического (ЭМА) преобразования с помощью широкополосных (по спектру) ЭМА-приёмников.

Так как длительность лазерного импульса на два-три порядка короче импульса, излучаемого пъезопреобразователями, то применение импульсных лазеров в ультразвуковой дефектоскопии значительно сокращает величину «мертвой» (неконтролируемой) зоны ответственного металлоизделия. Кроме того, короткий лазерный импульс генерирует в металлоизделии акустический сигнал широкого спектра, что увеличивает возможности спектрального акустического метода контроля, позволяющего распознавать образы (формы и размеры) дефектов. В свою очередь, регистрация отражённых от дефектов, или испытавших дифракцию на дефектах акустических импульсов с помощью широкополосного ЭМА-приёмника позволяет зафиксировать почти почти все спектральные составляющие сигнала.

Впервые возникновение термоупругих волн в упругом полупространстве под действием внезапного нагревания границы было рассмотрено в так называемой «задаче Даниловской» [1]. В дальнейшем результаты подобных исследований были подытожены, например, в работе [2]. В 1989 году было экспериментально обнаружено влияние магнитного фазового перехода на возбуждение ультразвука в ферромагнитных металлах под действием лазерных импульсов [3]. Теория генерации объёмных акустических волн с учетом указанного выше эффекта была опубликована в работе [4]. Здесь впервые был произведен учёт температурной зависимости термического коэффициента линейного расширения (ТКЛР) среды, испытывающего аномалии в районе точки Кюри, а при определении направленностей лазерных излучателей ультразвука – конечность значений скорости распространения тепла и времени релаксации теплового потока. В дальнейшем были сформулированы основы теории лазерной генерации волн Рэлея в ферромагнитных металлах [5], однако к настоящему времени отсутствуют системные теоретические и экспериментальные исследования свойств Лэмба в указанных металлах. Представленная работа имеет цель восполнить этот пробел.

В теоретическом плане настоящая работа посвящена решению несвязанной задачи динамической термоупругости для бесконечной упругой однородной пластины и выделению в поле векторов смещения слагаемых, описывающих волны Лэмба, которые возникают вследствие действий импульса оптического излучения. На первом этапе определяется температурное поле в пластине, которое было определено по методике, изложенной в работе [6]. На втором – поле вектора смещений, дисперсионные кривые и спектры симметричных и антисимметричных мод соответ- ствующих номеров.

Для определения поля вектора смещения и( r , z, t ) рассмотрим уравнение движения упругой среды [7]

d2 u c2Δu+(c2-c2)grad divu=    +(3-4c2c2)c2α gradT.                   (1)

212      _∂ t 2    211 T

Здесь T(r,z,t) – отклонение температуры от равновесного значения; A – коэффициент по- глощения оптической энергии на границе металла; a – коэффициент температурной проводимости среды; λq – теплопроводность среды. Ось z направлена по нормали к поверхности вглубь среды; r – расстояние от оси цилиндрической системы координат, t – время. Границы пластины, занимающей область z ∈ [0, h] , тепло не проводят.

Представим вектор смещения через скалярный Φ и векторный Ψ потенциалы Ламэ u = grad Ф + rot Р .

Тогда уравнение движения упругой среды может быть записано в виде двух дифференциаль- ных уравнений в частных производных:

∂2Φ 1∂Φ ∂2Φ 1∂2Φ ∂r2+r∂r+∂z2c12∂t2

= f ( r , z , t ),

∂2ψ1∂ψ-ψ∂2ψ-1∂2ψ=0

∂ r ² r ∂ r   r ² ∂ z ² c ₂ ² ∂ t ²

где c ₁ , c ₂ – скорости распространения продольных и поперечных волн соответственно; ψ – отличная от нуля компонента векторного потенциала Ψ = {0, ψ , 0} . В правой части уравнения (3)

учтено изменение ТКЛР α _T с температурой

T ( r , z , t ) f ( r , z , t ) = (3 - 4 c ²) ∫ α T ( T 0 + T ) dT , 0

где T ₀ – равновесная температура в среде; c = c ₂ c ₁.

Решение уравнений (3) и (4) получаем с помощью интегрального преобразования Фурье по времени и преобразования Бесселя по пространственной координате, причем уравнение (3) преобразуется по функции J0 , а уравнение (4) по функции J1 , что обусловлено видом левых частей соответствующих уравнений. Получаем

2*

^∂Φ ₂ - β 1 ² Φ ^* = f ^*( λ , z , ω ),

∂ z

∂2ψ

^-в - ftv = 0, ∂z где β12=λ2-ω2c12, β22=λ2-ω2c22.

Решения уравнений (6) и (7) можно записать в виде

Г i z

Ф ( X ,z, ti ) = By +-- Г f ( X , z, a )exp( —e z ) dz ехр( в z ) +

L 1 2A0J z 1

exp( - β ₁ z ),

⁺ B 2^-^ I f ^{( X} , ^z, ti )^exP^{( e} i ^z ) ^dz .     2 ^в 10

Гуревич С.Ю., Голубев Е.В., Петров Ю.В.

Ψ ^* ( λ ,z, ω ) = B ₃exp( - β ₂ z ) + B ₄exp( β ₂ z ) ,

где неизвестные функции B_i ( ω , λ ), определяющие решение нашей задачи, необходимо получить, используя граничные условия, которые заключаются в отсутствии напряжений на гранях пластины.

Приведем окончательные выражения для проекций вектора деформации на границе пластины, соответствующей z = 0

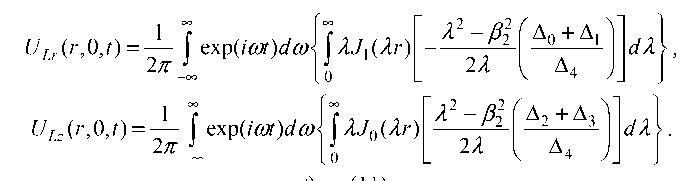
Обратное преобразование Бесселя в (10) и (11) позволяет получить выражение для спектральной плотности импульсов волн Лэмба, возбуждаемых импульсным оптическим излучением в ферромагнитной пластине. Подынтегральные выражения обладают особенностями – полюсами, сумма вычетов в которых и определяет спектральную плотность акустических импульсов, которая, вследствие дисперсии, определяется не только распределением термооптических источников в пластине, но и расстоянием от зоны возбуждения звука. Выражения (10) и (11) также дают и смещения в волнах Рэлея, если перейти к пределу h →+∞ .

Исходными данными являются параметры оптического импульса (длительность, радиус, энергия) и свойства среды: равновесная температура, зависимость ТКЛР, температуропроводность, скорости распространения упругих колебаний, толщина пластины. В заданный момент времени и на заданном расстоянии до точки наблюдения необходимо вычислить значение проекции вектора смещения. Для уменьшения параметров задачи введём безразмерные переменные

η

r

at ₀

, χ

z

t

at ₀

t ₀

константы

η _r

R 0

2 at ₀

at ₀

и параметры интегральных преобразований

κ = λ at ₀ , ξ = ω t ₀

Вычисления были основаны, в основном, на решении задач трех типов. Во-первых, нахождение корня уравнения вида f ( x ) = 0. Во-вторых, нахождение точек экстремума функции f ( x ). В-третьих, вычисление значения интеграла функции. Для каждой подынтегральной функции выбиралась шаговая функция, такая, что погрешность интерполяции не превышала ε = 10 ^{- 8} . При этом результирующая погрешность вычисления избыточной температуры составляет 10 ^{- 7} , а смещений – 10 ^{- 3} - 10 ^{- 4}. Программа была построена таким образом, что зависимость ТКЛР от температуры можно было задавать произвольной функцией (например, полиномиальной).

При расчетах использовались свойства следующих металлов: алюминий, медь, железо и никель, а также железо-никелевого сплава инварного состава 32НКД.

Корни дисперсионных уравнений зависят от частоты, толщины пластины и отношения скоростей объемных волн. Введем безразмерный параметр y = λ h = κχ _r – определяющий волновое число и x = ω hc ₂ = at ₀ ξχ _r c ₂ – параметр, связанный с частотой. Тогда фазовая скорость может быть вычислена по формуле c = c ₂ xy .

На рис. 1 представлены зависимости y(x) для низших мод Лэмба в пластине с параметрами сплава 32НКД. На графиках имеются, но не показаны вертикальные участки, соответствующие малым значениям y , а также участки, где каждому параметру x соответствует два значения y . Нулевые моды A0 и S0 существуют во всем частотном интервале, причём волновое число антисимметричной моды всегда больше yR – волнового числа рэлеевской волны, а симметричной – меньше. Это означает, что при формировании S0 распределение оптико-акустических источников по глубине оказывает большее влияние, чем при формировании Ay. При увеличении параметра x, что соответствует увеличению произведения частоты и толщины пластины, волновые числа стремятся к yR . Это означает, что на верхней грани толстой ( x >> 1) пластины формирует-

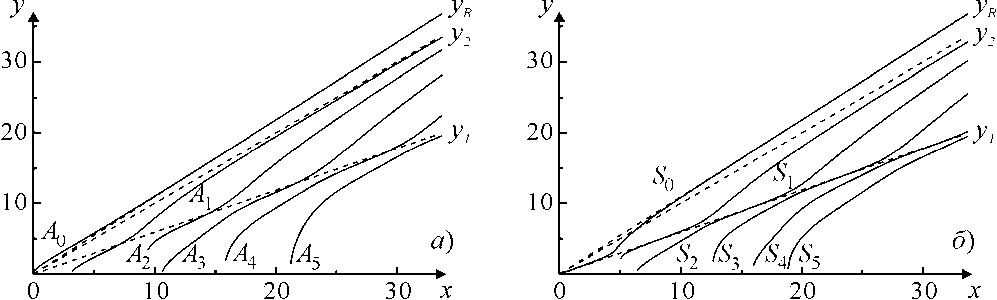
Рис. 1. ^исперсионные кривые ^л^ низших мо^ Лэмба: ( а ) – антисимметричные; ( б ) – симметричные. Сплав 32НК^

ся волна Рэлея, которая является суммой A и S у . Волновые числа остальных мод Лэмба ограничены значением y ₂ ( x ) - волновым числом поперечной волны. Отклонения зависимостей y ( x ) от линейной означают, что разные спектральные компоненты одной моды распространяются с различной скоростью, что приведёт к изменению формы сигнала, соответствующего этой моде, при её распространении.

Далее были определены спектральные функции для нормальных составляющих смещений на поверхности ферромагнитной пластины, в которой распространяются волны Лэмба.

Спектральные функции определяются толщиной пластины, зависят от параметров лазерного импульса и параметров среды, которые могут изменяться с температурой Т у ив процессе поглощения лазерного импульса. Поскольку основным параметром, определяющим амплитуду акустического сигнала при термооптическом возбуждении является ТКЛР и его температурная зависимость, все остальные параметры среды мы будем полагать постоянными.

Расчеты, проведенные для пластин толщиной h = 0,5-5 мм, длительности оптического импульса t у = 15 нс и радиуса пучка R = 1 мм показывают, что при малых h спектр носит выраженный полосатый характер. При увеличении толщины пластины он существенно изменяется и, в результате уширения и наложения отдельных полос, спектр результирующего сигнала становится сплошным. При малых R ₀ спектр результирующего сигнала сплошной и составлен из перекрывающихся полос, а при увеличении радиуса становится полосатым. Энергия лазерного импульса при больших радиусах лазерного пучка преобразуется, в основном, в энергию колебаний низших мод.

Из решения линейной задачи следует, что спектр акустических импульсов пропорционален энергии оптического импульса. Поэтому для выявления изменений, обусловленных нелинейным характером преобразования, будем приводить спектры, отнесенные к максимальной избыточной температуре, которая, в нашем случае, также пропорциональна энергии оптического импульса.

Рассмотрим характеристики акустических импульсов, возбуждаемых в сплаве 32НКД, характеризующимся значительным изменением ТКЛР при нагреве среды от комнатной температуры до температуры плавления и наибольшим ростом в окрестности магнитного фазового перехода.

На рис. 2 показаны модули спектральных плотностей симметричных и антисимметричных мод низших номеров при различной энергии оптического импульса. В скобках показаны величины максимальной избыточной температуры T _max в процессе поглощения оптического импульса. Как показывает расчет, характер зависимости ТКЛР влияет на спектральный состав всех мод, поддерживаемых пластиной. При приближении температуры среды к точке Кюри, которая у рассматриваемого сплава составляет 493 K, наблюдается появление высокочастотной части, также максимум спектра смещается в сторону более высоких частот. Это объясняется тем, что интенсивность оптико-акустических источников изменяется с температурой нелинейно и ее распределение по объему пластины носит более сложный характер.

Гуревич С.Ю., Голубев Е.В., Петров Ю.В.

Наибольшее влияние на спектр акустического сигнала оказывает поведение ТКЛР в окрестности равновесной температуры. Поскольку наиболее существенные особенности ТКЛР соответ-

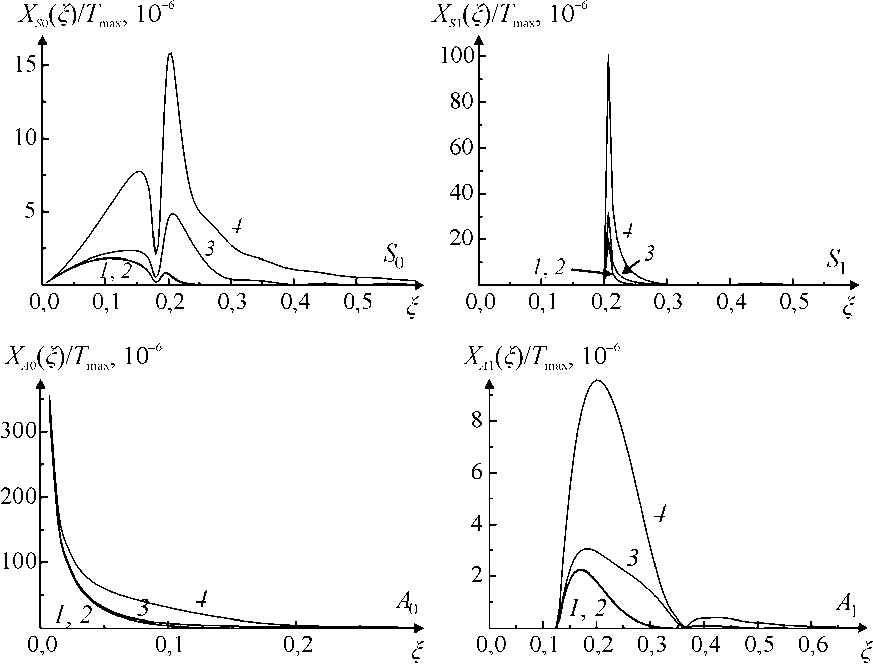
Рис. 2. Спектральные функции нормальных волн. S – симметричные мо^ы. A – антисимметричные мо^ы.

Энергия импульса: 1 - 0,25; 2 - 0,5; 3 - 2,0; 4 - 5,0 мДж. Сплав 32НКД. R0 = 1 мм, h = 1 мм, То = 300 K ствуют фазовым переходам в материале образца, то и наибольшие изменения в спектральных функциях будут соответствовать случаю возбуждения акустических сигналов в среде, где происходит фазовый переход при поглощении лазерного импульса. Аналогичный результат для объемных волн был получен в [3].

Расчеты для других металлов (алюминия, меди, железа, никеля), выполненные для тех же условий, не выявили существенных изменений в спектре возбуждаемых импульсов нормальных волн, поскольку при Т о = 300 К ТКЛР изменяется незначительно.

Экспериментальная проверка теоретических расчетов производилась с помощью стенда, описанного в работе [8]. Результатами исследования являются дисперсионные кривые, а также формы акустических импульсов, возбужденных импульсным лазером, зарегистрированных серийным пьезоприёмником.

Некоторые результаты показаны на рис. 3 и 4, из которых видно, что собственная частота колебаний пьезоприёмника может не совпадать с квазичастотой ν акустических импульсов волн Лэмба. Длительность импульсов и число колебаний в них для симметричных волн примерно в три раза меньше, чем для антисимметричных. Связано это, очевидно, с особенностями лазерной генерации волн Лэмба. С увеличением толщины пластины независимо от квазичастоты колебаний амплитуда импульсов симметричных волн уменьшается, их длительность увеличивается. Для антисимметричных волн - наоборот.

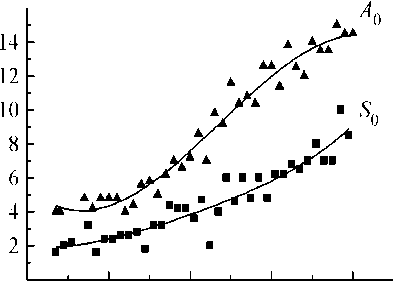
Для определения влияния магнитного фазового перехода на параметры импульсов волн Лэмба были проведены температурные исследования на пластине из ферромагнитного сплава инварного состава 32НКД, точка Кюри которого равна 210° С (рис. 5). Из полученных результатов видно, что имеет место нелинейное увеличение амплитудного значения импульсов примерно в семь раз. Существенных изменений формы импульсов, их длительности и квазичастоты колебаний при нагревании пластин не наблюдалось.

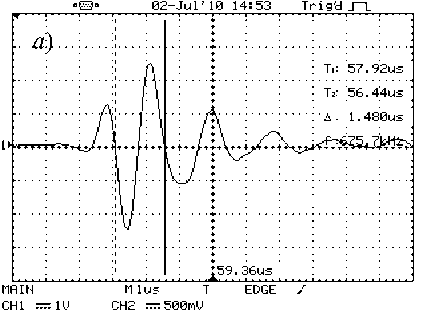
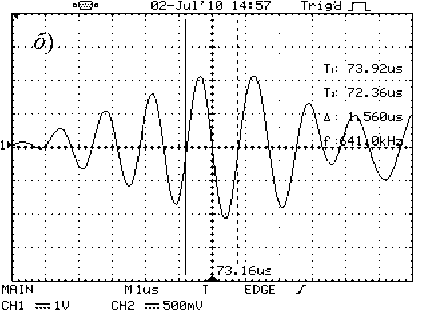
Рис. 3. Импульсы волн Лэмба в пластине h = 0,60 мм и v = 0,60 мГц: а – антисимметричные; б – симметричные

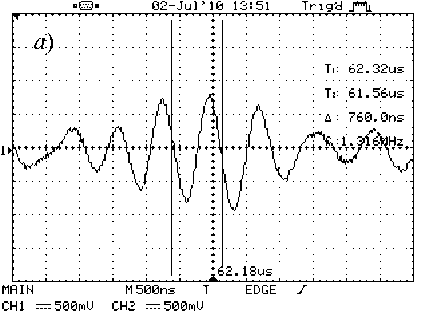
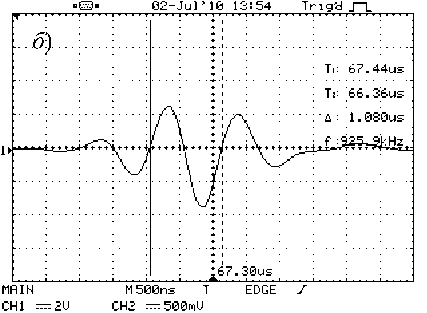
Рис. 4. Импульсы волн Лэмба в пластине h = 1,5 мм и v = 1,25 мГц: а – антисимметричные; б – симметричные

и

и , м/с

U, В

0     100    200    300    400 Л С

Рис. 5. Зависимость амплиту^ы импульсов симметричных ( S ₀) и антисимметричных

м/с

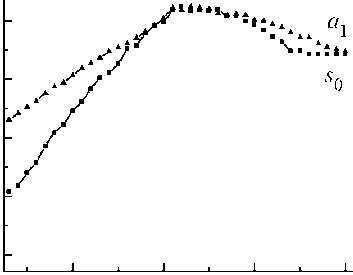
- 4600

- 4400

- 4200

- 4000

100     200     300     400 Т, °C

Рис. 6. Зависимость сре^ней групповой скорости симметричных ( S ₀) и антисимметрич-

( A 0 ) мод волн Лэмба от температуры.

ных ( A 0 ) мод волн Лэмба от температуры.

h = 0,60 мм и v = 0,60 мГц

h = 1,5 мм и v = 1,25 мГц

Известны способы оценки физико-механических свойств ферромагнитных металлоизделий, основанные на измерении скоростей акустических волн различных видов. Для определения влияния температуры на скорость волн Лэмба было проведено соответствующее экспериментальное исследование, результаты которого представлены на рис. 6. Видно, что скорости симметричных и антисимметричных волн Лэмба в ферромагнитной пластине инварного состава с повышением температуры увеличивается по линейному закону, достигает максимума в области точки Кюри и затем уменьшается. Такое поведение температурной кривой аналогично температурной зависимости продольных волн, полученной ранее [9]. На рис. 10 видно, что увеличение скорости в диапазоне от комнатной температуры до 250° С составляет примерно 12 %. Хорошо

Гуревич С.Ю., Голубев Е.В., Волны Лэмба в ферромагнитных металлах: Петров Ю.В.лазерная генерация и электромагнитная регистрация прослеживается точка перегиба, соответствующая магнитному фазовому переходу. Изменение толщины пластины и квазичастоты акустических колебаний на температурную зависимость скорости волн Лэмба существенного влияния не оказывает.

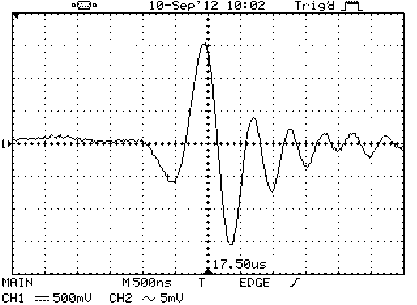
Рис. 7. Электромагнитный импульс, наве^ён-ный в ЭМА приёмнике модой У ₀ волны Лэмба

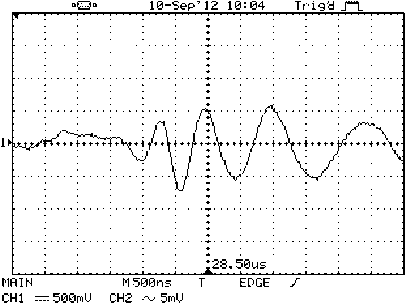
Рис. 8. Электромагнитный импульс, наве^ён-ный в ЭМА приёмнике модой A 0 волны Лэмба

Как уже отмечалось, контактные методы регистрации волн Лэмба не могут быть использованы для высокоскоростного и высокотемпературного ультразвукового контроля металлоизделий. В связи с этим авторами настоящей статьи была разработана методика и аппаратура для бесконтактной (электромагнитной) регистрации волн Лэмба. Теоретические основы этого процесса можно найти в работе [10]. Эксперимент проводился на стенде, описанном в работе [11].

Учитывая, что проведенные исследования являются довольно объемными, в статье приводятся результаты, относящиеся только к одной пластине. При этом считается, что параметры электромагнитных импульсов, наблюдаемых на экране дисплея осциллографа, пропорциональны соответствующим параметрам у.з. импульсов.

На рис. 7, 8 приведена осциллограмма электромагнитных импульсов, наводимых в электромагнитоакустическом приёмнике волнами Лэмба,распространяющимися в пластине толщиной 0,6 мм. Тип и номер возбуждаемых в пластине у.з. волн Лэмба определялись по методике, предложенной авторами в работе [8]. Из результатов экспериментов и расчетов следует, что при лазерной генерации акустических волн в ферромагнитной металлической пластине широкополосный ЭМА-приёмник регистрирует импульсы симметричных S0 и антисимметричных A0 у.з. волн Лэмба нулевых номеров. Для сравнения максимальной амплитуды U, длительности т, средней частоты колебаний (v) и формы этих импульсов, на рис. 7 и 8 приведены их осциллограммы с меньшей временной разверткой. Видно, что форма импульсов различается, амплитуда импульса симметричных у.з. волн значительно больше, чем антисимметричных, разница в длительности импульсов небольшая, а квазичастота колебаний практически одинакова. Наблюдаемые отличия связаны, очевидно, с особенностями лазерной генерации волн Лэмба.

Для оценки ширины частотного спектра возбуждаемых лазером у.з. импульсов с помощью Фурье-преобразования был рассчитан спектр импульса симметричных волн (рис. 9). Видно, что вся энергия у.з. импульса, длительность которого равна 2,9 мкс, практически заключена в пределах от 0 до 1,75 МГц с максимумом амплитуды на частоте « 1,0 МГц. В то же время у оптического импульса, длительность которого » 30 нс, верхний предел частотного диапа-

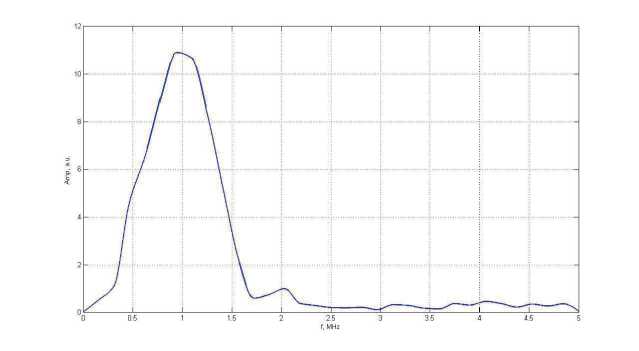
Рис. 9. Спектр электромагнитного импульса, наве^ённого в ЭМА приёмнике модой У ₀ волны Лэмба.

зона ограничивается ≈ 30 МГц. Такое уменьшение частоты означает, что металл хорошо пропускает низкочастотную часть спектра у.з. импульса (до 2,5 МГц) и интенсивно поглощает его высокочастотную (больше 2,5 МГц) часть.

Из анализа полученного спектра следует, что, когда необходимо получить максимальную амплитуду наведенного электромагнитного импульса, например, для реализации теневого или эхо- методов контроля, целесообразнее использовать резонансный ЭМА-приёмник. Его высокочастотный индуктор выполняется в виде эквидистантной решетки с шагом равным половине длины волны. На частоту спектра, соответствующую максимальной амплитуде, индуктор настраивается подбором числа витков. Резонансный ЭМА-приемник может подключаться непосредственно к входу усилителя стандартного дефектоскопа.

Информацию, полученную в ходе проведенного исследования, можно применить для создания оптимальных бесконтактных методов и средств акустического контроля листовых металлоизделий, либо композитных материалов на основе листового металлоизделия, когда излучателем ультразвука является импульсный лазер, а приёмником – электромагнитоакустический преобразователь.

Авторы выражают признательность Шульгинову А.А. за помощь в работе и обсуждение полученных результатов.

• 1.    Даниловская, В.И. Температурные напряжения в упругом полупространстве, возникающее вследствие внезапного нагревания поверхности / В.И. Даниловская // Прикл. матем. и механика. – 1950. – Т. 14, № 3. – С. 129–133.

• 2.    Гусев, В.А. Лазерная оптоакустика / В.Э. Гусев, А.А. Карабутов. – М.: Наука, 1991. – 304 с.

• 3.    Возбуждение ультразвука в железе при фазовом переходе под действием лазерных импульсов / Г.А. Буденков, С.Ю. Гуревич, А.Д. Каунов, А.Ф. Маскаев // Акуст. журн. – 1983. – Т. 29, № 4. – С. 561–562.

• 4.    Гуревич, С.Ю. Основы теории и практического применения высокотемпературного ультразвукового контроля ферромагнитных металлоизделий: автореферат дис. … д-ра техн. наук / С.Ю. Гуревич. – ^елябинск: Изд-во ^еляб. гос. техн. ун-та, 1995. – 43 с.

• 5.    Голубев, Е.В. Лазерная генерация поверхностных акустических волн в ферромагнитном металле / Е.В. Голубев, С.Ю. Гуревич, Ю.В. Петров // ФММ. – 2004. – Т. 97, № 2. – С. 8–12.

• 6.    Голубев, Е.В. К теории возбуждения волн Лэмба в металлах импульсным лазерным излучением / Е.В. Голубев, С.Ю. Гуревич, Ю.В. Петров // Акустич. журнал. – 2011. – Т. 57, № 5. – С. 600–606.

• 7.    Ландау, Л.Д. Теория упругости. Теоретическая физика: в 10-ти т. / Л.Д. Ландау, Е.М. Лифшиц. – М.: Наука, 1987. – Т. VII. – 248 с.

• 8.    Петров, Ю.В. Экспериментальное определение параметров волн Лэмба при их лазерной инерции / Ю.В. Петров, С.Ю. Гуревич, Е.В. Голубев // Дефектоскопия. – 2010. – № 3. – С. 45–49.

• 9.    Температурные зависимости скорости распространения продольных ультразвуковых волн в сталях / С.Ю. Гуревич, Ю.Г. Гальцев, А.В. Каунов, Р.С. Каримов // Дефектоскопия. – 1987. – № 2. – С. 47–52.

• 10.    Комаров, В.А. Теория физических полей: в 3 т. / В.А. Комаров, В.Ф. Мужицкий, С.Ю. Гуревич. – ^елябинск–Ижевск: Издательство ЮУрГУ, 2000. – Т. III. – 627 с.

• 11.    Экспериментальная установка для регистрации импульсных электромагнитных полей, возбуждаемых волнами Лэмба в магнитополяризованной металлической пластине / С.Ю. Гуревич, Ю.В. Петров, Е.В. Голубев, А.А. Шульгинов // Вестник ЮУрГУ. Серия «Математика. Механика. Физика». – 2012. – Вып. 7. – № 34(293). – С. 146–149.

Гуревич С.Ю., Голубев Е.В., Петров Ю.В.

LAMB WAVES IN FERROMAGNETIC METALS: LASER EXITATIONAND ELECTROMAGNETIC REGISTRATION

S.Yu. Gurevich ¹ , E.V. Golubev ² , Yu.V. Petrov ³