Волны, описываемые краевой задачей на присоединенном уравнении Гельмгольца

В работах [1–4] показано, что в экранированных волноводах с неоднородным заполнением наряду с собственными волнами могут существовать присоединенные к источнику несобственные волны, описываемые краевыми задачами на присоединенном уравнении Гельмгольца, под которым понимается уравнение с правой частью, являющейся решением однородной краевой задачи на том же самом уравнении, но с нулевой правой частью. Такие краевые задачи являются самосогласованными, поскольку в них учитывается обратное влияние возбуждаемого поля на первичный источник и волновые числа в функциях поля и источника совпадают. Источники указанного вида можно классифицировать как источники типа бегущей волны, находящейся в синхронизме с возбуждаемым ей полем. Постоянная «подпитка» поля распределенным (бегущим) источником приводит к его (поля) линейному нарастанию в направлении распространения. Возникает эффект, подобный взаимодействию волноводного поля с полем пространственного заряда, наблюдаемый в лампе бегущей волны. Можно предположить, что эффект возбуждения распределенным источником присоединенной волны должен наблюдаться не только в неоднородных направляющих структурах.

Рассмотрим круглый экранированный волновод. Сформулируем для него присоединенную краевую задачу. Она состоит из уравнения:

д ² п Z’ m д r ²

1 дп e, m 1 д ² п z m r д r     r ² дф ²

2 e , m + д - !  + бцю 2 П e , m = д z 2

(1)

= Ae’mJn (ae’mr) cos nфe-iвz, которое в соответствие с [3; 4] будем называть присоединенным уравнением Гельмгольца, и граничных условий:

m

П ^ ( r = a ) = 0; -z- ( r = a ) = 0,              (2)

д r соответствующих задачам Дирихле и Неймана. В (1), (2) П^’m — продольные компоненты электрического и магнитного векторов Герца; Jn (ae’mr) - функция Бесселя; а — радиус волновода; ae и am — корни уравнений (2).

Запишем решения вышеуказанных краевых задач в виде:

П e , m = C e , m J /a e , m r ) + D e , m I - iz lx ^{z                  n} \         / I 2B J

t / e.m \    e.m / e.m \           — iвz x Jn la , r 1 + p , I a , r I cos n ф e p , где Ce,m и De,m – произвольные на начальном этапе постановки присоединенной краевой задачи амплитудные коэффициенты, на которые в дальнейшем будут наложены условия, обеспечивающие удовлетворение решения (3) уравнению (1); pe,m (ae,mr) — частные решения неоднородного дифференциального уравнения:

f

R -( r ) + -R ■ ( r ) + «

^^^^^^в

2 ^

r

R ( r ) = J n ( a r ) ,

то есть

p- , m + 1 p« , m + r

( a e, m ) 2

—

n ² r ²

p e , m

.

= D e , ^m J_- ( a e , m r ) .

В уравнениях (4), (5) штрих означает дифференцирование по радиальной координате r .

Правые части уравнений (5) – решения краевых задач Дирихле и Неймана на однородном дифференциальном уравнении:

— D e , J ( a e , m r ) = A ^e , J ( a e ’ m r ) .

Из (8) видно, что решения (3) с учетом уравнений (5), (6) удовлетворяют присоединенным уравнениям Гельмгольца (1), соответствующим краевым задачам Дирихле и Неймана о возбуждении несобственных (присоединенных к источнику) волн типа Е и Н распределенным источником в виде бегущей волны при условии:

D e , m _— D e , m = A e , m

В том случае, когда

1                              .

R 4 r ) + - R'(r ) + a' r

—

„ 2 ^

■• R ( r ) = 0, r ,

совпадающим с уравнением Бесселя. Уравнение

(4) в отличие от (6) будем называть присоеди-

ненным уравнением Бесселя. Его запись в виде (5) соответствует задачам Дирихле и Неймана, решения которых записаны в виде (3). Значения a e ’ m в уравнениях (5) находятся из граничных условий (2).

Решения уравнений (5) имеют вид:

De,m = De,m ,(10)

решения (3) удовлетворяют обычному (однородному) уравнению Гельмгольца.

Граничные условия (2) приводят к уравнениям: f Ce — i^e De^ J- (aea) + pe (aea) = 0(11)

для Е-волн и fCm — izDm) J-(ama) + p‘m (ama) = 0(12)

Y n ( a r ) R ( a r ) , .

p ( a r ) = — J ( a r )   ——;—7— ^( a r ) +

^-           W (a r )     ^{v 7}

для Н -волн.

Поскольку поперечные волновые числа Е -волн удовлетворяют уравнению:

J „ ( a r ) R ( a r ) , .

+ Y _n ( a r )   ——7—7— Ma r ) ,

n

J - ( a e a ) = 0 ,

где R ( a r ) — решения уравнения (6), соответствующие краевым задачам Дирихле и Неймана; W ( a r ) — вронскиан, записываемый как

^W ( ^{a r} ) = J - ( ^{a r} ) Y - ( ^{a r} ) ^— J - ( ^{a r} ) Y - ( ^{a r} ) =      ;

na r

равенство (11) выполняется тождественно. При этом в (7) полагаем:

R(ar) = J- (aer), что обращает в нуль подынтегральные выраже-

Y_- ( a r ) — функция Неймана. В (7) p e ’ m ( a e ’ m r ) соответствуют задачам Дирихле и Неймана.

Подставляя (3) в уравнения (1), получаем:

C e , m J ( a e , m r ) + ^- J - ( a e , m r ) +

+

( “ em ) 2 — - 2

Jn

+

+

D e , m

⁺ - ^J -

r

( a e , m r )

+

+

(“ em Г — 7

Jn

+

+

+ -p

r

+

(“ em Г — - 2

p

e , m

■ e , m

( a e , m r )

—

+

ния при r = a .

Поскольку поперечные волновые числа Н -волн удовлетворяют уравнению:

J- (ama) = 0 ,(14)

для выполнения равенства (12) необходимо, чтобы p‘m (ama) = 0.(15)

Положив в (7) R ( a r ) = J_- ( a m r ) имеем: p‘ ^m ( a m r ) =

Y- (amr) J- (amr) ,.

= — J■, (amrИ '---/-------a (amr +

- (    )J      W (amr)       (

J 2- (a m r ) , _x

+ Y; (a ^m r f )----^afa ^m r ),

- (    )J W (amr) (

Выражение (16) приводим к виду:

p' m ( a m r ) =

= - J n ( a m r ) J

Yn (amr) Jn (amr) ,    .

-------у -------^a (a m r +

W (a mr)

(a mr)

+        [ J n ( a m r ) - J n - 1

( a m r ) x

x J n + 1 ( a m r ) ] Y n ( a m r ) =

+

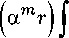
n

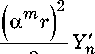
x - Jn (amr)

Y n (a m r ) J n (a m r ) ,    .

—-------^a (a m r +

W (a m r )

( a m r ) x

(amr)2

[ J n ( a m r ) ] 2 - .

Функция (17) обеспечит, если значения a m

находятся из уравнения (14), выполнение равенства (15) только при условии

-

( a m a ) 2

= 0.

Таким образом, граничное условие на экранирующей поверхности в задаче Неймана на присоединенном уравнении Гельмгольца требует выполнения равенства (18).

Итак, показано, что функции (3) при выполнении условия (9) удовлетворяют присоединенным уравнениям Гельмгольца (1). При выполнении условия (10) они удовлетворяют однородным уравнениям Гельмгольца. Для того, чтобы эти функции были решениями краевых задач Дирихле и Неймана необходимо, чтобы они удовлетворяли граничным условиям (2) на экранирующей поверхности. При этом значения a e и a m определяются как корни уравнений (13) и (14).

Рассмотренные задачи фактически являются задачами возбуждения волн в экранированном волноводе источником типа антенны бегущей волны. Волновые числа последней тождествен-

но совпадают с волновыми числами возбуждаемых волн, которые в данном случае являются несобственными, «присоединенными» к источнику волнами, не существующими без источника. Поскольку «присоединенные» волны находятся в синхронизме с возбуждающей их бегущей волной и указанные волны являются энергетически связанными, рассмотренную задачу следует называть самосогласованной.

Таким образом, для направляющих структур наряду с обычными краевыми задачами о собственных волнах могут быть сформулированы задачи о волнах на присоединенном уравнении Гельмгольца, которые имеют линейную зависимость поля от продольной координаты за счет распределенного отбора мощности от волны возбуждения. Показано, что такая краевая задача имеет решение в виде (3), удовлетворяющее присоединенному уравнению Гельмгольца и граничным условиям (2), выполняющимся для волн типа Е . Для волн типа Н в силу несовместимости уравнений (14) и (18) граничное условие (2) не выполняется, что говорит о невозможности существования в однородно заполненном экранированном волноводе волн типа Н , присоединенных к источнику.