Volume temperature control at automated high-frequency processing of polymer and composite materials

Introduction. To enhance operational and strength properties of increased durability achievement, to improve polymers and composites service life and to prevent dry start during operation, oil-filled polymer and composite antifriction materials are created using developed technology of high-frequency oil filling [1]. At the same time, implementation of the method has one problem in the course of process automation due to the need of constant sample temperature volumetric control during drying and self-filling [1–6]. Research in this field proves to be a pressing task.

Purpose and tasks. To develop a contact method for measuring a polymer sample temperature throughout the volume during high-frequency processing.

In order to achieve this goal, the following tasks were defined:

– outlining thermocouples location in the polymer sample body;

– constructing a finite-element mathematical model by calculating the effect of thermocouples quantity on the sample heating during high-frequency processing.

– constructing a general mathematical model by calculating the effect of thermocouples quantity on sample heating during high-frequency processing.

– making comparative analysis of the obtained results.

Background data . Sample from material PA6 Specification 224-001-78534599–2006; overall dimensions, 50 × 50 × 4 mm; density, 1120 kg/m3; specific heat capacity, 1601 J/kg K; thermal conductivity, 0.23 W/(m · K). Thermocouple (TС) chromel-alumel; weld diameter, 0.25 mm; wire diameter, 0.1 mm; hole dimensions, 0.25 × 25 mm [7–10].

Preliminary layout of thermocouples in the sample is shown in fig. 1.

Finite-difference mathematical calculation . Сonstruction of a finite-difference mathematical model based on the calculation of the number of thermocouples effect on the sample heating during high-frequency processing was carried out in the MSC Patran Sinda software complex (fig. 2, tab. 1).

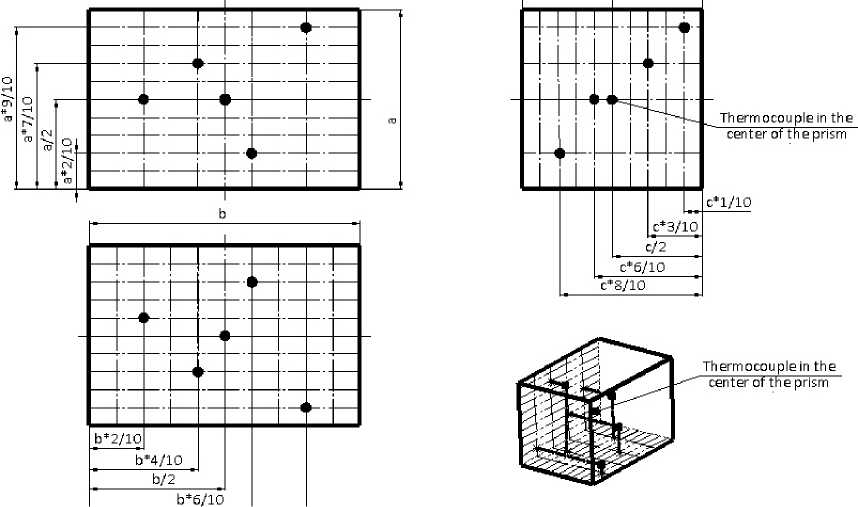
Fig. 1. Layout of thermocouples in the sample

Рис. 1. Схема расположения термопар в образце

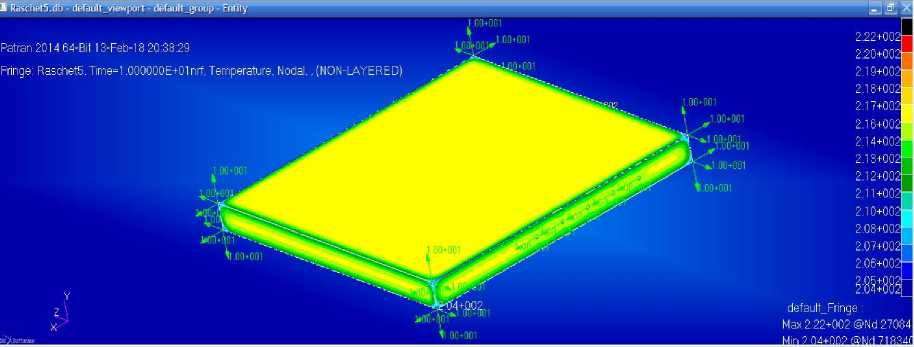
Fig. 2. The finite-difference mathematical model of the prototype

Рис. 2. Конечно-разностная математическая модель опытного образца

Table 1

Summary of calculation results MSC Patran Sinda

Quantity of thermocouples, in pcs.	Symmetry plane temperature, оС	Body surface temperature, оС	Hole walls temperature, оС
0	220.746	202.701	–
1	221.500	203.516	220.251
2	221.546	203.538	220.263
3	221.625	203.569	220.282
4	221.630	203.558	220.271
5	221.678	203.575	220.293

As boundary conditions, the following ones were adopted: volumetric heating power constant, 10 W; convective thermal conductivity coefficient constant, 10 W/(K · m2); ambient temperature, 20 оC [11–14].

According to the results of the calculations of MSC Patran Sinda given in tab.1, the diagram (fig. 3) of the temperature dependence on the number of holes for thermocouples in the polymer sample has been constructed.

From the obtained graphic data, it can be concluded that with high-frequency heating, as the number of holes in the body increases, the temperature of the polymer sample increases throughout the volume.

Calculation of error from thermocouples in polymer sample installation is done by formula

_{∆ 1 =} 100 _- T withoutTC ^⋅ 100 ₌ T 5 TC

= 100 - ^{220,746 ⋅ 100} = 0,34 %, 221,500

where Т withoutTC – temperature in the body of a polymeric sample without holes, ^оС; T 5TC – temperature in the polymeric sample body with 5 holes, ^оС.

Results of finite-element mathematical model construction showed that calculated error value does not exceed permissible value of 3 % [15].

General mathematical calculation. General mathematical model construction by calculating the effect of thermocouples number on sample heating during high-frequency processing.

The process of volumetric heating of the polymer sample with dimensions of 50×50×4 mm, from internal heat sources can be referred to as a particular case of thermal conductivity of a homogeneous plate.

Heat sources are evenly distributed throughout the volume, q v = const. Convective heat transfer coefficient, α = const and ambient temperature T air = const. Due to uniform cooling, the temperatures of both surfaces are the same [16; 17].

Under these conditions, the temperature of the plate will vary only along the x-axis (fig. 4) normal to the surface of the body.

The temperatures on the axis of the plate and on its surface are indicated through T 0 and T surface , respectively; these temperatures are unknown. In addition, it is necessary to find the temperature distribution in the plate and the amount of heat supplied to the environment according to formula

T ( x ) = T air + ^{qv ⋅δ}+ ^qv ( δ ² - x ²), α 2 ⋅λ

,

-δ ≤ x ≤ δ, where Tair – ambient temperature (air), 20 °C; – convective heat transfer coefficient, 10 W/( deg m2); λ – polymer thermal conductivity coefficient (PA 6), 0.26 W/( deg m); δ – extreme position of the point in contact with the environment, 0.002 m; qv– volumetric productivity of internal heat sources, W/m3.

Volumetric capacity of internal heat sources is calculated according to formula

Temperature field dependence, formula

T (-) = Tal r+ qv^^x air

2a

q v = Q ,

X

1-^12I 5 )

q v l52

4X

■

1 ₊f5 r

I 5

I . r

2ln -

I 5

^^^^^^B

where Q – thermal power from each internal heat source, 10 W; V – body volume, m³.

The results of internal heat sources volumetric produc tivity calculations are summarized in tab. 2.

Body surface temperature ( x = 5 )

5r < r <5,

where 5 _r - radius of the hole for thermocouple,

T , = T. + qv -⁵

surface    a rir ' a ^{.                    ( )}

0.000125 m.

Temperature difference between body surface and heat-release surface of the hole wall, formula

Symmetry plane temperature ( x = 0)

= T , + qv -⁵-0 surface 2 ^

² q_vr

T hole T surface = 4 ^

■

.

hence

5 1

5 -

^^^^^^B

2lnA_ 1 , ⁵ r

The results of temperature calculations on the surface of the body and on the plane of symmetry are summarized in tab. 3.

Let the boundary conditions of the third type be given, i. e. the ambient temperature on the outside surface and the constant heat transfer coefficient on the outside surface (fig. 5) [17–19].

₌ q v-⁵ , ²

^hole 4 X

5 1

5 -

^^^^^^B

2ln--1

5 -

surface ^{. ,}

where T hole – hole wall temperature,°С

The results of the hole wall temperature calculations are given in tab. 3, fig. 6.

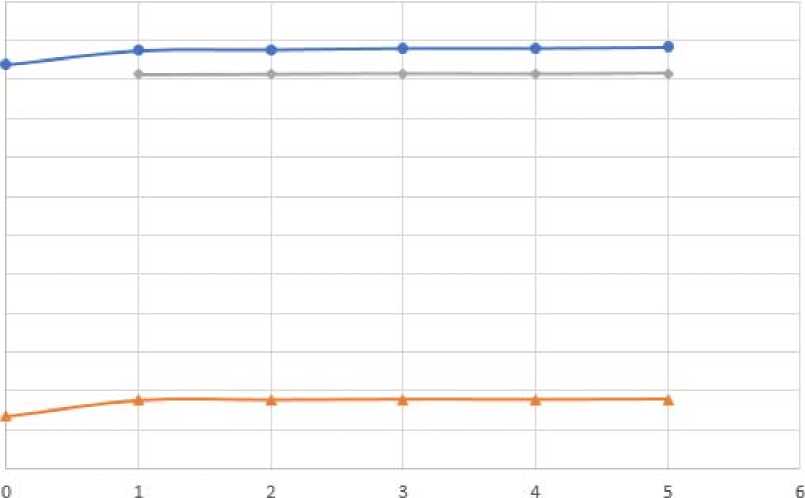
—^Temperature on the plane of symmetry, 9C—*—Surface temperature of the body, 9C—^Temperature on the wall of the hole, ^C

Fig. 3. Calculation results of MSC Patran Sinda

Рис. 3. Результаты расчетов MSC Patran Sinda

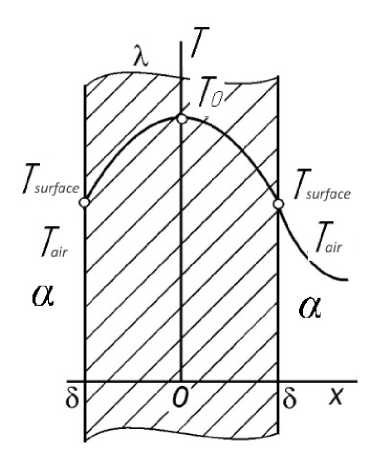
Fig. 4. Calculation scheme of thermal conductivity of a homogeneous plate

Рис. 4. Расчетная схема теплопроводности однородной пластины

Summary of internal heat sources volumetric productivity calculations results

Table 2

Quantity of thermocouples, pcs.	V , m3	q v , W/m3
0	1.00000·10–5	1.000·106
1	9.99877·10–6	1.001·106
2	9.99754·10–6	1.002·106
3	9.99631·10–6	1.004·106
4	9.99508·10–6	1.005·106
5	9.99385·10–6	1.006·106

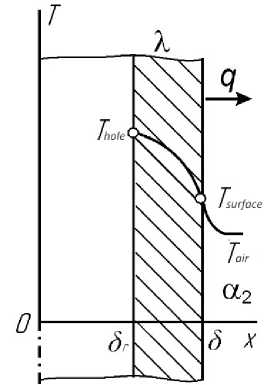
Fig. 5. Calculation diagram of the temperature on the wall of the hole

Рис. 5. Расчетная схема температуры на стенке отверстия

Table 3

The results of temperature calculations on the body surface, symmetry plane and on the walls of the hole

Quantity of thermocouples, pcs.	T surface , °С	T 0 , °С	T hole ,°С
0	220.000	227.692	–
1	220.246	227.948	224.029
2	220.493	228.204	224.280
3	220.741	228.462	224.553
4	220.989	228.719	224.785
5	221.238	228.978	225.039

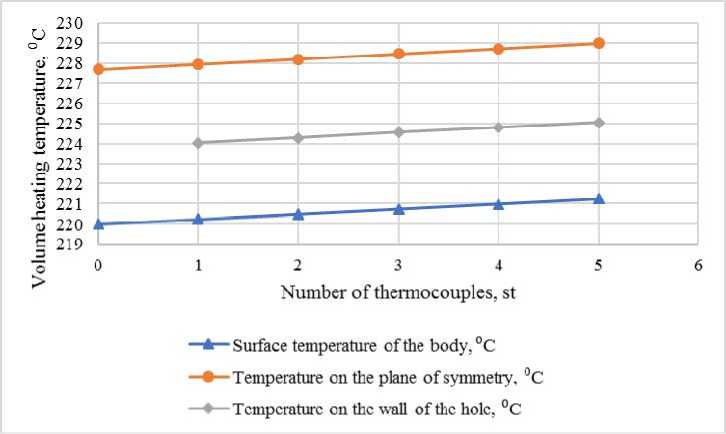
Fig. 6. Results of the General mathematical calculation

Рис. 6. Результаты общего математического расчета

From the obtained dependencies it can be seen that as the holes in the body increase, the temperature both on the surface of the sample and on the wall of the hole increases.

This can be explained by decrease in the sample volume, which entails an increase in the volumetric productivity of internal heat sources under continuous power.

Calculation of error from thermocouples installation in polymer sample (1)

A

₂ = 100 -

T wtthoutTC ¹⁰⁰

T 5 TC

= 100 -

2 69       = 0,57 %.

228,978

where Т withoutTC – temperature inside the polymeric body sample without holes, ^оC; Т 5ТC – temperature inside the polymeric body with 5 holes, ^оС.

The results of the general mathematical model showed that the calculated error value does not exceed the permissible 3 %.

Comparative analysis . Error calculation from the number of holes for thermocouples was made applying the finite-element model in the software complex MSC Patran Sinda (0.34 %) and the general mathematical model according to the calculated formulas (0.57 %). The result of the study is the compliance of the chosen method of mathematical model construction with the result of

finite-element analysis, as well as the correctness of polymer sample temperature measuring method.

Conclusion . In the present work, a method of determining the polymer sample body temperature throughout entire volume has been developed. This method has been implemented with the introduction of thermocouples into the polymer or composite body sample.

For the constructed layout of thermocouples in the body of the polymer sample to control the temperature of volumetric heating during high-frequency processing, the applicability of this scheme has been mathematically justified. Comparative analysis of measurement error due to sample volume change caused by the introduction of thermocouples not exceeding permissible 3 % [1] has been carried out.

This method has been planned for further application in automated high-frequency oil filling process [2], namely, for identification of the parameters of the filling process with a liquid plasticizer by monitoring the change in thermocouple readings.