Вопросы энергоиндексного моделирования фенологии растительности

DOI:

Фенология растительности характеризуется четырьмя основными фенологическими фазами, определяемыми переходными датами. Следующие фазы определяют динамику растительности в масштабе одного года: 1) рост (green up) – начало фотосинтетической активности; 2) фаза зрелости, в которой площадь зеленых листов достигает максимума; 3) увядание – фаза, в которой фотосинтетическая активность и площадь зеленых листьев начинает быстро уменьшаться; 4) этап бездействия (dormancy) – этап, в которой физиологическая активность растительности почти равна нулю [15].

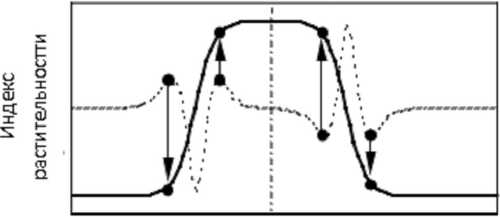
На рисунке 1 схематически показаны даты перехода с одной фазы в другую в виде минимумов и максимумов скорости изменения кривой.

Например, цикл увядания может быть охарактеризован следующей логистической функцией [10; 15; 17; 18]:

• У^ ^ 1 + exp (и И^- bt) , (1)

где t – время, дни; y ( t ) – значение вегетационного индекса в момент t ; a , b – параметры, определяемые путем подбора; ( c + d ) – максимальная величина вегетационного индекса; d – предыдущее значение этого индекса.

Вместе с тем одна логистическая функция характеризует лишь один переход фаз с двумя датами перехода. В работе [4] была предложена двойная логистическая модель. Та- кая модель, согласно [4], имеет некоторые преимущества, по сравнению с моделями на базе сплайнов и гармоническими моделями [9; 12].

В сдвоенной логистической функции фазы созревания (озеленения) и увядания характеризуются различными сигмоидальными функциями, а физический смысл параметров связаны ростом и увяданием растительности. Двойная логистическая модель имеет следующий вид:

Л0=Д1+л2х i

(1 + ехр[— m^(t — Mi)]   1 + ехр[—Mi₂(t — м₂)]) ,(2)

где f ( t ) – вегетационный индекс в момент t ; A ₁ и A ₂ – значения фона и амплитуды вегетационного индекса; ( m ₁и n ₁) ( m ₂и n ₂) – пары параметров, характеризующих фазы роста и увядания растительности соответственно; n ₁ и n ₂ – даты максимума роста и увядания в сигмоидальной функции; m ₁ и m ₂ – определяют покатость формы сигмоидальных функций.

Вместе с тем модель (2) используется обычно применительно к вегетационных индексам. Растительность является энергонасыщенным объектом и переходы с одной фазы фенологии в другую фазу будучи по сути переходом с одного энергетического состояния в другое, не могут быть охарактеризованы таким понятием как амплитуда. В предлагаемом энергофенологическом подходе если f(t) в уравнении (2) интегрировать по t, то есть по всему фенологическому периоду (то есть за год), в принципе мы должны получить всю кажущуюся энергию, выдаваемую растительностью в окружающий мир. В таком случае f(t) можно рассматривать в качестве мощности растительности, и далее, считая A12 и A22 некоррелированными мощностьями переписать выражение (2) в виде

/(t) = 4? + ^ X

1                         1

1 + expl-m^t — Mj)] 1 + exp[-m2(t — n2)]

где A ₁, A ₂ – соответственно амплитуда фона и амплитуда растительности.

Вместе с тем модели типа (2) и (3) могут охарактеризовать одну конкретную растительность при надлежащем подбора параметров A ₂, m ₁, n ₁. В случае если требуется охарактеризовать группу однотипных растений возникает вопрос о необходимости обобщения этих моделей применительно по всем растениям. В этом смысле определенный интерес представляет вопрос о потенциальной возможности модели (2) в смысле достижения экстремума интеграла второй составляющей на правой стороне (2), то есть следующего выражения:

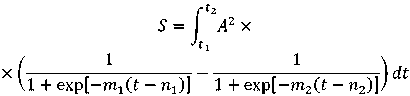
. (4)

По сути показатель S определяет ту энергию колоколо-образного импульса формирующегося в результате вычитания двух сигмоидальных импульсов в выражении (4). В общем случае задача оптимизации, то есть выбора такой взаимосвязи параметров, входящих в (4), при которой S достиг бы экстремума, может быть разделена на две задачи:

• – оптимизация на этапе перехода на фазу роста;

  

  День годa

  Рис. 1. Даты перехода фенологических фаз:

  точки – даты перехода; пунктиры – экстремумы скорости перехода фаз Примечание. Источник: [15].

  
  

  – оптимизация на этапа перехода на фазу увядания.

Вместе с тем предлагаемый энергоиндексный подход подразумевает также учета энергосвязанности используемого вегетационного индекса в фенологическом фазировании развития растительности. В качестве такового индекса могут быть взяты NDVI и LAI. Однако, как нам представляется, эффект насыщения NDVI при высоком содержании хлорофилла листьях делает этот индекс малопригодным при энергоиндексном подходе к фенологии. Следовательно, более рациональным выбором можно считать использование индекса LAI в указанных целях. Проанализируем вопрос об энегосвязанности индекса LAI.

Как отмечается в работе [14], индекс листовой площади (LAI) количественно определяет взаимосвязь атмосферы и кроны растения, в частности масштабы обмена скрытых и осязаемых тепловых потоков и СО2 между ними. Согласно [1–3; 8; 13], LAI и фракционный показатель покрытия (кроны) растения являются необходимыми данными для текущего мониторинга состояния развития растений и валидации данных дистанционного зондирования. Измерение временной динамики LAI также используется для калибровки параметров моделей начального развития растений для прогнозирования объемов биомассы [11].

По определению, LAI является отношением односторонней площади листьев к единой площадь земной поверхности. Индекс площади растительности PAI определяется как

PAI = LAI + SAI, (5)

где SAI – индекс площади ствола и веток растительности. Показатели PAI и SAI, так же как LAI, являются безразмерными показателями и характеризуют долю покрытия площадей соответственно всей растительности, листьев и ствола и веток единой площади земной поверхности.

LAI является важным энергосвязанным показателем для исследования фенологии растений [6]. Для выяснения связи LAI с фенологическими показателями роста растений рассмотрим некоторые известные базовые положения этой связи.

Согласно [5; 7], фенологическое состояние растительности P линейно связано с та- ким показателем как FPAR (доля фотосинтетически активной радиации, принимаемая растительностью), то есть

P = f (FPAR),                 (6)

где функция f ( x ) определяется следующим образом:

/         0, если х <  x_min

\ X ^Tnin

f(x) = ) —~----' ^{если Xmin < x} . (7)

I *m ^min

V           1, если x > x_max

Согласно работам [5; 7; 16], биофизическое состояние LAI м2м-г связано с FPAR через модель захвата световой радиации следующим уравнением:

_t FPAP

LAI =

In(l — FPAR_sat) maxlv ^,

где f_v – показатель доли растительности; FPAR_sat – значение FPAR при LAI = LAI mах .

Далее, с учетом вышеизложенного рассматриваются решения ряда оптимизационных задач, вытекаемых из предлагаемого энергоиндексного подхода фонологическому фазированию развития растительности.

Материалы и методы

Рассмотрим первую из вышеуказанных задач оптимизации. Введем на рассмотрение функцию

A ₂ = f ( m ₁). (9)

Физический смысл которой заключается в выборе крутизны перехода к фазе роста в зависимости от величины амплитуды v ₂.

В качестве целевого функционала рассмотрим следующее выражение:

tmax x dt

A^t)                  .

1 + exp^Ct-nJ]

Для решения данной задачи применим к функции (9) следующее ограничительное условие:

.      (11)

tmin

Физический смысл ограничения (6) заключается в следующем. При возникновении крайне благоприятных условий роста растений показатели A ₂ и t оказываются прямо пропорциональными, то есть чем больше скорость, тем больше A ₂. Однако, в реальном случае прямо пропорциональна линейная связь между t и A ₂ часто нарушается в другую сторону вокруг указанных прямых линий (рис. 2).

С учетом выражений (10) и (11) составим целевой функционал безусловной вариационной оптимизации F ₁, условно приняв t _min = 0.

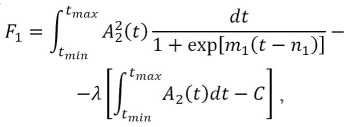
где λ – множитель Лагранжа.

группы 1, показанных на рисунке 2. Рассмотрим процесс перехода к фазе деактивации. В этом случае целевой функционал, соответствующий функционалу (7) будет иметь вид

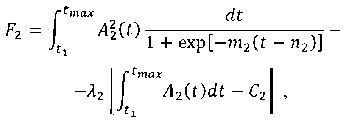
где                ; t1 – точка преломления на зад нем фронте колоколообразного импульса, показан- ного на рисунке 1.

Решение задачи (15) удовлетворяет условию

2Л2(0

----------^ -^2 = о

1 + exp[-m2(t — п2)]

Из выражения (16) находим

Решение задачи (12) должно удовлетворить условию

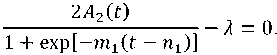
Из выражения (13) получим

Л[1 + exp[-mx(t - nx)]] ^(0 = ------------ .   (14)

При решении (14) F ₁ достигает минимума, так как производная выражения (13) по A ₂( t ) оказывается положительной величиной. Таким образом, при решении типа (14) следует ожидать минимального объёма выделяемой энергии, а следовательно, в этом случае можно рекомендовать выбор функций A ₂( t ) из

42W = Л2[1 + exp[-m2(t - «2)]].    (17)

При решении (17) функционал F ₂ достигает минимума, т.к. производная (16) по A ₂( t ) оказывается положительной величиной. С точки зрения достижения высокого энергофенологического показателя F ₂ должна иметь минимальную величину.

Следовательно, в фазе роста, то есть в промежутке (0 – t ₁) функция A ₂( t ) должен иметь возрастающий вид, а в диапазоне ( t ₁ – t _max ) убывающий. Такой порядок изменения амплитуды A ₂ во времени может оптимизировать энергофенологическую активность растительности.

Таким образом, как видно из выражений (6)–(10) в интервале (FPARmax– FPARmin) по-

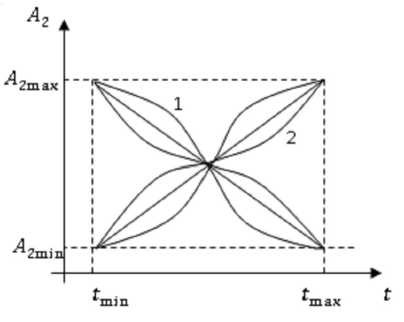
Рис. 2. Геометрическая интерпретация условия (11)

казатель «прогностическое фонологическое состояние» линейно зависит от FPAR, который инверсно-логарифмически определяет величину LAI. Следовательно, LAI может быть использован показателем фенологического состояния растительности. В выражении (8) примем:

С учетом модели (11) среднюю величину (9) определим как

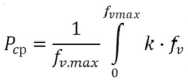
(ЧАСА СЛ]

^“P           ^dfv . (24)

\ Jv ^C2/.

где k = const.

ln(l - FPAR_sM) = Cl, LAI_max = C₂

В этом случае из (8) получаем

, , LAI Cl ln(l-FPAR/f_v)= — ~ .    (18)

Jv ^c2

Из выражения (18) находим

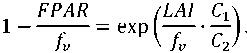
Из (19) получим

LAI fv L2/

Для вычисления оптимальной функции Ψ( f_v ) наложим на эту функцию следующее ограничительное условие:

. (25)

“'0

С учетом выражений (24) и (25) можно сформировать задачу безусловной вариационной оптимизации, целевой функционал которой имеет вид

FPAR = fv

1 — exp

C учетом (6) и (20) находим

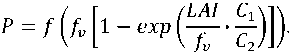
Таким образом, с увеличением LAI показатель P прогностического фенологического состояния экспоненциально уменьшается.

Вместе с тем определенный интерес представляет следующий вопрос: Каким образом может повлиять на показатель P функциональная зависимость LAI от f_v . Следовательно, для исследования данного вопроса необходимо принять вероятностную модель и далее исследовать зависимость P от вводимой функции

LAI = Ч^) .          (22)

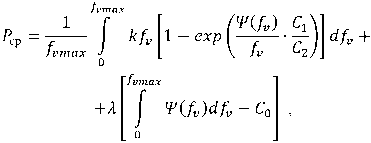
где λ – множитель Лагранжа.

Решение задачи (26) должно удовлетворить условию

^d \t^L’ [l-exp СЦЯ • ^] + MAL,)] \Jvmax L \                         — Л■ (27)

                 ; (27)

^ * fv    ^(.fv^iX Q

-7---MP 77— ‘7—7 + 2 = 0. (28)

Из выражения (28) получим

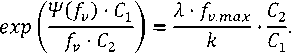
Логарифмируя (29), находим

Для упрощения математической записи в первую очередь примем равновероятную модель f_v , то есть

^Ш = 7^ • In (^-Ь^А. ^ ₌ c₃f_v , (30)

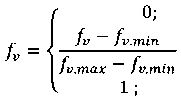
где

C3

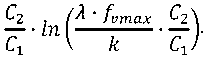
Таким образом, при решении (30) показатель P _ср достигает экстремальной величины.

где

.

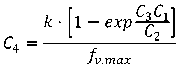
Заключение

Предложен энергоиндексный подход к фазированию этапов развития и деактивации растительности, базирующийся сдвоенном сигмоидальном модельном представлении фенологического цикла.

Определены оптимальные законы изменения амплитуды модели в фазах развития и деактивации при которых выделяемая расти- тельностью энергия в окружающую среду может достичь максимума.

Исследование связи LAI с фенологичес- кими показателями растений, в частности прогностическим фенологическим состоянием растительности Р показало, что несмотря на инверсно-логарифмическую связь между LAI

FPAR f v

и

, благодаря прямой зависимости Р и

FPAR, усредненная по всевозможным значе- ниям fv значение Р растет при наличии прямой связи между LAI и fv.