Вопросы оценки некоторых параметров при моделировании процессов производства и восстановления изделий из жаропрочных сплавов

Задачи сервиса, связанные с восстановлением работоспособности машин, агрегатов и отдельных деталей особенно актуальны для отраслей, в которых предъявляются высокие требования к надежности техники. Особо сложными являются задачи восстановления ресурса и надежности высокотехнологических изделий, к которым, например, относятся литые охлаждаемые лопатки газотурбинных двигателей. Решение таких задач требует основательной теоретической и экспериментальной проработки многих вопросов материаловедения в части получения материала с заданными свойствами при производстве изделия, снижения характеристик материала при эксплуатации из-за накопления дефектов, восстановления характеристик материала, ресурса и надежности изделия при производстве ремонтных работ.

Эффективным способом восстановления структуры и свойств монокристаллических лопаток газотурбинных двигателей из жаро- прочного сплава ЖС6У, как отмечают авторы [1], после длительной наработки является горячее изостатическое прессование в сочетании с восстановительной термической обработкой. Этот процесс требует особого внимания к соблюдению технологического режима, поскольку из-за пластических деформаций, возникающих в сплаве при горячем изостатическом прессовании, может начаться рекристаллизация, которая приведет к нарушению монокристаллической структуры сплава.

Эксплуатационные характеристики изделия снижаются из-за накопления дефектов и других повреждений в материале. Основной причиной накопления дефектов в литых монокристаллических лопатках является ползучесть. Накопление дефектов из-за ползучести происходит в γ-матрице жаропрочного сплава, и эти дефекты затем развиваются в микротрещины и поры. Процессы накопления дефектов приводят к исчерпанию ресурса изделия. При ползучести решеточные дисло- кации взаимодействуют с границами раздела фаз, образуя сетку на межфазных границах γ и γ′ фаз. При этом энергия межфазных слоев растет, за счет этого микроструктура сплава становится нестабильной. Формирование неравновесных границ раздела при взаимодействии с решеточными дислокациями может привести к появлению микротрещин на межфазных и малоугловых границах зерен в местах скопления дислокаций [2]. К повреждениям также относят и диффузионное огрубление частиц упрочняющей γ′-фазы по механизму Лифшица-Слезова [3], а это, в свою очередь, сопровождается снижением долговечности жаропрочного сплава. Вследствие постепенной деградации микроструктуры в ходе накопления повреждений происходит ухудшение механических свойств сплава и эксплуатационных характеристик лопаток. Например, после наработки в 700–800 часов начинается монотонное снижение сопротивления усталости жаропрочного сплава.

Способ высокотемпературной термовакуумной обработки используется для устранения нежелательных изменений структуры сплава лопаток, возникающих после определенного времени эксплуатации газотурбинных двигателей. Целью этой обработки является повышение ресурса лопаток. Рассматриваемый способ представляет собою фактически повторную термическую обработку изделия в вакууме (как защитной среде), которая включает гомогенизацию, т. е. образование твердого раствора с полным растворением вторичных огрубленных выделений γ^′ -фазы, и старение, которое обеспечивает формирование оптимального структурного состояния γ^′ -фазы в матрице. При гомогенизации происходит также отжиг и релаксация дислокаций, накопленных из-за ползучести. Метод высокотемпературной термовакуумной обработки позволяет почти полностью восстановить размеры и морфологию γ^′ -фазы, а также устранить дефекты, образующиеся из-за ползучести, путем отжига. Свойства материала лопаток при этом частично восстанавливаются, но начальных эксплуатационных характеристик достичь не удается.

Это происходит из-за того, что метод высокотемпературной термовакуумной обработки не позволяет повышать плотность материала и снижать его пористость [1]. Кроме того, изменение размера микропор может привести к крайне нежелательному результату, а именно к увеличению среднего размера пор. В то же время ремонтно-восстановительная обработка должна быть нацелена на устранение таких эксплуатационных повреждений, как поры, рыхлость, внутренние трещины, скопления дислокаций. Эту задачу, по мнению авторов [4], решает операция горячего изостатического прессования.

В [5] рассмотрено влияние давления на область гомогенности промежуточных фаз. Было показано, что равновесные атомные объемы компонентов сплава уменьшаются при увеличении давления. Для некоторых систем наблюдается следующая закономерность: компонент с большим атомным объемом сжимается сильнее, чем с меньшим. При повышенном давлении энтальпия сплавления оказывается меньше, что означает улучшение взаимной растворимости компонентов твердого раствора. Кроме того, всестороннее сжатие приводит к увеличению критических температур фазовых превращений «порядок — беспорядок». Всестороннее сжатие приводит также к увеличению области гомогенности промежуточных фаз, если существование их в данной системе возможно. В [5] отмечается также, что при всестороннем сжатии может возникнуть и новая фаза, которая при отсутствии сжатия является метастабильной. Этот эффект наблюдается при исследовании фазовых диаграмм некоторых двойных сплавов под давлением. При анализе поведения сплавов под давлением с использованием методов псевдопотенциала и статических концентрационных волн, представленном в [5], не учитывалась дефектная структура твердого тела. Однако именно удаление дефектов, дислокаций, микротрещин и пор является целью изостатического прессования в сочетании в восстановительной термической обработкой [1, 4]. Это требует в теоретическом описании учета исходной и приобретенной пористости материала.

Таким образом, поставленные авторами [1, 4] технологические задачи показывают, что существенно понимание и теоретическое описание процессов кристаллизации, перекристаллизации, рекристаллизации с учетом пористой структуры материала. Попытка подобного описания была предпринята в [6]. В этой работе при принятии упрощающих предположений было показано, что пористость и усадка сплава при кристаллизации являются взаимосвязанными параметрами, которые во многом определяют ход процесса формирования структуры сплава при направленной кристаллизации. Это требует дальнейшего теоретического изучения процессов рекристаллизации, перекристаллизации и, прежде всего, кристаллизации с учетом формирования пористой структуры.

В [6] в качестве одного из блоков математической модели направленной кристаллизации использована модель пористой среды [7, 8], которая была адаптирована к поставленной задаче. Другим блоком модели является модель спинодального распада Кана-Хилларда, позволяющая описывать внутреннюю неустойчивость фазы расплава при направленной кристаллизации. Было показано, что подобное описание позволяет на модели изучать процесс формирования дендритной структуры сплава при направленной кристаллизации. Аналогичное описание внутренней неустойчивости фазы твердого раствора при гомогенизации в рамках технологических задач, поставленных авторами [1, 4], требует также учета пористости материала в дополнение к оценкам, сделанным в [5]. Предполагается, что дальнейшее уточнение модели позволит оценить влияние технологических параметров на процесс ликвации легирующих компонентов в междендритном пространстве. Это, в свою очередь, позволит наметить пути повышения жаропрочности дисперсионно упрочненных сплавов.

В модели Био [7, 8], использованной в [6], одним из определяющих параметров является «присоединенная масса», задающая поведение пористого тела при механическом воздействии на него на низких и высоких частотах. Этот параметр характеризует такое явление, как увлечение части жидкости твердым телом при движении в ней, а также торможение жидкости при ее движении относительно твердого тела. Вклад указанных процессов особенно существенен для пористых тел, пропитанных жидкостью.

Оценку «присоединенной массы» можно сделать исходя из экспериментальных данных и достаточно простых геометрических соображений. Подобного рода экспериментальные данные имеются в коллоидной химии и мембранной технологии. По этим данным поверхность скольжения отстоит от геометрической поверхности твердого тела для случая водных растворов на расстоянии порядка 15 нм

(1,5 ⋅ 10 ^-8 м) . Для круглого канала эта часть жидкости будет занимать кольцевой слой. Тогда объем жидкости в поровом канале составит π d²

V = h

• ¹4 ^,

а часть движущейся жидкости —

_{V =} π ( d - δ ) ² _h

• ²          ₄ .

Объем кольцевого слоя неподвижной жидкости составит

V₂ - V₁ = ^π ₄ h ( 2d δ - δ ² )

Относительный объем будет равен

V 1 - V 2       V 2

= 1 -

V 1           V 1

^δ ⎜ ^⎛ 2 - ^δ ⎟ ^⎞ d ⎝ d ⎠

= κ

Величина пористости твердого тела является характеристикой, которая не несет информации о поровой структуре, так как является отношением всего объема жидкости к полному объему пористого тела. Поровую структуру наиболее полно отражает величина — распределение пор по размерам. Однако эта характеристика измеряется с трудом и всегда с погрешностью, которая зависит от метода измерений и вводимых допущений, необходимых при построении аппарата обработки экспериментальных данных.

Интегральной характеристикой поровой структуры является либо дисперсность, либо удельная поверхность пор пористого тела (чем меньше размер пор, тем дисперсность материала и удельная поверхность пор больше). Для каналов круглой формы она определяется в виде

π dh

^А УД = ( n d² /4) h

4 d

Из этого определения видно, что А_УД может 1

быть оценена, как ^r , где r — характеристический размер поровой структуры. Кроме того, учет формы пор позволяет r трактовать как минимальный характерный размер. Могут быть введены и другие уточняющие положения, например, с использованием весовых коэффициентов, значения которых будут зависеть от классификации, принятой для описания структуры пористости.

С уменьшением размера пор и поровых каналов доля жидкости, принадлежащей рассмотренному выше кольцевому слою, будет увеличиваться. Эту долю неподвижной жидко- сти можно оценить исходя из массового и объемного балансов. Общая масса пористого тела составляет m=m +m , где m — полная масса пористого тела, m и m — массы твердой и жидкой частей. Средняя плотность пористого тела, пропитанного жидкостью, зависит от плотностей вещества твердого скелета (ρ) и жидкости (ρL) с учетом пористости (β):

Pcp = V = VVS- + V-(1 - в) P, + ePL , где V, Vs и VL — полный объем, объемы твердого скелета и жидкости. Полную массу пористого тела m можно представить также в виде m=m +m .a+ m .b, где m .a и m .b — массы подвижной и неподвижной частей жидкости. Из этого следует

• m V S ρ S V L . a ρ L V L . b ρ L

^P cp V V ⁺ V ⁺ V ;

здесь

V La + V Lb _- V L. _{- в}

V V .

Доля неподвижной жидкости составляет

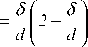
и, кроме того,

L b

- К ; -----  1

VL

^^^^^e

К .

L n_A

тогда

Из определения пористости β следует в - VL_ - VLb + VLa

VV .

Умножение этого равенства на ρ _L дает

_9o = V bb P b ₊ V_L a P_L = K V_L p _L + ( 1 ^- к } V_LP_L = ρ _L  VV V    V

^{- Ke}P L ⁺ ( 1 ^{- K} ) ^eP L

Таким образом, масса (плотность) жидкости, принадлежащей твердому скелету в виде присоединенной массы, составит

P add ^{- K}PP L (1), т е эта величина определяется пористостью β и структурой пористости, характеризуемой величиной κ

Пористость сплава определяется, прежде всего, режимом кристаллизации и последующих стадий обработки путем гомогенизации и отжига Одним из определяющих пористость параметров является величина усадки, т е различие в удельных объемах жидкой и твер- дой фаз при кристаллизации Таким образом, должна быть поставлена задача связать усадку с другими параметрами, характеризующими ход процесса кристаллизации путем описания твердо-жидкой области

Для получения необходимых оценок следует рассмотреть простую систему, содержащую два компонента A и B , в которой компонент A при кристаллизации переходит в твердую фазу, а B остается в жидкой фазе Для характеристики этой системы можно ввести некоторые соотношения:

mB q - — m A — отношение масс компонента B

( m_B ) и компонента A ( m_A ) в исходном распла-

Q - MB- ве; — отношение атомных масс компо-A нентов В и А (МВ, МА)

Выразим число и В в жидкой фазе при кристаллизации

молей компонентов А ( nAL , nBL ), состав которой будет меняться (жидкая фаза в ходе процесса обедняется компонентом А и обогащается компонентом B), mAL

M A ^,

L n_B

^mB ^L

MB , концентрацию компонента А в жид- кой фазе можно выразить как мольную долю nAL ;

c^A L . L ;

nA + nB соответственно, для компонента B:

nB

^CB ^- L , L n A ⁺ n B .

В этом случае С_А+ С_В=1 . Опустим индексы у концентраций и обозначим с мольную долю компонента А , тогда мольная доля компонента В будет равна 1–c .

Представим концентрацию с как отношение c ■ nL n, где nL — число молей компонентов A и B в жидкой фазе; соответственно, nL

здесь

mL

• ^- M L ;

mL - mL + mL и ML — условная атом- ная масса вещества жидкой фазы Выражение для МL может быть получено из следующего

c

LL

П а   _       n_A

^A   ( m L / M L )  (( m L + m B

)/ M L ) , т.е.

m^L+m^L M^L=c ^AB =c n_A^L

LL M_A^mA+M^mB

M A

B_{M B} n_A^L

MnL+MnL

AA BB

=c      _{n A} L

^L =cM A +cM B ^nB n_A^L

(2.а);

ML=cMA+cM

n B ^L n A ^L

= cM A +cM B 1—c = cM A + ( 1 — c ) M b    (2.6).

L m_A

Введем величину y ^_ m , которая представляет собою отношение массы компонента А в жидкой фазе к общей массе компонента А в системе. Поскольку

• ^mA ^{L M}A

• ^c _m L _M L ^,

(последнее выражение представляет собой формулу пересчета текущей концентрации компонента А в фазе расплава из относительной массовой концентрации в концентрацию, выраженную в мольных долях). Так как Q и q — константы ( q задается составом исходного расплава), то y = y(c) . Таким образом, в ходе процесса кристаллизации y изменяется от 1 до 0, т. е. по предположению в начале процесса весь компонент А находится в жидкой фазе и m A _ m_A (y = 1) , а в конце процесса, если вжид-кой фазе компонента А не остается, то y = 0 ; если же наступает пересыщение по компоненту B , т. е. кристаллизуется эвтектика, то y = y_* (0 < y_*< 1) , а значение c соответствует эвтектическому составу.

Поскольку по исходному упрощающему предположению в системе кристаллизуется только один компонент А , а плотность твердой фазы является величиной постоянной, то для последующих вычислений удобно ввести параметр R :

то с можно выразить через величины q и Q , т. е.

= m^LA M L = m A    cM_A+ ( 1 — c ) M B.

m^LM m^L+m^L M ; AAB   A

m

R _ -A-Ps V

(3),

c=

m A ^L m_A^L+m_B^L

[ c + ( 1 — c ) Q ]

Выразим m L через y : m L = ym A ,тогдапредыду-щее соотношение будет иметь вид

c =

ym

---Г^[ c ym A + m B ^L

⁺ ( 1-c ) Q ] .

Так как компонент B остается в жидкой фазе,

то m B _ m_B . Отсюда следует

c=

ymA ymA+mB

[ c + ( 1-c ) Q ]

^y y+ ( ^m BHA )

^{[ c+ ( 1-c} ) Q .

или

^c = y+q ^{[ c+ ( 1-c} ) Q ^] .

Из этого выражения получаем

cy + qc = cy + ( 1 — c ) Qy и y =

qc

( 1—c ) Q

или с= Qy q+Qy

где ^ρ — плотность твердой фазы (т. е. плотность компонента А в твердом состоянии, ^ρ – const ), V — исходный объем расплава (системы в жидком состоянии). Параметр R при заданном составе исходной смеси компонентов А и B является константой. Плотность жидкой фазы — величина переменная, определяется массой и объемом этой фазы

Р

mL

VL

Далее введем величину, которая представляет собою относительную усадку сплава при кристаллизации

V - V^s - V L z _----------

V

(4),

где V ^S и V ^L — объемы твердой и жидкой фаз соответственно.

Определим плотность жидкой фазы ( ρ ^L ), поскольку эта величина фигурирует в уравнениях гидродинамики, входящих в модель [6]. Используя определение усадки (4), можем записать V ^L = (1–Z)V–V ^S . Далее необходимо получить выражение для V ^S . Для этого используем определение плотности твердой фазы ρ ^s

S

Sm

( ^{р _} V s ). Поскольку кристаллизуется один

SL компонент A, то m = mA - mA , TO, ИСПОЛЬЗуЯ

L mA определение величины y (y m ), получаем mS = mA - mAy = mA (1 - y). Из этих Соотношений следует

m S = p V^s = m A (1 - y ) и V S = m A ( 1 - y ) .

P

Используя последнее равенство, найдем отношение

V^S=VR ( 1-y ) , то P = ^{1 -} R L- y (6).

Другой величиной, определяющей наряду с пористостью β значение «присоединенной массы» ρ _add , является κ . Выше этот параметр был оценен для кольцевого слоя неподвижной жидкости вблизи поверхности твердого скеле-

та пористого тела

~ : KA = mA_ (i - y ) V V P -     "

Согласно (3) - m A - = R , поэтому P V

Vs

-V- = R ( 1 - y )

и V^S=VR(1–y) .

Определив объем твердой фазы, для объема жидкой фазы получаем выражение V ^L = V(1– z –R(1–y)) . Для нахождения ρ ^L необходимо выразить массу жидкой фазы m^L через введенные LLLL параметры: m = m A + m_s = m A + m B .

mL

Из определения y ( y = A ) m_A

m и определения q (q = B ) получаем

mA mL =ymA+qmA = (y + q) mA

Отсюда следует

.

l = m^L =     ⁽ y + q ) m A

^P V^L   V ( 1 - z - R ( 1 - y ))

В правой части этого выражения присутствует mA отношение V , поэтому, используя опреде-

ление параметра R ( r = m A ), можем записать V P ^S

P L       R ( y + q )          ,     , ,     R ⁽ y ⁺ q )

=               или P = P                (5).

P S 1 - z - R ( 1 - y )              1 - z - R ( 1 - y )

-

-

Таким образом, плотность жидкой фазы ρ ^L определяется параметрами R , q (постоянные) и переменными y и z или, поскольку концентрация компонента А в фазе расплава может быть выражена и в виде y , и в виде с , то ρ ^L определяется переменными с и z . Это, в свою очередь, позволяет согласно (1) и (5) выразить ρ _add через характерные параметры и переменные задачи. Для этого следует выразить соответствующим образом пористость β . По определению в = V L и, так как согласно (4)

V^s + V^L

V^s + V L = ( 1 - z ) V , а V L = ( 1 - z ) v - V^s и

(к =— I 2 I ).

d ( d /

При относительно малой кривизне поверх-

ности пор, т. е. при δ , этот параметр может быть представлен в обобщающем виде

5 к = Ю- , d где ϕ — коэффициент формы пор, d — характерный линейный размер (диаметр пор). Тогда для ρadd, исходя из (1), (5) и (6), можем получить выражение

« А 8 \      ^1—y 1 S

P add = ^KeP L = ^\^1-R-, P d [      1-Z J

6 SR (y + q) φρS d1–z

R ( y+q ) 1-z-R ( 1-y )

Если исходить из того, что параметр κ может быть представлен как отношение неподвижной части жидкости к общему объему жид-

VL.b кости в пористом теле, т. е. к = vl и, в свою очередь, объем неподвижного слоя жидкости — в виде -Lb = !/(vl)235 (здесь у — число пор в единице объема;ψ — величина, отражающая дисперсность, пропорциональна 1/d), то для ρadd получим выражение

P add = ^KeP L = Р⁶

х 1 1-Rl^y 1 P ^S [      1-z J

^{7(( 1-z} ) ^{-R ( 1-}y ) )]^Z _х V ( ( 1-z ) -R ( 1-y )) ^X

R ( y+q )

ψδ S V 13 ρ

( 1-z ) -R ( 1-y ) ;

13 х

[^{( 1-}z ) ^{-R (} y + q ) ]

^{( 1-}z ) ^{-R (} y + q )       ^{R (} y + q )

1-z        ( 1-z ) + R ( 1-y ) ;

Р6 s________ R ( y + q ) ________

V ^{13 P} ( 1-z ) l ( 1-z ) -R ( y+q ) ] ¹³

Сравнение выражений (7) и (8) показывает, что в (8) имеется множитель

( [ ( / - z ) - r ( y ₊ q ) ] 113 , который может интерпретироваться как поправка к оценкам, принятым в (7). В то же время выражение (7) обладает большей общностью, поскольку параметр d , характеризующий развитость поровой структуры — ее дисперсность, может меняться в процессе кристаллизации. Если в начале процесса плоская граница затравки означает, что значение d относительно велико, ρ _add — соответственно, мало, то по мере развития процесса и формирования поровой структуры твердо-жидкой области значение d уменьшается, что дает рост ρ _add . Таким образом, соотношение (7) является рекуррентным соотношением, т. е. значение d должно определяться по ходу процесса кристаллизации. Однако варьированием параметра ψ в выражении (8) можно установить, насколько необходимым является использование формы (7).

Приведенный выше алгоритм расчета оценок позволяет установить зависимость усадки z от концентрации в форме y или c по экспериментальным данным для плотности расплава при различных составах (для систем, которые удовлетворяют принятым допущениям: кристаллизация одного компонента и т. д.). Это следует из определения величины z.     v - V S - v^l , и других соотношений:

z =-----------

V

VS

S m p ,

VL

L m ^p ,

LL     SL m = m, + mR  m = m, — m.

ABAA

V —т ( m A ^— m A )—( m A ^{+ m}B )

pp т. е. z =---------------------------------

V ;

далее, используя определения mAL y = и q для z получаем mA

V —^m A ⁽ i - y )—4 m A ⁽ y ⁺ q )

z =    __________ P_________

• V ^.

Представление m в виде m = R ρ ^sV позволяет для z записать

p z = 1 — R(1 — y ) — — R (y + q )

Из (9) следует, что экспериментальная зависимость ρ ^L = ρ ^L(y) дает расчетную зависимость z = z( y ) .

Таким образом, поставленная в работе задача уточнения оценок, использованных в [6] для описания процесса направленной кристаллизации, решена. Следующим шагом исследования должна быть визуализация развития процесса с учетом полученных оценок в вычислительном эксперименте по типу выполненного авторами [9].