Восстановление быстро осциллирующих младшего коэффициента и источника гиперболического уравнения по частичной асимптотике решения

В работе поставлена и решена асимптотическая задача о (точном) восстановлении неизвестных, не зависящих от пространственной переменной сомножителей быстро осциллирующих по времени источника и младшего коэффициента одномерного волнового уравнения с младшим членом по частичной асимптотике решения.

• ^# Исследование выполнено при финансовой поддержке гранта Российского научного фонда, проект № 20-11-20141.

Для различных эволюционных уравнений многочисленные задачи об определении неизвестных источника и коэффициентов без предположения их быстрой осцилляции исследованы в теории обратных задач (об этой теории см., например, [1–3]), где в дополнительном условии (условии переопределения) фигурирует точное решение прямой задачи. Вместе с тем уравнения с быстро осциллирующими данными нередко встречаются при моделировании физических, химических и других процессов, протекающих в средах, подверженных высокочастотному воздействию электромагнитных, акустических, вибрационных и т. п. полей. Например, уравнение теплопроводности для стержня, через который пропускается высокочастотный электрический ток, вследствие чего в нем возникают высокочастотные тепловые источники; уравнение колебаний струны или стержня при воздействии на них высокочастотных внешних сил (см. задачу В. Н. Челомея о высокочастотных сжатиях-растяжениях стержня, стабилизирующих его прямолинейную форму); уравнение переноса вещества в несжимаемой жидкости при наличии высокочастотных источников; уравнение тепловой конвекции жидкости в сосуде при его высокочастотных вибрациях (см. [4–6]) и т. д. Все это свидетельствует об актуальности задач теории возмущений о точном восстановлении неизвестных функций в высокочастотном уравнении с помощью нескольких первых членов асимптотики его решения.

В данной работе рассматривается задача Коши для одномерного гиперболического уравнения, младший коэффициент и правая часть которого осциллируют по времени с большой частотой ω , причем амплитуда младшего коэффициента мала — пропорциональна ω ^-1 . Исследован вопрос о восстановлении этих быстро осциллирующих функций (точнее, их не зависящих от пространства высокочастотных сомножителей) по заданной в некоторой точке пространства четырехчленной асимптотике решения. Используется неклассический алгоритм решения такого рода задач, который применялся нами в случае параболических и гиперболических уравнений с неизвестным источником [7–9]. Этот алгоритм лежит на стыке двух дисциплин — асимптотические методы и обратные задачи. В связи с этим решение задачи о восстановлении неизвестных разбивается на две части, относящиеся к соответствующим дисциплинам, и нужно следить за согласованностью (например, в смысле гладкости функций) указанных частей. В условии переопределения при этом участвует не (точное) решение, как в классике, а лишь его частичная асимптотика определенной длины; при этом необходимая информация задается не для всех коэффициентов этой асимптотики, а лишь для некоторых «базисных» функций, которые являются либо соответствующими коэффициентами указанной асимптотики, либо их быстрыми составляющими. Так, в данной работе в постановке задачи о восстановлении (в условии переопределения) участвуют коэффициенты четырехчленной асимптотики, вычисленные в фиксированной точке пространства — это функции q o (t), q 1 (t), q ₂ (t)+ A 1 (t, wt) и q a (t) + A2(t, wt), но непосредственно задаются лишь функции q o (t), q i (t), A i (t,T ) и А 2 (t,T). Остальные функции произвольным образом задавать нельзя, так как они зависят от заданных. При такой постановке неизвестные быстро осциллирующие функции исходной задачи однозначно и эффективно определяются.

Результаты данной работы без доказательств изложены, в основном, в [10].

1.    Построение асимптотики (прямая задача)

Пусть T > 0, П = {(x, t) : x G R, t E [0; T]}, Q = {(x,t,T) : (x, t) 6 П, т 6 [0, то)}. В полосе П рассмотрим задачу Коши для гиперболического уравнения с младшим членом и большим параметром ω вида du - Hxu+ 1a^,t, ut)u = f (x, t, шt);

(1.1)

< u(x,0) = d o (x);

, ^ = d i (x).

Здесь функции f (x, t, т ) и a(x, t, т) определены на множестве Q и 2п-периодичны по т , а функции d o (x) и d i (x) определены на прямой R. Все рассматриваемые в работе функции считаются вещественными.

Для того чтобы описать условия гладкости, налагаемые на функции a и f , определим следующие линеалы. Для любого целого неотрицательного числа m символом C ^т (П) будем обозначать пространство заданных на П непрерывных функций u(x, t), обладающих непрерывными на П производными ^d g + j d j , 0 <  i + j ^ m. Символом C ^m,0 (Q) будем обозначать линейное пространство заданных на Q непрерывных функций v(x,t, т), d i + j v ( x,t,T )

имеющих непрерывные на ^ производные — дффз’ , 0 ^ ^г + j ^ m- Будем еще рассматривать аналогичный линеал C ^m (R). Отметим, что функции из указанных линеалов и их производные могут быть неограниченными.

Функции f и a представим в виде:

f (x, t, т) = F(x, t) + ф(x, t, т),   a(x, t, т) = A(x, t) + b(x, t, т), выделив в них средние относительно τ (на периоде):

2 π

^{F (x,t)} = ^{( f(x,t,т}) ) =

^ /f ( 2n J

x, t, т ) dт,

A(x, t) = ( a(x, t, т ) ) .

Пусть A,A t ,A tx E C 4 (П), A E C 2 (П)4, F,F t F& E C ⁴ (П), F _x 2 E C ² (П), b,b tx E C4 ' 0(^), ф,ф t _x E C ^4,0 (Q), d o E C 5 (R), d i E C4(R). Частичную асимптотику по ш ^ 1 решения и ш (x,t) задачи (1.1) будем строить в виде:

У4 ш (x,t) = u o (x,t) + Шu 1 (x,t) + Ш 2 ( u 2 (x,t) + V 2 (x,t, шt) ) + Ш1 4 ( u 4 (x, t) + V 4 (x, t, шt) ) + Щ1 5 V 5 (x, t, tit),

(1 . 2)

где функции U k (x,t) и V k (x,t,т ) определены на множествах П и Q, а также дважды непрерывно дифференцируемы по x и t и по x и t, т соответственно, причем v k ( x, t, т ) являются 2п-периодическими по т с нулевым средним.

В дальнейшем часто будем обращаться к следующим двум простейшим типам линейных однозначно разрешимых задач. К первому отнесем задачу о 2п-периодических решениях обыкновенного дифференциального уравнения 2-го порядка вида

' ^ЕЕ) = Ф(x.t,т );

(1-3)

< s(x,t,т + 2п) = s(x,t,т); 1(s(x,t,т)) = 0, где ^(x, t, т) — определенная на множестве Q функция, 2п-периодическая по т. Решение задачи (1.3), как известно, имеет вид:

s(x, t, T )

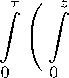
^(x, t, s) ds

-

^(x, t, s) ds

))

dz

-

M I 00

ds

-

τ

x, t, s ) ds

dz .

Ко второму типу отнесем задачу Коши для волнового уравнения в полосе П вида

U tt (x, t) - U xx (x, t) = g(x, t);

< u(x,t) | t =o = h i (x);

(1.4)

;ut(x,t)|t=o = h2(x), где функции g(x, t) и hi(x), h2 (x) определены в П и на R соответственно, причем g(x, t) и h2(x) непрерывно дифференцируемы по x и hi(x) дважды непрерывно дифференцируема (g,gx € C0(П), h2 € C 1(R), hi € C2(R)). Решение задачи (1.4) выражается, как известно, формулой Даламбера:

x + t                  t     x +( t-s )

u(x,t) = 2 ( h i (x - t) + h i (x + t) ) +2 j h2« ) d^ + 2 ^ ds j g^s") d^ x - t                  0      x- ( t-s )

При этом, если для некоторого натурального n имеют место соотношения: g, g _x ∈ C ^П-1 (П), h ₂ € C ⁿ (R), h ₁ € C ⁿ⁺¹ (R), то решение задачи (1.4) u € C ^п+1 (П).

Для любого положительного числа M определим прямоугольник П м = { (x,t) : | x | С M, t € [0; T ] } , а также введем в рассмотрение (к + 1)-членную, к = 3,4, асимптотику решения u _ω задачи (1.1):

k иш (x,t) = Uo (x,t) + ^-1u1(x,t) + ^2 Ш-s (us (x,t) + vs (x,t, wt)).          (1.5)

s =2

Теорема 1. Для каждого M >  0 имеет место асимптотическая формула:

иш(x,t)- и3ш (x,t)^C(n ) = O(w-4), Ш ^ то, где Ui(x, t), i = 0,1, 2, 3, Vj(x, t, t), j = 2, 3, являются решениями задач вида (1.4) и (1.3) соответственно.

Здесь C (П м ) — обычное банахово пространство непрерывных в прямоугольнике П м функций с max-нормой.

Замечание 1. В теореме 1 речь идет о четырехчленной асимптотике решения u _ω , поскольку именно эта частичная асимптотика требуется в § 2, и она обеспечена указанными выше требованиями гладкости данных задачи (1.1). При увеличении гладкости данных можно строить асимптотики соответствующих более высоких порядков. При бесконечной гладкости результат, аналогичный теореме 1, справедлив для полной асимптотики решения u _ω .

<1 Доказательство теоремы 1. Подставим функцию w _ш (x,t) (см. (1.2)) в равенства (1.1). Приравняем коэффициенты при одинаковых степенях ω и воспользуемся операцией усреднения по t = wt. В результате получим следующий набор задач:

d ² u o ( x,t ) ∂t ²

= F (x,t);

u o (x, 0) = d g (x); = d i (x),

(1.6)

' dv ² = Ф(x,t,т);

< V2(x,t,T + 2n) = V 2 (x,t,т); _i ( v 2 ⁽x,t,^T) ) = ⁰,

(1.7)

• • SWy) — S^ = - A(x,i)uo(x,i);

u i (x, 0) = 0;

dui(x,0) I         — dv-(x,t,T) I dt Ln дт I, „’ 1t=0                   lt,T=0

• (1.8)

d^ 3 = - 2 П-Г— - b(x,t,T)u₀(x,t); дт²              dtdT          \ , , ) ^o\

• < v a (x, t,T + 2n)= v a (x,t,T);

_i ( v 3 ^(x,t,^T) ) = 0,

• (1.9)

' 22-4^ - ^^u^ = - A(x,t)u i (x,t);

< U 2 (x,t) | t =0 = - V2(x,t,T ) | t,T =0 ;

du - ( x,t ) I      = - dv - ( x,t,T ) I - dv 3 ( x,t,T ) I

_ dt    lt=0           dt lt,T=0 дт    lt,T=0, d-V4 _ d2v2(x,t,T)    d2v-(x,t,T)    9д2v3(x,t,T)          +

ITT =     ЁХ Т          dt -        ² dtdT       ^b(x, t,^{T )u i (x}, t);

< v ₄ (x, t,T + 2n) = v ₄ (x, t,T );

_ (v 4 (x,t,T) ) = 0,

• (1.10)

• (1.11)

^d udt - x’t ) - ^d uQ ^ i’t ) = - A(x,t)u 2 (x,t) - ( b(x,t,T)v 2 (x,t,T) ) ;

< u 3 ^{(x,t) |} t =0 = ^{- v} 3 ^{(x,t,T) |} t,T =0 ;                                                 (1.12)

du 3 ( x,t ) I      = - dv 3 ( x,t,T ) I        - dv 4 ( x,t,T ) I

_ dt    lt=0           dt     lt,T=0        дт lt,T=0, d-V5 _ d2v3(x,t,T)     d2v3(x,t,T)    9d2v4(x,t,T)     , / , x /    .4

ITT = dX 2           dt -        ² dtdT      ^b(x, t, ^{T )u} 2 ^(x, t)

• ^{- A(x}, ^t)v 2 ^(x, t, ^т ) ^- ( ^b(x, t, ^{т )v} 2 ⁽x, t, ^т ) ^- ( b⁽x, t, ^{т )v} 2 ⁽x, t, ^т ) ) ) ;            (1 13)

v ₅ (x, t,T + 2n) = v ₅ (x, t, T );

_ (v5^(x,^t,T ) ) = ⁰,

^d udt - x’t ) - ^d uxxx't ) = - A(x,t)u 3 (x,t) - ( b(x,t,T)v 3 (x,t,T) ) ;

• < U 4 (x,t) | t =0 = - V 4 (x, t,T ) | t,T =0 ;                                                 (1-14)

du 4 ( x,t ) I __ dv 4 ( x,t,T ) I             dv 5 ( x,t,T ) I

. ^dt l t =0             ^dt \ t,T =0 ^dT \ t,T =0 ^.

Отметим, что (1.6), (1.8), (1.10), (1.12) и (1.14) — задачи вида (1.4), а (1.7), (1.9), (1.11) и (1.13) — задачи вида (1.3). Нетрудно проверить, что требуемая для их однозначной

разрешимости гладкость данных, о которой говорилось при описании задач (1.3) и (1.4), выполнена в силу условий, наложенных на функции a(x,t,т), f (x-t-T ), d g (x) и d i (x). Резюмируя сказанное, придем к задаче:

• 82^,) - 82.^ + "  _a(x,_t,^t) W _M (x,t) = f (x,t_M) - z(x,t,„_ii„).

' wL (x, 0) = d o (x) - ^ v s (x,0-0);                                                    ⁽¹-¹⁵)

SwL (x,0) _ л / \1_ dv5(x,0,0) dt = d1(x)   "5

где

, . x 1 Fd2V4    d2V4   nd2vs     . z.J

^z(x-t-^T-^w) =     "её ^- .... ^{+ 2} дйт ⁺ Av ^{3 + (}bv ³ - ^{< b}v ³

+ X [ a(u 4 + V 4 ) + )-^ - ^v ] +   av ₅ .    (1.16)

w5               dt2    dx2w

Зафиксируем произвольное положительное число M. Из представления (1.16) функции z(x-t-T-w') и равенств (1.6)-(1.14) вытекает асимптотическая формула:

^ ^z(x-t-T-^⁾ ^ c (П м ) = O^{(w 4 )}, ^w ^то .                      ⁽1-17)

Положим W = u _t — w _t

Придем к задаче

и вычтем из равенств (1.1) соответствующие равенства (1.15).

∂2W   ∂2W dt2      dx2

- ¹ aW + z; ω

< W (x-0-0) = ^ 1 5 C o (x);

(1.18)

sw (X2O , o)     _ip / \

, dt t5 C1(x)- где Co(x) = vs(x- 0- 0), Ci(x) = dv5(x,0,0). Считая правую ее часть известной, будем смотреть на (1.18), как на задачу вида (1.4), а потому по формуле Даламбера получим

-

x + t

W(x-t-T ) = —/■,,:.x - t) + C0(x + t) ] ■ —   C1«) d<

^W"                            2ШМ x-t

t     x +( t-s )

^bs J

(aW)(^- s- ws) d^ +

2w

t ds

x +( t-s )

(1.19)

0      x- ( t-s )

/

0      x- ( t-s )

z(^- S-Ш8^ w) d^.

Для краткости обозначим предпоследнее слагаемое в правой части (1.20) через h(x-t-w). Ясно, что для M > 0 найдется такое число шм > 0- что при w > wm hh(x-t-w)hc(Пм) < 2bW(x-t-w)hc(Пм).                      (1.20)

Из соотношений (1.19), (1.20), (1.17), (1.18) вытекает асимптотическая формула

^ u " - w ⁴" 1 с (П м ) = ^{O ( w -5 )} ’ ^w ^“ .

Указанная в теореме 1 оценка следует теперь из неравенства треугольника:

B u " ^- u " ^ С (П „ ) <  Л “ " - w " ^ C (H „ ) ⁺ 1 w " ^- u " ^ С (П „ ) = ^{O ( w -4 )} ' ^w ^ “ ■ ^

2.    Обратная задача

Пусть T >  0, П = { (x, t) : x E R, t E [0, T ] } , Q = { (t, т ) : t E [0, T], т 6 [0; то ) } .

В полосе П рассмотрим задачу Коши вида (частный случай (1.1)):

' du - Ixu + 1 B ^(x,t)p^(t,ut^)u = F^(x,t)r^(t,^^t);

< u(x,0) = d o (x);                                                             (2-1)

.          = d 1 (x).

Фигурирующие здесь функции B(x,t), F (x,t) и d o (x), d i (x) определены в полосе П и на прямой R соответственно и удовлетворяют условиям (определения используемых здесь линеалов см. в §1): B,B t ,B tx E C 4 (П), B _x 2 E C 2 (П), F,F _x 2 E C 2 (П), F _t ,F _x ,F _tx E C 4 (П), d o E C 5 (R), di E C ⁴ (R). Эти функции предполагаются известными. Положим далее

P^(t,т ) = P o ^{(t) +} P 1 ^(t,т), ^r(t,т ) = r o ^{(t) +} П⁽^^т),                  ⁽²-²⁾

где P o (t) = ( p(t, т) ) , r o = ( r(t,T)) — средние функций p и r по т на периоде. В этом параграфе функции p o , r o , p i и r i неизвестны, но обладают заданной гладкостью: p o E C 2 (R), p _i E C ^5,o (Q), r o E C 2 (R), r _i E C ^5,o (Q). Здесь линеал C ^n,o (Q) состоит из функций s(t,т), (t, т) E Q, обладающих непрерывными в Q производными по t вплоть до n-го порядка.

В данном параграфе будут описаны дополнительные условия (условия переопределения), а затем сформулирована и решена задача о восстановлении указанных неизвестных функций.

Для того чтобы получить условия переопределения, предположим временно, что функции ρ 0 , r 0 , ρ 1 и r 1 известны. Тогда данные задачи (2.1) позволяют рассматривать ее как частный случай задачи (1.1), для которой справедлива теорема 1. Так что для решения и _ш (x,t) задачи (2.1) при фиксированном M > 0 справедлива асимптотическая формула:

и _ш (x,t) -

u o (x, t) +—u _i (x, t)

+ ^ ш -k ^U k (x, t) + V k (x, t, wt)^

= О ( ш 4 ) , ш ^ то ,    (2.3)

C (Π M )

k =2

где функции U i , i = 0,1, 2, 3, и V j , j = 2, 3, являются решениями следующих задач:

■ ⁸> - ^э> = F(x.t)r o (t);

U o (x, 0) = d o (x);

(2-4)

(2-5)

(2-6)

. ^u^ = d i (x),

■ « 2 5 2 = F (x,_i)r 1 (_i.т);

< V2 (x,t,т + 2n)= V 2 (x,t,т); . ( ^v 2 ^(x,t,т) ) = ⁰,

'^д^ - i^ = - B(x,t)p o (t)u o (x,t);

U i (x, 0) = 0;

du i ( x, o)    dv 2 ( x, o , o) dt = - дт ,

' ддТ з = - 2 . - B(x,t)p i (t,T)u o (x,t);

< V3(x,t, t + 2n)= V3(x,t, t);

_i ( v 3 ⁽x,t,^T) ) = 0,

'     -      = - B (x,t)p o (t)u i (x,t);

< u2(x, 0) = -v2(x, 0, 0);(2

du 2 ( x, 0)    dv 2 ( x, 0 , 0)      dv s ( x, 0 , 0)

dt = ^- dt ^- дт ’

' ^ = - ^дЙ2 - 2 $R - S(x,t)p ₁ (t,T)U 1 (x,t);

< v4(x,t,T + 2n) = v4(x,t,T);(2

^(x, t,T ) ) = 0,

' ^ - ^xu ³ = - B(x,t')po(t')U2(x,t) - B (x,t) ( p i (t,T)v 2 (x,tT) ) ;

< и з (х, 0) = - V 3 (x, 0, 0);                                                             (2.10)

ди д ( х, 0)    dv 3 ( x, 0 , 0) dv ₄ ( x, 0 , 0)

dt = dt          дТ .

Далее функции ρ 0 , r 0 , ρ 1 и r 1 вновь будем считать неизвестными, принадлежащими указанным выше классам. Перейдем к формулировке условий переопределения. Для этого введем в рассмотрение следующие объекты:

• (1)    x o € R — точка, в которой выполнены следующие условия: F (x o ,t) = 0, B(x o ,t) = 0 при всех t € [0; T ], d o (x o ) = 0 (существование такой точки здесь предполагается);

• (2)    q o € C 5 ([0, T]) — функция такая, что q o (t) = 0 при всех t € [0; T ], q o (0) = d o (x o ), q 0 (0) = d i (x o );

• (3)    A i (t, t ) — определенная и непрерывная на множестве Q функция, 2п-периоди-ческая по т с нулевым средним, имеющая производные д 2 Т 2-, ^д ^- € C ^5,0 (Q);

• (4)    q i € C ⁴ ([0, T]) — функция, для которой q i (0) = 0, q i (0) = - ^{dA -} _d ⁽ ° ’^o) ;

• (5)    A 2 (t, т) — определенная и непрерывная на множестве Q функция, 2п-периоди-ческая по т с нулевым средним, и имеющая вторую производную по т : дТ ² € C ^5,0 (Q).

Для формулировки условия переопределения нам остается указать еще два объекта (две функции), но для этого понадобятся некоторые простые утверждения, которые опишем в виде леммы.

Лемма 1. Справедливы следующие результаты:

• 1)    задача (2.4) с неизвестной функцией r o при дополнительном условии u o (x o ,t) = q o (t) однозначно разрешима относительно (r o , u o ) ;

• 2)    задачи (2.5) и (2.7) с неизвестными функциями r i и pi и заданной uo при дополнительных условиях V 2 (x o , t,T ) = A i (t,T) и V 3 (x o ,t,T) = A ₂ (t,T) соответственно однозначно разрешимы относительно (r i , v 2 ) и (p i , v 3 ) ;

• 3)    задача (2.6) с неизвестной функцией p o и заданными u o и v ₂ при дополнительном условии u i (x o ,t) = q i (t) однозначно разрешима относительно (p o ,u i ) .

Доказательство леммы приведем ниже, а пока введем два последних объекта, необходимых для формулировки условий переопределения.

• (6)    q 2 — функция, определенная на отрезке t € [0, T] равенством q ₂ (t) = u ₂ (x o , t), где u 2 — решение задачи (2.8) с уже известными, в силу леммы 1, функциями ρ 0 , u 1 , v 2 и v 3 .

• (7)    q 3 — функция, определенная на отрезке t € [0, T] равенством q 3 = u s (x o ,t), где u 3 — решение задачи (2.10) с известными функциями ρ 0 , ρ 1 , u 2 , v 2 , v 3 и v 4 , последняя из которых является единственным решением (2.9).

Задача о восстановлении функций р и r состоит в нахождении функций p(t, т ) и r(t, т ) вида (2.2), где функции p o , r o , p i и r i принадлежат указанным выше функциональным классам, при которых решение и _ш (x,t) задачи (2.1) удовлетворяет асимптотической формуле (условию переопределения):

и _ш (x g ,t) —

q o (t) + J qi(t) + J 2 ( q ² (t) + Mt,^t) )

+A j3

( ^q 3 ^{(t) +} ^ 2 ⁽t, ^t)

= o ( j ^{- 4} ) , C ([0 ,T ])

ω → ∞ . (2.11)

Теорема 2. Задача о восстановлении функций ρ и r однозначно разрешима.

Замечание 2. Решение задачи о восстановлении функций ρ и r сводится (посредством арифметических операций, а также операций дифференцирования и интегрирования) к решению двух уравнений Вольтерра 2-го рода.

Прежде чем доказывать теорему, докажем сформулированную выше лемму.

• ⊳    Доказательство леммы 1 разобъем на пункты в соответствии с пунктами ее формулировки.

• (1) Функция r g € C ² ([0, T ]), входящая в (2.4), при дополнительном условии U g (x g , t) = q g (t) согласно формуле Даламбера удовлетворяет равенству

xo+t                 t     xo+t-s qo(t) = 2 [do(xg — t) + dg(xg + t)] +| У di(€) d^ + 2/ ds / F (£,s)ro(s) d^- (2Л2) xo-t                0     xo-t+s

Дифференцируя его дважды по t, получим уравнение Вольтерра 2-го рода (относительно неизвестной r o ):

t ro(t) + 2F(10 t) / [FX(xo + t — s,S) — FX(xo 0

— t + s, s) r o (s) ds

(2.13)

-

f (x o t) ^q o ‘ ^{(t) —} 2 [ d o ‘ ^(x o ⁺ t)⁺ do⁽x o ^— t) ] ^— 2 [ dKx o ⁺ t)⁺ dKx o ^— t) ] 2 -

В силу условий, наложенных выше на функции F , d o , di и q o , уравнение (2.12) эквивалентно (2.13), а последнее имеет единственное решение r o € C ² ([0,T]). При известной r o функция u o (x, t) однозначно находится из (2.4).

(2) Функция r i € C ^5,0 , которая входит в (2.5), при дополнительном условии

v ₂ (x o , t,T) = X1(t,T ), очевидно имеет вид r _i =

Р (^) ^{d 2} ^dTt^T) . Функция V 2 (x,t,т ) при

известной r i (t, т) однозначно находится из (2.5) (см. задачу (1.3) выше). Аналогично доказывается и второе утверждение этого пункта леммы, касающееся функций p i , V 3 . При этом

^{P 1 (t,т})       B (x o ,t)q o (t) [²

d ² A i (t,T) ∂t∂τ

d^CV) 1

⁺     дт ² J ^-

Дважды дифференцируя последнее равенство по t, получим эквивалентное равенство q,‘(t) = -1 Г d2V2(xo + t, 0,0)

d ² V 2 (x o - t, 0,0) ∂x∂τ

^{— B(x} o ^,t)q o ^(t)p o ^{(t) -}

t

• 1    f dC (x o ,t,s)

  (2.15)

  
  

• 2    J —at —^{po (s)} ds-

• где C(xo, t, s) = B(xo+1 — s, s)uo(xo +1 — s, s) + B(xo — t + s, s) uo(xo — t + s, s). Из уравнения Вольтерра 2-го рода находим функцию po, а после этого из (2.6) определяем ui(x,t). >

⊳ Доказательство теоремы 2. Предположим, что теорема 2 доказана и найдены функции p(t,T ) и r(t,T ), принадлежащие указанным выше классам. Тогда решение и _ш (x,t) задачи (2.1) согласно теореме 1 удовлетворяет асимптотической формуле (2.3), в которой функции U i , i = 0,1, 2, 3, V j , j = 2, 3, являются единственными решениям соответствующих задач (2.4)–(2.10). Из соотношений (2.3) и (2.11) следуют равенства:

U i (xo ,t)= q i (t),    t E [0,T], i = 0,1, 2, 3;

(2.16)

V k (x o ,t, T ) = X k (t, T ), (t, T ) E Q, k = 1,2.

Таким образом, условия (2.16) являются необходимыми для выполнения асимптотической формулы (2.11). С другой стороны, неизвестные функции p(t, т ) и r(t, т ) однозначно определены именно из соотношений (2.16), причем, как следует из предыдущих рассуждений данного параграфа при этих p , r однозначно определены коэффициенты u i ( x, t ), i = 0,1, 2, 3 и V k (x, t,T ), k = 2, 3, для которых справедлива формула (2.3). Из (2.3) и (2.16) вытекает формула (2.11). ⊲

Замечание 3. Задача о восстановлении функций ρ и r может быть однозначно решена и при несколько меньших требованиях гладкости, налагаемых на функции B , ρ, F и r . Действительно, доказательство теоремы 2, по существу, не изменится, если в теореме 1, на которую оно опирается, порядок малости O(w ^-4 ) (см. формулировку теоремы 1) будет заменен на o ω ^-3 , ω → ∞ . Для доказательства же теоремы 1 в последнем случае требуется меньшая гладкость данных. Отмеченное обстоятельство в данной работе незначительно, поэтому мы остановились на первом варианте, доказательство которого немного короче.