Восстановление донной поверхности по различным картографическим данным

Для построения гидродинамических моделей мелководных водоемов и прибрежных систем требуются точные электронные карты этих объектов [1]. Как правило, обычные бумажные карты являются основным источником информации для построения электронных карт. В данной статье рассмотрен последний этап построения карт, когда различная картографическая информация (отметки высоты, изолинии высоты, области, отмеченные различным цветом) уже переведена в цифровой вид. Предлагаемый метод также подходит для интерполяции других измеренных данных. Основное отличие предлагаемого метода от других методов интерполяции заключается в том, что он может учитывать точность измерений и форму области интерполяции.

Математически задача формулируется как оптимизационная задача с естественными ограничениями. Для получения результата должна быть решена система линейных уравнений с ограничениями. Это требует большого объема вычислений при использовании итерационных методов. Для существенного сокращения объема вычислений использован многомасштабный подход; дополнительное ускорение получено за счет использования параллельных вычислений.

1.    Оптимизационная задача восстановления поверхности

В плоской области G заданы ограничения на диапазон изменения высот: функции т^у^ и М (х^у) такие, что т^у) < М (ху) где (ж, у) Е G — горизонтальные координаты некоторой точки области. Это означает, что значение реальной глубины/высоты е(х,у) в области G удовлетворяет неравенствам т^х^у^ ^ в (ж, у) ^ М (х^у). Допустимы случаи, когда в некоторых точках или подобластях т (х, у) = —оо и/или М (ж, у) = +оо.

Требуется построить в области G функцию / (ж,у), которая имеет непрерывные производные первого порядка и ограниченные производные второго порядка, удовлетворяющую следующим условиям:

т(ж,у) ^ f(x,y) ^ М (х,у),                         (1)

И m²_+Q1 m²₊№)²₊№)²₊₂ W²₍₂₎ \дх ) уду) удх²)   уду²) удхду)         f

(ж, у) EG

где а 0 —параметр, значение которого будет описано ниже.

Постановка задачи имеет следующие отличия по сравнению с классической задачей интерполяции [2]:

• •    исходные данные представлены в интервальном виде: \т (ж, у), М (х, у)] ;

• •    форма области G также берется в расчет; это важно при интерполяции физических величин, существующих только в пределах некоторой области (например, концентрации загрязнений в водоеме).

Перечисленные особенности расширяют область применения предлагаемого интерполяционного метода.

Функции т (ж, у) и М (ж, у) обычно представляют собой результаты измерений. Например, если мы имеем N измерений глубины/высоты (ж^, у^ е_г), 1 ^ г ^ N, то функции т и М могут быть заданы следующим образом:

т(ж,у) =

М(ж,у) =

е^ Де^, —оо, вг + Де», +оо,

если Зг : х_г = ж, yi = у; иначе.

если Зг : ж_г- = ж, yi = у; иначе.

Здесь величины е^ имеют погрешность измерения Де^ > 0. Предполагается, что координаты Жг, уi известны ТОЧНО.

Обсудим постановку задачи. Минимизация суммы квадратов вторых производных в выражении (2) приводит к тому, что поверхность в каждой точке стремится быть «наиболее близкой к плоскости». Член со смешанной производной присутствует для того, чтобы всё выражение (2) было нечувствительно к повороту системы координат.

Минимизация суммы квадратов первых производных дает тенденцию горизонтального положения интерполированной поверхности. Это соответствует минимизации потенциальной энергии земной поверхности. Коэффициент а ^ 0 (обычно достаточно малый) предназначен для настройки этой особенности.

В общем, модель (1), (2) можно понимать как построение «наиболее гладкой» поверхности, соответствующей имеющимся ограничениям.

Лучшим алгоритмом интерполяции точечно заданных данных считается крайгинг [3]. Однако он вычислительно трудоемок и не учитывает форму области интерполяции. Подбор параметра а позволяет значительно приблизить результаты предлагаемого метода к результатам интерполяции, получаемым при помощи крайгинга. По-видимому, в случае точечных исходных данных, имеющих одинаковую погрешность измерения Ае^ = Ае, значение параметра а следует выбирать таким, чтобы кривая

9                    ,             к 2

7 W = g (Ае)² + А • (1 - e^J , h >  О

при некотором параметре к > 0 наиболее близко аппроксимировала экспериментальную вариограмму [3], вычисленную по точкам (ж^у^е^), 1 г 7V.

2.    Дискретизация задачи

В дальнейшем для простоты изложения будем считать, что G — квадратная область: G = ((ж, у) : 0 ^ х ^ Н, 0 ^ у ^ Н). Построим в области G равномерную прямоугольную сетку G, состоящую из N х N квадратных ячеек Су (м = 1, —^N) размерами h = H/N. Далее будем считать, что N ^ 4 и N кратно четырем.

Определим сеточные функции ту и Му:

Му = <

mij = sup т (х, у);

(®»)еС,^

М_г,₃ = , inf М (ж, у);

1х^Сг,3

Mij, (^1,3 + Mij^ /2,

если m_%s3 ^ M^ иначе;

если my ^ M_t)3l иначе.

Тогда дискретные аналоги выражений (1), (2) могут быть записаны следующим образом:

^mid ^ fij ^ Mij? гу ^— 1,...,7V;

(Ю)

• — ^2 52 52     — A-ij) + (Кз— Aj-i) ) +

г=2 з=2

⁺ Д4 52 52 ((A-1J ”2-fy + A+lj)² + Um-1 - 2 fy + fy-^i)²^ + г=2 з=2

2 ^N N

+ У^ 52 (A,j ™ A-1J - Aj-1 + /г-1 J-l) -min, (11)

г=2 j=2

где fl)3 —неизвестные величины. Для сокращения записи будем считать, что fy = 0, если Сг)3 ^ G.

3.    Решение дискретной задачи

В выражении (11) R является функцией аргументов fy^ iy = 1, ...,7V. Если зафиксировать значения всех аргументов функции В, кроме некоторого аргумента fT)Sl то она будет представлять собой многочлен второй степени с положительным коэффициентом при f^ 8. Такая функция обладает минимумом, который достигается в единственной точке /Г)5, определяемой из уравнения:

эн

»S fr,s=fr,s

Тогда минимум функции JR, как аргумента f_T)Sy при ограничениях (10) будет достигаться в точке /*₅, определяемой следующим образом:

/*_$ = max (m_r,_s, min ^M_r,_Sl f_r,^ = L_r,_s (/_r,_s) .                   (14)

Решим уравнение (13). Дифференцируя R no ft^ получим:

уу . “ ^2 t^^-1 * ^o fi--!^ ^+1 * (A+lj fi^ +

+ bj-1 • (/г,J ~ Aj-l) “ bj+1 • (Aj+1 — Aj)] +

+ Д4 [^—262-1^4-1 • (A-lj — 2/^ + A+lj) — 2bj-ij4-i • (Aj-l — ^fij + A,j+1) +

+ bi-2 * Ui-2,3 - 2/i-lj + fi^ + b_W * (Aj - 2A+1J + A+2,j) +

+ b₃_2 • Ui,j~2 - 2Aj-l + fi^ + bj-^2 ^e Uij - 2/ij+l + Aj+2)] + 4

+ д4 IA-l,j-l * U + /г-lj-l) “

“ Ьг+lj-l ’ Ui-Vld ^— fij ^— fi-Vl^-l + fij-Й —

- bi-lj-vi • UkrVl - A-1J+1 ~ /г,j + /г-l,j) +

+ Ьг+lj+l * (/г+lj+l — Aj+1 ~ /г+l,J + Aj)] > (15)

где сомножители b^ и b^^ = b^ • Ь^₂ предназначены для правильной записи выражения (15) в приграничных ячейках:

_ь J 1, если 1 к N-,                               ₍₁₆₎

( 0, иначе.

Найдем значение /г^, при котором частная производная (15) равна нулю:

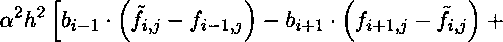
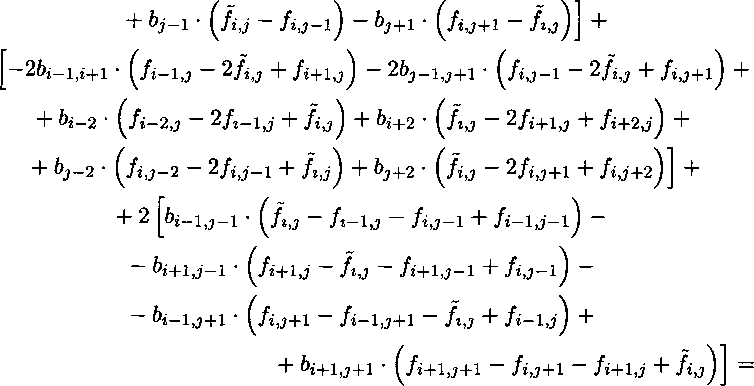
Сгруппируем члены:

fy * [^q2^² (Ьг-1 + Ьг+1 + bj-1 + bj+1) + 4 (bi-i’i-H + bj-lj+l) +

+ (Ьг-2 + Ьг+2 + bj-2 + bj^ + 2 (Ьг-lJ-l + Ьг+lj-l + &i-lj+l + &i+lj+l)] “

- /г—ij • \o?h²bi-i + 26i-i^+i + 2bi-2 + 2^_ij_i + 2bi-ij+i] —

/г+lj * [^ b> Ьг+l + 2Ьг— i,i+l + 2bi+2 + 2&1+1J-1 + 261+1,5+1] — ~ Ji,3—1 ‘ [a² 6² 65-1 + 265—1^4-1 + 2b₃-2 + 261-1,5-1 + 261+1,5-1] —

.            ~ Ji,j+i ' [a²h²65+i + 265-1^+1 + 2Ь_з+2 + 261-1,5+1 + 261+1,5+1] +

+ /г—lj—1 1 261-1,5-1 + /г+i,5-1 • 261+1,5-1 + /i-i,5+1 • 261-1,5+1 + /i+1^+1 • 261+1,5+1 +

+ Ji—2,j " 6i-2 + /i+2J ^- 6i+2 + Ji,3-2 ¹ bj-2 + Ji,3+2 ' bj+2 0. (18)

Введем обозначения:

k^j’⁰ = а² 6² 6i-i + 26i_i,i+i + 261-2 + 261-1,5-1 + 261-1,5+1;

k^j’° = a²6²6i+i + 26i_i,i+i + 261+2 + 261+1,5-1 + 261+1,5+1;

ki’₃¹ c^h^bj-i + 265-1^+1 + 265-2 + 261-1,5-1 + 261+1,5-1;

k^'j^ = o?h²b₃+i + 265-1,5+1 + 265+2 + 26i_i,5+i + 261+1,5+1;

У' ^{1 =}          k^ ¹ = -26i+i,5_i;

7—1>+1      HL       , 7 + 1,+ 1                                               '

У'° = -⁶-« *=™ = -W, с² = -6,-2; к°? = -»,+=;

I? - ?'° + k?° + ^T* + £"’,⁺¹ + i?'"¹ + K'"^Y +

•м ^гД ^гД ^гД ^гД ^гД        ^гД

+ У¹⁺¹ + Щ’⁺‘ + У'° +    + S? + kt?;

ч?=^7С i?+vi<2.

Тогда уравнение (18) может быть записано следующим образом:

Ь°’° . а _ ь~^1>0 .      . _ £⁺¹’° . f л • — ^⁰’^-1 .      1 — £^0,+1 •       —

^гд Ь-Нд кгд   ^Д~^ ку Ьд-¥Х

/          L+lj—1 /          К-1>+1 £          7+1,+1 р кгд *          к1д * Л+lj-l  кгд   * Л-1д-Н \j * A+lj+l

7—2,0 р        7+2,0 р        70,-2 р        70,+2 р

- кгд * Ь-У - ^кгд • Л+2 Д ~ ^кг^ * 1гд-2 ™         j₊₂ = 0,

Кд ⁼ У^ Ц'з * /г^-рд+д = Sy (fi-2₃j-2^   /г-^-2д-^-2) •                 (20)

0<|p+g|^2

С учетом (20) выражение (14) принимает вид:

/r,s ⁼ -^r,s (T)S (/_r_2,5—2? •••? fr +2,s+2)) •                               (21)

Полученный оператор (21) дает оптимальное значение отдельно взятой переменной f_T)S при фиксированных значениях остальных переменных. Используем этот оператор для построения итерационного процесса решения задачи (10), (11).

Итерационный процесс можно осуществить, обходя ячейки сетки построчно, аналогично методу Гаусса—Зейделя. Однако такой алгоритм не подходит для решения на параллельной системе из-за цепной зависимости вычисляемых величин друг от друга. Поэтому обобщим для данной задачи метод верхней релаксации с красно-черным упорядочиванием узлов [4].

Для этого разделим всё множество ячеек сетки на 16 классов в соответствии со следующей
таблицей, имеющей размеры N х N: " 1   13  4   16 9   5  12  8 3  15  2  14 В =    11  7  10  6	1 13 4 ... " 9   5 12 3 15 2 11 7 10 ... •                        (22)
1 13 4 16	1 13 4

Каждая итерация выполняется следующим образом: вначале уточняются (при помощи оператора (21)) значения тех элементов, которые принадлежат первому классу, затем уточняются те элементы, которые принадлежат второму классу, и так далее до класса номер 16. Разностный шаблон оператора S ограничен квадратом 5 х 5, а элементы каждого класса отстоят друг от друга на 3 ячейки сетки, поэтому элементы одного класса будут вычисляться независимо друг от друга. Это позволяет проводить вычисления параллельно.

Часть таблицы (22) размерами 4x4 ячейки называется матрицей Байера [5]. Она широко известна в теории обработки изображений. Существуют подобные матрицы любого размера 2П х 2П. Применительно к задаче итерационного решения системы уравнений особенностью этой матрицы является то, что низкочастотные составляющие ошибки, вносимой выбранным порядком обработки элементов, имеют максимально высокую частоту. Для сравнения, если использовать итерационный метод Гаусса—Зейделя без переупорядочива-ния узлов, получим ненулевую гармонику ошибки с длиной волны, сравнимой с размерами области. Такую гармонику можно трактовать, как появление выделенного направления, вызванного выбранным порядком обхода узлов. Ситуация усугубляется тем, что подобные итерационные методы крайне медленно снижают низкочастотные составляющие матрицы ошибок.

Для формальной записи итерационного метода нам потребуется представление матрицы В, дающее смещение элементов каждого класса по его номеру:

В® = (1,3,1,3,2,4,2,4,1,3,1,3,2,4,2,4)^т;

В« = (1,3,3,1,2,4,4,2,2,4,4,2,1,3,3,1)^г.

Тогда алгоритм итерационного процесса можно записать следующим образом:

Repeat //повторяем итерации d 4- 0 //изменение решения на текущей итерации

For с = 1,..., 16 //перебираем все классы ячеек

For i = В”, В* + 4, ... , В^ + N - 4

For з = В® В® + 4, ... , В® + N — 4 „                   ’     ’ ^с                                            (24)

/   ^ S'ij (/i-2,j-2,—,/i+2j+2)

f ^Li,j (t¹ ~ ^w) ' fi,3 + W • 7) d   <- max (d, |/- fi,₃^

fi,3 7

While d > e.

Здесь Si)3 — оператор минимизации функции (11), определен в выражении (20); В^^—оператор, ограничивающий сеточную функцию в соответствии с (10), определен в выражении (14); и) — релаксационный параметр; (В^,Вп)—смещение элементов класса номер п в сетке; смещения определены в выражении (23); е — некоторое заданное малое число; когда максимальное изменение решения на текущей итерации становится меньше б, итерации останавливаются.

При реализации алгоритма (24) имеет смысл вначале вычислить все возможные варианты оператора S^₃ (таких вариантов 25 штук в случае прямоугольной сетки), и затем использовать нужный оператор в зависимости от взаимного расположения вычисляемой ячейки и границ области.

4.    Свойства задачи и алгоритма

Назовем ограничения (10) невырожденными, если inf М (х, у) < sup т (ж, у).                          (25)

(ж,з/)еС7             (x^eG

Для случая невырожденных ограничений и а > 0 доказаны следующие утверждения:

• 1.    Дискретная задача (10), (11) имеет единственное решение для любого числа ячеек N.

• 2.    Итерационный процесс (24) сходится к решению задачи (10), (11) при 0 < и)< 2 для любого начального приближения.

• 3.    Дополним графики функций т(х,у) и М (х, у) вертикальными поверхностями в местах разрывов, получив поверхности тпМ соответственно. Если т (ж, у) ограничена сверху, М (ж, у) ограничена снизу, и существует такое число е > 0, что минимальное расстояние между поверхностями т и М будет больше е, то решение дискретной задачи (10), (11) поточечно стремится к решению непрерывной задачи (1), (2) при шаге сетки h -> 0: / (ж^, у₃) - f^ = О (h).

5.    Параллельный многомасштабный алгоритм решения 6.    Тестовая задача

Первый порядок точности вызван тем, что сумма (11) не самым лучшим образом аппроксимирует выражение (2) на границах области G. Повышение порядка аппроксимации усложнит алгоритм, но не даст практической пользы, так как значения сеточной функции, вычисляемые между заданными точками, почти не зависят от значений вблизи границ области.

Как уже было сказано выше, итерационный метод (24) очень медленно снижает низкочастотные гармоники матрицы ошибок. В частности, если расстояния между точками с известными значениями функции велики по сравнению с размером ячеек, то число итераций может иметь порядок О ^N²y Кроме того, при использовании чисел одинарной точности итерационный процесс может не сойтись к правильному решению из-за накапливающихся ошибок округления.

Самый эффективный метод решения этих проблем — использование многомасштабного алгоритма, который легко реализуется в данной задаче.

Предположим, что N = 2^. Сделаем уменьшенную вдвое копию сетки, объединив ячейки по 4 штуки. При объединении ячеек из четырех ограничений сверху выбирается минимальное (см. (8), (9)), а из четырех ограничений снизу — максимальное. Если ограничение сверху оказалось меньше ограничения снизу, то оба ограничения заменяются на их среднее арифметическое. Полученную сетку можно снова уменьшить вдвое и так далее, пока не дойдем до сетки размерами 4x4 ячейки. Решим задачу на этой сетке при помощи алгоритма (24), и используем полученное решение в качестве начального приближения для решения на сетке 8 х 8. При переносе значений с грубой сетки на подробную достаточно использовать простейшую билинейную интерполяцию (центры ячеек грубой сетки не совпадают с центрами ячеек более подробной сетки). При решении задачи на различных сетках нужно учитывать, что оператор 8-ц зависит от шага сетки при а ^ 0. В конце концов доберемся до исходной самой подробной сетки, для которой будет хорошее начальное приближение, полученное с более грубой сетки.

Параллельный алгоритм проще всего реализовать для вычислительной системы с общей памятью. В этом случае не требуется пересылка данных. Вычисления всех элементов одного класса являются независимыми операциями. Это означает, что в алгоритме (24) можно разделять циклы по г и по j как угодно между процессорами. Самый простой и эффективный способ — это разделить цикл по индексу г на равные части соответственно числу процессоров/ядер процессора.

В качестве примера рассмотрим задачу интерполяции данных, показанных на рисунке 1. Прежде всего, следует отметить, что метод не требует распознавания изолиний глубины: в качестве входных данных может быть использован цвет областей, поэтому достаточно закрасить области между изолиниями различными цветами. Каждый цвет обозначает свой диапазон глубин, который записывается в ограничения по высоте при построении сетки.

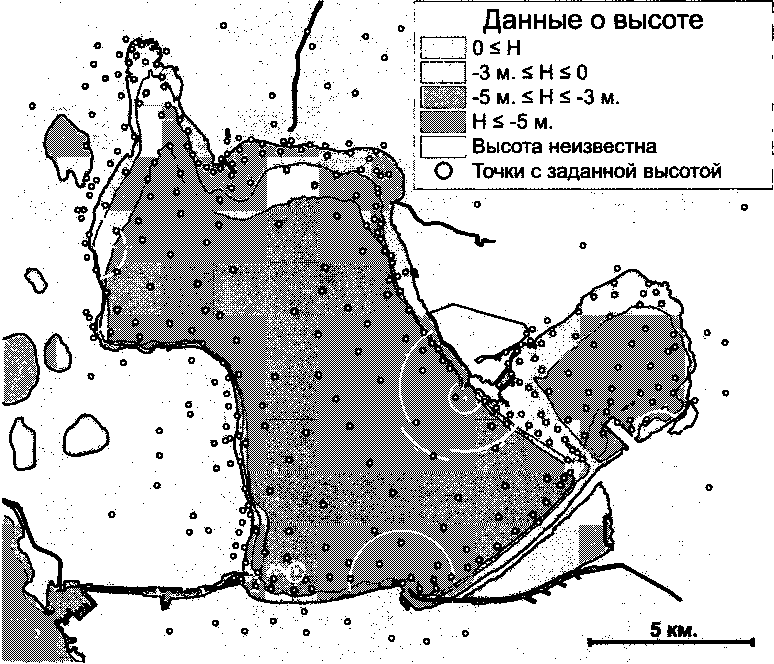
Рис. 1. Пример данных о высоте для озера Этанг-де-Берр (Франция)

Кроме областей с цветом карта имела множество отметок глубины и высоты (на рисунке 1 показаны кружочками), которые были оцифрованы и внесены в соответствующие ячейки сетки при ее построении. Погрешность всех данных внутри водоема положена равной 0,1 метра, погрешность данных за пределами водоема —1,0 метр.

Кроме того, была отдельная карта для маленького треугольного водоема на юго-востоке карты (Этанг-де-Больмон). Ее данные не показаны.

Для вычислений использовалась сетка размерами 512 х 512 ячеек. Значение параметра а = 3 • 10“³ 1/м. Сеточные величины — числа двойной точности. В качестве критерия сходимости итерационного процесса была выбрана величина 6 = 0,001 метра. Процессор тестовой системы: Intel Core 2 Quad 2,4 GHz, 8 MB L2 Cache.

Вначале был произведен расчет последовательным одномасштабным алгоритмом. Потребовалось более 50 тысяч итераций (14 минут машинного времени) для того, чтобы итерации сошлись.

Затем был произведен расчет многомасштабным алгоритмом. На сетке каждого масштаба требовалось произвести от 10 до 100 итераций. В итоге алгоритм сошелся за 215 итераций (2,9 секунд машинного времени). Использование многомасштабного алгоритма позволило ускорить вычисления в 300 раз!

После этого была реализована параллельная версия программы при помощи ОрепМР. При запуске с двумя вычислительными потоками программа справилась с задачей интерполяции за 1,6 секунды (эффективность 90%). При запуске с четырьмя потоками интерполяция завершилась за 0,9 секунды (эффективность 81%).

Время чтения исходных данных и построения по ним сетки (вычисления ограничений) на всех тестах составляло около пяти секунд и не принималось во внимание.

Результат интерполяции показан на рис. 2. Изолинии высоты за пределами водоема не показаны, так как данные о высоте на исходных картах практически отсутствовали.

Рис. 2. Результат интерполяции. Масштаб указан в метрах

7.    Заключение

Представленный алгоритм интерполяции может быть эффективно применен для объединения и интерполяции исходных данных различного типа. Кроме того, алгоритм учитывает возможную погрешность исходных данных, что позволяет уменьшить шум и более правильно объединить данные из различных источников.

Дискретизация задачи может быть проведена в области любой формы (не только квадратной, как описано в статье) и на различных сетках (в том числе на треугольной сетке). Учет формы области позволяет более правильно произвести интерполяцию величин, которые распределены только в пределах заданной области.

Реализация программы с использованием многомасштабных алгоритмов и распараллеливание ее с использованием нескольких вычислительных потоков позволяет получать результаты за разумное время на персональном компьютере.

Планируется усовершенствование метода путем введения в модель горизонтальной погрешности исходных данных (в дополнение к вертикальной) и нежестких ограничений на функцию: математическое ожидание и дисперсия вместо минимального и максимального допустимых значений.

Статья рекомендована к печати программным комитетом международной научной конференции ^Параллельные вычислительные технологии 2009 >.