Восстановление фона в областях кадра с объектами малого размера в видеопоследовательности

В связи с развитием вычислительной техники становится актуальной задача реконструкции видеопоследовательностей: восстановление оригинального изображения под искусственно наложенными графическими объектами (логотипами телевизионных каналов, субтитрами и т. д.), удаление следов повреждения носителя информации (царапины на кинопленке и т. д.) и других объектов малого размера (изображений на некотором фоне человека, дерева, камня и т. п.). Решение данной задачи в общем виде приведет к снижению затрат на повторное использование видеоматериалов, под которым понимается ремастеринг старых фильмов, ретрансляция материала различными телевизионными каналами с удалением ранее наложенных, но уже неактуальных изображений компьютерной графики, а также случайно попавших в кадр объектов, например, рекламных конструкций.

Наложенные изображения компьютерной графики, встречающиеся в видеоматериалах, можно разделить на следующие виды: телевизионные логотипы – изображения небольшого размера, как правило, размещенные в одном или нескольких углах кадра или у границ кадра; титры – текстовые области с информацией о создателях фильма, могут быть размещены в любом месте кадра; субтитры – текстовые области у верхней или нижней границ кадра с периодически изменяющимся статическим текстом; бегущая строка – текстовая область у верхней или нижней границ кадра с перемещающимся текстом, перемещение текста осуществляется в соответствии с общепринятыми правилами чтения и письма.

Все разнообразие накладываемых изображений компьютерной графики можно классифицировать по различным признакам. Приведем наиболее часто встречающиеся: по размеру: маленькие (до 5 % экрана), средние (до 20 % экрана), большие (до 35 % экрана); по местоположению: угловые, вытянутые по горизонтальной границе кадра, вытянутые по вертикальной границе кадра, в соответствии со стандартом Substation Alpha или иное; по динамике: статические (изображение всегда постоянно), умеренно изменяющиеся (изображение без изменения размеров), полностью динамические (изображение изменяет размеры, в пределах этих размеров может быть наложена другая видеопоследовательность); по длительности: постоянные на всей видеопоследовательности, периодически отсутствующие; по цветности: однотонные, черно-белые, градиентные, с ограниченным количеством цветов, пол- ноцветные; по прозрачности: прозрачные и непрозрачные; по наличию контурных линий: обрамленные, без обрамления; по наличию собственного фона: с наличием собственного фона, не обладающие собственным фоном [1].

Искажения изображения вследствие повреждения носи- теля чаще всего имеют протяженную геометрическую структуру, могут возникать на любом месте кадра и иметь различные углы наклона. Характерной чертой поведения искажений во времени является их присутствие на нескольких после- довательных кадрах, никак не связанное с изменением ракурса сцены. На видеопоследовательности могут присутствовать несколько таких структур, причем каждая из них характеризуется собственным поведением и может перекрывать другие структуры. Неопределенность и непредсказуемость появления повреждений делает поставленную задачу достаточно сложной для автоматической реализации. Только гипотеза о протяженности геометрической структуры, ее малой площади относительно всего кадра, однородной яркости и стабильности существования в течение последовательности кадров позволяет разработать метод локализации таких структур и реконструкции первоначального изображения.

Случайно снятые и ненужные в кадре объекты должны характеризоваться малым размером (до 10 % размера кадра), а также статическим положением на динамическом фоне; динамическим положением на статическом фоне; динамическим положением на динамическом фоне.

Правильная классификация удаляемых объектов позволит выбрать комплекс алгоритмов для проведения восстановления первоначальной видеопоследовательности. Для общего случая порядок восстановления оригинальной видеопоследовательности представлен ниже с подробным рассмотрением каждого шага.

Шаг 1 . Определение характеристик видеопоследовательности (особенных точек кадра, векторов движения в кадре, движения объектов и текстур в кадре).

Одной из технологий извлечения структурированной и осмысленной информации из видеопоследовательности является слежение за точечными особенностями изоб- ражений видеопоследовательности. Под точечной особенностью понимается такая точка сцены, которая находится на плоском участке поверхности сцены. При этом изображение окрестности этой точки можно отличить от изображений окрестностей всех других точек сцены из некоторой другой окрестности этой точки.

Чаще всего для отслеживания точечных особенностей изображения (кадра) используется детектор Харриса, в котором для каждого пиксела изображения вычисляется значение особой функции отклика угла, оценивающей степень похожести изображения окрестности точ- ки на угол. Для этого рассчитывается матрица

M =

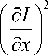
a i Ya/ a x Да y

a I Ya / a x Да y

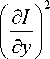
где I ( x , y ) – яркость изображения в точке с координатами ( x , y ).

В случае когда оба собственных значения матрицы велики, даже небольшое смещение точки ( x , y ) вызывает значительные изменения в яркости, что и соответствует особенности изображения, и функция отклика угла записывается в следующем виде:

R = det M - k(trace (M))2, где k = 0,04 (коэффициент, предложенный Харрисом); trace(M) – функция расчета суммы элементов матрицы на главной диагонали.

Точки изображения, соответствующие локальным максимумам функции отклика угла, и признаются особенностями.

Рассмотрим простую схему детектора точечных особенностей [2].

• 1.    Детектирование и оценка.

  • 1.1.    Нахождение набора особенностей {F}, исходя из характеристик особенности – степени экстремальности функции отклика угла, местоположения особенности (в центре изображения, у границ изображения, у углов изображения), местоположения особенности относительно других особенностей или плотности особенностей в некоторой области кадра.

  • 1.2.    Определение качества всех особенностей – Q {F}. Наиболее качественными особенностями считаются особенности с большей степенью экстремальности функции отклика угла, достаточно удаленные от границ кадра, с низкой плотностью особенностей в интересующей нас области кадра. Для оценки качества могут быть использованы методы многоатрибутивного принятия решений, например метод упорядоченного предпочтения через сходство с идеальным решением.

  • 1.3.    Выбор особенностей, чье качество выше некоторого заранее или динамически определяемого порога, и формирование множества{G}.

• 2.    Слежение и оценка.

• 2.1.    Нахождение в текущем кадре нового положения всех особенностей из {G} – слежение.

• 2.2.    Определение текущего качества всех элементов множества{G}.

• 2.3.    Выбор только тех особенностей, чье качество удовлетворяет некоторому критерию. Как правило, таким критерием служит интегральный критерий или степень экстремальности функции отклика угла.

• 2.4.    Если число отслеживаемых точек уменьшается ниже требуемого уровня, то осуществляется применение детектора к текущему изображению и добавление в множество {G} новых точек.

Для каждого последующего кадра:

Для отслеживания изменения координат точечных особенностей применяются модификации алгоритма Лука-са–Канаде [3]. Последней модификацией алгоритма Лука-са–Канаде является алгоритм Джин–Фаваро–Соатто, учитывающий смещение особенностей, аффинные искажения особенностей, аффинные изменения освещенности особенностей. Задача слежения за особенностью сводится к определению параметров движения и искажения окна особенности, при которой минимизируется разность с = J J (J (Ax + d)-1 (x))2 w(x)dx,

W где W- окно особенности; w(x) - весовая функция (может быть равна единице во всем окне); J(x) и I(x) - два изображения; Ax+d - смещение точки.

Выражение дифференцируется относительно параметров движения, и производная приравнивается к нулю. Затем система линеаризуется с помощью разложения функции изображения в ряд Тейлора:

J ( Ax + d ) = J ( x ) + g ^T ( u ).

Это дает нам линейную систему из шести уравнений с шестью неизвестными

Tz = a , где в векторе z объединены все искомые параметры: z ^T = Г d   d d d d d ].

L xx yx xy yy x y -I

Вектор ошибки a записывается в виде a=JJ

W

xg xg yg yg

x

x

wdx ,

g

g

x

y

а матрицу T можно представить следующим образом:

U

V ^T

V

Z

U =

^T = JJ

W L

2 „2

x gx x 2 gxg xygx xygxg

x ² gxg;

2 _2

x gy xygxg xygy

wdx

xygx xygxg

2 _2

У g x

У ² g x g.

V ^T

xgx2

xgxg

Z =

xgxg xgy gx gxgy xygxg xygy У 2 gxg.

2 _2

У g y

y yg2

yg2

ygxg

g_xg g y

Полученная система решается также итеративно по методу Ньютона-Рафсона.

Если движение считается не аффинным, а просто смещением, то первые четыре элемента искомого вектора z обращаются в ноль, и значимыми остаются только последние два. Алгоритм превращается в алгоритм Томаси-Канаде.

Дополним приведенный алгоритм для случая переменного освещения.

Пусть поверхность сцены, на которой найдена особенность сцены, является ламбертовой. Тогда интенсивность освещения точки определится формулой x = P ( X), где X - точка сцены; P - оператор проектирования; x -точка на изображении, может быть описана как

I ( x ,0) = v_EE ( X ) + ^ e V x е W u , где E ( X ) - альбедо (отражающая способность) точки сцены; U - окрестность точки сцены; v и E - постоянные параметры, которые представляют изменения контраста и яркости изображения соответственно. При движении камеры эти параметры меняются, т. е. зависят от времени. Изменения освещенности во времени можно записать как

I ( x , 0) = v ( t ) I ( x , t ) + Z ( t ) V x e W u , где

v ( t ) = v' ¹ ' , Z ( t ) =^ ( t ) - v' ¹ ' ^ (0) ,           ~E                E

V e ⁽ t )                     V e ⁽ t )

при t > 0. Объединив аффинное движение окрестности особенности с изменением освещенности, получим выражение

I ( x , 0) = v ( t ) I ( Ax + d , t ) + Z ( t ) V _X e W .

Из-за шума в изображении, а также из-за приближенного моделирования движения и изменения освещенности это уравнение в реальности никогда не будет выполняться, поэтому задача слежения состоит в минимизации разности между окрестностями текущего и нового положения особенности:

c = J (I(x, 0) - vI(Ax + d, t) + Z)2 w(x)dx, где w(x) - весовая функция. С помощью разложения в ряд Тейлора в окрестности d = 0, v = 1, Z = 0 получим vI(y, t) + Z ~ vI(x, t) + Z + VI |y (u - u0), d u y = Ax + d A = {dj};

A = { d_ti } ;

d = [ d 1 d ₂ ] T ;

u = [ d ii d ,2 d 2, d 22 d i d 2 ] ;

u₀ = [ 1 0 0 1 0 0 ] .

Переписав получившееся равенство в матричной форме, получим следующее уравнение:

I (x ,0) = F (x, t) T z, где

• F ( x , t ) = L xI x yI x yI y I x I y I i ] ;

z = [ d ,, d ₁₂ d ₂₁ d ₂₂ d , d ₂ u Z ] T •

Домножив на F ( x , t ) T и проинтегрировав по всему окну особенности W с весовой функцией w , получим систему из восьми уравнений с восемью неизвестными:

Sz = a ;

a = J F ( x , t ) T I ( x ,0) w ( x ) dx ;

W

S = J F ( x , t ) T F ( x , t ) w ( x ) dx .

Заменив интег р ирование на сумму по всем пикселям в окне W , мы приходим к следующей системе линейных уравнений:

Sz = a

	Г x 2 I* xyI x	S xyI2 ; y 2 I x	= Z x e W x 2 1 xyI	■ T U T xIy xIy	U " V _ xyIx y 2 I x	I y I y	xI x yI x	xI x I y ' yI x I y
T =	x 2 I x I y	xyIxIy	x 2	I y	xyI y		xIxIy	«I ;
	xyI x I y	y 2 I x I y	xy	I y	y 2 1	2 y	yIxIy	yI y
	xI x	yIxIy	xIx	I y	yIxIy		I x	u,
	_ xIx I y	yI 2	xI	2 y	yI	2 y	I x I y	i ;

U T =	xI x I xI, x	yI x I yIx	xIyI yIyI xI y     yI y		I x I I x	I y I I y
			\ 1 2 ' 1
		V =	[ I 1 J

Если матрица S получается обратимой, то решение системы линейных уравнений можно записать в виде z = S-1 a.

Как во всех алгоритмах слежения, система решается итеративно по методу Ньютона–Рафсона. Итерации происходят до тех пор, пока изменения решения не становятся пренебрежимо малы.

Шаг 2 . Разделение видеопоследовательности на сцены.

Для повышения качества восстановления необходимо разделить видеопоследовательности на сцены по следующему алгоритму.

• 1.    Расчет расстояния от каждой особенной точки кадра до центральной точки кадра по формуле

• 2.    Расчет смещения точки по формуле

• 3.    Расчет количества сильно смещенных точек в j -м кадре по формуле

Rj = J(xG, - xc )2 + (yG, - yc )2 , где xGi,yGi – координаты i-й особенной точки; xc, yc– координаты центральной точки кадра.

| Ry - Ry -i| < e, где e – порог смещения точки для кадра.

f (R, e, j) = count(e > en), где en – общий порог смещения. Если на текущем кадре j функция f достигает локального максимума, то текущий и последующий кадр являются границами сцены видеопоследовательности. Качество определения границы сце- ны можно описать следующими параметрами:

– точностью, представляющей собой вероятность, что найденная граница сцены верна:

P =

C

C + F ’

– граничным сигналом, являющимся вероятностью того, что ожидаемая граница сцены будет найдена

V = -C- ;

C + M

– синтетической мерой точности на основе точности и граничного сигнала:

F 1 =

2 PV

P + V

где С – количество верных срабатываний; М – количество пропущенных сцен; F – количество ложных срабатываний.

Шаг 3 . Определение типа сцены (с движением, без движения).

Если на этапе отслеживания особых точек кадра видеопоследовательности удается определить вектора движения точек в кадре, будем считать, что эта видеопоследовательность и сцена как ее часть обладает движением. Исходя из этого, на этапе восстановления первоначальной видеопоследовательности будем использовать пространственновременной алгоритм получения информации из соседнего кадра. В том случае когда на этапе отслеживания особых точек не удается определить вектора движения, будем счи- тать, что эта сцена не обладает движением, и использовать пространственный алгоритм восстановления на основе информации из областей, находящихся рядом с областями, которые необходимо восстановить.

Шаг 4 . Определение границ областей наложенных изображений компьютерной графики в случае восстановления видеопоследовательности такого вида.

Локализация текстовых областей с искусственно наложенной графикой основана на модификации пространственного алгоритма Рареса–Рейндерса–Бьемонда [4]. Данный алгоритм построен на принципе обнаружении областей экстремальной яркости на основе мягкого и жесткого динамических порогов. Для обнаружения области экстремальной яркости мы должны установить некоторые пороги для поиска/локализации ярких и тусклых пикселов. Однако использование фиксированных порогов нежелательно, поскольку яркость меняется от кадра к кадру. Жесткий порог является хорошим решением для обнаружения таких областей, в то время как мягкий порог приведет к большому количеству ложно обнаруженных областей. Чтобы избежать этих проблем, в алгоритме обнаружения областей экстремальной яркости используется динамический порог, который работает для нашего случая весьма эффективно. Основная идея выбора динамического порога состоит в том, что сначала устанавливается жесткий порог, после чего определяются только те области, значения яркости у которых выше начального порога. Области, полученные на этом шаге, расширяются соседними, удовлетворяющими значениям мягкого порога.

Шаг 5 . Определение характеристик восстанавливаемых областей, выбор комплекса алгоритмов для процесса восстановления.

Для видеопоследовательности с признаками движения в кадре анализируется структура нескольких предыдущих кадров видеопоследовательности и изменение полученной структуры предыдущих кадров по сравнению с редактируемым кадром. На основе полученных данных принимается решение об модификации текущего кадра с использованием информации, взятой из предыдущих кадров с учетом изменения структуры кадра.

Для видеопоследовательности без признаков движения в кадре анализируется текстура соседних с восстанавливаемой областью областей, после чего определяется структура и вероятность ее изменения. Хорошим вариантом может быть анализ области текстуры с помощью окна с динамическими размерами и сравнение элементов изображения на границах этого окна. Можно предположить, что при совпадении основных элементов изображения на границах этого окна, изображение внутри окна является желаемым текстоном, и на основе этого изображения допустимо генерировать текстуру для заливки области удаляемого объекта. С учетом полученных данных производится заполнение восстанавливаемой области.

Для сцены видеопоследовательности с признаками движения будем предполагать, что местоположение в виде декартовых координат относительно верхнего левого угла кадра (x1a, y1a, x2a, y2a) и линейные размеры (dx = x2a – x1a; dy = y2a – y1a) реконструируемой области нам известны, кадр в целом движется в одном направлении, характер движения – равномерный и прямолиней- ный. После окончания работы алгоритмов семейства Лукаса–Канаде мы знаем для каждого кадра положение набора точечных особенностей Gi, предыдущее положение набораточечных особенностей Gi–1 в одном из предыдущих кадров и вектор (xv, yv) или направление и величину движения каждой особенной точки между парой смежных кадров. Обладая этой информацией, мы получаем возможность вычислить номер кадра относительно текущего, из которого будет браться информация для восстановления. Приведем описание работы такого алгоритма.

Реконструируемая область в общем случае может иметь прямоугольный вид, поэтому номер кадра n определяем как минимальный – такой, где точка уже находится за пределами области реконструкции n = min(dx/xv; dy/yv), при этом смещение точки замены относительно i-го кадра будет x-n = n ■ xv; y-n = n ■ yv, а координаты x . y‘

x i - n . У1-n

x i - n ■ x_v

У1 ^{- n} ■ У х,

где – текущий кадр; n – смещение кадра, I – n – предыдущий кадр, содержащий информацию для реконструкции; [x , y ] – реконструируемая точка, [x ’, y ’] – реконструированная точка, значение по координатам содержит цвет; [x –n, y –n] – точка на предыдущем кадре, используемая для реконструкции.

Процесс реконструкции повторяем для каждой точки реконструируемой области для каждого кадра сцены, чтобы восстановить полную сцену видеопоследовательности. Мы можем использовать уже реконструирован- ные точки для восстановления других точек того же самого кадра, или уже реконструированные кадры для восстановления прочих кадров реконструируемой сцены.

Данный алгоритм применим для реконструкции областей любых объектов переднего плана, однако накладываются ограничения на размер и местоположение реконструируемой области – в случае если область не лежит на границе кадра, то она может занимать до 90 % линейного размера кадра по своей большей стороне при меньшей стороне до 10 %. В случае если область лежит у одной из границ кадра, то длина стороны реконструируемой области не может быть более 10 % длины границы кадра.

Для сцены видеопоследовательности без признаков движения для восстановления областей кадра небольших размеров можно использовать модифицированный алгоритм, предложенный Ж. Понсом и Д. А. Форсайтом [5]:

• 1.    Выбрать текстурный фрагмент в требуемой локализованной области, исходя из гипотезы о продолжении

• 2.    В цикле вставить текстурный фрагмент в восстанавливаемую область изображения (пока восстанавливаемая область не будет заполнена):

• 3.    В цикле, пока не будут подобраны значения для всех точек на границах синтезируемой области:

текстуры данного вида в восстанавливаемой области.

• – подобрать окружение этого положения по примеру изображения, игнорируя при вычислении оценки схожести положения с неопределенными значениями;

  – выбрать случайным равновероятным образом значение для этого положения из набора значений соответствующих положений подобранных окружений.

• 4.    Конец цикла п. 3.

• 5.    Конец цикла п. 2.

Этот алгоритм имеет большую вычислительную сложность и высокую зависимость от случайных значений. К его достоинствам можно отнести решение задачи заливки текстурой областей с неопределенной формой и стыковки сгенерированного и исходного изображения. Результаты применения алгоритма можно улучшить, используя медианный фильтр.

Итогом работы комплекса алгоритмов должно быть восстановление оригинальной видеопоследовательности, однако основной недостаток заключается в том, что качество работы можно оценить только субъективно или с помощью экспертов.