Восстановление ориентационной функции распределения частиц

Свойства многих искусственных и природных материалов, таких, как растянутые полимеры, жидкие кристаллы, пленки Ленгмюра-Блоджетт, синтетические и биологические мембраны и так далее, определяются ориентационной упорядоченностью молекул. Экспериментальное определение ориентационного распределения частиц в таких частично упорядоченных системах является важной проблемой современной физической химии.

Восстановление ориентационной функции

Наиболее точной характеристикой упорядоченности молекул является ориентационная функция распределения р(а,в, y ) , которая показывает долю частиц, ориентированных в угловом интервале а + da, в + de, Y + dY (а, в, Y —углы Эйлера, связывающие систему координат отдельной частицы с системой координат образца). Одним из эффективных методов определять ориентационную функцию распределения частично ориентированных молекул является метод ЭПР. Положение резонансного сигнала каждой парамагнитной частицы в спектре ЭПР зависит от ориентации этой частицы относительно вектора напряжҷнности магнитного поля.

Таким образом, из спектров ЭПР может быть получена более детальная информация об ориентационном распределении парамагнитных частиц. В связи с этим, актуальной задачей является разработка метода анализа спектров ЭПР анизотропного образца с целью определения ориентационной функции распределения парамагнитных частиц.

Постановка задачи

Интенсивность резонансного сигнала в каждой точке спектра определяется следующим образом:

2 π π    2 π

0  00

F(H, g, A, h) p(a, в, Y) sine da de dY •

Углы Θ и α фиксированы. Поэтому достаточно решить интегральное уравнение

I (н,Ф)

2 π    2 π

F(H, g, A, h) р(в, Y) sine de dY ,

Углы Θ и ϕ определяют положение вектора напряжҷнности магнитного поля в системе координат, связанной с образцом (X ‘ Y ‘ Z ‘ ) (0 — угол между H и осью Z ‘ , у —угол между проекцией H на плоскость (X ‘ Y ‘ ) и осью Y ‘ ).

Углы Эйлера а, в и y связывают систему координат образца (X ‘ Y ‘ Z ‘ ) с системой координат отдельной парамагнитной частицы (X ‘‘ Y ‘‘ Z ‘‘ ).

Задача является некорректно поставленной задачей ( см. [1]).

Способ решения

В данном случае (см. [2]) при решении интегрального уравнения (1) возникает необходимость минимизировать регуляризирующий функционал Тихонова

M ^а [р] = / / dH d^ f / / F(H,^e,Y ) Р(в, y ) sine de dY — I (H, Ф)! + aQ, H 1 ϕ 1               0 0

конечно-разностная аппроксимация которого принимает следующий вид:

N H ^N ϕ

M ^a [p]= EE h H h ^

k =1 l =1

Nβ Nγ hβ hγ Fklij ρij sinβi i=1 j=1

^— I kl  ^{+ aQ},

где P ij = p(e i ,Y j ), I kl = I(H k , ^ l ) , F klij = F(H,V l ,e i ,Y j )—сетка по H,^,e,Y с шагом h H , h ϕ , h β , h γ , числом узлов сетки N H , N ϕ , N β , N γ ,

N H ^N ϕ

^Ф[Р^] = EE h H ^h v k =1 l =1

N β N γ

EE h β h γ F klij ρ ij sinβ i - I kl i =1 j =1

При минимизации функционала Тихонова необходимо вычислять его градиент (см. [3]), который имеет вид:

M ^a [p] =

dM ^a [p ij ]

∂ρ ij

^N H ^{N ϕ}

= 2h e hY^ Y>h _v F klij

k =1 l =1

N β N γ

p =1 q =1

h β h γ F klpq ρ pq sinβ i ^- I kl

dQ(p ij )

+ a о •

∂ρ ij

Идея распараллеливания

При решении данной задачи почти все время уходит на вычисление функционала Тихонова и его градиента. Основной вклад во время вычисления функционала Тихонова вносит невязка (2). Время вычисления стабилизатора пренебрежимо мало. Из формулы (2) видно, что невязка состоит из несвязных между собой групп слагаемых (по k и l).

Это дает возможность применения многопроцессорной системы. Задачу можно распараллелить, т.е. переписать программу таким образом, чтобы независимые части программы выполнялись на разных процессорах (см. [4]). Общая теория распараллеливания приводится на рисунке 1.

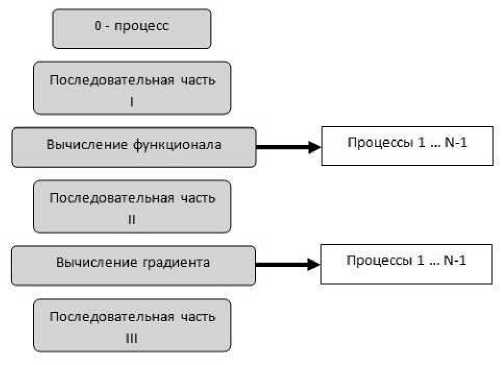
Рис. 1 . Распараллеливание

Экспериментальные задачи были связаны с определением ориентации частиц в образце аксиальной симметрии. Ориентационная функция в этом случае представляет собой распределение оси симметрии образца O в системе координат, связанной с парамагнитной частицей. Углы α, β и γ выбираются таким образом, чтобы β и γ определяли положение оси симметрии образца в системе координат частицы (β — угол между O и осью Z ^′′ , γ — угол между проекцией O на плоскость (X ^′′ Y ^′′ )и осью Y ^′′ ).

FHH, hr)

- /Z2Z   . 2H2

= ynhrexp( hr),

^FЛ^(H, ^hЛ⁾ =

Va

hЛ

2n H ² + 32^"

4 h _Л

Форма линии может быть задана в виде функции Гаусса (3)или Лоренца (4), а также с помощью свҷртки этих функций.

В приведенных формулах центры линий находятся в точке H = 0. Ширина линии, как Гаусса, так и Лоренца, является тензором второго ранга.

Основные результаты

Совместно с сотрудниками Химического факультета МГУ была написана программа, выполняющая численный расчет спектра ЭПР для заданной функции распределения.

На рисунке 2 приведен экспериментально полученный спектр ЭПР. Различные кривые соответствуют разным углам поворота ϕ, который задает положение образца, относительно внешнего магнитного поля H .

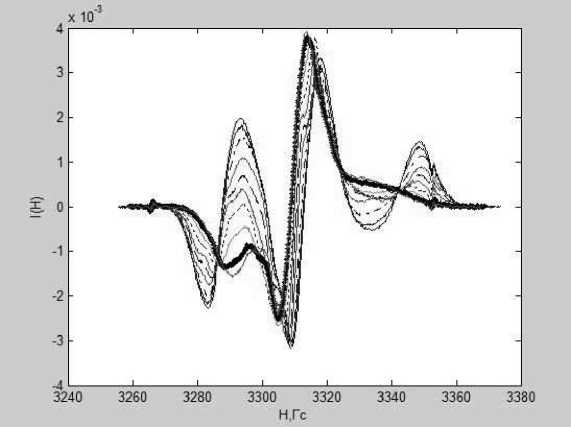
Рис. 2 . Экспериментально полученный спектр ЭПР

Была написана программа решения двумерного интегрального уравнения Фредгольма первого рода, для линейного случая. Программа написана на языке Fortran 90, с использованием функций MPI. Решение задачи осуществлялось на кластерах НИВЦ МГУ и ЮУрГУ.

Работа проводилась при финансовой поддержке гранта РФФИ є 11-01-00040